Доброго времени суток каждому жителю Хабрвилля! Давненько я не писал статей! Пора это исправить!

В сегодняшней статье поговорим о насущной для многих выпускников школ теме - ЕГЭ. Да-да-да! Я знаю, что Хабр - это сообщество разработчиков, а не начинающих айтишников, но сейчас ребятам как никогда нужна поддержка именно сообщества. Ребят опять посадили на дистант. Пока не ясно на какой период, но уже сейчас можно сказать, что ЕГЭ по информатике будет на компьютерах и его можно зарешать при помощи языка Python.

Вот я и подумал, чтобы не получилось как в песне, стоит этим заняться. Я расскажу про все задачи первой части и их решения на примере демо варианта ЕГЭ за октябрь.

Всех желающих - приглашаю ниже!

Быстрый перевод из системы в систему

В Python есть интересные функции bin(), oct() и hex(). Работают данные функции очень просто:

bin(156) #Выводит '0b10011100'
oct(156) #Выводит '0o234'
hex(156) #Выводит '0x9c'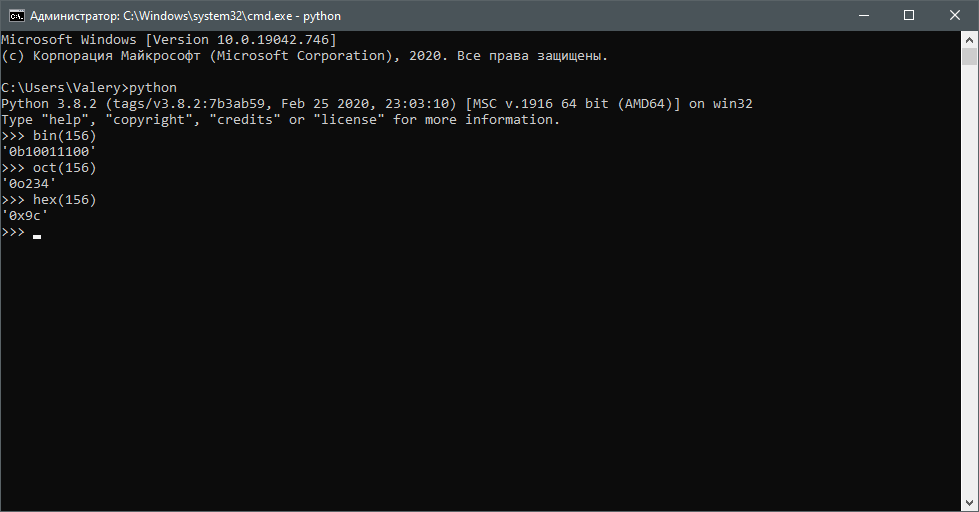

Как вы видите, выводится строка, где 0b - означает, что число далее в двоичной системе счисления, 0o - в восьмеричной, а 0x - в шестнадцатеричной. Но это стандартные системы, а есть и необычные...

Давайте посмотрим и на них:

n = int(input()) #Вводим целое число
 
b = '' #Формируем пустую строку
 
while n > 0: #Пока число не ноль
    b = str(n % 2) + b #Остатот от деления нужной системы (в нашем сл записываем слева
    n = n // 2 #Целочисленное деление
 
print(b) #Вывод

Данная программа будет работать при переводе из десятичной системы счисления в любую до 9, так как у нас нет букв. Давайте добавим буквы:

n = int(input()) #Вводим целое число

b = '' #Формируем пустую строку

while n > 0: #Пока число не ноль
	if (n % 21) > 9: #Если остаток от деления больше 9...
		if n % 21 == 10: #... и равен 10...
			b = 'A' + b #... запишем слева A
		elif n % 21 == 11:#... и равен 11...
			b = 'B' + b#... запишем слева B

'''

И так далее, пока не дойдём до системы счисления -1 (я переводил в 21-ную систему и шёл до 20)

'''

		elif n % 21 == 11:
			b = 'B' + b
		elif n % 21 == 12:
			b = 'C' + b
		elif n % 21 == 13:
			b = 'D' + b
		elif n % 21 == 14:
			b = 'E' + b
		elif n % 21 == 15:
			b = 'F' + b
		elif n % 21 == 16:
			b = 'G' + b
		elif n % 21 == 17:
			b = 'H' + b
		elif n % 21 == 18:
			b = 'I' + b
		elif n % 21 == 19:
			b = 'J' + b
		elif n % 21 == 20:
			b = 'K' + b
	else: #Иначе (остаток меньше 10)
		b = str(n % 21) + b #Остатот от деления записываем слева
	n = n // 21 #Целочисленное деление

print(b) #Вывод

Способ объёмен, но понятен. Теперь давайте используем тот же функцию перевода из любой системы счисления в любую:

def convert_base(num, to_base=10, from_base=10):
    # Перевод в десятичную систему
    if isinstance(num, str): # Если число - строка, то ...
        n = int(num, from_base) # ... переводим его в нужную систему счисления
    else: # Если же ввели число, то ...
        n = int(num) # ... просто воспринять его как число
    # Перевод десятичной в 'to_base' систему
    alphabet = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ" # Берём алфавит
    if n < to_base: # Если число меньше системы счисления в которую переводить...
        return alphabet[n] # ... вернуть значения номера в алфавите (остаток от деления)
    else: # Иначе...
        return convert_base(n // to_base, to_base) + alphabet[n % to_base] # ... рекурсивно обратиться к функии нахождения остатка

Вызвав функцию вывода print(convert_base(156, 16, 10)) мы переведём 156 из 10 в 16 систему счисления, а введя print(convert_base('23', 21, 4)) переведёт 23 из 4-ичной в 21-ичную систему (ответ: B).

Задача 2

Все задания беру из первого октябрьского варианта (он же вариант № 9325894) с сайта Решу.ЕГЭ.

Решение данной задачи совсем простое: банальный перебор.

print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы
for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1'
	for x in range(2):
		for z in range(2):
			for w in range(2):
				F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию
				print(x, y, z, F) #Выводим результат

Результат:

Нам вывелась вся таблица истинности (1 = True, 0 = False). Но это не очень удобно. Обратите внимание, что в задании, функция равно 0, так и давайте подправим код:

print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы
for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1'
	for x in range(2):
		for z in range(2):
			for w in range(2):
				F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию
				if not F:
					print(x, y, z, F) #Выводим результат

Результат:

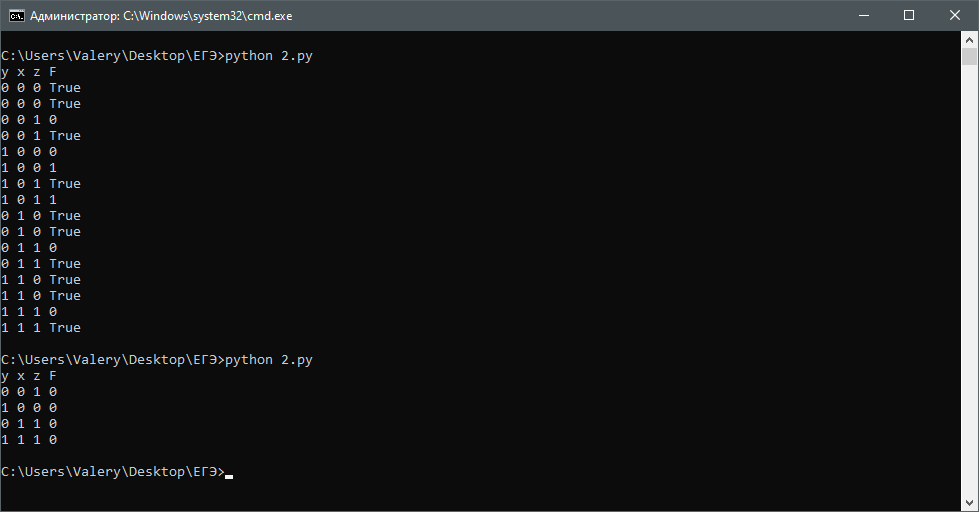
Далее - простой анализ.

Задача 5

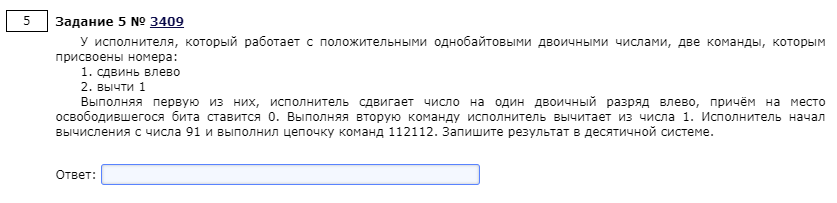
Данная задача легко решается простой последовательностью действий в интерпретационном режиме:

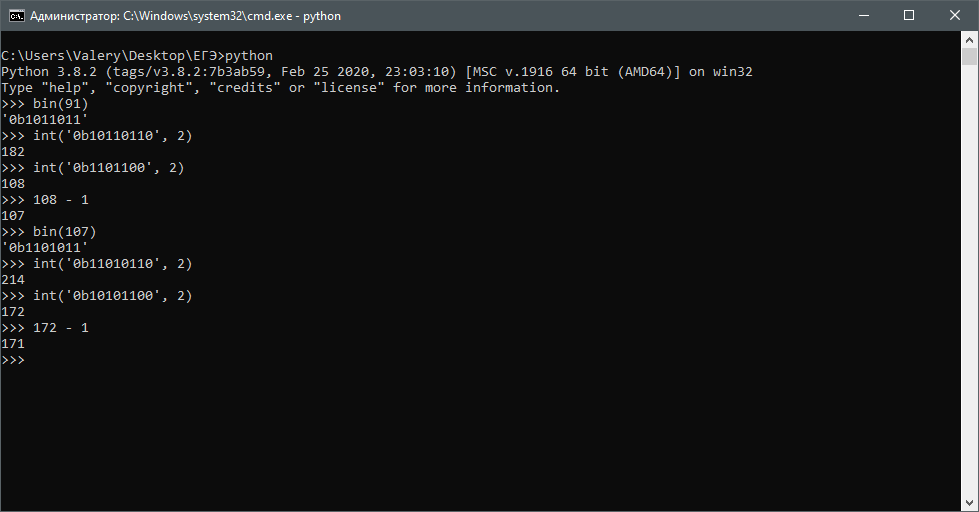
Задача 6

Перепечатали и получили ответ:

s = 0
k = 1
while s < 66:
    k += 3
    s += k
print(k)

Задача 12

В очередной раз, просто заменим слова на код:

a = '9' * 1000

while '999' in a or '888' in a:
	if '888' in a:
		a = a.replace('888', '9', 1)
	else:
		a = a.replace('999', '8', 1)
print(a)

Задача 14

Компьютер железный, он всё посчитает:

a = 4 ** 2020 + 2 ** 2017 - 15
k = 0

while a > 0:
    if a % 2 == 1:
    	k += 1
    a = a // 2

print(k)

Задача 16

Опять же, просто дублируем программу в python:

def F(n):
    if n > 0:
        F(n // 4)
        print(n)
        F (n - 1)
print(F(5))

Результат:

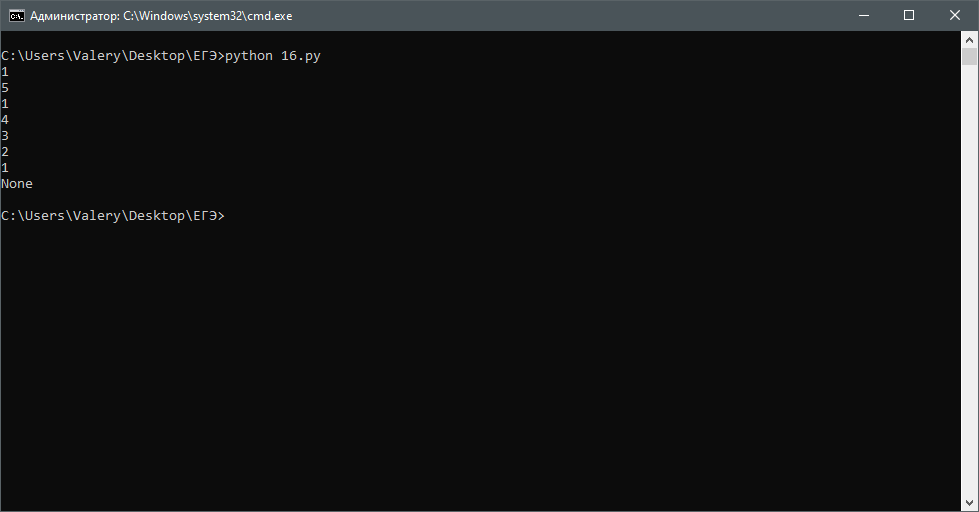
Задача 17

Задача с файлом. Самое сложное - достать данные из файла. Но где наша не пропадала?!

with open("17.txt", "r") as f: #Открыли файл 17.txt для чтения
    text = f.read() #В переменную text запихнули строку целиком
a = text.split("\n") #Разбили строку энтерами (\n - знак перехода на новую строку)

k = 0 #Стандартно обнуляем количество
m = -20001 #Так как у нас сумма 2-ух чисел и минимальное равно -10000, то минимум по условию равен -20000, поэтому...

for i in range(len(a)): #Обходим все элементы массива
	if (int(a[i - 1]) % 3 == 0) or (int(a[i]) % 3 == 0): #Условное условие
		k += 1 #Счётчик
		if int(a[i - 1]) + int(a[i]) > m: #Нахождение минимума
			m = int(a[i - 1]) + int(a[i])

print(k, m) #Вывод

Немного пояснений. Функция with() открывает файл считывает данные при помощи функции read() и закрывает файл. В остальном - задача стандартна.

Задача 19, 20 и 21

Все три задачи - задачи на рекурсию. Задачи идентичны, а вопросы разные. Итак, первая задача:

Пишем рекурсивную функцию и цикл перебора S:

def f(x, y, p): #Рекурсивная функция
	if x + y >= 69 or p > 3: #Условия завершения игры
		return p == 3
	return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or\
		   f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий

for s in range (1, 58 + 1): #Перебор S
	if f(10, s, 1): #Начали с 10 камней
		print(s)
		break

Немного пояснений. В рекурсивной функции существует 3 переменные x - число камней в первой куче, y - число камней во второй куче, p - позиция. Позиция рассчитывается по таблице:

Далее - всё по условию задачи.

Вторая задача на теорию игр:

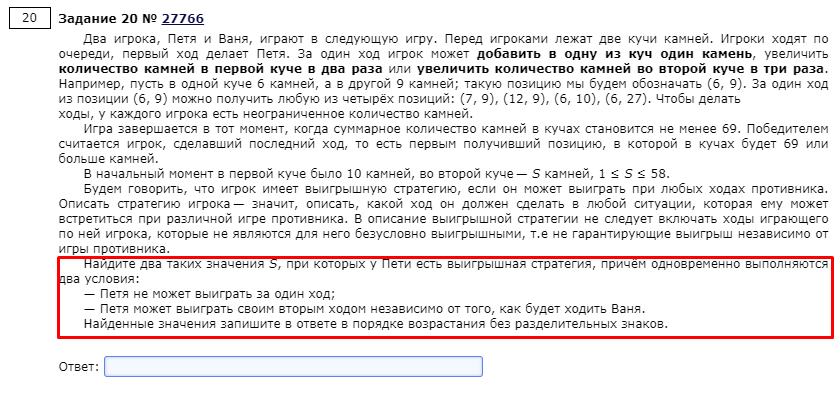
Все отличия в рамке. Ну и код, соответственно, не сильно отличается:

def f(x, y, p): #Рекурсивная функция
	if x + y >= 69 or p > 4: #Условия завершения игры
		return p == 4
	if p % 2 != 0:
		return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or\
			   f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
	else:
		return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and\
			   f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий


for s in range (1, 58 + 1): #Перебор S
	if f(10, s, 1): #Начали с 10 камней
		print(s)

Отличия:

1. Выиграл Петя, соответственно, позиция 4

2. Так как Петя не может выиграть за один ход - он выигрывает за 2 хода (and, а не or на нечётных позициях (играх Пети))

3. Убрали break, так как нам нужны все S, а не единственный

Последняя вариация задачи:

Сразу код:

def f(x, y, p): #Рекурсивная функция
	if x + y >= 69 or p > 5: #Условия завершения игры
		return p == 3 or p == 5
	if p % 2 == 0:
		return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or\
			   f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
	else:
		return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and\
			   f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий


for s in range (1, 58 + 1): #Перебор S
	if f(10, s, 1): #Начали с 10 камней
		print(s)

Ну и всего лишь 2 отличия:

1. Позиции 3 или 5, а не 4, так как выиграл Ваня

2. На второй ход выигрывает Ваня и нам нужно or и and поменять. Я заменил только кратность 2.

Задача 22

Ctrl+C, Ctrl+V - наше всё! :)

for i in range(1, 100000):
	x = i
	L = 0
	M = 0
	while x > 0 :
		L = L+1
		if (x % 2) != 0:
			M = M + x % 8
		x = x // 8
	if L == 3 and M == 6:
		print(i)

Задача 23

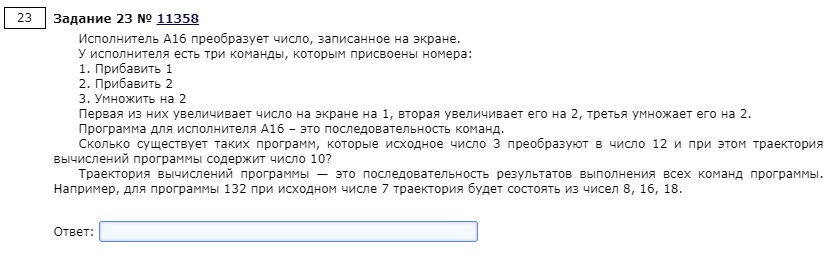
Итак, код:

def f(x, y):
	if x > y: #Перегнали цель
		return 0
	if x == y:  #Догнали цель
		return 1
	if x < y: #Догоняем цель тремя методами
		return f(x + 1, y) + f(x + 2, y) + f(x * 2, y)

print(f(3, 10) * f(10, 12)) #Прошло через 10, значит догнали 10 и от де догоняем 12

Так как в условии задачи мы увеличиваем число, но будем числа "догонять". Три метода описаны, ну а пройти через 10 - значит дойти до него и идти от него.

Собственно, это и есть вся первая часть ЕГЭ по информатике решённая на Python.

Ссылка на репозиторий со всеми программами:

Надеюсь, что смог помочь в своей статье выпускникам и готовящимся ;)

Остался один вопрос - нужен ли разбор второй части ЕГЭ по информатике на Python? Оставлю этот вопрос на ваше голосование.

Всем удачи!