02.01.2022 18:18
MagisterLudi 47 67000 Источник
image

Предлагаю поразмять мозги и как в прошлом году, порешать задачки с математической олимпиады в комментариях к этой статье. Задачек 6 штук, и на них отводилось 2 дня по 4,5 часа. (Чур, в ответы не подглядывать!)

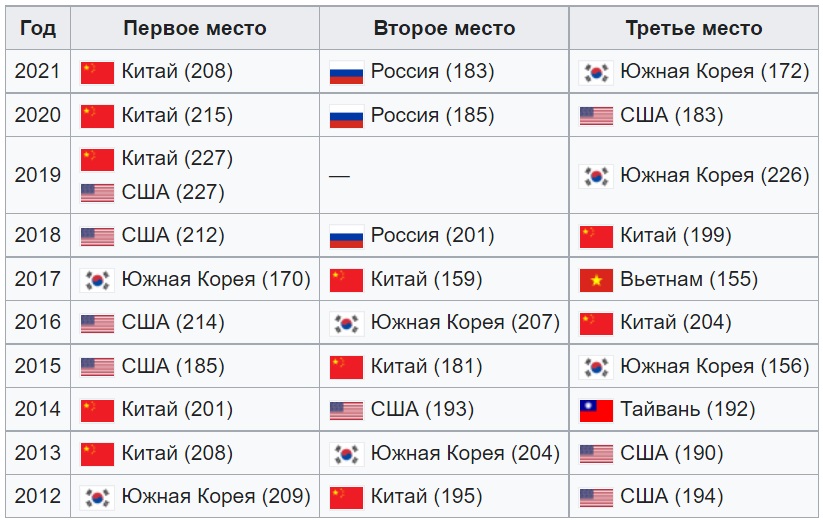
Этим летом в Питере прошла 62-я Международная математическая олимпиада с вот какими итогами:

  • Первое место заняла команда Китая, завоевавшая шесть золотых медалей (208 баллов).
  • Российские школьники заняли второе место с пятью золотыми и одной серебряной медалью (183 балла)
  • На третьем месте южнокорейская команда с пятью золотыми и одной серебряной медалью (172 балла)

Первая такая олимпиада прошла в 1959 году в Румынии, и тогда в ней принимали участие представители всего семи стран. В 2021 году в олимпиаде участвовали более 619 школьников из 107 стран.

image

Российская сборная
Тренировали сборную России учитель математики Президентского физико-математического лицея № 239 Санкт-Петербурга Кирилл Сухов, педагоги Центра педагогического мастерства Москвы Владимир Брагин и Андрей Кушнир. Россию на олимпиаде представляли:

  • Иван Бахарев (10 класс, Санкт-Петербург) — золотая медаль;
  • Айдар Ибрагимов (11 класс, Казань / Москва) — золотая медаль;
  • Матвей Исупов (11 класс, Ижевск) — золотая медаль;
  • Андрей Шевцов (11 класс, Москва) — серебряная медаль;
  • Данил Сибгатуллин (11 класс, Казань / Москва) — золотая медаль;
  • Максим Туревский (10 класс, Санкт-Петербург) — золотая медаль, абсолютное второе место в общем рейтинге.



День 1


Время на работу: 4 часа 30 минут.
Каждая задача оценивается в 7 баллов

Задача 1


Дано целое число n > 100. Ваня написал числа n, n+ 1,..., 2n на n+ 1 карточке, каждое по одному разу. Затем он перемешал колоду из этих карточек и разделил её на две стопки. Докажите, что хотя бы одна из двух стопок содержит две карточки, сумма чисел на которых — точный квадрат.

Задача 2


Докажите, что для любых вещественных чисел x1,..., xn выполняется неравенство

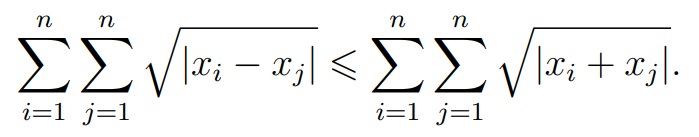
image


Задача 3


Точка D внутри остроугольного треугольника ABC, в котором AB > AC, такова, что
∠DAB = ∠CAD. Точка E на отрезке AC такова, что ∠ADE = ∠BCD; точка F на отрезке AB
такова, что ∠F DA = ∠DBC; точка X на прямой AC такова, что CX = BX. Точки O1 и O2 — центры
описанных окружностей треугольников ADC и EXD соответственно. Докажите, что прямые BC,
EF и O1O2 пересекаются в одной точке.

День 2


Время на работу: 4 часа 30 минут.
Каждая задача оценивается в 7 баллов

Задача 4


Дана окружность Γ с центром I. Выпуклый четырёхугольник ABCD таков, что каждый из отрезков AB, BC, CD и DA касается Γ. Пусть Ω — описанная окружность треугольника AIC. Продолжение отрезка BA за точку A пересекает Ω в точке X, продолжение отрезка BC за точку C пересекает Ω в точке Z. Продолжения отрезков AD и CD за точку D пересекают Ω в точках Y и T соответственно.

Докажите, что AD + DT + T X + XA = CD + DY + Y Z + ZC.

Задача 5


Чип и Дейл собрали на зиму 2021 орешек. Чип пронумеровал орешки числами от 1 до 2021 и вырыл 2021 маленькую ямку вокруг их любимого дерева. На следующее утро он обнаружил, что Дейл положил в каждую ямку по орешку, ничуть не беспокоясь о порядке. Расстроившись, Чип решил переупорядочить орешки посредством следующей последовательности из 2021 действия: во время k-го действия он меняет местами орешки, соседние с орешком под номером k.

Докажите, что найдётся такое число k, что во время k-го действия поменялись местами орешки с номерами a и b такими, что a < k < b.

Задача 6


Дано целое число m > 2. В конечном множестве A, состоящем из (не обязательно положительных) целых чисел, нашлись такие подмножества B1, B2, B3,..., Bm, что при каждом k = 1, 2,..., m сумма элементов множества Bk равна mk. Докажите, что A содержит хотя бы m/2 элементов.

Фотки команд
Олимпиада проходила дистанционно.


















Комментарии (47)


  1. RokeAlvo
    02.01.2022 18:42
    #23896275

    Задача 1.3

    Точно нет опечатки? Точки E и X лежат на прямой AC, а далее речь о треугольнике EXD


    1. tarekd
      03.01.2022 00:18
      #23897407
      +2

      нигде не сказано что точка D лежит на прямой AC


  1. shavluk
    02.01.2022 20:31
    #23896681
    +2

    Первая задача сводится наличию не менее трех пар карт "квадратов"


    1. telpos
      02.01.2022 23:23
      #23897283

      del


    1. 0xd34df00d
      03.01.2022 00:03
      #23897369

      Увы, не для любых n есть квадраты в интервале [n… n + 100]. Если конкретнее, как нетрудно видеть, начиная с n = 2602, есть довольно много таких интервалов.


      1. telpos
        03.01.2022 01:03
        #23897505
        +1

        в интервале [n… n + 100]

        в интервале [n, 2n]


        1. 0xd34df00d
          03.01.2022 01:19
          #23897539

          Перечитал условие… А, на каждой карточке может быть больше одного числа, что ли?


          1. telpos
            03.01.2022 01:31
            #23897553
            +6

            len([n, 2n]) == n+1


            1. 0xd34df00d
              03.01.2022 01:51
              #23897587
              +2

              Тьфу ты, я сегодня совсем идиот, спасибо.


    1. MiXei4
      03.01.2022 03:22
      #23897713

      Но ведь каждая из трёх пар может быть разбита и попасть в разные стопки?


      1. telpos
        03.01.2022 04:31
        #23897785

        Задача к сводится к наличию трёх чисел, попарно дающих квадраты


        1. Alexandroppolus
          03.01.2022 08:01
          #23897869
          +1

          Необязательно трех. Если считать числа вершинами графа, а квадратность суммы двух чисел ребром, то надобно убедиться, что в графе есть цикл нечетной длины (а значит граф не двудольный).

          Например, для 101 есть такой цикл длиной 5:

          159 -- 130 -- 126 -- 198 -- 202 -- 159


          1. telpos
            03.01.2022 11:34
            #23898217

            Это, конечно, так. Но у меня сложилось впечатление, что если есть такой цикл, то есть и упомянутая мной тройка чисел. Для n=101 это (126, 163, 198).


          1. dblokhin
            04.01.2022 09:56
            #23901367

            Круто.


          1. telpos
            04.01.2022 11:59
            #23901771
            +1

            Вот эти числа

            Красный: 126-163-198-126

            Зелёный: 159-130-126-198-202-159

            Тут всё наглядно видно


    1. gorilych
      04.01.2022 09:10
      #23901265

      если бы. Любое количество пар можно разбить на две разные стопки. Нужны не пары а связанные числа (тройки?), которые при любом раскладе дадут пару-квадрат в одной из стопок.


  1. Dmitry17
    02.01.2022 23:34
    #23897307

    Поспешишь, людей на смешишь


    1. AcckiyGerman
      02.01.2022 23:38
      #23897315

      Задача 1

      Дано целое число n > 100....


  1. nickerlan
    03.01.2022 02:14
    #23897621
    +1

    Вторая похожа на простую.


  1. Razoomnick
    03.01.2022 05:32
    #23897805
    +4

    Мои соображения по первой: она сводится к системе уравнений

    a+b=x^2

    a+c=(x+1)^2

    b+c=(x+2)^2

    с условиями целых корней a, b, c в интервале [n, 2n]

    эта система имеет корни (x^2-2x-3)/2, (x^2+2x+3)/2 и (x^2+6x+5)/2. Целые корни будут при нечетных x. Нас по сути интересует первое и последнее, (x^2-2x-3)/2 >= n, (x^2+6x+5)/2 <= 2n. Преобразуя эти неравенства, получим x^2-10x-11 >= 0, и соответственно x >= 11. Соответственно условие из исходной задачи выполняется при n >= 48


    1. Tyusha
      03.01.2022 10:00
      #23898009
      +1

      Браво!


    1. telpos
      03.01.2022 11:36
      #23898223
      +1

      Я проверил разные n на компьютере. Тройка (a, b, c) существует при n>98


      1. Razoomnick
        03.01.2022 18:54
        #23899587
        +1

        Вы правы. Похоже, n >= 48 это необходимое условие, над достаточным надо ещё подумать, пока ничего в голову не приходит.


      1. Razoomnick
        03.01.2022 23:30
        #23900353
        +3

        Получется не очень красиво, но мое полное решение пока выглядит так:

        Первая задача сводится к системе уравнений

        a+b=x^2

        a+c=(x+1)^2

        b+c=(x+2)^2

        с условиями целых корней a, b, c в интервале [n, 2n]

        эта система имеет корни a = (x^2-2*x-3)/2, b = (x^2+2*x+3)/2 и c = (x^2+6*x+5)/2. Целые корни будут при нечетных x. Теперь нас интересует, при каких n в интервале [n, 2*n] всегда найдется тройка целых чисел такого вида. По сути, поскольку a < b < c, то нас интересуют числа a и c. Это автоматически выполняется, когда a(x)*2 >= c(x+2) (это не умножение, а аргумент). То есть, когда (x+2)^2+6*(x+2)+5 <= 2*(x^2-2*x-3). Это неравенство имеет решение x >= 7+2*sqrt(19). Ближайшее нечетное целое - 17. Соответственно, утверждение доказано для с >= 198 и соответственно a >= 99 (n = a >= 99).


    1. unC0Rr
      03.01.2022 12:54
      #23898499
      +1

      Я решил так, найдя формулу для искомой тройки чисел:
      a = 2*t²–2
      b = 2*(t+1)²+1
      c = 2*(t+2)²–2
      где t — произвольное натуральное.
      Осталось показать, что для любого n > 100 найдётся такой t, что a, b и c укладываются в промежуток от n до 2*n. Для этого необходимо выполнение условия 2 * a(t) >= c(t + 1) при t > 8, т.е. что получаемые тройки находятся в пересекающихся интервалах. Подставляя формулы, получаем (t–3)² > 29, ч.т.д.


  1. Refridgerator
    03.01.2022 06:15
    #23897825
    +1

    По мне так задачки довольно скучные и как обычно, предельно оторванные от реальности. Выделять на их решение 9 часов жизни без какой-либо отдачи — так себе мотивация.

    Вот, например, как мне бы хотелось видеть подобные задачи — имеется равенство (строгого доказательства которого у меня нет):

    Функция интересна тем, что:

    1) в точках ±1 она равна ±1 и имет n-1 нулевых производных,
    2) обратной функцией для неё является он же при замене n на 1/n,
    3) монотонно возрастает в интервале от -1 до 1 при любых положительных n (а при отрицательных просто меняет знак),
    4) в варианте слева в точках ±1 возникает неопределённость в виде деления на ноль — но как его считать через предел непонятно — Mathematica в частности не знает,
    5) имеет отношение к преобразованию Мёбиуса и билинейному преобразованию в частности,
    6) появилась из сугубо практических задач.

    В таком случае, даже если не получилось её решить — то всё равно что-то новое узнаёшь и время потеряно не зря.


    1. N-Cube
      03.01.2022 08:02
      #23897871

      Воспользуйтесь неархимедовым анализом - когда бесконечно большие и малые не предел последовательности, а конечные числа, как физики всегда считали и считают (не так давно и математики перешли к формализму с пределом последовательности, что бессмысленно с точки зрения физики - поскольку есть мельчайшие неделимые частицы вещества, пространства и так далее). Тогда слева x=1 не будет проблемой. Кстати, справа зря переставили порядок слагаемых в числителе и знаменателе.


      1. Refridgerator
        03.01.2022 08:33
        #23897901

        справа зря переставили порядок слагаемых в числителе и знаменателе
        Это не я, это автоматический экспорт в Latex у Mathematica таким грешит. Сразу как-то не заметил, а потом уже поздно редактировать.


    1. 0o00oo00o0
      03.01.2022 13:58
      #23898703
      +3

      Функция в правой части определена везде, слева не определена только в единице, поэтому

      n > 0, x\ne 1,\; \begin{equation}1 - \frac{2}{(\frac{2}{1-x} - 1)^n + 1} = 1 - \frac{2}{(\frac{1 + x}{1 - x})^n + 1} =1 - \frac{2(1-x)^n}{(1+x)^n + (1-x)^n}=\end{equation}=\frac{(1 + x)^n - (1- x)^n}{(1 + x)^n + (1- x)^n}

      Слева предел в единице равен единице. Пусть x приближается к единице слева, тогда выражение в скобках стремится к "+бесконечности" (приближается справа - к "-бесконечности"). Независимо от четности n дробь стремится к нулю. От четности зависит направление стремления дроби к нулю.


      1. Refridgerator
        03.01.2022 15:00
        #23898873

        Хорошо, это было легко. Следующий уровень сложности — доказать, что n-1 производных в точках ±1 действительно равны нулю. Следующий уровень сложности — изменить функцию таким образом, чтобы требование равенства единице с заданным количеством нулевых производных выполнялось в произвольно выбранных точках. Следующий уровень сложности — дополнить новую функцию мнимой составляющей таким образом, чтобы её абсолютное значение при любом значении (действительного) аргумента было равно единице (без использования квадратного корня).


        1. N-Cube
          03.01.2022 15:38
          #23899017

          В гипердействительных числах не проблема. Наверное, не зря и Ньютон, в том числе, пользовался двусторонней производной и неархимедовым анализом:)


          1. Refridgerator
            04.01.2022 07:11
            #23901099

            «Не проблема» — значит, решение слишком очевидно, чтобы его озвучивать?


    1. Xaliuss
      04.01.2022 14:32
      #23902353
      +1

      Всё спокойно доказывается, достаточно одного семестра матана. Спокойно показывается например, что знаменатель стремится к бесконечности при x=1,значит вся дробь к 0, и выражение к 1. При x=-1 аналогично для отрицательных n.

      Вообще рекомендую прочитать какой-то нормальный курс анализа, если имеешь дело с такими вещами. В курсах для нематематиков очень часто пропущены важные детали, необходимые для понимания, почему делают так или иначе.


  1. NNTat
    03.01.2022 17:32
    #23899283

    Вторая задача странная. Выберем n=2, x_1=1, x_2=-1. Тогда левая часть будет больше правой.


    1. telpos
      03.01.2022 18:12
      #23899423
      +1

      i=j не учли


    1. unC0Rr
      03.01.2022 18:13
      #23899425

      Нет, не будет. Обратите внимание на итерацию по i и j.


    1. Razoomnick
      03.01.2022 18:58
      #23899599

      У меня получилось 4 = 4 для этого случая, т.е. нестрогое неравенство выполняется.


      1. telpos
        03.01.2022 23:04
        #23900275

        2\sqrt{2}\leq2\sqrt{2}


  1. Serg2769
    03.01.2022 21:16
    #23900003

    Однобокие все задачи. В основном числовые. Нет стереомерии


    1. Deepwarrior
      04.01.2022 18:29
      #23903189

      Стереометрия обычно сводится к выбору плоскости и планиметрии на ней, потому да, в олимпиады ее пихать скучно.


  1. Skala1970
    04.01.2022 01:11
    #23900643
    +2

    Мой коментарий не относиться напрямую к теме статьи. Но, про математику.... Лет эдак 25 тому назад я поступал в военную академию, и так как факультет был инженерный, то среди вступительных экзаменов была и высшая математика. И вот приехали мы на "абитуру" и стали готовиться к вступительным испытаниям. Сидим и всем потоком усердно изучаем теорию, и тут смотрю, а один товарищ из моей же войсковой части усердно решает какие-то прримеры. Как оказалось у него были варианты за прошедший год и не долго думая он поделился ими, включая ответы. Я тогда был еще молодой, мозги былы "не затуманены" лишней информацией и весь материал был успешно "выучен", что и помогло мне в дальнейшем получить высшее военное образование. По прошедствию 10 лет, после успешной защиты кандидатской диссертации я и сам стал преподавателем на своей "профильной" кафедре. И оказалось, что вопросы и ответы не меняються с "советских" времен, и большая часть кандидатов на поступление их "успешно" решают. Через некоторое время меня совместно с рядом преподавателей отправили в качестве экзаменаторов на "сборы" в один из округов. И как во все предыдущие годы мы просто "сверяли" ответы с "эталонами" и выставляли "зачет" или нет. Но один из моих старших товарищей, котрый нашу "доблестную" академию не заканчивал, от нечего делать, в один из скучных вечеров решил пересчитать задачи по "вышке", и был "очень удивлен" от осознания факта, что оказывается "эталонные" решения не только не правилльны, а в исходных данных отсутсвуют ряд необходимых переменных. Вот так, "тушите свет". Я не сомневаюсь, что на международной олимпиаде не может повториться даный "конфуз", но для меня это стало уроком, что любой "эталон" может содержать в себе кучу ошибок.


  1. LyutiyUtko
    04.01.2022 06:09
    #23901061
    -1

    Вторая прям простая. Бесконячность минус один < бесконечность плюс один. Ноль < бесконечность. Ноль< 2. Корни отбрасываем.


  1. Alex_Novosib
    04.01.2022 10:27
    #23901445
    +1

    Первый день, задача 2. Переписываем неравенство в виде

    A'+B'+С' <= A+B+C,

    где A и A' -- суммы, в который числа (xi и xj) имеют одинаковые знаки (но не равны друг другу), B и B' -- суммы, где числа имеют противоположные знаки (но не равны друг другу), C и C' -- суммы, где числа равны.

    Очевидно, что C'=0, C>=0, A'=B, B'=A.

    Что и требовалось доказать.


    1. Alexandroppolus
      04.01.2022 13:59
      #23902159

      [2, 4, -1, -3]

      A = 2 * ( sqrt(2 + 4) + sqrt(1 + 3) ) = 8.899

      B' = 2 * ( sqrt(2 + 1) + sqrt(2 + 3) + sqrt(4 + 1) + sqrt(4 + 3) ) = 17.6998

      A != B'


      1. unC0Rr
        04.01.2022 18:20
        #23903167

        В A так же входят такие выражения как 2-(-1), 4-(-3) и т.п., а в B' — 2-4, -1-(-3) и т.п.


        1. Alexandroppolus
          04.01.2022 19:29
          #23903359

          Нет, не входят. В А - только числа с одинаковыми знаками. И т.д.


  1. bestann
    04.01.2022 19:22
    #23903319

    Вот кому надо в ИТ идти.