Ссылка на статью в моем блоге

Данные в виде графа. Как их хранить? Как с ними работать?

Периодически возникают задачи и проекты, где данные имеют структуру графа. Например, данные о компьютерных сетях, где узлы связаны между собой. А на узлах зарегистрированы пользователи и они связаны или не связаны между собой. Еще пример — результат работы какого-то web crawler, который собирает данные из сети и хранит ссылки страниц между собой. Социальные сети. Список друзей, у которых тоже есть друзья — граф. Населенные пункты и дороги между ними — еще один пример графа.

Чтобы нам было удобнее давайте определимся с решаемой задачей. Допустим мы делаем систему администрирования некоторого сетевого ПО. Это ПО установлено на всех узлах сети. И из центра администрирования оно получает конфигурацию своей работы. Сети на практике большие, несколько администраторов одновременно могут включать и отключать связи между узлами. Либо напрямую, либо неявно через какие-то косвенные настройки. Наша задача обнаружить несвязанные сегменты в получившейся сети и не сохранить такую конфигурацию. Потому что плохая конфигурация приведет к неработоспособности.

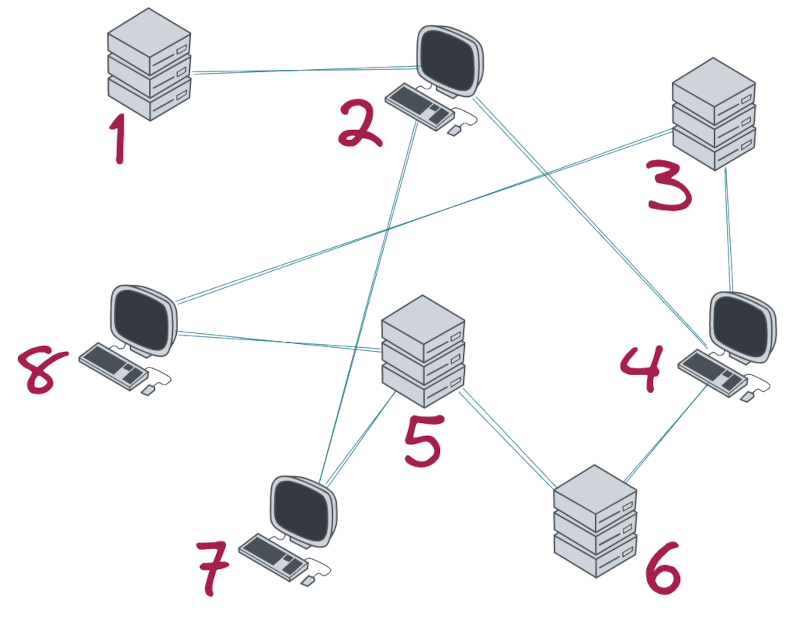
На схеме выше видно, что из любого узла сети есть как минимум один путь. Это хорошо.

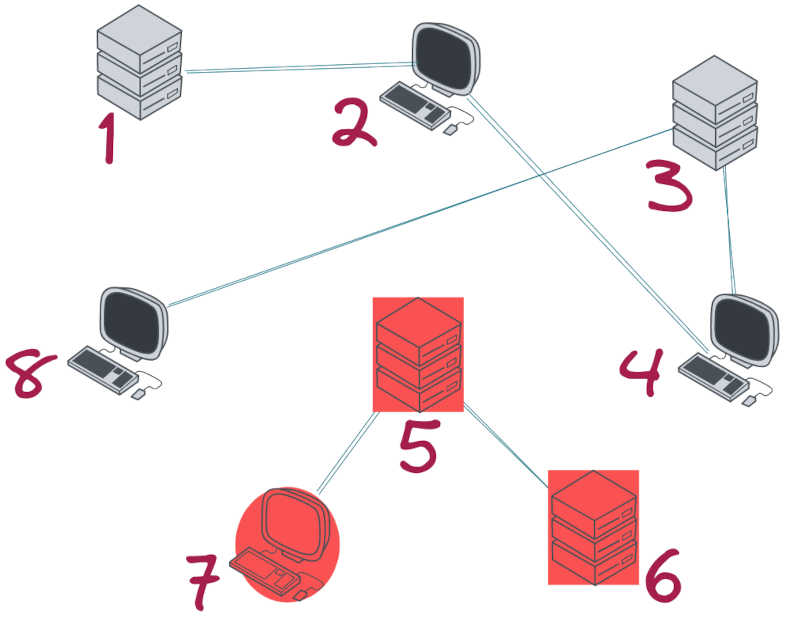
А вот на этой схеме дело плохо. Подсеть из узлов 7,5,6 — не доступна для другой части сети. И такую конфигурацию отправлять нельзя.

Когда мы познакомились с задачей давайте попробуем порассуждать о способе хранения информации о сети. Очевидный формат — это использование реляционного хранилища. В нем можно завести таблицу с описанием узлов сети (Идентификатор, Название узла, Время включения в сеть, Название операционной системы и т.п.). Но нам более интересно как хранить связи этих узлов. Можно создать таблицу со списком связей node_to_node (пример для рисунка выше):

Здесь все просто — идентификатор первого узла, идентификатор второго узла и какие-то свойства связи (скорость задержки от узла к узлу). Естественно оба столбца нужно проиндексировать. Идентификатор выберем типа int. Нужно определиться представляем ли мы связь одной записью или двумя. В случае если мы храним одну запись код проверки будет несколько сложнее:

select 1 from node_to_node where node1_id = 1 and node2_id = 2
union all
select 1 from node_to_node where node1_id = 2 and node2_id = 1

Если же хранится и перевернутая запись — объем данных в два раза больше, но код проверки уменьшается:

select 1 from node_to_node where node1_id = 1 and node2_id = 2

Еще можно внести условие, что записи хранятся в виде node1_id < node2_id. Но это только если у вас численные идентификаторы. Но стоит ли об этом задумываться? Выглядит как мелочь. И так и так можно…

Сюрприз

PostgreSQL эффективен в большинстве сценариев. Применительно к нашей задаче все сильно зависит от объема сети. Если у нас есть сеть из 65536 узлов и каждый из них связан с каждым мы получаем 4294967296 связей. Нам нужно 64Гб на то, чтобы сохранить все связи. Либо даже 128Гб для случая если мы храним еще и перевернутую запись (см. выше). Причем таблица связей будет в центре бизнес-логики. Время выполнения проверки имеет большое значение. Разница между 2 мс и 300 мс в конечном счете будет накапливаться и вы получите откровенно не работоспособные сценарии. Мало кто согласиться ждать 2 дня для проверки целостности сети.

Какие могут быть решения? Можно попробовать хранить связи как матрицу смежности. Где каждый бит обозначает наличие связи между узлами.

Тут вполне можно обойтись 512 Мб памяти и это будет быстрее. Но и тут проблемы. Код такого движка надо писать. При этом нужно учитывать возможность многопользовательского режима. Транзакционности и отказоустойчивости.

Вероятно сейчас уже появились такие решения. Несколько лет назад мне их найти не удалось. Напишите в комментариях что вы рекомендуете.

Существует целый класс графовых баз данных Graph Databases. Самая популярная из которых Neo4j. Но и тут решения проблем производительности нет. Зато есть очень выразительный язык запросов, который сильно упрощает их написание. Да и читабельность кода повышается.

Идея решения

Существует несколько алгоритмов сжатия графов. Применительно к нашей ситуации интерес представляет алгоритм выделения “виртуальных узлов”, которые заменяют собой “сгустки” связей.

Пусть у нас есть вот такая сеть:

Здесь мы видим, что есть два ряда узлов, где каждый из узлов ряда связан с узлами из другого ряда. Всего в такой сети 35 связей.

Если мы поставим между этими рядами некоторый привнесенный, вымышленный узел. То все узлы по прежнему будут связаны через него. Будем называть такие узлы виртуальными.

На рисунке ниже можно видеть результат. Общее число связей уменьшилось до 20. И плюс один узел “виртуальный узел”.

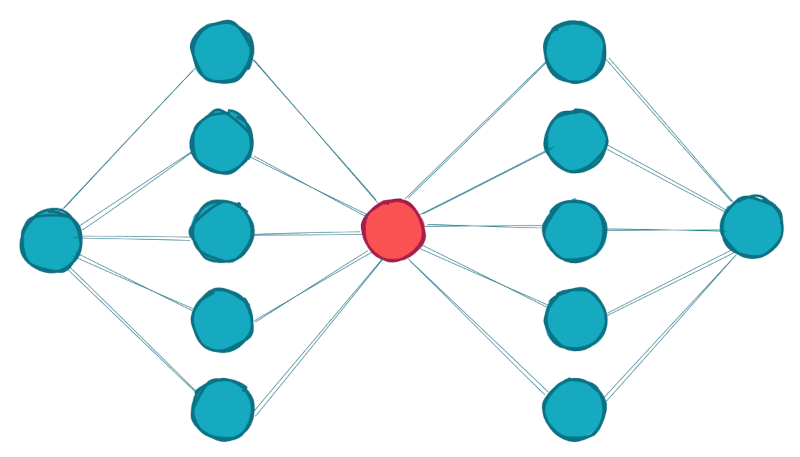
Понятно, что для сетей такой размерности нет никакого смысла экономить 15 связей из 35. Но чем больше в такой сети подобного рода “сгустков связей”, тем больше экономия. Для нашего экстремального случая из примера выше, где 65536 узлов связаны все со всеми, мы вместо 64Гб для хранения такой сети нужно всего лишь 1 Мб. Все операции будут “летать”. :)

Замеры производительности

Давайте посмотрим как будет меняться скорость для сжатых и не сжатых сетей. Для примера возьмем сеть из рисунка выше (с двумя рядами узлов). И будем искать кратчайший путь из начального узла в конечный. Для этого можно использовать следующий код:

WITH RECURSIVE search_graph(      
  node1,   
  node2,   
  depth,
  path) AS (      
    SELECT    
    g.node1,   
    g.node2,   
    1 as depth,
    ARRAY[g.node1] as path
    FROM node_to_node AS g       
    WHERE node1 = 30 -- старт
    UNION ALL      
    SELECT  
      g.node1,
      g.node2,
      sg.depth + 1 as depth,
      path || g.node1 as path
    FROM node_to_node AS g, search_graph AS sg
    WHERE g.node1 = sg.node2
        AND (g.node1 <> ALL(sg.path))
  )      

SELECT * FROM search_graphwhere node2 = 1003 -- финиш
limit 1;

В случае с виртуальным узлом нужно добавить еще и проверку на признак виртуальности. И в алгоритме поиска воспринимать его как технический узел, который не удлиняет путь между узлами.

Из таблицы видно насколько внушительно уменьшается число связей. По сжатому графу PostgreSQL работать в разы легче.

Но это все искусственный тест. Хотелось бы посмотреть что происходит с реальными данными. В сети полно открытых источников Laboratory for Web Algorithmics. Давайте возьмем наименьший датасет cnr-2000 (Italian Consiglio Nazionale delle Ricerche domain). В нем 3216152 связей. А в результате сжатия у меня вышло 1612981 связей и 100 виртуальных узлов. То есть ровно в два раза, точнее 1,9939 :). На скорости это сказалось аналогичным образом. Если на не сжатой сети мы получали время выполнения запроса 350 мс, то на сжатой он выполнялся уже за 150 мс.

Как реализовать такой алгоритм сжатия?

Мы убедились, что можно получить прирост скорости. Дело осталось за малым — реализовать такое сжатие. Сам алгоритм подробно описан в статье Gregory Buehrer, Kumar Chellapilla. A Scalable Pattern Mining Approach to Web Graph Compression with Communities. Она легко ищется в интернете.

Общая идея описывается в несколько предложений. Сначала мы разбиваем исходных граф на кластеры с похожим набором связей. Для каждого кластера строим суффиксное дерево со списком вершин-кандидатов для генерации виртуальных узлов. Считаем потенциальное сжатее для каждого из кандидатов и выбираем наилучший. И так продолжаем, пока кандидатов не останется. Не вижу надобности описывать сейчас этот алгоритм подробнее. Ссылку на статью привел выше. Но если будет потребность в этом — могу сделать в одной из следующих статей. Пишите в комментариях - нужно это или нет.

Выводы

Графы хоть и встречаются на проектах, но не очень часто. Чаще приходится иметь дело с обычной реляционной структурой данных. Но даже если у вас графовые данные. Вовсе не означает, что описанный выше способ вам подойдет. Нужно учитывать насколько статична структура данных, насколько в данных велика избыточность. Но вот если после всего этого анализа вы пришли к выводу, что это ваш случай. Можно получить ощутимый выигрыш в скорости и в объеме БД.