Привет, друзья!

Представляю вашему вниманию адаптированный и дополненный перевод этой замечательной статьи.

В данной статье я хочу рассказать вам о некоторых основных математических концепциях и их обозначениях, а также показать примеры реализации этих концепций на JavaScript.

Символы точки и креста

Символы точки и креста являются очень распространенными в математике, но их использование зависит от контекста.

Умножение скаляров

Оба символа могут представлять простое умножение скаляров. Следующие выражения эквиваленты:

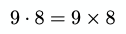
В JS для умножения используется астериск (*):

const result = 9 * 8;

Знак умножения в выражении часто опускается:

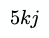
Если переменные k и j являются скалярами, код будет выглядеть так:

const result = 5 * k * j;

Умножение векторов

Для умножения векторов часто применяется символ открытой точки (∘). Этот символ представляет произведение Адамара:

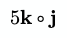
Это может быть реализовано следующим образом:

function multiply(a, b) {
  return [a[0] * b[0], a[1] * b[1]];
}

function multiplyScalar(a, scalar) {
  return [a[0] * scalar, a[1] * scalar];
}

const s = 5;
const k = [1, 2];
const j = [2, 3];

const v = multiply(k, j);
const result = multiplyScalar(v, s);
// [ 10, 30 ]

Скалярное произведение

Символ точки может обозначать скалярное произведение двух векторов:

Код будет выглядеть так:

function dot(a, b) {
  return a[0] * b[0] + a[1] * b[1] + a[2] * b[2];
}

const k = [0, 1, 0];
const j = [1, 0, 0];

const result = dot(k, j);
// 0

0 означает, что векторы являются перпендикулярными.

Векторное произведение

Символ креста может обозначать векторное произведение двух векторов:

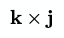
Код будет выглядеть так:

function cross(a, b) {
  const ax = a[0],
    ay = a[1],
    az = a[2],
    bx = b[0],
    by = b[1],
    bz = b[2];

  const rx = ay * bz - az * by;
  const ry = az * bx - ax * bz;
  const rz = ax * by - ay * bx;
  return [rx, ry, rz];
}

const k = [0, 1, 0];
const j = [1, 0, 0];

const result = cross(k, j);
// [ 0, 0, -1 ]

Сигма

Символ сигмы (Σ) используется для суммирования:

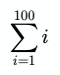
Здесь i=1 означает, что сложение начинается с 1 и заканчивается числом над сигмой, т.е. 100. Это верхняя и нижняя границы, соответственно. i справа от Σ говорит о том, что именно суммируется. Код будет выглядеть следующим образом:

let sum = 0;
for (let i = 1; i <= 100; i++) {
  sum += i;
}
// 5050

Чуть более сложный пример:

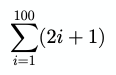
Код:

let sum = 0;
for (let i = 1; i <= 100; i++) {
  sum += 2 * i + 1;
}
// 10200

Сигмы могут быть вложенными. При этом, выражение оценивается справа налево (сначала вычисляется крайняя справа сигма, затем вторая справа и т.д.), если для изменения порядка оценивания не используются круглые скобки:

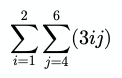
Код:

let sum = 0;
for (let i = 1; i <= 2; i++) {
  for (let j = 4; j <= 6; j++) {
    sum += 3 * i * j;
  }
}
// 135

Заглавная П

Заглавная П или "Большая П" похожа на сигму, только вместо суммирования для вычисления результата последовательности значений используется умножение:

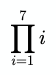
Код:

let product = 1;
for (let i = 1; i <= 7; i++) {
  product *= i;
}
// 5040

Брусья

Символ брусьев (| |) также может обозначать разные вещи в зависимости от контекста. Три основных случая использования: абсолютная величина, Евклидова норма и определитель. Все они описывают длину объекта.

Абсолютная величина

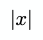
Это означает абсолютное величину или модуль числа x. В JS это будет выглядеть так:

const x = -4;
const result = Math.abs(x);
// 4

Евклидова норма

Евклидова норма или просто норма касается векторов. Это "величина" или "длина" вектора.

Пример использования массива [x, y, z] для представления трехмерного вектора:

function length(vector) {
  const x = vector[0];
  const y = vector[1];
  const z = vector[2];
  return Math.sqrt(x * x + y * y + z * z);
}

const result = length([0, 6, -8]);
// 10

Определитель

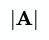
Пример вычисления определителя или детерминанта матрицы 2x2, представленной одномерным (плоским) массивом:

function determinant(a) {
  return a[0] * a[3] - a[2] * a[1];
}

const result = determinant([1, 0, 0, 1]);
// 1

Циркумфлекс

Символ циркумфлекса (^), который также называют "крышечкой" или "домиком" ("hat"), часто применяется в геометрии для обозначения единичного вектора. Пример единичного вектора a:

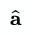
В прямоугольной системе координат или Декартовом пространстве единичный вектор, обычно, имеет длину, равную 1. Это означает, что каждая часть вектора будет находиться в диапазоне от -1.0 до 1.0. Пример преобразования ("нормализации") трехмерного вектора в единичный:

function normalize(vector) {
  const x = vector[0];
  const y = vector[1];
  const z = vector[2];
  const squaredLength = x * x + y * y + z * z;

  if (squaredLength > 0) {
    const length = Math.sqrt(squaredLength);
    return [x / length, y / length, z / length];
  }
  return vector;
}

const result = normalize([0, 8, -6]);
// [ 0, 0.8, -0.6 ]

Элемент

В теории множеств символы ∈ и ∋ часто используются для описания принадлежности элемента какому-либо множеству. Например:

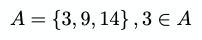
Имеем множество чисел A { 3, 9, 14 } и утверждаем, что 3 является элементом этого множества.

Простая реализация:

const A1 = [3, 9, 14];

const result1 = A1.includes(3);
// true

const A2 = new Set([3, 9, 14]);

const result2 = A2.has(14);
// true

Символ ∋ — это тоже самое, только меняется порядок (это называется зеркальным отображением):

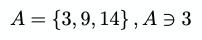
Для обозначения того, что значение не является элементом множества используются символы ∉ и ∌.

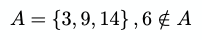
Для тех, кому интересно, вот полная таблица основных математических символов.

Функции

Функции являются ключевой частью математики. Они легко преобразуются в код.

Функция — это описание того, что следует сделать с входным значением для получения результата. Пример функции:

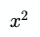
Названием данной функции может быть, например, ƒ или A(x):

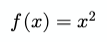
В коде функцию можно (и даже нужно) именовать более осмысленно:

const square = (x) => Math.pow(x, 2);

Функция может принимать несколько параметров. В математике параметры функции называются аргументами. Количество аргументов определяет "арность" (arity) функции (для уменьшения арности функции применяется техника под названием "каррирование" / currying; как правило, данная техника используется для создания частично-применяемых / partial функций):

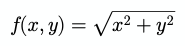
Код:

const length = (x, y) => Math.sqrt(square(x) + square(y));

Кусочно-заданная функция

Функции могут состоять из трех основных частей: аргументы, отношение и результат (такие функции называются кусочно-заданными). Отношение определяет зависимость между аргументами и результатом. В некоторых функциях отношение определяется аргументами. Следующая функция ƒ делает выбор между двумя "подфункциями" на основе аргумента:

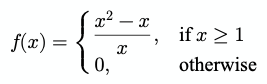
В коде для этого можно прибегнуть к помощи if / else:

function f(x) {
  if (x >= 1) {
    return (square(x) - x) / x;
  }
  return 0;
}

Основные функции

Наиболее распространенные математические функции представлены в JS встроенными функциями типа parseInt или parseFloat и методами объекта Math.

Пример функции знака или функции sgn в кусочно-заданной нотации:

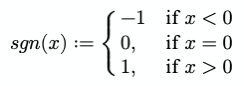
const sgn = (x) => Math.sign(x);
// полифил
function sgn(x) {
  x = +x
  if (x === 0 || isNaN(x)) {
    return x;
  }
  return x > 0 ? 1 : -1;
}

Функции округления

Специальные скобки ⌊ ⌋ и ⌈ ⌉ представляют функции округления в меньшую и большую сторону, соответственно:

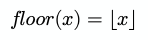
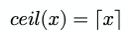
Код:

Math.floor(x);
Math.ceil(x);

Смешанные скобки ⌊ ⌉, как правило, представляют функцию округления до ближайшего целого числа:

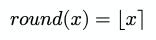
Код:

Math.round(x);

Послесловие

Мы рассмотрели лишь верхушку айсберга. Для тех, кто хочет погрузиться в тему применения математики в коде глубже, советую взглянуть на этот репозиторий.

Пожалуй, это все, чем я хотел поделиться в данной статье. Надеюсь, вы, как и я, нашли для себя что-то интересное и не зря потратили время.

Благодарю за внимание и happy coding!

---