В настоящее время в интернете можно найти сайты с визуализацией некоторых квантовых процессов. Я решил сделать свой сайт с визуализацией квантового спина. Расскажу, как появилось желание сделать этот сайт и что на нем находится.
Много лет тому назад в институте в курсе общий физики в третьем семестре нам что-то рассказывали про квантовую механику. Что именно рассказывали – я совершенно не помню. Однако, сама эта наука в силу своей загадочности меня чем-то заинтересовала. По возможности, я покупал самые простые научно-популярные книги (реже - более сложные с некоторым количеством формул) на эту тему и даже иногда прочитывал несколько страниц перед сном (возможно для того чтобы побыстрее заснуть).
Начиная примерно с 2018 года на глаза стали регулярно попадаться статьи в интернете про появление настоящих квантовых компьютеров. Во многих из этих статей говорилось, что квантовые компьютеры и квантовые вычисления в самое ближайшее время получат массовое распространение. Меня эти статьи заинтриговали и я решил познакомиться с этой темой более глубоко. У меня была когда-то и зачем-то, сам не знаю, куплена книга Ландау и Лифшица “Квантовая механика” которая, как я прочитал пользуется огромным уважением не только в нашей стране, но и во всем мире. Естественно, я решил ее почитать. После попытки прочтения первых страниц, стало понятно, что эта книга написана гениями и для гениев или, по крайней мере, для людей, которые уже довольно хорошо разбираются в данным предмете.
Короче для меня эта книга совершенно не подходила. На английском языке я нашел в интернете довольно много книг по квантовой механике и квантовым вычислениям написанных достаточно простым языком и весьма понятно. Естественно, желательно было найти подходящие книги или статьи на русском языке. И такие источники информации нашлись.
Прежде всего эта книга Леонарда Сасскинда и Арта Фридмана "Квантовая механика. Теоретический минимум". Это очень понятно написанная книга с применением простой (но не упрощенной) математики.
Видеолекции на youtube на канале LightCone просто превосходны. Автор замечательно рассказывает про квантовую механику, ее математику и теорию групп.
Книги Роджера Пенроуза. Этих книг несколько. Они перечислены в пятой главе моего сайта. Книги Пенроуза ни в коем случае не являются учебниками. Но они пытаются, именно, объяснить основные моменты в квантовой механики.
И, конечно, классическая книга Ричарда Фейнмана "Квантовая механика" из его курса лекций.
После прочтения первых глав книги "Квантовая механика. Теоретический минимум" у меня сразу возникла мысль, что неплохо бы сделать визуализацию эксперимента Штерна-Герлаха. Этот эксперимент является одним из основных в квантовой механике и упомянутая книга использует результаты этого эксперимента в качестве основы для создания последовательной квантовой теории. Я сразу решил, что визуализация не должна быть в виде exe-файла, а должна быть расположенной на сайте и быть интерактивной. Поэтому для создания программы была выбрана библиотека three.js и язык javascript. Кроме того, я решил добавить на сайт подробное рассмотрение некоторых, на мой взгляд, самых сложных моментов касающихся квантового спина.
После того как была закончена работа по созданию визуализации эксперимента Штерна-Герлаха, я сделал еще несколько прграмм и снабдил их соответствующим текстом. Ссылка на сайт, где находятся программы Визуализация квантового спина. Каждая программа помещена в отдельной главе. Всего таких глав шесть.
Первая глава данного сайта содержит программу виртуального эксперимента Штерна-Герлаха. Я старался сделать программу максимально совпадающую по своим возможностям с реальным физическим экспериментом. Интерактивно можно задавать параметры при проведении виртуального эксперимента и сразу получать его результаты. При создании программы я в основном руководствовался описанием эксперимента в книге Сасскинда и Фридмана.
Во второй главе представлена небольшая интерактивная программа поясняющая важный факт на который, почему-то, обычно не обращают особого внимания. Смысл этого факта заключается в следующем. В процессе проведения эксперимента Штерна-Герлаха мы получаем результаты, которые при желании можно представить противоположно направленными векторами. Но в математике квантовой механики противоположность векторов заменена на их ортогональность. Это приводит к далеко идущим последствиям. Появляется возможность ввести скалярное произведение векторов и использовать все возможности линейной алгебры. Появляются половинные, или наоборот двойные углы - смотря с какой стороны на это посмотреть. Но при этом появляется необходимость различать реальное физическое пространство, в котором находится электрон, и математическое (спинорное) пространство в котором математически описывается вращение этого электрона. Если в спинорном пространстве электрон делает один оборот, то в физическом пространстве этот же электрон делает на самом деле два оборота. Во второй главе также приводится перевод небольшой заметки Сасскинда, в которой затронута эта тема.
В третьей главе представлена интерактивная программа, которая демонстрирует половинные углы при описании поворотов электрона в спинорном пространстве. Как уже говорилось, появление половинных углов является прямым следствием замены противоположно направленных векторов на ортогональные векторы. В этой главе, и в интерактивной программе из нее, особое внимание уделено выбору базисных векторов, которые будут использоваться в следующей главе в 3D-программе визуализирующей повороты электрона в физическом и спинорном пространствах.
В четвертой главе приводится 3D-программа позволяющая наблюдать повороты электрона в физическом и спинорном пространствах. Одновременно можно увидеть соответствующие значения вектора состояния квантовой системы. В некотором смысле эта программа подобна программе визуализации сферы Блоха. Однако, на мой взгляд, она более ясно демонстрирует изменения вектора состояния при одновременной визуализации поворотов электрона как в физическом, так и в спинорном пространствах.
Также в этой главе приводятся подробные решения трех задач из книги Сасскинда и Фридмана (в книге нет их решений). Эти задачи наглядно демонстрируют некоторые важные моменты квантовых вычислений, которые понадобятся в шестой главе, которая посвящена квантовым вращениям. При рассмотрении решения этих задач очень хорошо проявляется смысл собственных векторов и собственных значений квантовых операторов.
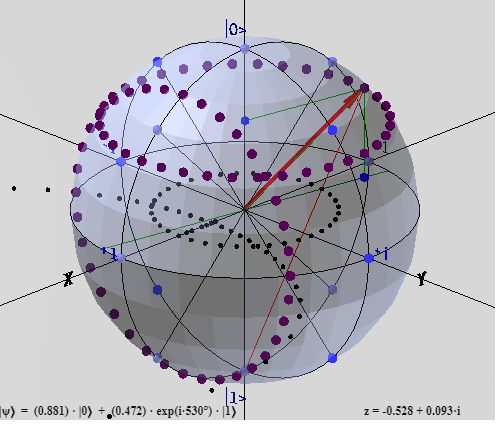
В пятой главе рассматривается сфера Блоха - Римана - Пуанкаре. Приводится соответствующая интерактивная программа. В этой главе я хотел коснуться теории спиноров, но решил, что лучше сделать перевод некоторых глав из книги, которая, в отличие от других книг и статей, как мне кажется, наиболее понятно объясняет эту теорию. Ссылка на перевод есть в тексте данной главы.
В шестой главе с помощью программы приведенной в ней можно увидеть визуализацию трехмерных вращениий на сфере Блоха - Римана - Пуанкаре. Одновременно в программе осуществляется дробно-линейное преобразование и, как следствие этого, вращения отображаются не только на сфере, но и на комплексной плоскости. Возможно, зта самая интересная программа из приведенных на данном сайте. Также в программе можно увидеть вращение вектора Блоха, которое осуществляется при помощи трех матриц Паули и матрицы Адамара. Приводятся математические вычисления используемые при описании этих вращений.
Программы из первой, четвертой, пятой и шестой глав выполнены при помощи библиотеки three.js позволяющей работать с технологией webgl. Программы из второй и третьей главы сделаны на основе HTML5 Canvas. При создании программ этого сайта я пользовался своими, ранее сделанными сайтами, которые можно увидеть по ссылкам Three.js и геометрия и Canvas и геометрия.
Достаточно неприятным моментом при создании трехмерных программ стала задача согласования системы координат принятой в three.js с системой координат принятой при описании поворотов спина в квантовой механике. Использование половинных углов в спинорном пространстве также требовало повышенной внимательности, чтобы случайно не перепутать эти углы с углами в физическом пространстве.
Программы данного сайта и другие мои программы можно увидеть на моем репозитарии.

