В данной статье рассмотрено применение геометрической библиотеки функций WebGeometry для построения моделей сложных многогранников. Библиотека написана на языке Javascript. Ссылка на GitHub с примером, в котором приведен простейший пример использования библиотеки. Замечания и критика приветствуются.
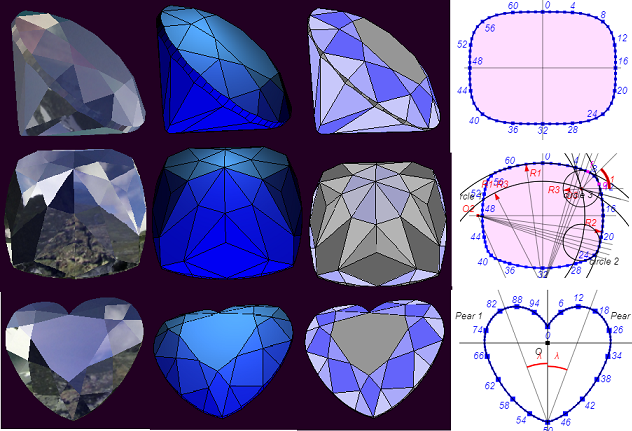
Для отображения моделей, предварительно рассчитанных с помощью функций из библиотеки WebGeometry, применяется библиотека ThreeJS. Холст (canvas) HTML5 используется для показа отдельных плоских элементов моделей и вывода на экран вспомогательной информации.
Технология WebGL и библиотеки созданные на ее основе, такие как ThreeJS и BadylonJS, используются в интернете для реализации самых разных целей, связанных с 3D графикой. Но в основном они находят применение для отображения в браузере уже готовых трехмерных моделей (предварительно созданных, например, в программах 3ds Max или Blender). Если перед нами встает задача создания параметрической модели, то есть такой модели, у которой, в процессе отображения в браузере уже готового объекта, мы можем изменить его отдельные элементы при помощи задания соответствующих параметров модели (например увеличить угол наклона некоторой грани), нам необходимо иметь набор геометрических функций, которые позволят создать модель таким образом, чтобы в дальнейшем существовала возможность интерактивно варьировать форму отдельных элементов модели или в целом всей модели. Для решения этой задачи нам потребуется набор функций на языке Javascript, которые будут реализовывать методы применяемые в аналитической геометрии. В библиотеке должны присутствовать функции для создания прямых, плоскостей и окружностей, нахождения точек (или прямых) пересечения их между собой, создания наклонных плоскостей и многое другое. В библиотеках ThreeJS и BadylonJS некоторые из этих возможностей присутствуют, но количество осуществляемых с помощью них действий не позволит выполнить все возникающие задачи при построении параметрической модели. Существуют еще несколько чисто математических Javascript библиотек. Из них наиболее широкое распространение получили glMatrix и Sylvester. Библиотека glMatrix в основном предназначена для работы с векторами, матрицами и кватернионами, но функций для работы с прямыми и плоскостями в ней нет. В библиотеке Sylvester эти функции есть, но присутствуют они в достаточно ограниченном количестве. Однако существует несколько книг в которых описана реализация методов аналитической геометрии на языке C/C++. Соответствующие программы на C/C++ можно использовать как прототипы при создании математической библиотеки на Javascript. Поэтому, когда я решил создать трехмерные параметрические модели огранок алмазов для отображения их в браузере, библиотека ThreeJS была выбрана мной только для вывода на экран уже рассчитанных моделей — для расчета формы моделей она не использовалась. Для самого расчета формы была создана библиотека WebGeometry. За основу этой библиотеки были взяты ранее использованные мной геометрические функции на C/C++, которые я перевел на язык Javascript. Рассмотрим этапы построения модели пирамиды (огранка алмаза типа Pyramid).
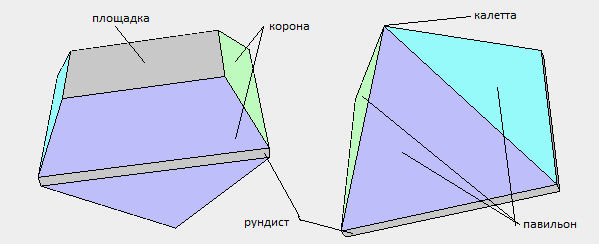
На первом этапе нам надо нарисовать предполагаемый вид модели и затем пронумеровать ее вершины. На приведенном рисунке приведена нумерация вершин и названия элементов огранки входящих в состав модели огранки пирамиды.

После этого требуется из пронумерованных вершин образовать грани. Например для грани площадки и граней короны следует записать следующую последовательность вершин (дублированная первая вершина грани сигнализирует о том, что грань закончилась):
Обход граней следует производить против часовой стрелки. В файле pyramid_index.js приведен исходный текст обхода всех граней пирамиды и подробные комментарии. Результат обхода записывается в массив index_cut.
На втором этапе мы можем раскрасить грани модели. Этот этап не является обязательным, если раскраска нам не нужна. Предположим, что мы хотим раскрасить модель пирамиды следующим образом:
С этой целью создается файл pyramid_colors.js в котором находится функция facet_colors() которая осуществляет запись цветов всех граней в массив colors.
На третьем этапе, после того как пронумерованы все вершины и записаны последовательности обхода всех вершин граней, необходимо задать параметры модели и затем произвести расчет координат всех ее вершин. Конечно, предполагается что мы уже наметили для себя алгоритм построения и придумали как будут расположены в пространстве все грани модели. Для пирамиды мы выберем следующие параметры, которые будут задавать размеры как отдельных ее частей, так и всей модели в целом:
Выбор параметров определяется разработчиком модели. Например, вместо задания двух параметров для двух углов наклона короны, можно задавать единственный параметр сразу для двух углов – тогда эти углы всегда будут одинаковыми. Можно ввести параметр определяющий размер площадки. В этом случае требуется либо не задавать высоту короны, либо не задавать наклон ее граней. Еще один вариант выбора параметров состоит в том, чтобы некоторые параметры сделать вычисляемыми. В этом случае при изменении одних параметров некоторые другие могут менять свое первоначальное значение. Например, если предположить, что для пирамиды мы определили один параметр для задания угла наклона граней короны, другой параметр для высоты короны и и еще один параметр, который будет задавать размер площадки, то при изменении наклона граней мы будем вынуждены изменять либо размер площадки, либо высоту короны. С другой стороны, если изменить параметр задающий размер площадки, то автоматически изменится значение параметра задающего либо высоту, либо наклон граней короны. Вариант связанный с применением вычисляемых параметров в данной программе, а также и при построении остальных моделей огранок, приведенных на сайте, не используется.
На четвертом этапе производится расчет координат вершин модели. Исходными данными для расчета являются значения параметров модели и то как мы представляем себе ее внешний вид. В файле pyramid_verts.js приведен исходный текст (с подробными комментариями) функции расчета вершин модели, которая имеет название VerticesCalculation. Именно при этом расчете в этой функции и используются функции библиотеки WebGeometry. Результаты расчета координат вершин заносятся в массив vertices. Заметим, что в программе нахождения координат вершин применяются отдельные последовательности номеров для вершин входящих в состав короны (четыре вершины), вершин входящих в состав рундиста (четыре вершины) и вершин входящих в состав павильона (в модели пирамида в состав павильона входит только вершина). Такой выбор дополнительной нумерации вершин применяется для более простой ориентации программистом среди вершин огранки, так как количество вершин очень часто превышает число 100.
На пятом этапе после того как расчет координат вершин закончен, требуется программно построить многогранник (полихедрон) модели. Исходными данными для его построения служат ранее созданные массивы index_cut, colors и vertices. Полихедрон модели можно представить просто как набор граней, которые ограничивают многогранник в пространстве. Функция CreatePolyhedron находится в файле polyhedron.js. В результате работы этой функции создается массив полигонов (многоугольников) из которых состоит трехмерная модель. Каждый полигон описывается следующей функцией (фактически это функция-конструктор вызываемая оператором new при создании нового полигона):
Так как WebGL и созданная на ее основе библиотека ThreeJS работает с треугольными примитивами, то для каждой грани модели производится ее триангуляция. При этом предполагается, что все грани модели представляют собой выпуклые многоугольники. В конечном итоге функция CreatePolyhedron производит все необходимые действия по созданию структур данных полностью описывающих все грани полихедрона в таком виде, что их можно передать функциям библиотеки ThreeJS для отображения модели на экране.
На шестом этапе производится отображение модели на экране посредством функций ThreeJS. Стандартным образом создается сцена, рендерер и камера. Для того, чтобы осмотреть модель огранки со всех сторон в программе Pyramid используется элемент orbitControls. При создании других моделей огранок, с целью осмотра огранок со всех сторон я использовал не orbitControls, а ввел возможность вращения самой модели. Затем мы создаем меши модели. Можно поступить двумя способами.
При первом способе мы рассматриваем модель огранки как набор отдельных мешей граней. В этом случае каждая грань представляет собой отдельный 3D объект. При таком представлении модели достаточно просто получается процесс выбора отдельной грани при помощи элемента Three.JS, который имеет название raycaster. Также этот способ можно дополнить созданием мешей отрезков, окаймляющих каждую грань.
При втором спосбе мы рассматриваем модель огранки как единый объект, представленный всего одним мешем включающим сразу все грани модели. Этот способ удобно использовать при отображении модели с помощью шейдеров. В модели огранки Pyramid этот способ не используется, но он применяется при создании моделей огранок Octagon, Brilliant и остальных, которые можно увидеть на моем сайте.
На седьмом этапе создаются кнопки и привязанные к ним функции, которые позволяют изменять значение параметров определяющих форму и размер модели. При нажатии кнопки вызывается функция которая производит увеличение или уменьшение значения соответсвующего параметра. Это означает, что необходимо пересчитать значение координат вершин модели. После пересчета проверяется корректность вновь построенной модели. Например определяется не выходят ли некоторые значения из допустимых пределов. В случае моделей огранок алмазов обычно это сводится к проверке того, осталась ли выпуклой огранка после ее перестроения. Проверка выпуклости производится следующим образом. Через каждую грань проводится плоскость, в которой эта грань лежит, и затем определяется положение каждой вершины модели относительно этой плоскости. Все вершины должны быть расположены по одну и ту же сторону от этой плоскости. Если модель признана некорректной, то производится возвращение к исходному значению измененного параметра и модель снова перестраивается. Для моделей огранок имеющих невыпуклый рундист (только этот элемент некоторых огранок, таких как Heart, может быть невыпуклым) проверка выпуклости производится отдельно для короны и отдельно для павильона. Рундист, при этом, исключается из проверки. Для простых моделей можно ограничиться простой проверкой параметра. Например, если мы конструируем модель дома, то крыша не должна быть по высоте больше некоторого, наперед заданного, значения. Поэтому просто задав ограничение этого параметра по величине, мы получим требуемый результат. После того как добавлены кнопки параметров очень желательно произвести визуальное отображение значения каждого параметра при его изменении после нажатия на кнопку. Для этого создается двумерный холст (canvas) HTML5 и рядом с соответствующей кнопкой на него выводится значение параметра.
Таким образом мы рассмотрели все этапы построения модели на примере Pyramid. Для пирамиды (впрочем, как и для всех остальных моделей на сайте) мной создана еще одна программа Pyramid_text.html. На примере этой программы показано как можно выводить трехмерный текст для нумерации вершин модели. Если кто-то захочет узнать как строятся сложные модели, то следует рассмотреть построение моделей (смотри GitHub) в следующей последовательности:
Octagon. Модель в которой демонстрируется создание плоскостей различными способами и работа с этими плоскостями. При построении модели также используются методы используемые при работе с векторами и прямыми в пространстве.
Brilliant. Это классическая и наиболее распространенная огранка алмазов. Некоторые элементы построения трехмерной модели этой огранки применяются в дальнейшем при создании огранок MoonMarquise, MoonPear и Heart. Как рассчитывается рундист этой огранки, имеющей форму суперэллипса, показано отдельно в программе BrilliantGirdlt.html. В этой программе линия рундиста строится на двумерном холсте (canvas).
MoonMarquise. Огранка типа Marquise, также как и Brilliant, является одной из классических огранок алмазов. В отличие от простой огранки этого типа (Marquise) в огранку MoonMarquise на павильон добавлены так называемые “лунные” грани (moon facets). Рундист огранки МoonMarquise образован двумя дугами эллипсами. Подробное построение этого рундиста на холсте показано в программе MarquiseGirdle.html. В тексте этой программы есть подробные комментарии к построению. Отметим один момент касающийся расчета линии рундиста – в нем используется свойство касательной к эллипсу. Оно рассматривается, например, в книге «Курс аналитической геометрии» (автор этой книги — Н.И.Мусхелишвили).
MoonPear. Рундист огранки МoonPear образован дугами трех эллипсов. Его построение основано на построении рундиста огранки Marquise, но является более сложным. Увидеть линию рундиста Marquise и способ разделения рундиста на сегменты, можно запустив программу PearGirdle.html.
Heart. Огранка “сердце” является одной из классических огранок, но она имеет, в отличие от большинства типов огранок, невыпуклую форму рундиста. Рудист огранки сердца составлен из двух наклоненных относительно друг друга рундистов огранок Pear. На холсте можно увидеть линию рундиста запустив программу HeartGirdle.html. Построение огранки Heart представляет собой достаточно сложную задачу.
Maltese Cross. Рундист огранки “Мальтийский крест” выполнен в форме “подушки” (cushion). Огранки с таким рундистом получили в последнее время широкое распространение. Линия этого рундиста представляет собой восемь сопряженных дуг окружностей – четыре основные дуги окаймляющие подушку с четырех сторон и четыре дуги меньшего размера производящие сопряжение основных дуг подушки по углам рундиста. Запустив программы CushionGirdle_1.html и CushionGirdle_2.html можно увидеть форму линии рундиста, работу всех параметров задающих его форму и деление рундиста на сегменты.
Pentagonal Star. Рундист огранки “Пятиугольная звезда” образован линией носящий название эпитрохоида. Эпитрохоида является кривой родственной циклоиде. В программе Wavy_Pentagon_Girdle.html путем изменения значений параметров можно изменить “волнистость” рундиста и даже изменить пятиугольник на многоугольник с другим количеством выступов (“лепестков”). Следует однако помнить, что сама модель этой огранки построена для значения параметра “Number of petals” равным 5.
Как уже упоминалось ранее, для всех вышеупомянутых моделей созданы программы отображающие номера вершин огранок. В этих программах сделано переключение между сквозной индикацией всех вершин модели и индикацией номеров вершин для короны, рундиста и павильона по отдельности. Предположим, что в модели огранки Maltese требуется создать плоскость проходящую через вершины имеющие номера 84, 88 и 145. Вместо того, чтобы при создании плоскости при помощи функции CreatePlaneThreePoints использовать эти номера для идентификации точек через которые проходит плоскость, гораздо более наглядной является запись использующая отдельную нумерацию вершин для рундиста и павильона:
Следует заметить, что программы отображающие номера вершин моделей работают весьма медленно (по крайней мере на моем компьютере). Может пройти несколько секунд прежде чем вывод номеров вершин модели будет закончен.
Подводя итог всему сказанному выше, по моему мнению, выбор многогранников (моделей огранок) для демонстрации работы геометрических функций, является одним из лучших вариантов. Разобрав работу вышеприведенных примеров, можно перейти к созданию геометрических объектов относящихся к совершено иным областям деятельности, чем моделирование огранок алмазов.

Для отображения моделей, предварительно рассчитанных с помощью функций из библиотеки WebGeometry, применяется библиотека ThreeJS. Холст (canvas) HTML5 используется для показа отдельных плоских элементов моделей и вывода на экран вспомогательной информации.
Технология WebGL и библиотеки созданные на ее основе, такие как ThreeJS и BadylonJS, используются в интернете для реализации самых разных целей, связанных с 3D графикой. Но в основном они находят применение для отображения в браузере уже готовых трехмерных моделей (предварительно созданных, например, в программах 3ds Max или Blender). Если перед нами встает задача создания параметрической модели, то есть такой модели, у которой, в процессе отображения в браузере уже готового объекта, мы можем изменить его отдельные элементы при помощи задания соответствующих параметров модели (например увеличить угол наклона некоторой грани), нам необходимо иметь набор геометрических функций, которые позволят создать модель таким образом, чтобы в дальнейшем существовала возможность интерактивно варьировать форму отдельных элементов модели или в целом всей модели. Для решения этой задачи нам потребуется набор функций на языке Javascript, которые будут реализовывать методы применяемые в аналитической геометрии. В библиотеке должны присутствовать функции для создания прямых, плоскостей и окружностей, нахождения точек (или прямых) пересечения их между собой, создания наклонных плоскостей и многое другое. В библиотеках ThreeJS и BadylonJS некоторые из этих возможностей присутствуют, но количество осуществляемых с помощью них действий не позволит выполнить все возникающие задачи при построении параметрической модели. Существуют еще несколько чисто математических Javascript библиотек. Из них наиболее широкое распространение получили glMatrix и Sylvester. Библиотека glMatrix в основном предназначена для работы с векторами, матрицами и кватернионами, но функций для работы с прямыми и плоскостями в ней нет. В библиотеке Sylvester эти функции есть, но присутствуют они в достаточно ограниченном количестве. Однако существует несколько книг в которых описана реализация методов аналитической геометрии на языке C/C++. Соответствующие программы на C/C++ можно использовать как прототипы при создании математической библиотеки на Javascript. Поэтому, когда я решил создать трехмерные параметрические модели огранок алмазов для отображения их в браузере, библиотека ThreeJS была выбрана мной только для вывода на экран уже рассчитанных моделей — для расчета формы моделей она не использовалась. Для самого расчета формы была создана библиотека WebGeometry. За основу этой библиотеки были взяты ранее использованные мной геометрические функции на C/C++, которые я перевел на язык Javascript. Рассмотрим этапы построения модели пирамиды (огранка алмаза типа Pyramid).
На первом этапе нам надо нарисовать предполагаемый вид модели и затем пронумеровать ее вершины. На приведенном рисунке приведена нумерация вершин и названия элементов огранки входящих в состав модели огранки пирамиды.

После этого требуется из пронумерованных вершин образовать грани. Например для грани площадки и граней короны следует записать следующую последовательность вершин (дублированная первая вершина грани сигнализирует о том, что грань закончилась):
0, 3, 2, 1, 0; // грань 0 - площадка
0, 4, 7, 3, 0, // грань 1 - корона
1, 5, 4, 0, 1, // грань 2 - корона
2, 6, 5, 1, 2, // грань 3 - корона
3, 7, 6, 2, 3, // грань 4 - корона
Обход граней следует производить против часовой стрелки. В файле pyramid_index.js приведен исходный текст обхода всех граней пирамиды и подробные комментарии. Результат обхода записывается в массив index_cut.
На втором этапе мы можем раскрасить грани модели. Этот этап не является обязательным, если раскраска нам не нужна. Предположим, что мы хотим раскрасить модель пирамиды следующим образом:

С этой целью создается файл pyramid_colors.js в котором находится функция facet_colors() которая осуществляет запись цветов всех граней в массив colors.
На третьем этапе, после того как пронумерованы все вершины и записаны последовательности обхода всех вершин граней, необходимо задать параметры модели и затем произвести расчет координат всех ее вершин. Конечно, предполагается что мы уже наметили для себя алгоритм построения и придумали как будут расположены в пространстве все грани модели. Для пирамиды мы выберем следующие параметры, которые будут задавать размеры как отдельных ее частей, так и всей модели в целом:
var DEGREE = 0.01745329251994; // величина углового градуса в радианах
var lw = 1.2; // отношение длина/ширина модели
var r = 0.06; // высота рундиста модели огранки
var angleA = 50*DEGREE; // угол наклона грани A короны
var angleB = 60*DEGREE; // угол наклона грани B короны
var hCrown = 0.3; // высота короны
var anglePav = 60*DEGREE; // угол наклона грани A павильона
Выбор параметров определяется разработчиком модели. Например, вместо задания двух параметров для двух углов наклона короны, можно задавать единственный параметр сразу для двух углов – тогда эти углы всегда будут одинаковыми. Можно ввести параметр определяющий размер площадки. В этом случае требуется либо не задавать высоту короны, либо не задавать наклон ее граней. Еще один вариант выбора параметров состоит в том, чтобы некоторые параметры сделать вычисляемыми. В этом случае при изменении одних параметров некоторые другие могут менять свое первоначальное значение. Например, если предположить, что для пирамиды мы определили один параметр для задания угла наклона граней короны, другой параметр для высоты короны и и еще один параметр, который будет задавать размер площадки, то при изменении наклона граней мы будем вынуждены изменять либо размер площадки, либо высоту короны. С другой стороны, если изменить параметр задающий размер площадки, то автоматически изменится значение параметра задающего либо высоту, либо наклон граней короны. Вариант связанный с применением вычисляемых параметров в данной программе, а также и при построении остальных моделей огранок, приведенных на сайте, не используется.
На четвертом этапе производится расчет координат вершин модели. Исходными данными для расчета являются значения параметров модели и то как мы представляем себе ее внешний вид. В файле pyramid_verts.js приведен исходный текст (с подробными комментариями) функции расчета вершин модели, которая имеет название VerticesCalculation. Именно при этом расчете в этой функции и используются функции библиотеки WebGeometry. Результаты расчета координат вершин заносятся в массив vertices. Заметим, что в программе нахождения координат вершин применяются отдельные последовательности номеров для вершин входящих в состав короны (четыре вершины), вершин входящих в состав рундиста (четыре вершины) и вершин входящих в состав павильона (в модели пирамида в состав павильона входит только вершина). Такой выбор дополнительной нумерации вершин применяется для более простой ориентации программистом среди вершин огранки, так как количество вершин очень часто превышает число 100.
На пятом этапе после того как расчет координат вершин закончен, требуется программно построить многогранник (полихедрон) модели. Исходными данными для его построения служат ранее созданные массивы index_cut, colors и vertices. Полихедрон модели можно представить просто как набор граней, которые ограничивают многогранник в пространстве. Функция CreatePolyhedron находится в файле polyhedron.js. В результате работы этой функции создается массив полигонов (многоугольников) из которых состоит трехмерная модель. Каждый полигон описывается следующей функцией (фактически это функция-конструктор вызываемая оператором new при создании нового полигона):
function Polygon()
{
this.IndexFacet = []; // индексы вершин грани без дублированной
// первой вершиной грани
this.IndexFacet_1 = []; // индексы вершин грани с дублированной
// первой вершиной грани
this.VertexFacet; // массив, содержащий координаты каждой
// вершины данной грани
this.EdgeFacet = []; // массив, содержащий индексы,
// определяющие ребро грани (каждый элемент массива содержит
//два индекса вершин)
this.IndexTriangle = []; // массив, содержащий индексы каждого
// треугольника, из которых состоит грань
this.VertexTriangle = []; // массив, содержащий координаты каждой
// вершины каждого треугольника, из которых состоит грань
this.Faces = []; // смотри комментарий в тексте программы
}
Так как WebGL и созданная на ее основе библиотека ThreeJS работает с треугольными примитивами, то для каждой грани модели производится ее триангуляция. При этом предполагается, что все грани модели представляют собой выпуклые многоугольники. В конечном итоге функция CreatePolyhedron производит все необходимые действия по созданию структур данных полностью описывающих все грани полихедрона в таком виде, что их можно передать функциям библиотеки ThreeJS для отображения модели на экране.
На шестом этапе производится отображение модели на экране посредством функций ThreeJS. Стандартным образом создается сцена, рендерер и камера. Для того, чтобы осмотреть модель огранки со всех сторон в программе Pyramid используется элемент orbitControls. При создании других моделей огранок, с целью осмотра огранок со всех сторон я использовал не orbitControls, а ввел возможность вращения самой модели. Затем мы создаем меши модели. Можно поступить двумя способами.
При первом способе мы рассматриваем модель огранки как набор отдельных мешей граней. В этом случае каждая грань представляет собой отдельный 3D объект. При таком представлении модели достаточно просто получается процесс выбора отдельной грани при помощи элемента Three.JS, который имеет название raycaster. Также этот способ можно дополнить созданием мешей отрезков, окаймляющих каждую грань.
При втором спосбе мы рассматриваем модель огранки как единый объект, представленный всего одним мешем включающим сразу все грани модели. Этот способ удобно использовать при отображении модели с помощью шейдеров. В модели огранки Pyramid этот способ не используется, но он применяется при создании моделей огранок Octagon, Brilliant и остальных, которые можно увидеть на моем сайте.
На седьмом этапе создаются кнопки и привязанные к ним функции, которые позволяют изменять значение параметров определяющих форму и размер модели. При нажатии кнопки вызывается функция которая производит увеличение или уменьшение значения соответсвующего параметра. Это означает, что необходимо пересчитать значение координат вершин модели. После пересчета проверяется корректность вновь построенной модели. Например определяется не выходят ли некоторые значения из допустимых пределов. В случае моделей огранок алмазов обычно это сводится к проверке того, осталась ли выпуклой огранка после ее перестроения. Проверка выпуклости производится следующим образом. Через каждую грань проводится плоскость, в которой эта грань лежит, и затем определяется положение каждой вершины модели относительно этой плоскости. Все вершины должны быть расположены по одну и ту же сторону от этой плоскости. Если модель признана некорректной, то производится возвращение к исходному значению измененного параметра и модель снова перестраивается. Для моделей огранок имеющих невыпуклый рундист (только этот элемент некоторых огранок, таких как Heart, может быть невыпуклым) проверка выпуклости производится отдельно для короны и отдельно для павильона. Рундист, при этом, исключается из проверки. Для простых моделей можно ограничиться простой проверкой параметра. Например, если мы конструируем модель дома, то крыша не должна быть по высоте больше некоторого, наперед заданного, значения. Поэтому просто задав ограничение этого параметра по величине, мы получим требуемый результат. После того как добавлены кнопки параметров очень желательно произвести визуальное отображение значения каждого параметра при его изменении после нажатия на кнопку. Для этого создается двумерный холст (canvas) HTML5 и рядом с соответствующей кнопкой на него выводится значение параметра.
Таким образом мы рассмотрели все этапы построения модели на примере Pyramid. Для пирамиды (впрочем, как и для всех остальных моделей на сайте) мной создана еще одна программа Pyramid_text.html. На примере этой программы показано как можно выводить трехмерный текст для нумерации вершин модели. Если кто-то захочет узнать как строятся сложные модели, то следует рассмотреть построение моделей (смотри GitHub) в следующей последовательности:
Octagon. Модель в которой демонстрируется создание плоскостей различными способами и работа с этими плоскостями. При построении модели также используются методы используемые при работе с векторами и прямыми в пространстве.
Brilliant. Это классическая и наиболее распространенная огранка алмазов. Некоторые элементы построения трехмерной модели этой огранки применяются в дальнейшем при создании огранок MoonMarquise, MoonPear и Heart. Как рассчитывается рундист этой огранки, имеющей форму суперэллипса, показано отдельно в программе BrilliantGirdlt.html. В этой программе линия рундиста строится на двумерном холсте (canvas).
MoonMarquise. Огранка типа Marquise, также как и Brilliant, является одной из классических огранок алмазов. В отличие от простой огранки этого типа (Marquise) в огранку MoonMarquise на павильон добавлены так называемые “лунные” грани (moon facets). Рундист огранки МoonMarquise образован двумя дугами эллипсами. Подробное построение этого рундиста на холсте показано в программе MarquiseGirdle.html. В тексте этой программы есть подробные комментарии к построению. Отметим один момент касающийся расчета линии рундиста – в нем используется свойство касательной к эллипсу. Оно рассматривается, например, в книге «Курс аналитической геометрии» (автор этой книги — Н.И.Мусхелишвили).
MoonPear. Рундист огранки МoonPear образован дугами трех эллипсов. Его построение основано на построении рундиста огранки Marquise, но является более сложным. Увидеть линию рундиста Marquise и способ разделения рундиста на сегменты, можно запустив программу PearGirdle.html.
Heart. Огранка “сердце” является одной из классических огранок, но она имеет, в отличие от большинства типов огранок, невыпуклую форму рундиста. Рудист огранки сердца составлен из двух наклоненных относительно друг друга рундистов огранок Pear. На холсте можно увидеть линию рундиста запустив программу HeartGirdle.html. Построение огранки Heart представляет собой достаточно сложную задачу.
Maltese Cross. Рундист огранки “Мальтийский крест” выполнен в форме “подушки” (cushion). Огранки с таким рундистом получили в последнее время широкое распространение. Линия этого рундиста представляет собой восемь сопряженных дуг окружностей – четыре основные дуги окаймляющие подушку с четырех сторон и четыре дуги меньшего размера производящие сопряжение основных дуг подушки по углам рундиста. Запустив программы CushionGirdle_1.html и CushionGirdle_2.html можно увидеть форму линии рундиста, работу всех параметров задающих его форму и деление рундиста на сегменты.
Pentagonal Star. Рундист огранки “Пятиугольная звезда” образован линией носящий название эпитрохоида. Эпитрохоида является кривой родственной циклоиде. В программе Wavy_Pentagon_Girdle.html путем изменения значений параметров можно изменить “волнистость” рундиста и даже изменить пятиугольник на многоугольник с другим количеством выступов (“лепестков”). Следует однако помнить, что сама модель этой огранки построена для значения параметра “Number of petals” равным 5.
Как уже упоминалось ранее, для всех вышеупомянутых моделей созданы программы отображающие номера вершин огранок. В этих программах сделано переключение между сквозной индикацией всех вершин модели и индикацией номеров вершин для короны, рундиста и павильона по отдельности. Предположим, что в модели огранки Maltese требуется создать плоскость проходящую через вершины имеющие номера 84, 88 и 145. Вместо того, чтобы при создании плоскости при помощи функции CreatePlaneThreePoints использовать эти номера для идентификации точек через которые проходит плоскость, гораздо более наглядной является запись использующая отдельную нумерацию вершин для рундиста и павильона:
var plane = new Plane3D();
plane.CreatePlaneThreePoints(girdle[68], girdle[72], crown[1]);
Следует заметить, что программы отображающие номера вершин моделей работают весьма медленно (по крайней мере на моем компьютере). Может пройти несколько секунд прежде чем вывод номеров вершин модели будет закончен.
Подводя итог всему сказанному выше, по моему мнению, выбор многогранников (моделей огранок) для демонстрации работы геометрических функций, является одним из лучших вариантов. Разобрав работу вышеприведенных примеров, можно перейти к созданию геометрических объектов относящихся к совершено иным областям деятельности, чем моделирование огранок алмазов.


alexkowel
Хорошая статья, спасибо большое!