В 1921 году Отто Штерн приехал в город Франкфурт, где познакомился в уроженцем этого города и сотрудником местного университета Вальтером Герлахом, вместе с которым они в том же году и провели прославивший их опыт. Впоследствии выяснилось, что почти всю математику описывающую, спин отдельного электрона, можно вывести из этого эксперимента. Читая описание эксперимента, такой вывод совершенно не кажется очевидным. Хотя бы, например, с какой стати в математике спина электрона появляются комплексные числа?

Чтобы прояснить связь математики спина с экспериментом Штерна‑Герлаха (Ш‑Г) мной была сделана его программная модель. При описании спина электрона очень часто используется сфера Блоха. В программной модели эксперимент Ш‑Г, можно сказать, был совмещен со сферой Блоха. При таком подходе можно визуально увидеть геометрию некоторых соотношений описывающих спин электрона. Увидеть несколько интерактивных программ можно в браузере на сайте Bloch sphere online.

При создании данного сайта использовалась главным образом школьная математика. В основном тригонометрия и простейшие действия с комплексными числами, а также формула Эйлера. Также для понимания материала требуются первоначальные сведения о матрицах.

Как производится возведение числа в степень, когда в качестве показателя степени выступает матрица, рассматривается непосредственно в тексте на сайте.

При рассмотрении примеров из четвертой части требуется понимание того, чем являются собственные числа и собственные векторы. Но четвертая часть фактически является факультативным дополнением к первым трем частям и читать ее необязательно.

В первой части этого сайта подробно рассматривается программная модель эксперимента Ш‑Г. Трехмерная визуализация этого эксперимента сделана таким образом, чтобы из него совершенно естественным образом вытекала трехмерная визуализация сферы Блоха. Описание эксперимента Ш‑Г взято из книги Леонарда Сасскинда и Арта Фридмана «Квантовая механика». В этой книге эксперимент Ш‑Г производится при помощи объекта, который назван «прибором». Очень желательно одновременно с использованием программной модели из этой части читать первую лекцию указанной книги.

Однако визуально эксперимент Ш‑Г из программной модели имеет совершенно другой вид, чем тот, который приведен в книге. Для визуализации «прибора» из книги используется сфера. Сначала спин получает определенное направление (приготовление спина), которое задается на сфере вектором A. Затем задается направление вдоль которого будет производиться измерение спина при помощи вектора D (от слова Device — прибор). После этого производится сам процесс измерения и высвечиваются его результаты.

Во второй части сайта показано как из программной модели получаются основные формулы для расчета спина электрона. Для этой цели программная модель из первой части рассматривается немного под другим углом зрения. Теперь мы считаем, что спин всегда приготовлен вертикально вверх и поэтому вектор A на сфере уже не нужен. Измерение спина автоматически производится вдоль вектора, который в первой части назывался D. Но во второй части он получает стандартное название — вектор Блоха и обозначен он на сфере символом B.

Кроме того на сфере появляется вектор состояния |ψ>. Из визуализации мы видим, что одному обороту вектора состояния соответствуют два оборота вектора Блоха.

Вектор состояния |ψ> живет в двумерном пространстве, но реагирует на повороты в трехмерном пространстве. Из‑за такого его странного поведения пришлось ввести комплексное спинорное пространство. Во второй части я попытался наглядно (очень упрощенно и возможно не очень корректно) продемонстрировать появление комплексных чисел.

Также в этой части приведено несколько рисунков сделанных на основе визуализации, которые геометрически показывают как формируется вектор |ψ>.

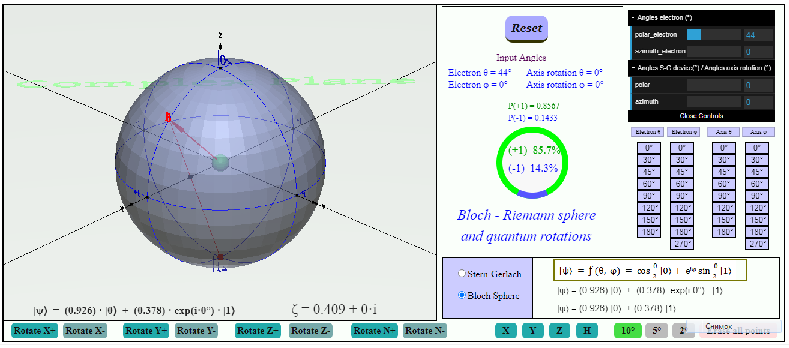
В третьей части сделана программная модель состоящая из двух отдельных программ, которые можно переключать между собой. Первая из них в основном повторяет программную модель из первой части. А вторая программа представляет собой модель сферы Блоха‑Римана. Эта вторая программа позволяет производить квантовые вращения на сфере Блоха и, заодно, показывает представление этих вращений на обычной комплексной плоскости. Переключение между двумя программами позволяет лучше понять глубокую связь эксперимента Ш‑Г со сферой Блоха. Именно для подчеркивания преемственности между экспериментом Ш‑Г и сферой Блоха и введена еще раз первая из двух программ — эксперимент Ш‑Г.

Заметим, что в программной модели, приведенной в первой части, показан только эксперимент Ш‑Г и заблокирован переход к сфере Блоха. В третьей части переход к сфере Блоха разблокирован. Поэтому в ней можно последовательно проводить и эксперимент Ш‑Г и осуществлять квантовые вращения на сфере Блоха. Переход от визуализации эксперимента Ш‑Г к визуализации сферы Блоха можно осуществить при помощи переключателя.

В третьей части особое внимание уделено визуализации квантовых вращений. Квантовые вращения имеют особую важность так как каждому вращению спина можно сопоставить однокубитный квантовый вентиль и наоборот каждому квантовому вращению соответствует квантовый вентиль. Понимание механизма квантовых вращений помогает понять основу квантовых вычислений.

В программе реализована возможность проводить вращения вокруг осей X, Y и Z. Вращение также можно произвести в пространстве и вокруг предварительно заданной произвольной оси.

Также в программе можно наблюдать действие трех матриц Паули и матрицы Адамара.

На мой взгляд особый интерес представляет отображение вращений на комплексную плоскость. Такие отображения описывает в нескольких своих книгах Роджер Пенроуз.

В четвертой части приведены решения упражнений 3.3, 3.4 и 3.5 из книги Леонарда Сасскинда и Арта Фридмана «Квантовая механика». Решения данных упражнений не приведено в их книге. Но весьма не сложная математика используемая при решении этих упражнений позволяет лучше понять суть собственных значений и собственных векторов при описании квантового спина.

Материал данного сайта во многом заимствован из моей предыдущей работы. В настоящем сайте исправлены некоторые ошибки и добавлены новые возможности программ. Особенно это касается четвертой части. В программе этой части введено квантовое онлайн вращение вокруг произвольной оси в браузере. Программы с такой возможностью в интернете мне не попадалась

На github можно посмотреть некоторые мои работы.