
Факториал натурального числа определяется так:
. Например,
- число со 157 цифрами.
равно числу способов переставить
элементов между собой. Для оценки
используют формулу Стирлинга:
Обратим внимание, что эта формула содержит числа и
и возникла из очень простой модели с перестановками.
Посмотрим, как она работает, на примерах
Возьмём среднее арифметическое первых
натуральных чисел. Легко видеть (геометрически и алгебраически), что
, середина отрезка натурального ряда
. Как ведёт себя среднее геометрическое
первых
натуральных чисел? С помощью формулы Стирлинга легко установить:
Что довольно намного меньше . Попробуйте понять как ведёт себя среднее гармоническое первых
натуральных чисел. Кстати, среднее геометрическое произведения случайных чисел, выбранных независимо и равномерно на отрезке
также стремится к числу
с ростом числа множителей.
Рассмотрим следующую вероятностную задачу. Пусть у нас есть симметричных монет. Подкинем их все. С какой вероятностью
орлов выпадет столько же, сколько и решек?
Эта вероятность равна . При больших
можно применить формулу Стирлинга и получить
Это значит, что такая вероятность при броске 40 монет будет примерно вдвое меньше, чем при броске 10 монет.
Также это даёт нам способ вычислить число в домашних условиях (если у вас есть достаточно большое количество монет): возьмём 100 монет и повторим наш эксперимент 10000 раз. Посчитаем, в скольких экспериментах орлов выпало столько же, сколько и решек.
Пусть это число равно .
Тогда из сказанного выше вытекает:
Остаётся вопрос о точности такого приближения. Но это совсем другая история, связанная с центральной предельной теоремой.
Пишите в комментариях какие вы знаете применения формулы Стирлинга.
Авторы:
Лыков Александр, научный сотрудник мехмата МГУ, академический руководитель ШАД Хелпера
Михаил Михеенко, студент пятого курса мехмата МГУ, куратор ШАД Хелпера.
Комментарии (15)

Fodin
00.00.0000 00:00+21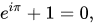
Эта, вроде, тоже неплохо соединяет. 
alexlyk314 Автор
00.00.0000 00:00+1Прекрасная формула Эйлера заслуживает отдельной статьи

runaway
00.00.0000 00:00+1Формула Эйлера соединяет в себе:
арифметику (1);
алгебру (e);
геометрию (pi);
матан (i).
Это самая красивая формула математики.

ftpgg
00.00.0000 00:00+1Не, всё-таки очень странно вы их обозвали
Этот частный случай формулы Эйлера
, объединяющий 5 фундаментальных математических констант. Разделение на алгебру, геометрию, арифметику и откуда-то взявшийся математический анализ не особо уместно, как минимум из-за вездесущности их друг у друга)

Refridgerator
00.00.0000 00:00* Это самая красивая формула для тех, кто не понимает её смысла. Потому что (сюрприз) при её вычислении ни е, ни пи не используются. е здесь — это показательная функция, а не константа, и если сменить её основание на менее пафосное и более пригодное для практических вычислений, например -1, то тождество примет вид
, ну то есть 1-1=0, тоже мне магия. Заодно понятно надеюсь, как в одной формуле объединить произвольное количество констант и придать им немного магии, например:
пояснениеШутка о том, что в военное время значение синуса может достигать четырех никакая не шутка.

belch84
00.00.0000 00:00+7Есть еще такая формула, связывающая e и pi:
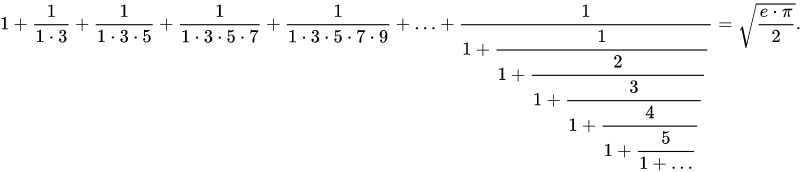
, открытая Рамануджаном (здесь сумма ряда и цепной дроби)
codecity
00.00.0000 00:00+5Не открытая а данная ему в дар богиней Намагири Тхайяр. Если человек так говорил - почему мы должны ему не верить?

belch84
00.00.0000 00:00-2Какая разница, как он получил формулу? Да, богиня во сне подсказала, но доказательство же он сам выполнил

codecity
00.00.0000 00:00+1Вроде никаких доказательств он не выполнял, по крайней мере для большинства выводимых им замечательных формул.

belch84
00.00.0000 00:00+2Мне трудно спорить, но, вроде бы, в этом случае доказательство было, для выяснения нужно заглянуть в Journal of the Indian Mathematical Society, vol.VIII, January, 1916, стр.17-20, такой возможности у меня нет.
Информация взята из http://www.ega-math.narod.ru/Rama/Rama1.htm

Refridgerator
00.00.0000 00:00Такие тождества не получаются через божественное явления, а мышление в фоновом режиме во время сна вполне нормальное явление. Такие тождества делаются по одному и тому же методу:
1) сначала берётся функция, которая с определённым аргументом даёт нужное значение;
2) затем эта функция раскладывается в ряды, дроби, другие функции т.д.;
3) затем меняем аргумент на конкретное число, меняем местами причину и следствие и вуаля — магия готова.

belch84
00.00.0000 00:00Не смог удержаться и построил график, на котором сравниваются частичные суммы ряда, сложенные с соответствующими приближенными значениями цепной дроби, и константа из формулы
Иллюстрация к формуле РамануджанаЗеленый график-частичные суммы ряда, голубой-последовательные приближения для цепной дроби, красный-их сумма, желтый — константа из формулы
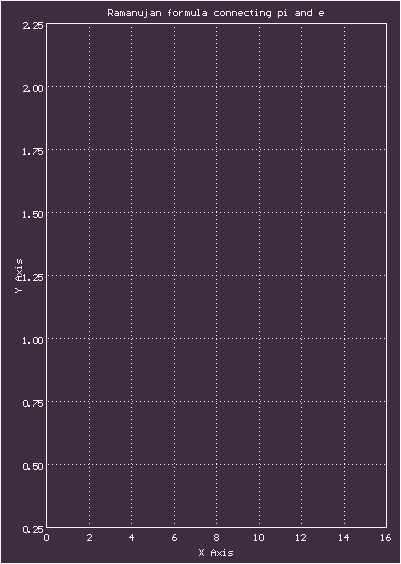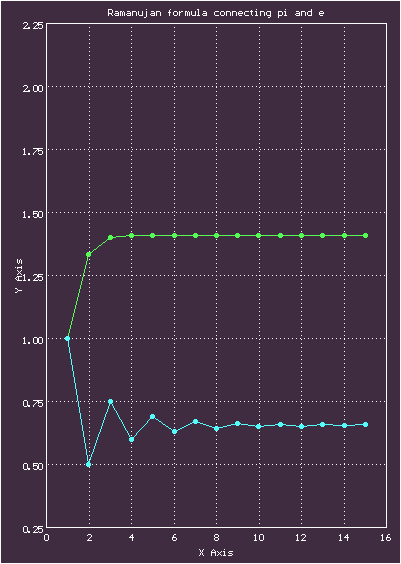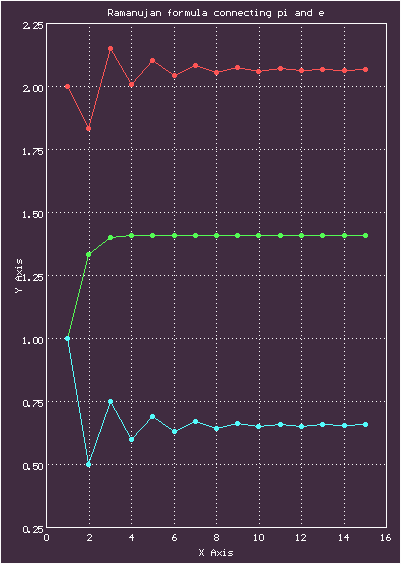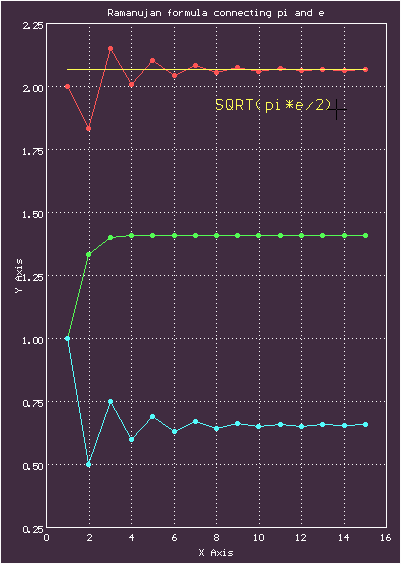
Здесь взято 15 членов ряда, видно, что сходимость довольно быстрая

yurixi
00.00.0000 00:00+4Статья на два абзаца. В первом рассказывают что такое факториал и говорят о том что Стирлинг — клёвый мужик, умеет подсказывать значения факториала, пускай и не точно. Тут же идёт удивление, что среди его подсказок неизвестно почему встречается число пи и е. Ну прикольно же? Стоит сменить название на «как я однажды удивился формуле стрилинга». И содержание надо было оставить три слова «сразу как увидел».
А, там же ещё второй абзац. С помощью монеток обнаруживается, что в четыре раза больше бросков в два раза меньше вероятность серединного результата и что число пи ну точно есть в этой формуле. Заканчивается упоминанием теоремы о которой рассказывать никто не собирался и туповатой фразой «ну а это другая история», как будто рассказана история и много таких историй ожидается и потом. А можно не надо? Рассказано ничего не было, просто пара рассуждений из ниоткуда в никуда. Впечатление — что вы сами не знаете о чём говорите. Ещё тупее — это просьба в комментариях на хабре писать применение формулы Стирлинга.
Зачем вы это опубликовали, признайтесь честно, вам угрожали? Мне за вас стыдно. У вас ещё и авторов два. Это что — с каждого по абзацу что ли? Или один другого заставил? Или это стенограмма скайп-конференции? А кто эти люди, которые это плюсуют? Школьники?
Вот я пишу статью по схожей теме, оттачиваю порядок рассуждений, беспокоюсь, чтобы всё что нужно знать в статье и упоминалось, и переживаю, что получилось слишком много текста. А тут, оказывается, напиши два абзаца комментариев в сторону и готова статья. Кроме того что это само по себе ни о чём, это сбивает уровень. Это вот такое дно теперь будет считаться новой нормой?
Я может, предвзятый, вплоть до того что каждого кто любуется формулой эйлера записываю в гуманитарии, тех кто вычисляет число пи с помощью монеток и иголок — сразу в идиоты, но… то как надо писать статьи — вот где для вас «а это совсем другая история, которую я не читал».



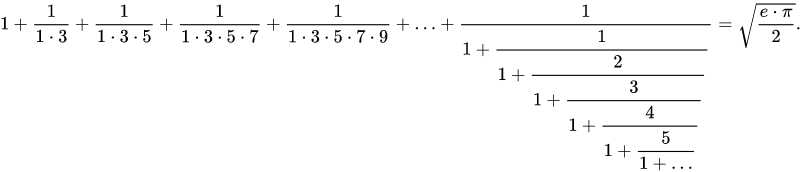
OBIEESupport
Уважаемый автор! С одной стороны - все предельно просто, с другой - из этого построен весь материал ШАД. Может быть, глянете мои вариации на эту же тему?