Всем привет! Меня зовут Рома Смирнов. Я работаю продуктовым аналитиком в Lamoda Tech. Не так давно я столкнулся с необычным взглядом на то, как следует интерпретировать результаты A/B-эксперимента. Он заключается в том, что наблюдаемый аплифт — разницу средних, полученную на основе выборок, — необходимо сравнивать не только с критическим z- или t-значением, но еще и с MDE, минимальным эффектом, который мы ожидаем зафиксировать. Утверждается, что тест следует принимать только в том случае, если наблюдаемый аплифт лежит правее значения MDE.

Кажется, что на занятиях по статистике такому обычно не учат. Я обратился к традиционному источнику информации — Всемирной паутине (web, internet) — и нашел на эту тему хорошую статью болгарского гигачада A/B-тестирования Георгия Георгиева. В ней он приводит несколько аргументов, демонстрирующих несостоятельность описанного выше подхода.

В своей статье я буду использовать аргументы Георгия Георгиева, разбавленные моими мыслями и примерами на эту тему.

Формула мощности

Она же формула для определения размера выборки:

• — размер выборки для каждой из двух групп теста.

• — дисперсия группы i.

• — значения стандартного нормального распределения, соответствующие заданным уровням значимости и мощности.

Давайте отдельно обсудим, что такое MDE.

Когда мы проводим эксперимент, мы говорим о том, что у нас есть нулевая гипотеза H_0, предполагающая, что выборки из тестовой и контрольной групп взяты из одной и той же генеральной совокупности. Также мы выдвигаем альтернативную гипотезу H_a, предполагающую, что выборки из тестовой и контрольной групп взяты из разных генеральных совокупностей с разными математическими ожиданиями.

Истинное значение разницы математических ожиданий в случае, когда альтернативная гипотеза верна, мы не знаем. Но мы можем сделать предположение о том, какой эта разница может быть. Таким образом, мы получаем предполагаемый ожидаемый эффект. Если мы подставим его в формулу мощности в качестве MDE, то получим размер выборки, необходимый для того, чтобы зафиксировать этот предполагаемый эффект при условии, что вероятность ошибки первого рода будет равна alpha/2, а вероятность ошибки второго рода будет равна beta.

Это можно визуализировать следующим образом:

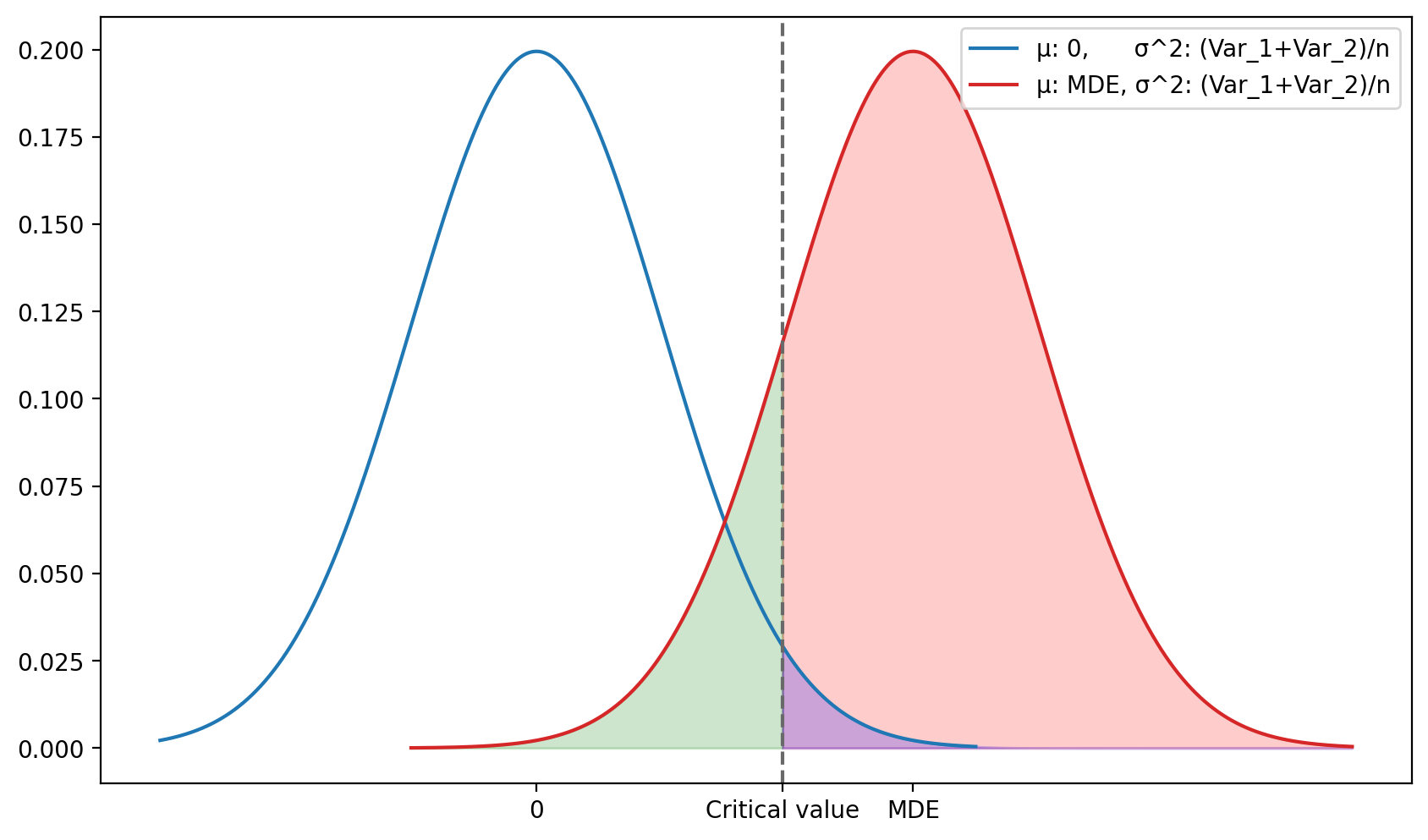
Вы могли обратить внимание на то, что в предыдущем абзаце я зачем-то выделил жирным шрифтом слова «при условии…». Сделал я это для того, чтобы обратить ваше внимание на то, что значение MDE не высечено в камне. Это лишь наше предположение о том, каким реальный эффект может быть.

Поэтому предлагаю ввести три понятия, которые важно различать:

• Реальный, или истинный эффект — это тот эффект, который в действительности оказала фича, которую мы тестируем. Этот эффект при проведении эксперимента мы не знаем.

• Предполагаемый эффект — это тот эффект, который мы подставляем в формулу мощности в качестве MDE, чтобы определить размер выборки. Он не равен реальному эффекту, а является лишь догадкой о том, каков реальный эффект на самом деле.

• Наблюдаемый аплифт — это разница средних выборки теста и выборки контроля.

Эфемерность MDE

Есть одна вещь, которая всегда смущала меня в формуле мощности. Она заключается в некой эфемерности понятий мощности и MDE в сравнении с понятиями размера выборки, уровня значимости и дисперсии.

Когда мы проводим эксперимент, мы можем «физически» наблюдать размер выборки — после окончания эксперимента это число остается неизменным на экране наших мониторов. Такой же неизменной является дисперсия в данных, посчитанная на предпериоде при планировании эксперимента. Критическое значение, которое мы определяем в том числе на основе уровня значимости, также «физически» используется для сравнения с наблюдаемым аплифтом.

А что с мощностью и MDE? Эти два параметра на самом деле нам неизвестны. Мы можем лишь подставлять один из них в формулу мощности, чтобы получить второй.

Например, мы провели эксперимент со следующими параметрами:

• n=1000

• Var = 30

• alpha/2 = 0.025

Подставим в формулу и получим следующее:

Вопрос: какую мощность теста нам следует репортить? Да, можно сказать, что следует репортить ту мощность теста и то значение MDE, которые мы использовали, чтобы понять, что нам нужно 1000 наблюдений. Но почему именно их? Почему бы нам при репортинге не увеличить пропорционально значение MDE и мощности, сказав, что мощность теста теперь, например, не 80%, а 90%? Ведь, как я уже сказал, реальный эффект мы не знаем и можем лишь гадать, каким он будет, подставляя разные значения MDE в формулу.

Эквивалентность двух заблуждений

Разграничив понятия реального эффекта, предполагаемого эффекта и наблюдаемого аплифта, а также поставив многоточие в вопросе эфемерности MDE, давайте перейдем непосредственно к тому взгляду на принятие экспериментов, с которого я начал статью.

Есть два эквивалентных правила, которые предлагается использовать при анализе результатов тестов:

1. Для того, чтобы принять эксперимент, недостаточно одного того факта, что p-value < alpha/2 (aka 0 не попадает в доверительный интервал). Необходимо также, чтобы наблюдаемый аплифт был больше, чем предполагаемый эффект, который использовался в качестве MDE при подсчете размера выборки.

2. Для того, чтобы принять эксперимент, недостаточно одного того факта, что p-value < alpha/2 (aka 0 не попадает в доверительный интервал). Необходимо также, чтобы мощность, выраженная через формулу мощности, в которую подставили наблюдаемый аплифт в качестве MDE, была больше, чем мощность, выраженная через формулу мощности, в которую подставили предполагаемый эффект в качестве MDE.

Эквивалентность формулировок довольно очевидна. В первом случае мы сравниваем наблюдаемый аплифт с предполагаемым эффектом as is. Во втором случае мы подставляем каждое из этих значений в одну и ту же формулу, выражаем мощность и сравниваем их.

Почему так делать не надо

Панч #1. Отсутствие в этом какого-либо смысла

Давайте представим, что мы рассчитываем размер выборки.

• Var = 90000

• alpha/2 = 0.025

• beta = 0.2

• power = 0.8

• Предполагаемый эффект = 2

Тогда размер выборки 290000(0.842+1.96)²/2² = 353304. Мы набираем 353304 наблюдений для каждой из групп, считаем средние и получаем наблюдаемый аплифт 1.78. Пусть этот аплифт выше, чем критическое значение t-/z-статистики. Предположим также, что дисперсия Var = 90000, которую мы посчитали на предпериоде, в точности равна дисперсии в период эксперимента.

По предлагаемой логике, нам следует подставить 1.78 в формулу вместо 2 и посчитать мощность. Если мы сделаем это, то получим значение мощности в районе 70%.

То есть получается, что мы планировали эксперимент, подставляли значения в формулу, считали размер выборки, исправно ждали, пока наберется нужное количество наблюдений, и почему-то все равно получили мощность ниже той, которую изначально закладывали.

Значит ли это, что формула мощности не работает? Нет. Просто подставлять аплифт в эту формулу не имеет смысла. Как только мы получили p-value меньше 0.025, нас вообще не должна волновать ошибка второго рода (а значит и мощность), так как она имеет дело с вероятностью не отвергнуть нулевую гипотезу в случае, если она неверна. То есть с ситуацией, когда p-value больше 0.025.

Не очень понятно, что вообще будет означать мощность, равная 70%. Если мощность — это вероятность зафиксировать статистически значимый эффект там, где он действительно есть, при заданных параметрах дисперсии, уровня значимости и MDE, то получается, что мы считаем эту вероятность, предполагая, что реальный эффект равен наблюдаемому аплифту. Но ведь вся инферентная статистика как раз про то, что наблюдаемые значения не равны истинным.

Панч #2. Игнорирование левой половины распределения

Если предыдущий аргумент показался слишком расплывчатым, предлагаю провести мысленный эксперимент.

Предположим, что альтернативная гипотеза точно верна. Это означает, что фича оказала какой-то реальный эффект. Пусть этот эффект будет равен 3. Следовательно, если мы будем много раз брать выборки одного и того же размера из теста и контроля и считать разницу средних, то мы получим нормальное распределение с математическим ожиданием равным 3.

Теперь предлагаю закрыть глаза и вспомнить, как выглядит нормальное распределение. Видите колокол? Если вы представили правильно, то колокол будет симметричным. А математическое ожидание будет лежать как раз в центре.

Что это означает? Это означает то, что разница средних, посчитанных на основе выборок, взятых из двух генеральных совокупностей с разницей математических ожиданий 3, может лежать как справа от 3, так и слева. Если мы будем принимать тест только в случае, если разница средних (наш наблюдаемый аплифт) лежит справа от 3, то реальная мощность (вероятность отвергнуть нулевую гипотезу там, где она неверна), начиная с определенного размера выборки, будет всегда равна 50%.

Давайте проверим это с помощью симуляций.

1. Зададим две генеральные совокупности с математическими ожиданиями 1000 и 1003 и дисперсиями, равными 90 000.

2. Возьмем alpha/2 = 0.025.

3. Будем подставлять разные значения мощности в формулу и определять размер выборки. В данном случае в качестве значения MDE мы будем брать не предполагаемый эффект, а реальный, так как мы его точно знаем.

4. Для каждого полученного значения n будем брать по 1000 выборок из заданных генеральных совокупностей и сравнивать средние с помощью t-теста. В функции t-теста будем сравнивать наблюдаемый аплифт как с критическим значением, так и с MDE. Если наблюдаемый аплифт будет больше обоих значений, то будем записывать результат как 1, в противном случае — как 0.

5. Для каждого значения n посчитаем процент 1 — эмпирическую мощность.

6. Сравним значения мощности, которые мы подставляли в формулу, с теми, которые мы получили на симуляциях.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as sps
from tqdm.notebook import tqdm as tqdm_notebook
from statsmodels.stats.proportion import proportion_confint
from scipy.stats import norm

def strange_ttest(sample_a, sample_b, z_sig, mde):
    
    mean_sample_a = np.mean(sample_a)
    mean_sample_b = np.mean(sample_b)
    diff_mean = mean_sample_b - mean_sample_a
    
    std_error_a = np.var(sample_a)/len(sample_a)
    std_error_b = np.var(sample_b)/len(sample_b)
    diff_mean_std_error = std_error_a + std_error_b
    t_stat = diff_mean/np.sqrt(diff_mean_std_error)
    
    if t_stat >= z_sig and diff_mean >= mde:
        res = 1
    else:
        res = 0
    return res

# Зададим исходные параметры
mean_a = 1000 
mean_b = 1003
var_a = 90000
var_b = 90000
mde = mean_b-mean_a # Реальный эффект
sig = 0.025
z_sig = sps.norm.ppf(1-sig)
N = 1000
theoretical_power = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.99]
real_power = []
left_real_power = []
right_real_power = []
sample_size = []

for power in tqdm_notebook(theoretical_power):
    
    results = []
    
    z_power = sps.norm.ppf(1-power)
    n = (var_a + var_b)*((z_sig - z_power)**2)/(mde**2)
    n = round(n)
    
    for i in tqdm_notebook(range(N)):

        sample_a = sps.norm(loc=mean_a, scale=np.sqrt(var_a)).rvs(n)
        sample_b = sps.norm(loc=mean_b, scale=np.sqrt(var_b)).rvs(n)
        res = strange_ttest(sample_a, sample_b, z_sig, mde)
        results.append(res)  
        
    empirical_power = np.mean(results)
    # считаем доверительный интервал для вероятности успеха серии испытаний Бернулли
    left_real_level, right_real_level = proportion_confint(count=N*empirical_power, 
                                                           nobs=N, 
                                                           alpha=0.05, 
                                                           method='wilson')
        
    real_power.append(empirical_power)
    left_real_power.append(left_real_level)
    right_real_power.append(right_real_level)
    sample_size.append(n)

Визуализируем результаты:

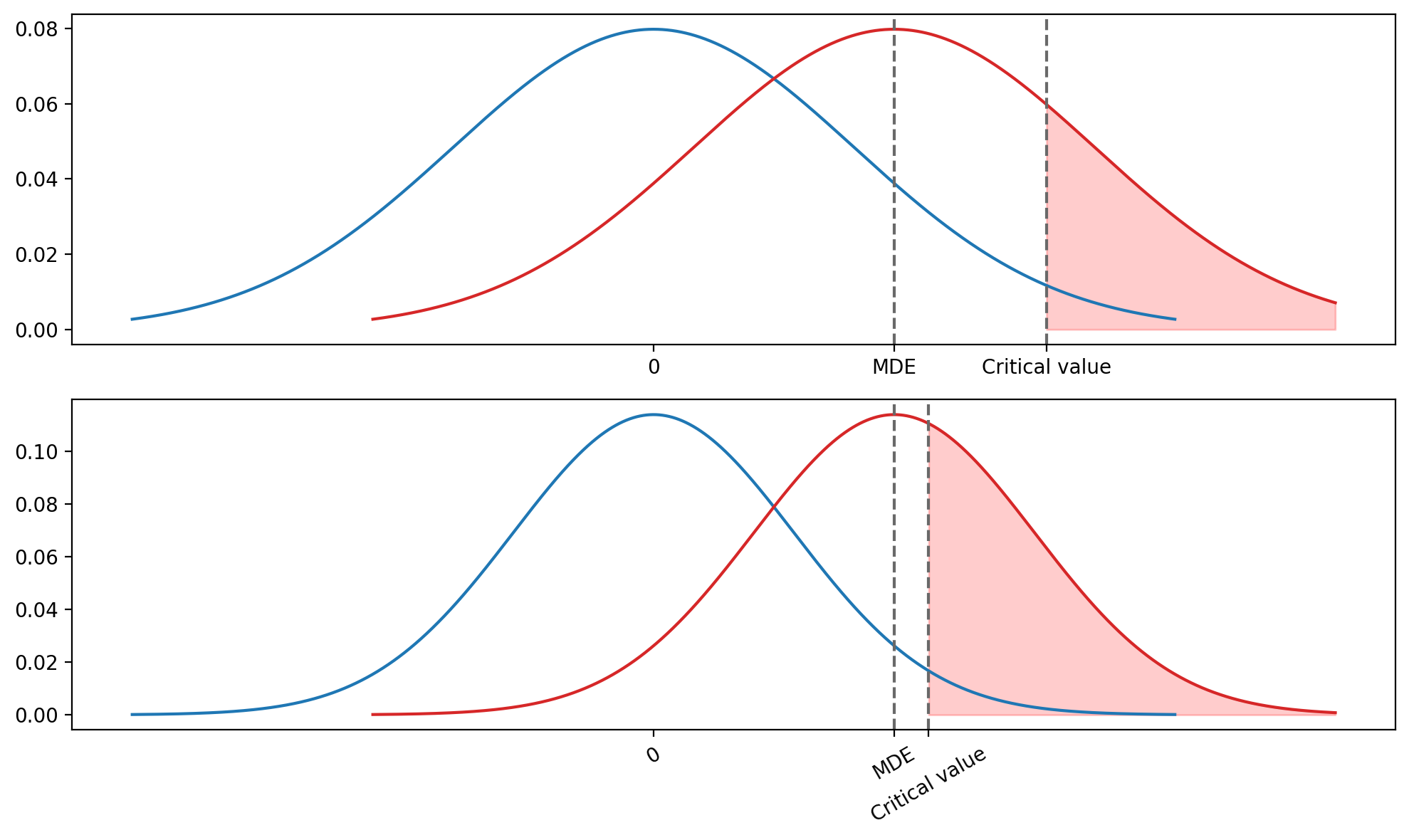
Как и ожидалось, начиная с 50%, мощность, полученная на симуляциях, перестает расти. Получается, как бы сильно мы не старались, мы все равно обнаруживаем статистическую значимость только в половине случаев. Возникает ситуация, когда мы используем некое абстрактное понятие мощности для расчета размера выборки, но в реальности ничего подобного не наблюдаем.

Почему так происходит? Проблема заключается в том, что мы, по сути, вводим дополнительный критерий принятия теста в виде MDE, тем самым делая в некоторых случаях тест намного более консервативным в плане принятия альтернативной гипотезы. В самом факте того, чтобы сделать тест более консервативным, нет ничего плохого. Однако это следует делать не таким экстравагантным способом, а за счет изменения уровня значимости, чтобы избегать выхода мощности на плато.

В случае, если значение мощности, которое мы подставляем в формулу, больше 50%, вертикальная линия, соответствующая критическому значению, будет лежать левее, чем MDE. Так как мы используем в качестве критерия max(Critical value, MDE), критерий принятия теста будет оставаться неизменным и равным MDE. Мы не будем наблюдать увеличения мощности, какого бы размера выборку не взяли, так как увеличение размера выборки будет влиять только на сдвиг критического значения относительно красного распределения. Так как MDE в данном случае совпадает с реальным эффектом, это значение всегда будет оставаться 50-м процентилем красного распределения.

В случае если значение мощности, которое мы подставляем в формулу, меньше 50%, вертикальная линия, соответствующая критическому значению будет лежать правее, чем MDE. Теперь изменение размера выборки будет влиять на мощность, что мы и видим выше на рисунке 2.

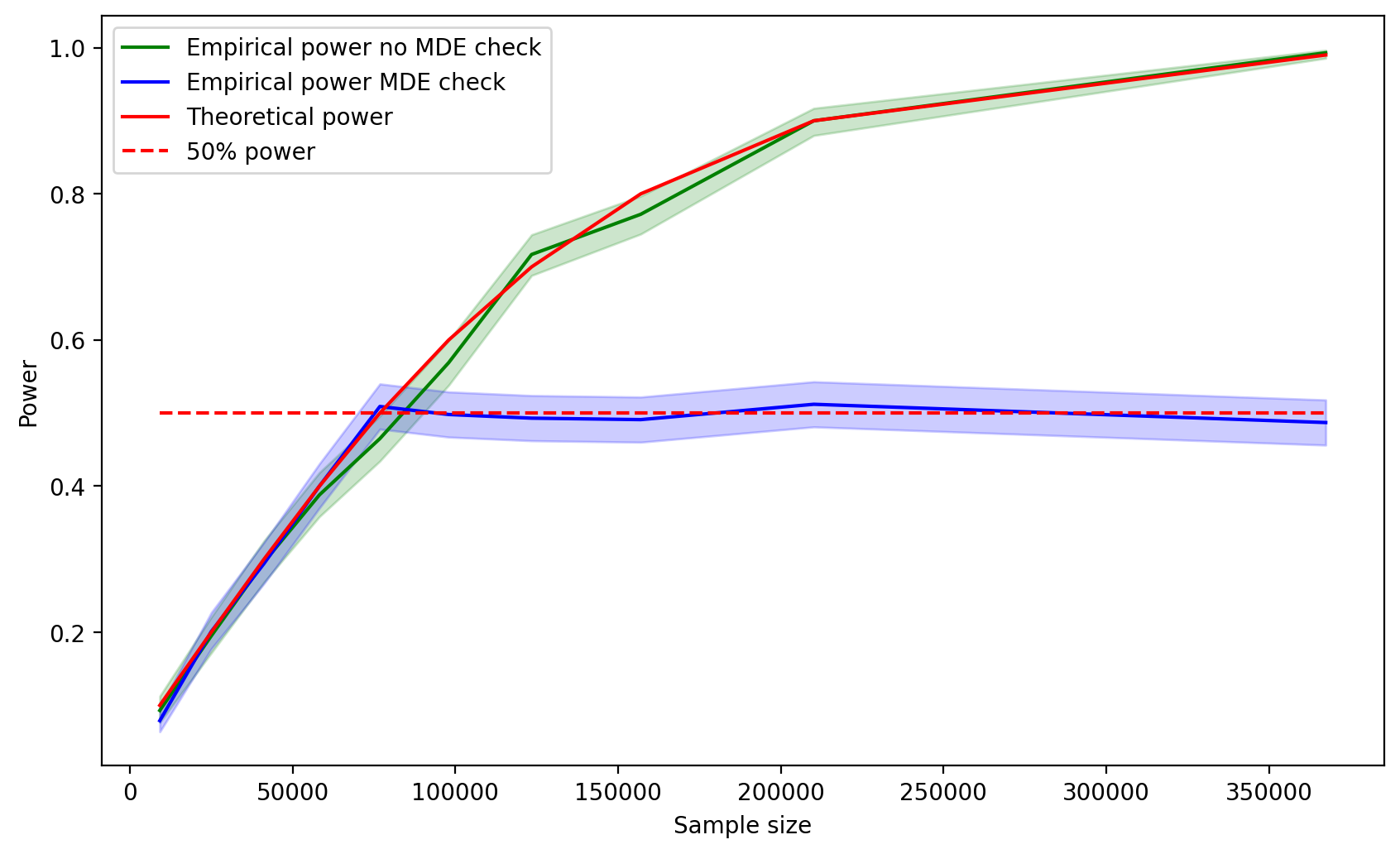
Для очистки совести проведем симуляции, убрав дополнительное условие на MDE в функции t-теста. Получаем хорошенького малыша:

Панч #3 (жесткий). Невозможность принять тест даже с бесконечной выборкой

В примере с симуляциями мы знали реальный эффект и подставляли его в формулу мощности. Но, как я говорил ранее, когда мы проводим настоящий эксперимент, никакого реального эффекта мы не знаем. И в такой ситуации использование MDE в качестве дополнительного критерия принятия теста может привести к такому большому приколу, что мама не горюй.

Давайте снова проведем симуляции. Зададим те же самые генеральные совокупности, но в качестве MDE возьмем не истинный эффект, который равен 3, а, например, эффект равный 5. Реальная ли это ситуация? Вполне. В условиях, когда мы не знаем истинного эффекта, мы можем взять в качестве предполагаемого как больший эффект, так и меньший.

Алгоритм действий будет очень похож на предыдущий, за исключением того, что теперь мы будем варьировать размер выборки и считать теоретическую мощность, а не наоборот.

# Зададим исходные параметры
mean_a = 1000 
mean_b = 1003
var_a = 90000
var_b = 90000
mde = 5 # Предполагаемый эффект!
sig = 0.025
z_sig = sps.norm.ppf(1-sig)
N = 1000
theoretical_power = []
real_power = []
left_real_power = []
right_real_power = []
sample_size = []

for n in tqdm_notebook(range(10000, 200001, 10000)):
    
    results = []
    z_power = z_sig-np.sqrt(n)*mde/np.sqrt(var_a+var_b)
    power = 1-sps.norm.cdf(z_power)
    
    for i in tqdm_notebook(range(N)):

        sample_a = sps.norm(loc=mean_a, scale=np.sqrt(var_a)).rvs(n)
        sample_b = sps.norm(loc=mean_b, scale=np.sqrt(var_b)).rvs(n)
        res = strange_ttest(sample_a, sample_b, z_sig, mde)
        results.append(res)  
        
    empirical_power = np.mean(results)
    # считаем доверительный интервал для вероятности успеха серии испытаний Бернулли
    left_real_level, right_real_level = proportion_confint(count=N*empirical_power, 
                                                           nobs=N, 
                                                           alpha=0.05, 
                                                           method='wilson')
    
    theoretical_power.append(power)    
    real_power.append(empirical_power)
    left_real_power.append(left_real_level)
    right_real_power.append(right_real_level)
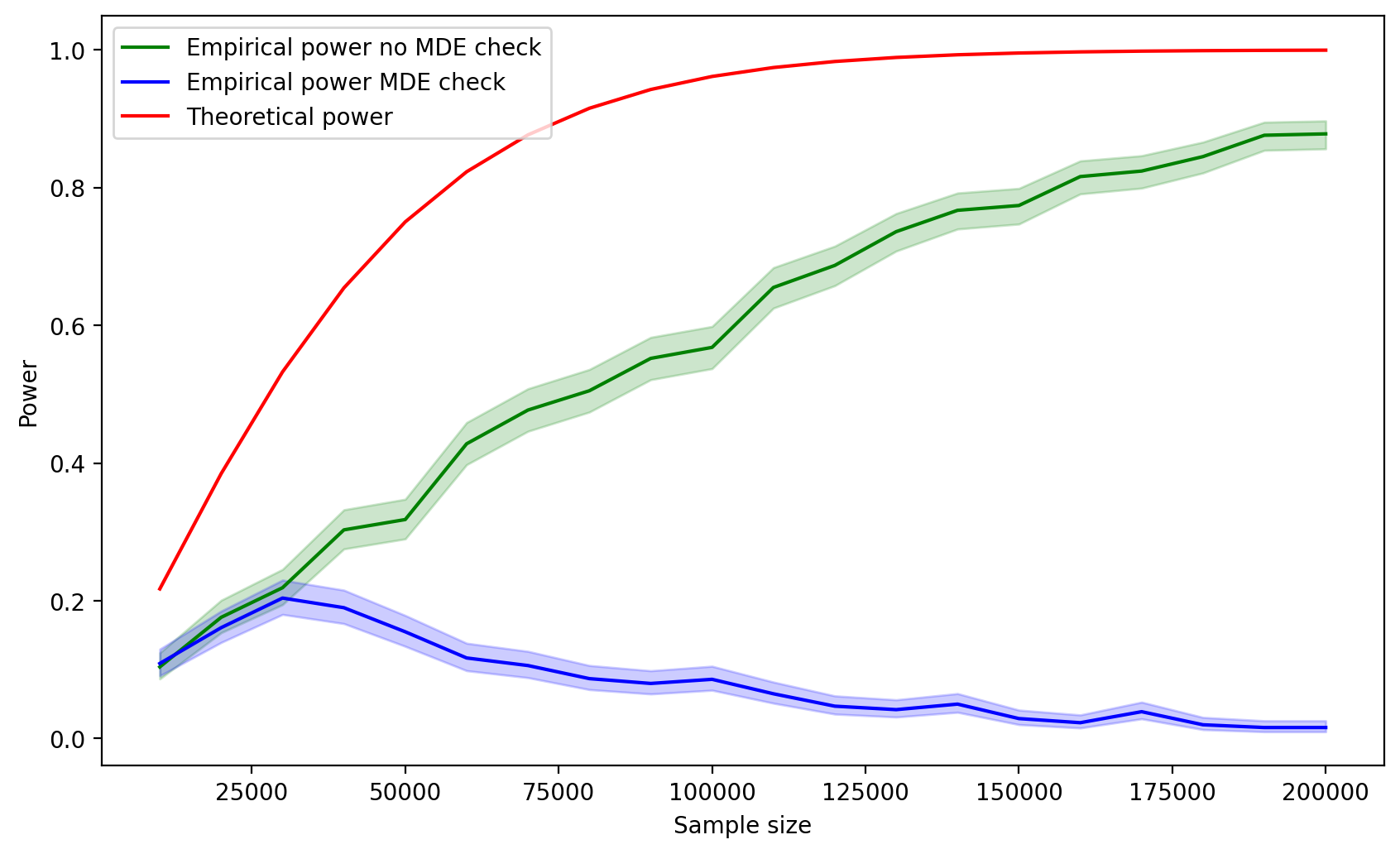
    sample_size.append(n)

А теперь давайте посмотрим на результаты:

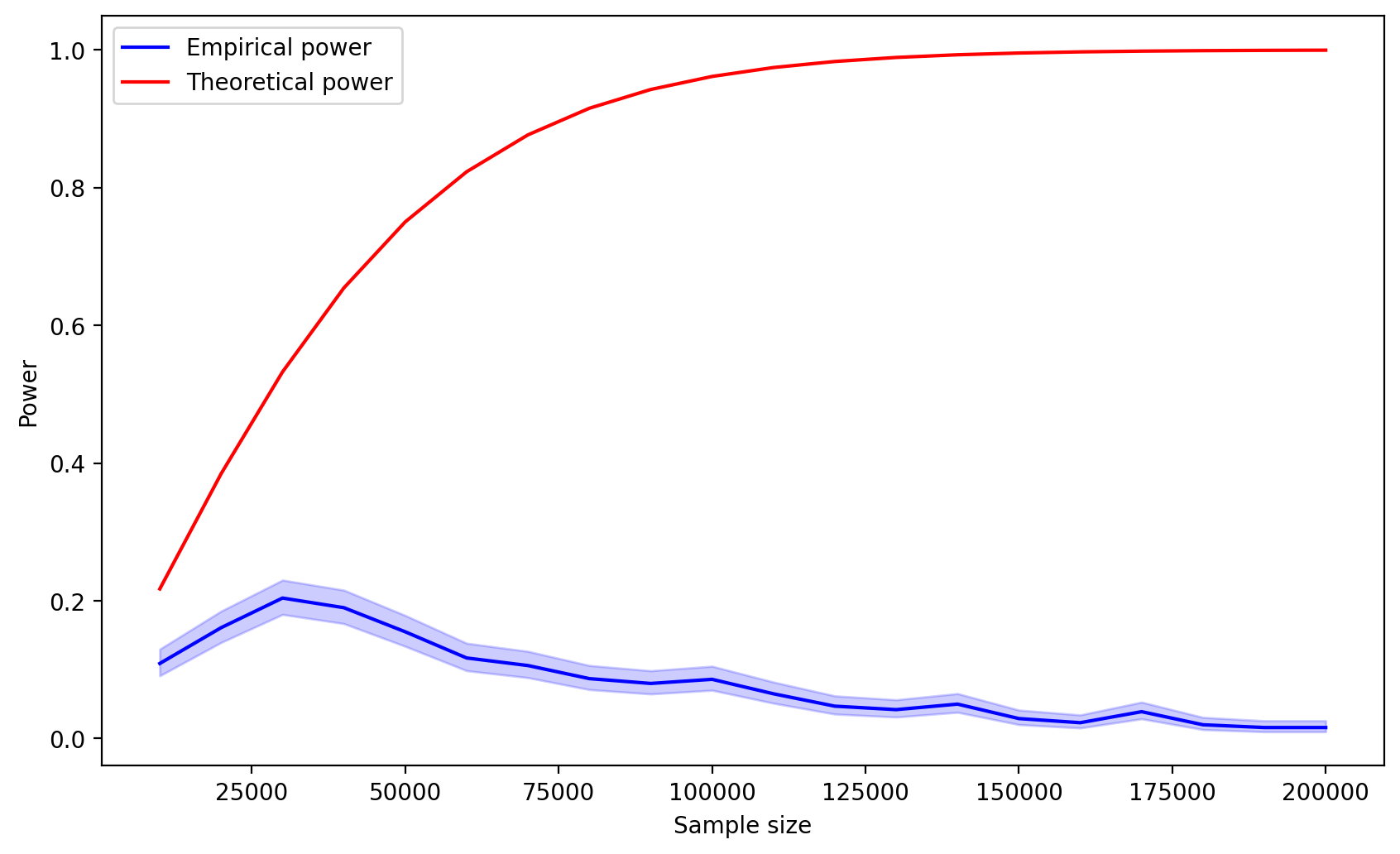
Почему-то с увеличением размера выборки мощность, полученная на симуляциях, уменьшается. Происходит это по следующей причине. Увеличение выборки уменьшает стандартную ошибку разности средних, что, в свою очередь, сужает распределение разности средних. Так как в качестве критерия принятия теста мы используем max(Critical value, MDE), а выбранный MDE лежит правее, чем реальный эффект, мы попадаем в ситуацию, когда при увеличении размера выборки, мы будем со все меньшей вероятностью получать такие значения разности средних, которые будут лежать правее фиксированного значения MDE.

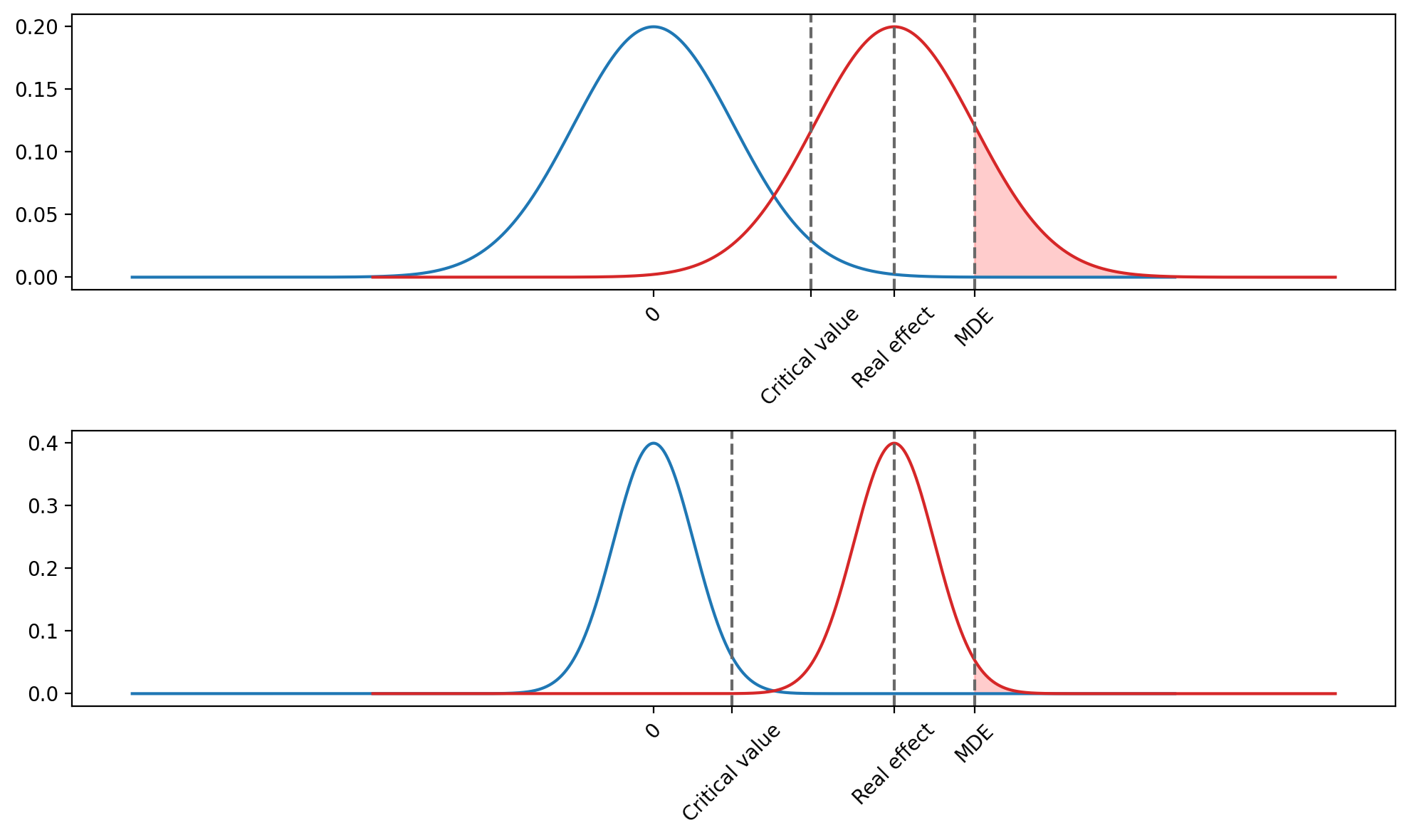
А теперь представьте ситуацию. Вы планируете A/B-тест и в качестве MDE выбираете эффект, который оказывается больше, чем истинный эффект от фичи. Но вы об этом не знаете. И тут вам в голову приходит мысль: «А дай-ка я на этот раз подержу тест подольше — чтобы мощность была не привычными 80%, а 99.9%!». И вот вы рассчитываете необходимый размер выборки, который равен примерно бесконечности, запускаете эксперимент и ждете. Выборка становится все больше, распределение разницы средних все у́же — уже такое тоненькое, что больно смотреть. А вы все ждете, и ждете, и ждете…

В конечном итоге вы получите распределение, 99.(9)% значений которого лежат на очень маленьком отрезке с центром в значении, равном истинному эффекту. Ваш предполагаемый эффект, в свою очередь, в этот отрезок не попадает и лежит правее. И вот, наконец, тест заканчивается. Вы получаете какую-то наблюдаемую разницу средних. Видите, что она лежит левее MDE и, будучи уверенными в том, что мощность у теста близка к 100%, обезумев от такого большого размера выборки, плюете на все правила статистики и принимаете нулевую гипотезу. Хотя на самом деле она неверна.

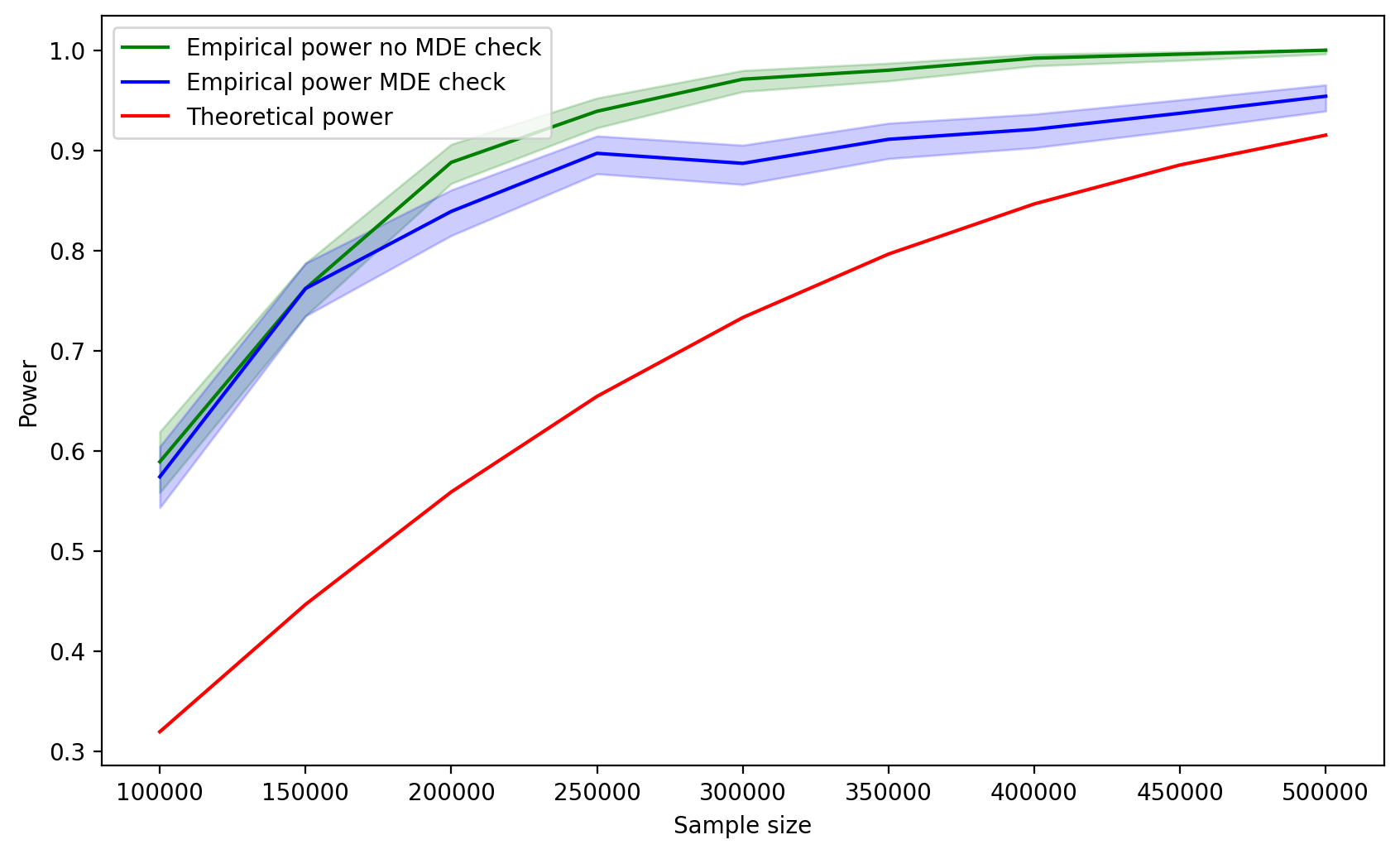
А что было бы, если бы мы запустили те же самые симуляции, но с функцией t-теста без сюрприза? Было бы вот что:

Ультимативный разбор мощности от Ромы Смирнова

Вот вы посмотрите на график на рис. 8 и скажете: «Ром, а тебе не кажется, что даже с твоим правильным t-тестом тут кое-что не в порядке? Да, эмпирическая мощность стала расти, но почему при этом теоретическая мощность стабильно принимает более высокие значения? Почему мы не получили хорошенького малыша, как на рисунке 5?».

Давайте подумаем, в чем отличие между этими двумя примерами? Отличие заключается в том, что в первом случае реальный эффект совпадал с предполагаемым, а во втором — предполагаемый был выше.

В первом случае при планировании эксперимента его параметры могли бы выглядеть так:

• Var = 90000

• alpha/2 = 0.025

• beta = 0.2

• power = 0.8

• Предполагаемый эффект = 3

• n = 156978

• Реальный эффект (мы его не знаем) = 3

Помните, я писал в статье, что мощность и MDE существуют только в рамках наших предположений о том, какой на самом деле эффект оказала фича? Давайте сделаем следующую вещь: подставим в формулу мощности все эти параметры, за исключением самой мощности и MDE. Для MDE вместо предполагаемого эффекта мы будем подставлять реальный. А мощность будем выражать из формулы. Сделав такую операцию, мы получим не предполагаемую мощность, а реальную. Другими словами, мощность, рассчитанную для MDE, равного истинному эффекту, при объеме выборки 156978.

Так как в данном случае реальный эффект и предполагаемый совпадают, реальная и предполагаемая мощности также будут совпадать. Более этого, это будет наблюдаться для любого значения n. Мы можем видеть это на рисунке 5. То, что я называл теоретической мощностью, соответствует предполагаемой мощности. Эмпирическая — реальной.

В втором случае при планировании эксперимента его параметры могли бы выглядеть так:

• Var = 90000

• alpha/2 = 0.025

• beta = 0.2

• power = 0.8

• Предполагаемый эффект = 5

• n = 56512

• Реальный эффект (мы его не знаем) = 3

Если мы сделаем ту же самую подстановку, то увидим, что реальная мощность для MDE = 3 и n = 56512 равна всего лишь 39%! Это происходит потому, что на этапе планирования эксперимента мы взяли слишком большой предполагаемый эффект и получили слишком маленькую выборку. Именно поэтому на рис. 8 мы наблюдаем, что для каждого значения n эмпирическая/реальная мощность меньше теоретической/предполагаемой.

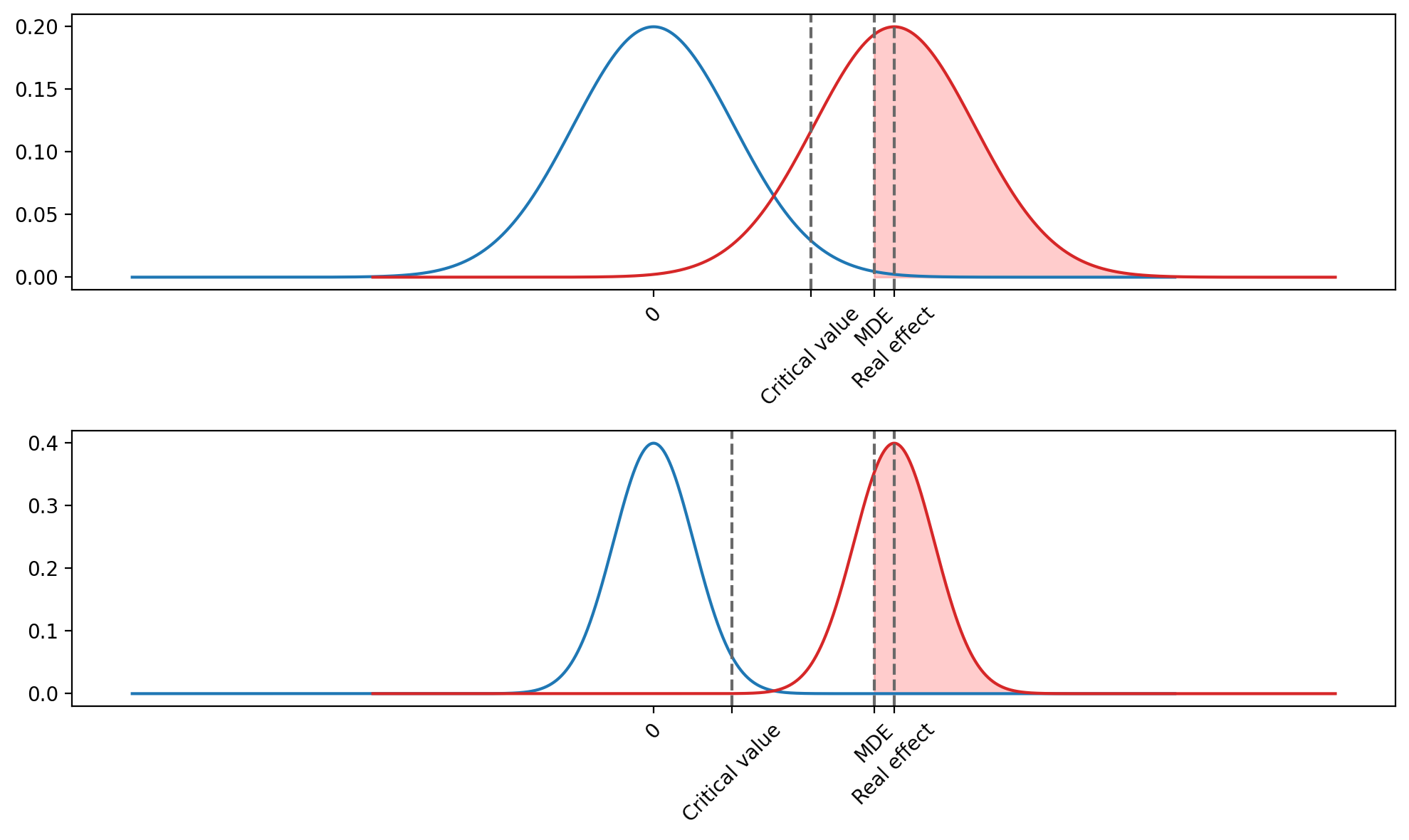
А теперь давайте проведем последние симуляции и посмотрим, что будет, если на этапе планирования эксперимента мы выберем MDE, который будет меньше истинного эффекта. Как и раньше, я сделаю это как для неверного способа принятия теста, когда наблюдаемый аплифт сравнивается и с критическим значением, и с MDE, так и для стандартного способа.

Для обоих способов принятия теста реальная мощность, что ожидаемо, оказалась выше предполагаемой. Действительно, подставляя в формулу мощности MDE меньший чем реальный эффект, мы получаем размер выборки, который превышает тот, что на самом деле необходим для достижения целевой мощности.

Как и в предыдущих случаях, до определенного момента две эмпирические мощности совпадают. После того, как критическое значение становится меньше, чем предполагаемый эффект, мощность стандартного t-теста начинает превышать мощность t-теста с сюрпризом.

При этом в отличие от случая, когда реальный и предполагаемый эффект равны, мощность t-теста с сюрпризом продолжает расти до конца, а не стабилизируется на какой-то отметке. Это происходит потому, что сейчас предполагаемый эффект не совпадает с реальным. Соответственно, MDE не лежит в центре распределения, соответствующего альтернативной гипотезе. А значит, изменение формы правого распределения влияет на итоговую эмпирическую мощность.

Так как же все-таки репортить мощность?

Никак. Вы можете сказать что-нибудь вроде: 

Для выборки данного размера мы обнаружим статистически значимое отклонение с вероятностью 80% при условии, что истинный эффект равен 3.

Для выборки данного размера мощность теста составляет 80% при условии, что истинный эффект равен 3.

Но это не означает, что мощность в действительности равна 80%, так как истинный эффект необязательно равен 3.

Да и вообще, как я уже говорил, в случае прокраса эксперимента забудьте о мощности и об MDE. Если наблюдаемый аплифт превысил критическое значение, сосредоточьтесь на нем и на доверительном интервале вокруг аплифта. Ширина доверительного интервала не зависит от наших предположений относительно MDE и мощности.

В случае, если тест не прокрасился, я бы также не стал использовать формулировку «если эффект и есть, то он точно ниже, чем тот, который мы подставляли в формулу в качестве MDE при планировании эксперимента».

Во-первых, давайте не забывать про то, что мы с вероятностью 20% могли не обнаружить эффект, даже если он в действительности равен предполагаемому.

Во-вторых, истинный эффект на самом деле может быть и больше, чем тот, что мы подставляли в формулу. Просто в таком случае вероятность не обнаружить его будет меньше 20%. Вот если бы мы провели 1000 A/B-тестов и увидели, что значение 0.8 лежит выше верхней границы доверительного интервала эмпирической мощности, то тогда, действительно, могли бы сказать, что реальный эффект меньше, чем предполагаемый.

Если хочется каким-то образом оценить размер реального эффекта на основе результатов серого теста, стоит обратить внимание на границы доверительного интервала. Если используемый статистический критерий верен, то при проведении эксперимента мы с вероятностью 95% получим доверительный интервал, в границах которого будет лежать реальный эффект.

Подведем итоги

• При планировании эксперимента следует различать понятия наблюдаемого аплифта, предполагаемого эффекта и реального эффекта.

• Сравнение наблюдаемого аплифта с предполагаемым эффектом для принятия теста — порочная практика. В лучшем случае это приведет к снижению мощности теста, в худшем — к непринятию фичи, которая на самом деле оказала эффект на метрику.

• Даже если вы используете стандартный подход для оценки результатов теста, нужно понимать, что та мощность, которую вы рассчитали при планировании эксперимента, является такой же предполагаемой, как и эффект, который вы подставляли в формулу мощности вместо MDE. Реальная мощность теста может оказаться как больше посчитанной, так и меньше.