Почему «уравнение Бернулли» не применимо в авиации и судостроении
Когда изучаешь предмет «Гидравлика» в ВУЗе, то там всегда рассматривают трубопровод с реальными размерами и твёрдыми стенками, по которому течёт вода от одного конца трубы до другого. Для этих реальных условий и было записано « Уравнение Бернулли» самим Бернулли ещё в 18 веке.
В исходном уравнении в правой части всегда присутствует дополнительный член- Lтрен, равный потерям на гидравлические сопротивления между двумя исследуемыми сечениями (вязкое трение самой жидкости, местные препятствия на стенках). (см.рис.1)

Рис.1. Фрагмент из учебника с описанием уравнения Бернулли для реальной жидкости.
Шли десятилетия и века. И вот в 20-м веке возникла мода на «теоретическую науку», где стали исследовать отвлечённые физические модели со свойствами, сильно отличающимися от реальных объектов и субстанция.
Так появилась «идеальная жидкость», в которой нет вязкого трения.
На основе этой идеальной жидкости (ИЖ) начали выстраивать объяснения к реальным явлениям, и тут ИЖ решили включить в «уравнение Бернулли» (УБ).

Рис.2. Фрагмент из учебника с описанием уравнения Бернулли для «идеальной» жидкости.
В результате такой вставки из правой части уравнения исчезла составляющая потерь Lтрен, что стало приводить к удивительным теоретическим результатам.(см.рис.2)
Так как ИЖ стала способна протекать по трубам разного профиля без потерь, то в теории начали возникать всевозможные «парадоксы». К таким неожиданным парадоксам относится и «Нулевое сопротивление движению шара сквозь ИЖ».
В чём причина появления «парадоксов по Бернулли»?
Основная причина противоречий ИЖ с реальностью состоит в том, что каким-то загадочным образом удаётся свободно трансформировать потенциальную энергию давления в кинетическую энергию и обратно без потерь и без применения дополнительных механизмов.
В реальной же жизни без потерь (почти или с КПД 99%) удаётся трансформировать давление в скоростной напор ускоренного потока жидкости в плавно сужающихся насадках.
В то же время обратный процесс (то есть торможение потока) самопроизвольно без потерь не протекает.
Торможение струи при расширении трубы протекает с появлением силы согласно закона Ньютона:
F=d(m*v)/dt= Q*q*(V1-V2)
Где Q- объёмный расход воды по трубе, q- плотность воды в трубе.
Для перевода силы F в давление добавочного напора dP необходимо силу разделить на площадь трубы в сечении S2
dP=F/S2
Так как поток в трубе имеет постоянный расход Q, то по условию неразрывности потока выполняется равенство
Q=V1*S1=V2*S2
Откуда получаем S2=Q/V2
И тогда dP= F/S2= Q*q*(V1-V2)/(Q/V2)
После сокращения Q в числителе и знаменателе получаем
dP = q*(V1-V2)*V2
Тогда для реальной маловязкой жидкости (воды) при расчётах для разных величин отношений V2/V1 в диапазоне от нуля (бесконечное расширение с полным торможением) до единицы (труба не расширяется вовсе) получается интересная закономерность возврата энергии из кинетической формы в потенциальный напор (см.рис.3-4 ).
По графику видно, что максимальный возврат напора достигает 50% при снижении скорости V2 в два раза (таб.серая строчка №6), что происходит при расширение сечения S2 потока в 2 раза (увеличение диаметра в 1,4 раза). При этом общие потери энергии в сечении S2 составляют 25% от кинетической энергии в сеченииS1.
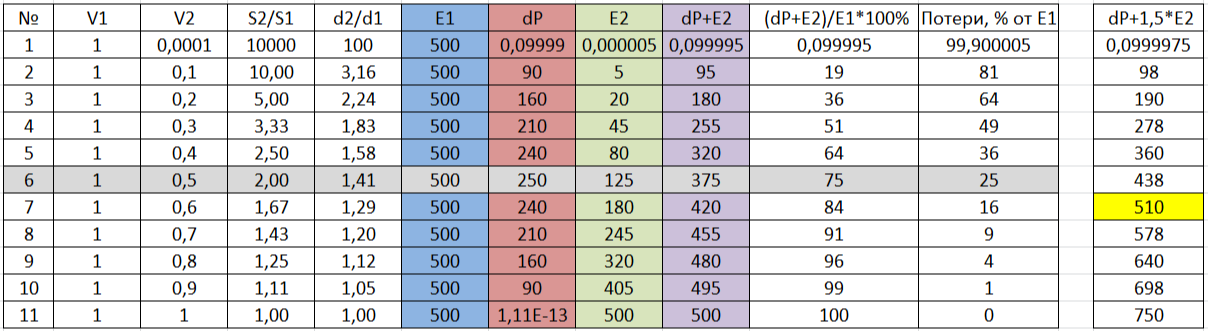
Рис.3 Расчётная таблица для графики изменения составляющих энергии между двумя сечениями S1 и S2 при различных соотношениях S1/S2.
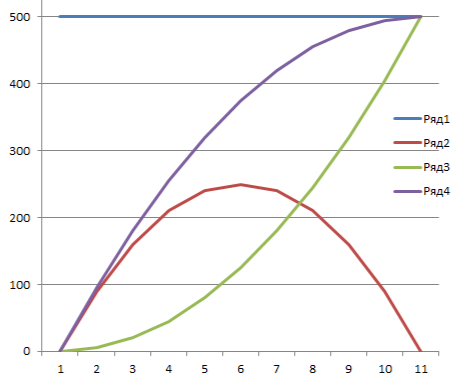
Рис. 4. Графики изменения составляющих энергии между двумя сечениями S1 и S2 при различных соотношениях S1/S2, то есть слева оси ОХ при х=1 значение S1/S2=0, что соответствует бесконечному расширению при V2=0, а справа при ОХ=11 предел расчёта при S1/S2=1, то есть совсем без расширения. Зелёная кривая- остаточная кинетическая энергия потока Е2 после расширения, красная кривая –прирост статического напора dР от торможения струи при расширении трубы, Фиолетовая кривая- сумма (Е2+dР), голубая горизонталь сверху- базовая кинетическая энергия Е1=500Па, что характерно для скорости потока воды в трубе V1=1м/c в сечении S1.
В остальных вариантах отношения V2/V1 прирост давления dP слева и справа от максимума оказывается меньше, чем при 2 кратном расширении потока.
В реальной жизни чтобы преобразовать скоростной напор (кинетическую энергию струи) обратно в статическое давление dP требуется применять некоторые специальные устройства.
К таким устройствам относятся различные турбины на ГЭС.
При этом на турбинах отводимая кинетическая энергия не возвращается в саму струю, а выводится из системы во вне к наружным потребителям и устройствам (электрогенераторы на ГЭС). А уже электроэнергия от ГЭС с помощью электродвигателей и насосов может поднимать и запасать напор в каких-то других водяных накопителях.
Второе противоречие «Уравнения Бернулли» (УБ)
Если же просто продлить логику УБ для ИЖ, то получится, что при расширении потока давление должно как-то само увеличиваться за счёт уменьшения кинетической энергии при падении скорости потока.
Так очень бы хотелось «теоретикам-идеалистам», но этого не происходит на практике ни с какой жидкостью.
Виновником непокорности ИЖ является «Закон сохранения импульса».
Так взаимодействие тел связано тремя законами Ньютона и законом сохранения импульса.
Именно закон сохранения импульса мешает возвратить всю энергию из кинетической в потенциальную при расширении трубы.
Чем больше расширение трубы, тем сильнее тормозится поток и тем больше потери энергии на тепловыделение при столкновении слоёв воды в их тормозном процессе.
Затормозить поток с высокой скорости возможно только при столкновении его с массой воды меньшей скорости, в результате получается общий поток равной скорости с сохранением общего импульса.
При таком торможении безвозвратно рассеивается часть кинетической энергии входящей струи, которая уходит сначала на образование вихрей в массе вода, а потом вся энергия из вихря уходит в тепло через вязкое трение.
Третье противоречие УБ для ИЖ
Идеальную невязкую жидкость невозможно затормозить!
Если же «теоретики» вспомнят, что ИЖ невязкая, то тут возникает другой парадокс, что идеальная труба с ИЖ вообще не может расширяться.
То есть идеальная струя ИЖ из-за своей идеальной скользкости не заметит расширения трубы, а будет проскальзывать сквозь покоящийся объём ИЖ в расширенной трубе так, будто продолжает течь по прямой трубе постоянного сечения.
Интересно, что для ИЖ практически нет картинок с расширением трубы!
Чаще всего рисуют одиночное сужение или цепочку последовательных сужений трубы (см.рис.5)
В тоже время для вязкой жидкости (с учётом потерь) картинки с расширением трубы можно легко найти. При этом на картинке обязательно представляют график монотонных потерь суммарной энергии потока от сечения к сечению по ходу потока (см.рис.6).
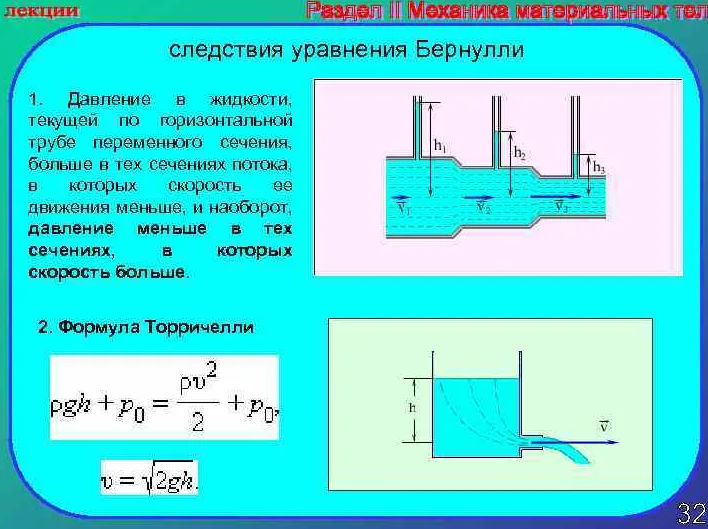
Рис.5. Рисунок из учебника с уравнением Бернулли для «идеальной жидкости», где потерь от сечения к сечению нет. Правда на картинках показаны только сужения трубы с разгоном струи, где и для вязкой воды трансформация энергии составляет 99%.
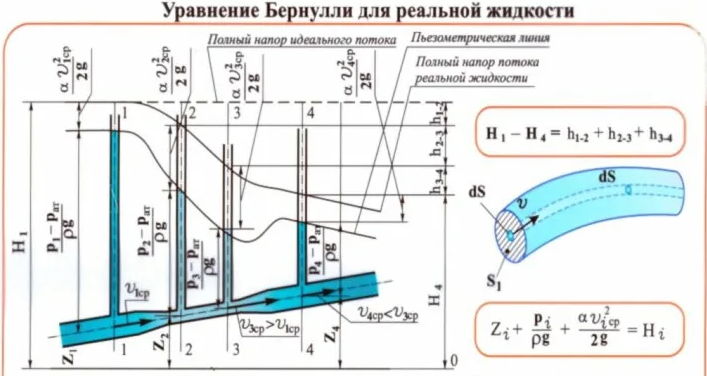
Рис.6. Рисунок из учебника, где выделены независимо два графика: Пьезометрическая линия- идёт с подъёмами и спусками при изменении диаметров трубы и скоростей потока, Полный напор- постоянно монотонно убывает по длине (за счёт вязких потерь). Сверху пунктиром постоянная энергия для «Идеальной жидкости».
Четвёртое противоречие УБ
Четвёртым противоречием УБ и его применения вне замкнутой твёрдой трубы является то, что в УБ никак не рассматривается динамика потока на изгибах стенок трубы (при поворотах или изменении сечения).
Центростремительное давление- это побудительная сила для изгибания струи.
Центростремительное давление на резком повороте трубы просто обязано возникнуть, чтобы обеспечить выполнение закона Ньютона при круговом движении с центростремительным ускорением. Ведь в жидкости есть отдельный массивные молекулы, которые по отдельности так же обязаны подчинятся законам Ньютона наравне с крупными телами.
Так как центростремительное давление на слой жидкости действует строго поперёк вектора скорости, то никакой полезной работы вдоль потока оно совершить не может. Это как неподвижный гвоздь в стене, который годами держит на себе тяжёлые полки, но при этом никакую энергию не расходует.
Интересно рассмотреть характер изменение давления по сечению потока и на стенках при поворотах трубы.
Для этого «теоретики» начинают рисовать распределение скоростей потока на повороте, напрямую однозначно связывая поперечные давления со скоростями потока через УБ.(см.рис.7)
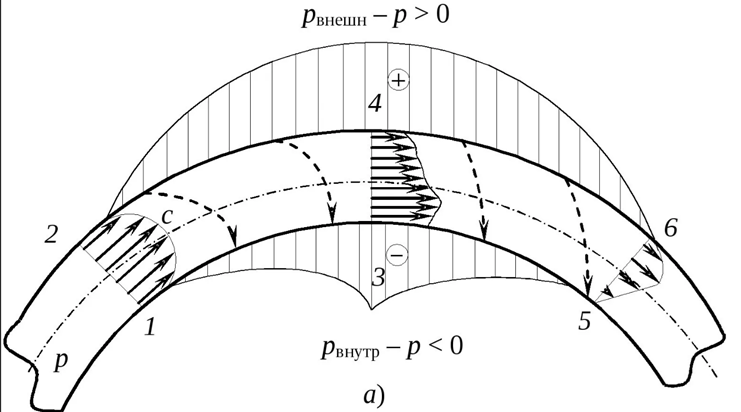
Рис.7 Картинка из учебника, где авторы сделали попытку подогнать экспериментальные данные по давлению на стенки в повороте трубы под теоретическую модель с УБ.
По факту же поперечное давление на стенке трубы – это сумма центростремительных давлений элементарных слоёв жидкости по сечению трубы, а потому замеряемое манометром давление на стенке никак не может определить характер распределения скоростей в трубе.
В тоже время одинаковое дополнительное центростремительное избыточное давление на внешней стенке поворота трубы будет создаваться как при сложном распределении скоростей по сечению, так и при постоянной скорости потока по сечению струи.
Та же ситуация неодинаковости давлений по направлениям наблюдается в обычном неподвижном стакане неподвижной воды, где давление по вертикали меняется, а по горизонтали в каждом уровне оно постоянно. Если же этот стакан поместить в аттракцион «Центрифуга» (см.рис.8), то поверхность воды в стакане станет вогнутой (параболоид вращения), и такой же вогнутой формы будут изобарические слои на всю глубину жидкости в стакане. (см.рис.9)
На основе такого формообразования жидкости во вращающейся чаше делали оптические зеркала телескопов, используя в качестве жидкости легкоплавкие металлы (ртуть или легкоплавкий сплав галлия). Такие зеркала имели практически идеальную геометрическую форму и были достаточно дёшевы, но могли при этом смотреть только вертикально в верх (зенитный телескоп), что для телескопа не очень удобно.

Рис.8. Аттракцион «Центрифуга», где вектор локальной «гравитации» направлен от оси вращения центрифуги к его периферийным стенкам. Таким образом, свободная поверхность воды в сосуде на этой центрифуге будет иметь вогнутую кривизну ( фрагмент параболоида вращения).
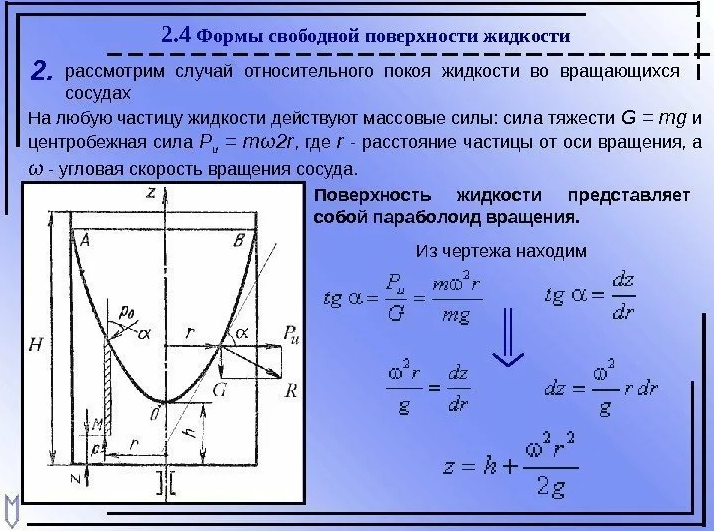
Рис. 9. Теоретическое обоснование формы поверхности жидкости во вращающемся сосуде.
На картинке потоков в повороте (см.рис.7 ) пунктиром показаны ещё и дополнительные закручивания потока в загнутой трубе. И это завихрение потока в спиральный жгут действительно имеет место на практике!
В реальных трубопроводных системах после выхода потока воды из поворота даже специально требуют устройства прямых участков труб длинной не менее L=10*D, чтобы вращение потока воды успело затормозится о стенки прежде, чем поток попадёт на регулирующую арматуру или на водосчётчики.
Принятие идеи закручивание потока в повороте трубы даёт сразу вполне адекватную механическую картину как прохождения отдельных элементарных струек в общем пучке, так и позволяет рассчитать параметры водяного жгута из отдельных струек с учётом известных (экспериментальных) гидравлических потерь на повороте конкретной трубы.
Так известно из справочников, что в водопроводе сопротивление отдельного поворота стальной трубы диаметром 1 дюйм на 90 градусов составляет приблизительно
dЕ=0,5*Ек2
Для более общих случаев и некоторого наукообразия в учебниках дают эмпирические зависимости, то есть дающие похожий результат к экспериментально полученным графикам. (см.рис.10)
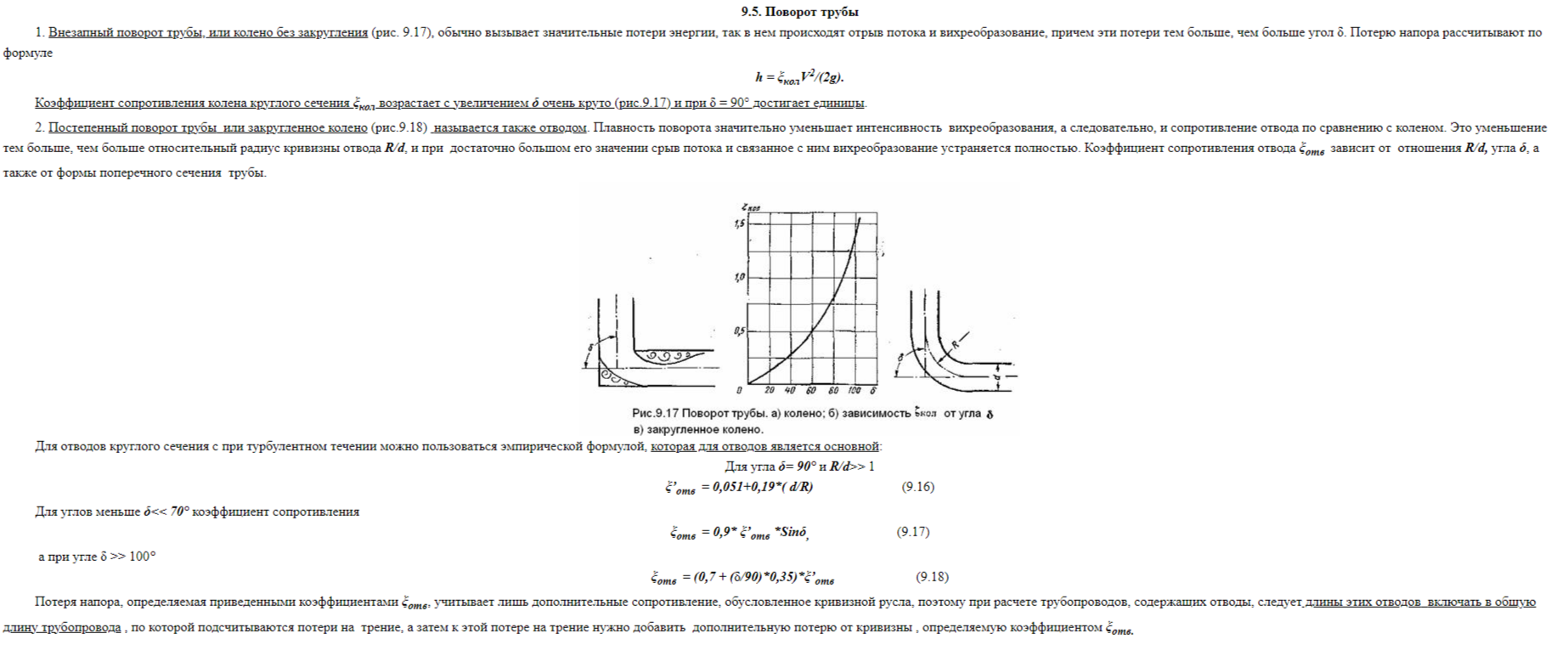
Рис.10. Фрагмент главы учебника «Гидравлика» про местные сопротивления на поворотах труб. В тексте учебника упоминается, что зависимости для сопротивления поворота являются эмпирическими.
Также в тексте упоминаются вихри в повороте трубы, но не уточняют где и в каком направлении закручены эти вихри. При этом в пояснительном рисунке (слева) показан ломаный поворот с резким сочленением стенок под прямым углом, где явно указаны зоны отрыва потока от стенок трубы с формированием застойно-вихревых зон между отрывными потоками и стенками труб.
В этих заторможенных зонах наблюдаются разные переменные по сечению поперечные давления: избыточные давления с внешней стороны поворота (до уровня скоростного напора в данном сечении), и разрежение во внутренней стороне поворота ( вплоть до вскипания воды при давления насыщенных паров при данной температуре, то есть до появления так называемого явления «Кавитация»). Но в тексте учебника про характер давления в этих застойных зонах с разных сторон поворота вообще не упоминается.
Зная справочное местное сопротивление dЕ=0,5*Ек2 для стандартного поворота на 90 градусов (круто загнутый отвод, где R/d=1), можем рассчитать геометрические параметры закрученного жгута элементарных струек потока в таком отводе.
При учёте одинакового диаметра трубы до и после поворота получаем, что в повороте возникло плавное заужение отдельных струек, а, следовательно, и разгон потока в них до более высокой скорости с КПД близким 100%.
В дальнейшем, на выходе из поворота трубы, поток затормозится обратно в расширенный исходный диаметр трубы. При этом вращение потока остановится вязким трением и локальным вихреобразованием о шероховатость стенок, выделив лишнюю энергию от вихреобразования в виде тепла.
Из известной величины потерь dЕ=0,5*Е2 и проведённых ранее расчётов можно записать уравнение:
Е1-(dP+E2)= 0,5*Е2
Откуда получим:
Е1= 0,5*Е2+(dP+E2)= dP+1,5*Е2
Из таблицы легко определить, что такое равенство достигаются при торможении потока приблизительно до V2=0,6*V1. (см. жёлтую клетку в правом столбике таб. рис.3)
Из чего можно сделать вывод об угле закручивания потока CosА=0,6, что даёт угол потока А=53 градуса к оси трубы. (см.рис.11)
То есть получается достаточно крутая спираль, которая на картинке учебника показана достаточно правдоподобной по углу наклона к оси трубы.
В пересчёте на шаг винта этот угол А=53 градуса приблизительно соответствует двум диаметрам длины трубы на один оборот спирали. (см.рис.11)
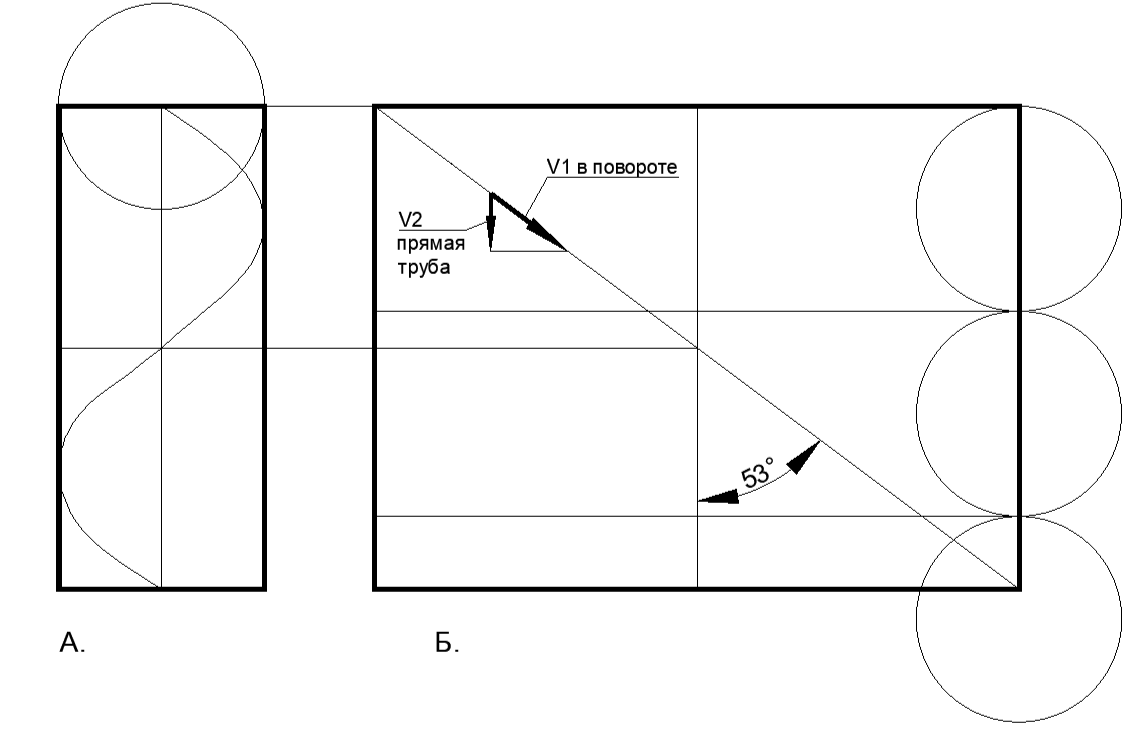
Рис. 11. Прямая труба с винтовой линией под углом 53 градуса. А- цилиндр с винтовой линией. Б-развёртка цилиндра с винтовой линией.
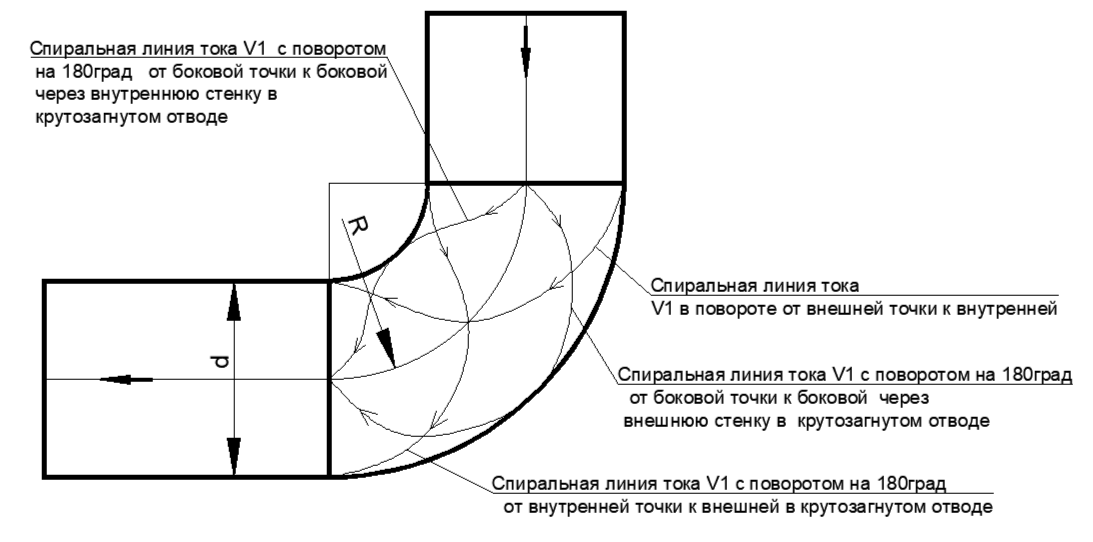
Рис. 12. Предполагаемый вид винтовых линий под углом 53 градуса с поворотом на 180 градусов в круто загнутом отводе, где R/d=1. Показаны четыре линии вдоль внутренней поверхности отвода с шагом в 90 градусов друг от друга.
В случае выстраивания спирали в круто загнутом отводе получается, что линии тока имеют разную длину, и при одинаковой скорости на входе в спираль достигают выхода не одновременно, а со сдвигом по сечению. Самые длинные пути идут по внешнему обводу от середины сечения к середине сечения, самые короткие пути - через внутренний обвод от середины к середине сечения.(см.рис.12)
В крупных воздуховодах, где нежелательно вихреобразование (например, в больших аэродинамических трубах) используют повороты с сепараторами потока, где на решётке с узкими поворотными лопатками резко поворачивают тонкие слои воздуха сразу на нужный угол (см рис.13-15)
Сопротивление таких поворотов с сепараторами очень мало, и достигает величин 0,05 (или 5% потерь от скоростного напора), вместо 50% в круто загнутых отводах без сепаратора.
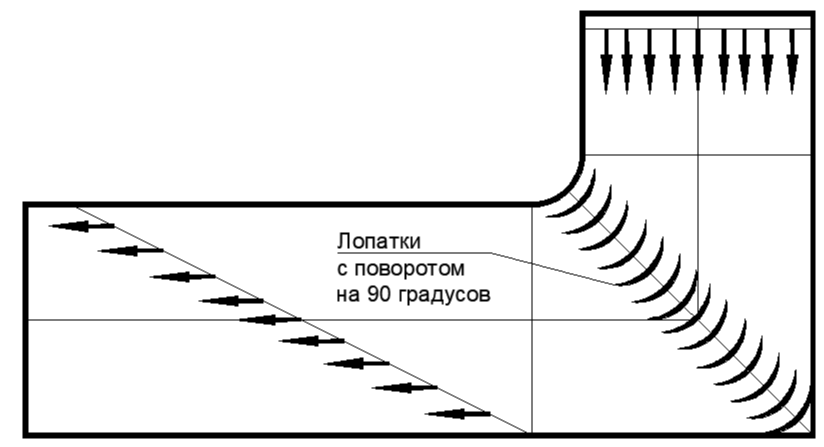
Рис. 13. Узел сепаратора потока в безвихревом поворотном колене на 90 градусов. Путь потока по слоям так же не одинаков: внутренний слой опережает наружный слой на два габарита колена.
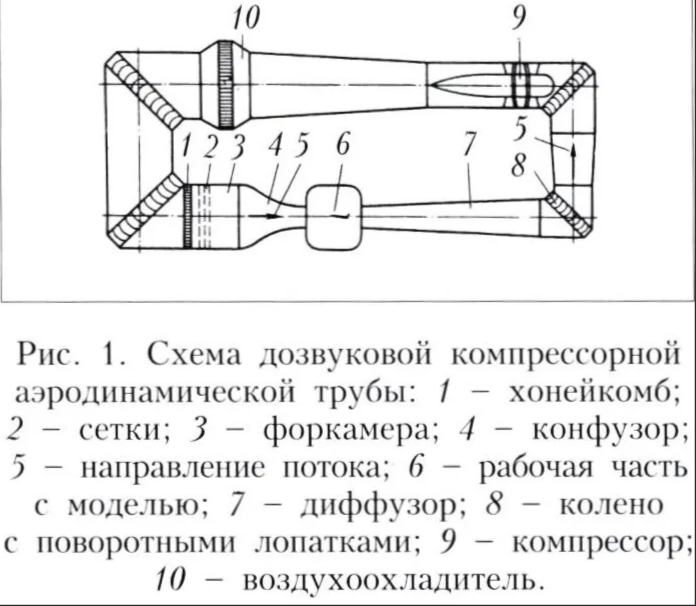
Рис.14. Рисунок из учебника со схемой АДТ, где поворотное колено воздуховодного тракта с поворотно-направляющими лопатками указано отдельным пунктом 8.

Рис. 15. Узел сепаратора потока в безвихревом поворотном колене на 90 градусов внутри гигантской аэродинамической трубы в ЦАГИ.
Экспериментальное подтверждение течения жидкости в повороте
Крайне интересно то, что можно поставить простой опыт и доказать несостоятельность распределения давления и скоростей по УБ.
В случае крутого изгиба трубы давление на внешней стороне трубы достигает величины скоростного напора в сечении, что по УБ потребовало бы полной остановки потока у внешней стенки поворота. Вот только на практике такой полной остановки потока на внешнем радиусе колена не наблюдается.
Проверяется это на простом экспериментальном устройстве, а именно: на коротком куске мягкого прозрачного шланга, где иголкой прожигается два отверстия в одном сечении с противоположных сторон одного диаметра.
Если обеспечить из шланга расход воды, то из двух боковых отверстий прямого шланга потекут тонкие струйки воды одинаковой интенсивности. Эти струйки возникают от давления потерь напора по длине шланга до излива в атмосферу, а также от гидростатического давления на половине диаметра шланга над отверстиями.
Если шланг начать изгибать в горизонтальной плоскости в зоне дырочек, то струи начнут меняться: из внешнего отверстия струя ускорится и станет бить дальше, а из внутренней поверхности струя уменьшится, и в какой-то момент при увеличении загиба остановится вовсе.
Для демонстрации отсутствия торможения до нуля у внешней стенки достаточно в отверстие впрыснуть красящее вещество и проследить его движение по прозрачной трубке.
Если продолжить сгибать шланг до небольшого залома в сечении, то внутренне отверстие начнёт подсасывать воздух, что будет видно по появлении цепочки пузырьков от отверстия в струе воды.
То есть на внутренней стенке поворота трубы давление упало до внешнего атмосферного давления, или даже ниже (при всасывании пузырьков воздуха внутрь потока).
Если установку чуть усложнить, вставив тонкие трубочки в отверстия и подняв их вертикально вверх, то по уровню воды в этих пьезометрических трубках можно будет судить о статическом напоре в зоне отверстий экспериментального шланга. (см.рис.16)
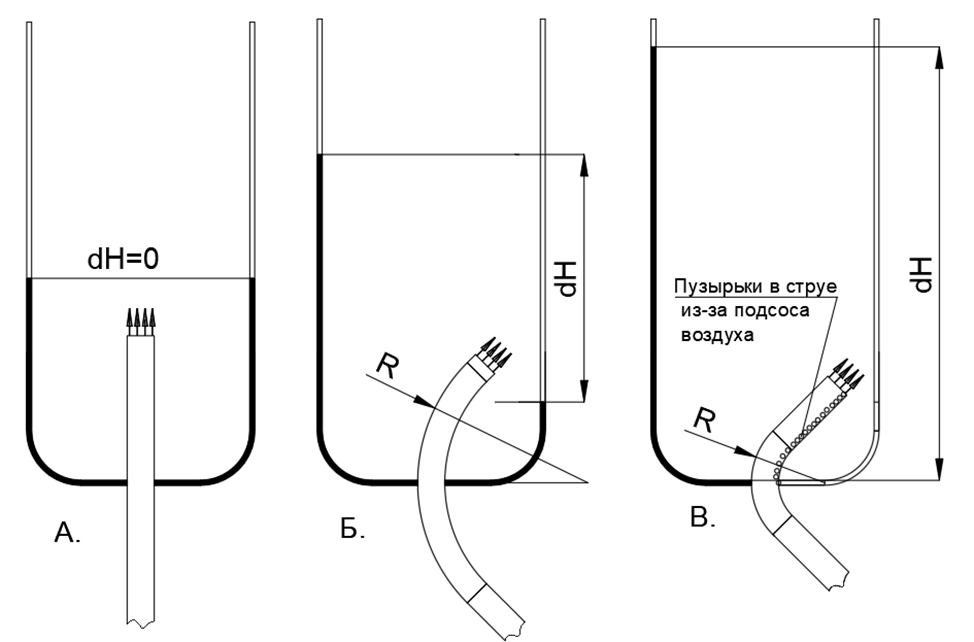
Рис. 16. Эксперимент по замеру бокового давления на стенку трубы в повороте: А- на прямой трубе нет перепада давления между противоположными стенками одного сечения, высота пьезометра в тонких трубках соответствует сопротивлению малого участка трубы до излива в атмосферу; Б- труба загнута с большим радиусом кривизны R, что создало перепад давления dH между стенками снаружи и внутри поворота; В- крутой загиб трубы с малым радиусом кривизны R (возможен залом трубы), так что давление на внутренней стенке в повороте упало ниже атмосферного, из-за чего начался подсос воздуха внутрь трубы.
Практические приложения эффекта центростремительного давления воды на искривлённые стенки
Существуют примеры технических устройств, где скорость потока по изогнутой стенке постоянна по сечению, и при этом давление на внешнюю стенку оказывается очень большим, а на внутренней стенке избыточное давление вообще отсутствует (т.е. равно атмосферному).
Простейший пример такого изгибаемого потока – это обычная обеденная ложка под струёй воды в кухонной мойке (см.рис.17 ). При этом на ложке ощущается весьма большая сила, изменяющаяся при изменении наклона ложки к струе из крана. Чем острее угол к струе- тем меньше сила от струи на ложке.

Рис.17 Разворот компактной цилиндрической струи из крана в плоский поток на вогнутой поверхности ложки (ковша).
Существуют и куда более масштабные устройства похожего типа, но уже для промышленного применения.
Так в открытой турбине Пельтона (ковшовая турбина) струя огибает полукруглый ковш турбины, при этом давя на него. При таком огибании ковша с вогнутой стороны потока (внутрь поворота) давление воздуха равно атмосферному и одной стенки у ковша нет вовсе (см.рис.18-19).
На выходе из ковша турбины струя имеет противоположное направление относительно направления исходной струи, при этом сохраняется постоянной скорость потока относительно самого ковша во время огибания тонким слоем воды вогнутой поверхности ковша. (см.рис.20-21)
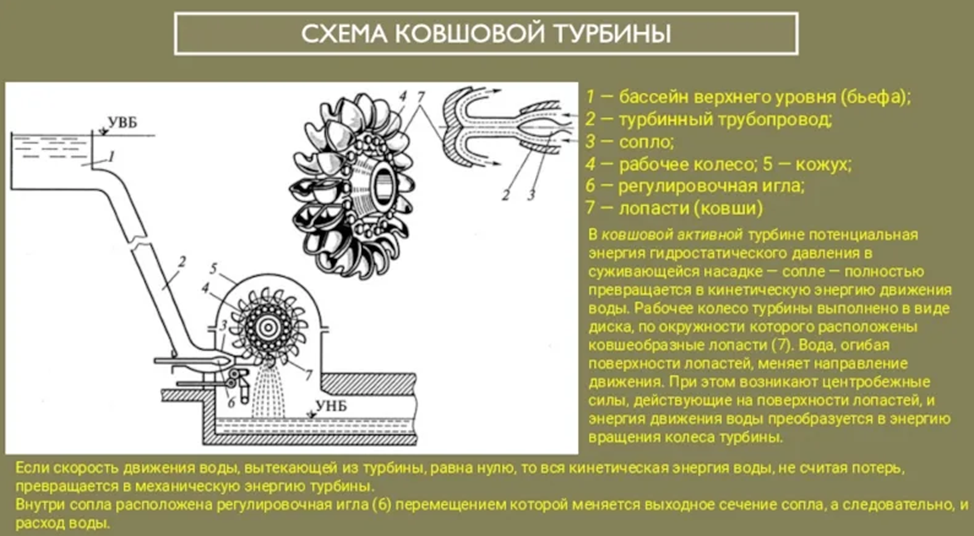
Рис. 18. Картинка с описанием работы турбины Пельтона (ковшовой турбины).

Рис. 19. Разрез корпуса турбины Пельтона (ковшовой турбины).
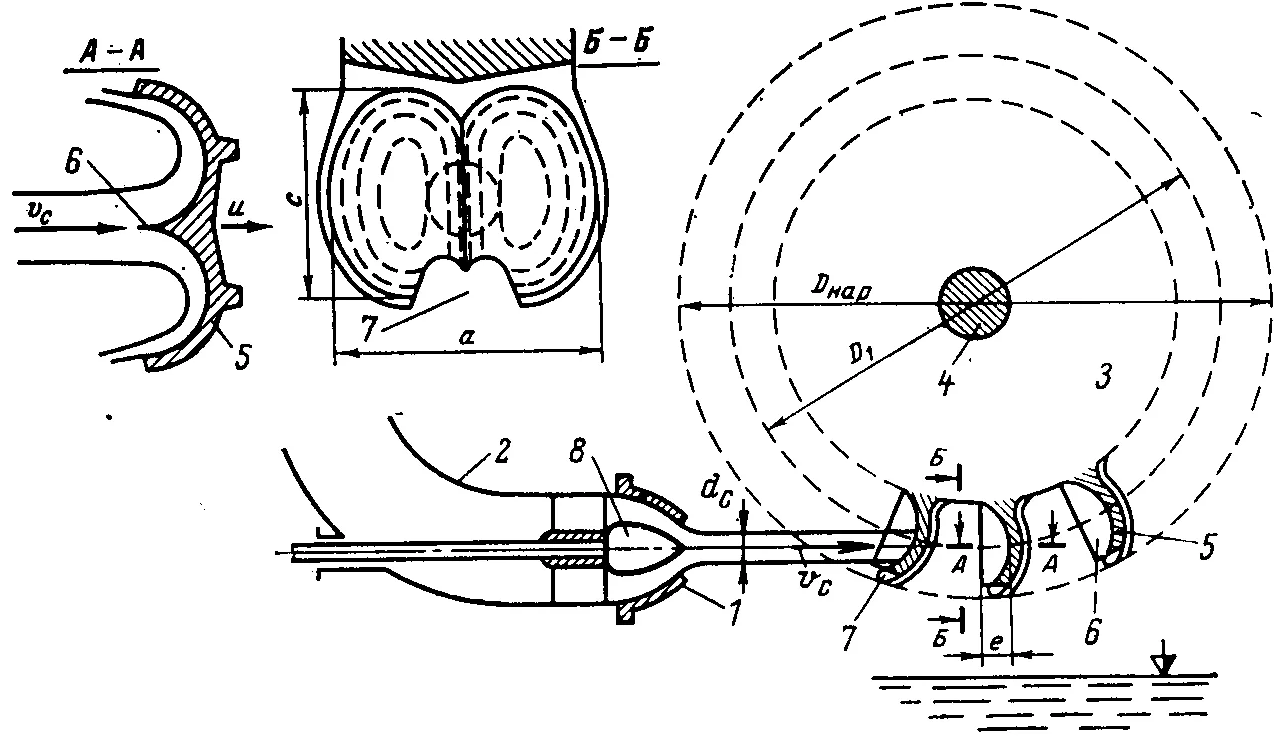
Рис. 20. Схема распределение потока воды из сопла по ковшу турбины Пельтона (ковшовой турбины). Цилиндрическая струя рассекается пополам центральным гребнем на две половинки ковша, после чего потоки растекаются веером с утонением слоя воды к выходу из ковша.
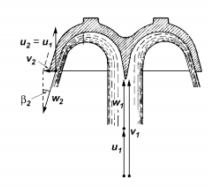
Рис. 21. Работа струи на ковше турбины Пельтона. В разрезе струи виден поворот тонкого слоя воды на 165-170 градусов в полукруглом ковше. Поворот до 165 градусов (не до 180 град) необходим для свободного сход потока мимо следующего ковша. Недоворот в 15 градусов снижает КПД на величину: ((sin15)/2)^2=0,017 или на 1,7%.

Рис. 22. Турбина Пельтона со снятой крышкой кожуха. Внутри кожуха давление равно атмосферному, а сам кожух нужен для защиты окружения от брыз с турбины и удержания турбины на фундаменте. Видно, что данная турбина крепится консольно непосредственно на толстом валу электрогенератора, а в кожухе вовсе нет опорных подшипников. При этом уплотнение вала в кожухе имеет вид лёгкой брызгозащиты, не способной выдержать никакого избыточного давления.

Рис. 23. Турбина Пельтона в кожухе. Видно, что у данной турбины в корпусе имеются независимые подшипниковые опоры, а на выходном валу установлен большой маховик, сглаживающий пульсации турбины при переходе струи с ковша на ковш. Труба малого диаметра с ручным вентилем от основного водовода – это подача струи для торможения турбины при отключении основной струи.
Наибольший КПД турбины Пельтона достигается тогда, когда скорость ковша в два раза меньше скорости воды из сопла. Этот режим называется номинальным режимом работы турбины, а общий КПД ковшовой турбины с вязкой холодной водой достигает более 90%.
То есть полное торможение воды на выходе из ковша достигается если окружная скорость ковша составляет половину скорости струи из сопла.
Vcт=2*Vковш
Vст-вых=- Vковш
Затормозить воду на турбине полностью нельзя, так как нужно обеспечить её отвод от турбины вбок. Для этого используют небольшой недоворот потока на 10-15 градусов на выходе из ковша.
Если сложить скорость ковша на номинальной скорости вращения турбины и скорость потока воды относительно земли, то скорость струи на выходе из черпака турбины будет иметь только небольшую тангенциальную составляющую вдоль оси турбины, при этом радиальная скорость потока будет равна нулю.
Так скорость отхода воды вбок от плоскости колеса турбины при угле кромки ковша 15 градусов к плоскости турбины составит:
(sin15)/2=0,13 или 13% от скорости V1 струи на сопле турбины.
При этом уносимая потоком энергия квадратична скорости потока и составит величину:
0,13^2=0,0167 или 1,7% первоначальной энергии струи.
Применение турбин Пельтона
Турбины Пельтона используют в ситуациях, когда напор воды на ГЭС велик, а расход воды сравнительно мал.
Такое случается на высокогорных ГЭС малой мощности, где небольшой сток ручья из горного озера (водохранилища) отводят по напорной трубе к турбине ГЭС где-то внизу в долине.
При этом перепад высот для ковшовых турбин Пельтона достигает нескольких сотен и даже тысяч метров, чего не бывает даже на гигантских ГЭС (невозможно построить плотину высотой даже 500м, а самые высокие реально созданные плотины имеют высоту около 300м).
Но на высокогорных ГЭС с турбинами Пельтона высоких плотин не строят вовсе, ограничиваясь длинной трубой от высокогорных озёр. В самой же трубе поток воды течёт на низкой скорости, тем самым уменьшая потери напора на трение о стенки напорного водовода ГЭС.
В австрийском городке Майрхофен (горнолыжный курорт а Альпах) такая ГЭС с турбиной Пельтона стоит прямо в центре городка, сбрасывая отработанную воду в ручей. Этот ручей берёт начало высоко в горах из небольшого запруженного водохранилища, от которого по толстой трубе и питается сама ГЭС.(см.рис.24)

Рис.24. Деривационная ГЭС в центре курортного города Майрхофен (Австрия). Мощность 345МВт. Перепад высот от питающего аккумулирующего пруда 480м, горизонтальное расстояние до аккумулирующего пруда 5км.
Пруд для ГЭС Майрхофена подпитывается сбросом от двух больших более высокогорных водохранилищ с собственными обратимыми ГЭС, образуя единый каскад с компенсирующим прудом-гидроаккумулятором над Майрхофеном.
Интересно, что весь объём своего пруда Майрхофенская ГЭС сработает всего за 20 часов работы на полной мощности. То есть Майрхофенская ГЭС вторична по отношению к сбросу воды при работе ГЭС от выше лежащих более крупных водохранилищ.
Из-за малости суммарного объёма всех водохранилищ данного гидроузла получается, что основная функция этих ГЭС- это работа в пиковом режиме, для компенсации коротких всплесков нагрузки суточного графика потребления энергосистемой Австрии.
Второй важной функцией гидроаккумулирующих реверсивных ГЭС является подстраховка более инерционных тепловых электростанций (ТЭС), когда при резком падении спроса на электричество избыточный поток электроэнергии от ТЭС нужно куда-то сбрасывать: например срабатывать лишнее электричество от ТЭС на обратную закачку из пруда-аккумулятора обратно в водохранилища при насосной работе обратимых ГЭС.
ГЭС- это практически самый быстрый по маневренным возможностям источник электроэнергии, также быстро обратимая ГЭС способна стать стольже мощным потребителем электроэнергии.
Сзади здания ГЭС (на фото справ вверху) видны выходящие из горы две толстых трубы- водовода диаметром более 2 м (в сравнении с легковушкой рядом). Мощность 345 МВт с общим КПД ГЭС около 80% при давлении 4,8МПа (480м.вд.ст=48атм) достигается при расходе 345/(0,8*4,8)=90м3/с
Скорость струи на турбине составляет Vс=0,99*(2*9,81*480)^0,5=96м/с
Окружная скорость ковша турбины Vт=Vc/2=48м/с
Диаметр турбины подбирают так, чтобы частота вращения колеса была кратна частоте тока 50 Гц.
Так при диаметре турбины около 2,5м частота вращения составит 5 об/с, что потребует использовать 10 полюсный электрогенератор для получения стандартной частоты 50Гц.
Если считать скорость в трубе водовода около 8м/с (как на плотинных ГЭС), то расход 90м3/с потребует сечения одного водовода
S= 90/(8*2)=5,6м.кв
или диаметр каждой трубы по D=2,7м.
D=(5,6/3,14)^0,5*2=2,7м.
Рядом с ГЭС на постаменте стоит старое рабочее колесо, отслужившее свой срок на ГЭС, типа как на фото (см.рис.25 ). Турбину вмуровали в бетон постамента видимо для того, чтобы её случайно не сдали в металлолом ушлые европейцы.

Рис. 25. Отработавшая свой ресурс турбина Пельтона на постаменте рядом с ГЭС.
Для закачки воды из аккумулирующего пруда обратно в большие водохранилища на двух соседних ГЭС используют обратимые турбины Френсиса. (см.рис.26)
В отличии от работающей на воздухе турбины Пельтона, турбины Френсиса должны быть всегда полностью затоплены, а потому они всегда работают всеми лопатками сразу.
Постоянная погружённость в воду турбины Френсиса позволяет использовать её как в качестве турбины генератора в прямом режиме, так и в качестве рабочего колеса насоса при обратном направлении вращения ротора, когда осуществляется обратная закачка воды из пруда-аккумулятора обратно в водохранилище.
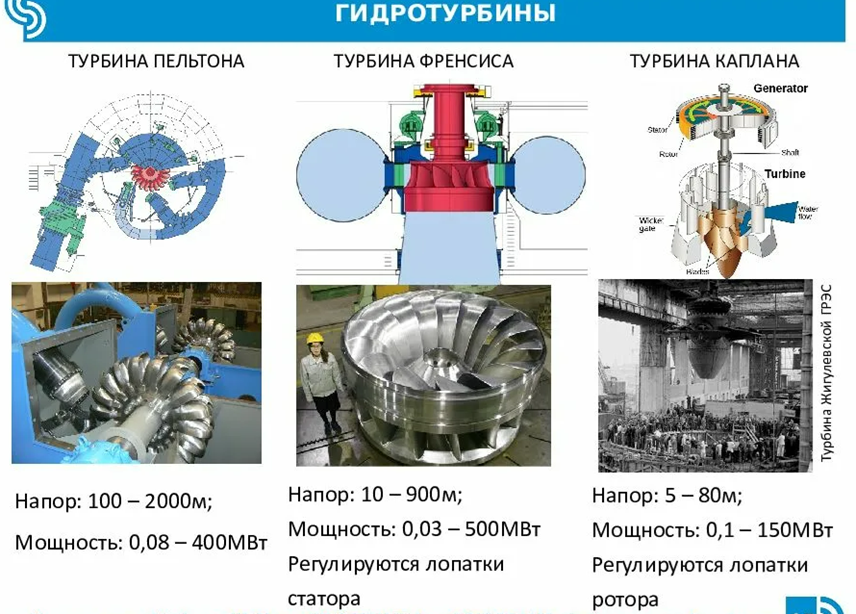
Рис.26. Турбины разных типов для ГЭС и граничные условия их применения.
Турбины с косым входом струи на рабочее колесо.
Кроме турбин Пельтона, где вход струи находится в плоскости вращения турбины, существуют ещё и турбины с косым входом потока на лопатки турбины.
Такие турбины для воды называют «Наклонно-струйные гидротурбины» (см.рис.27)
Для газообразного рабочего тела ( в том числе водяного пара) также используют турбины с косым входом струи на лопатки турбин.(см.рис.28-30)
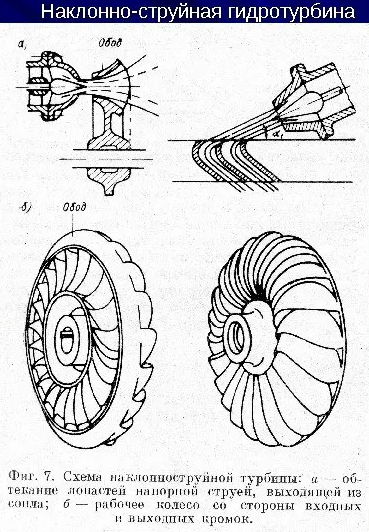
Рис. 27. Наклонно-струйная турбина: а-Схема подачи струи на лопатки турбины, Б- общий вид турбины с разных сторон.
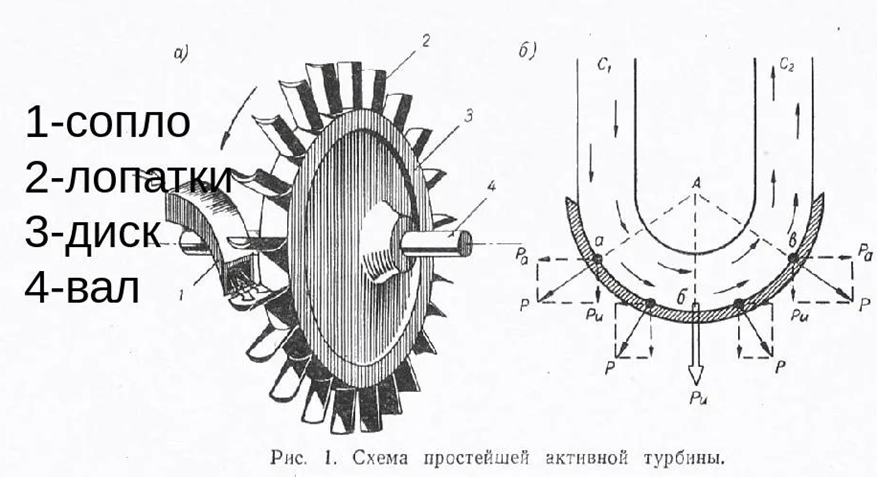
Рис. 28. Вид простейшей одноступенчатой односопловой активной турбины, какими пользовались как для водяного пара, так и для воды в позапрошлом 19 веке.
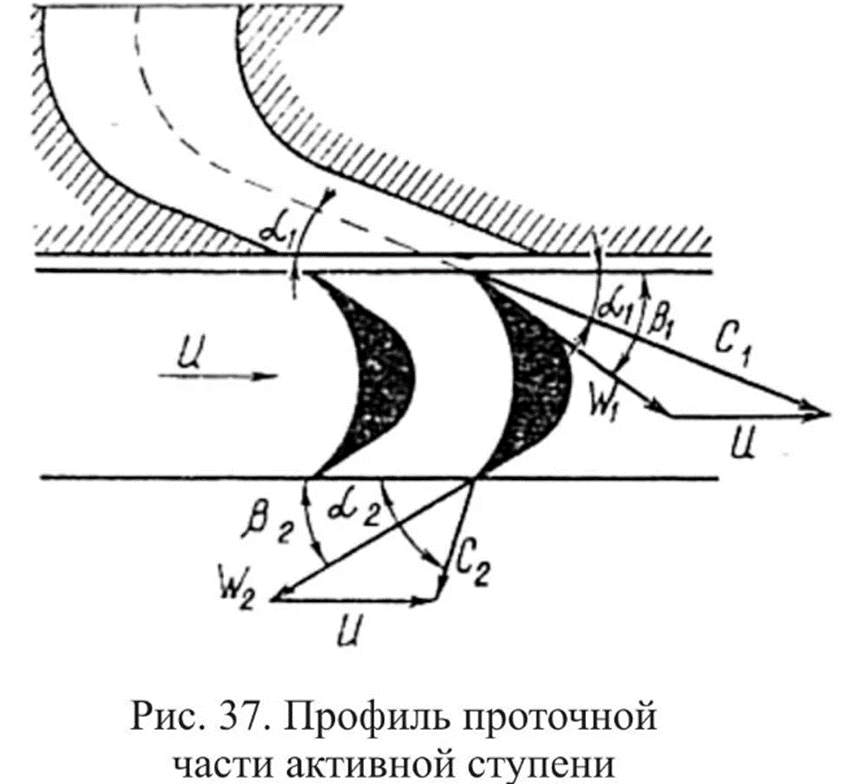
Рис. 29. Векторная схема скоростей на лопатках наклонно-струйной турбины.
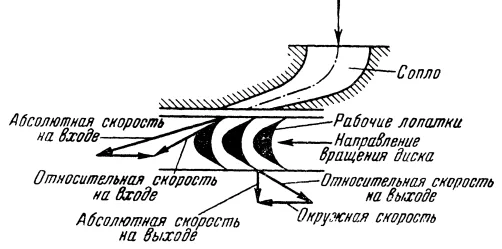
Рис. 30. Векторная схема скоростей на лопатках наклонно-струйной турбины. Со словесными расшифровками значения векторов.
Газовые турбины вынуждены использовать несколько каскадов наклонно-струйных турбин с малыми углами поворота потока, так как газы легко сжимаемы и не могут в одну ступень отдать всю внутреннюю энергию в кинетическую энергию скоростной струи.
В теории за один цикл одна ступень газовой турбины способна снять около 30% имеющейся внутренней энергии газа, содержащейся в газе на момент входа в разгонное сужение направляющего сопла (то есть не более 1/3 общей внутренней энергии газа, приходящейся на одно направление).
Правда, всю энергию нельзя снять с газа за три ступени турбины, так как вторая ступень турбина снимет те же 30%, но уже от остатка в 70%. В итоге получается бесконечная дробь, асимптотически стремящаяся к нулю при количестве ступеней стремящемся к бесконечности.
В итоге снять 90% энергии газа (остаток менее 10%) будет возможно лишь на каскаде из 7 ступеней:
(1-0,7^7)*100=(1- 0,082)*100=91,7%
При этом ряд из 10 ступеней турбин даст выход 97,2 % или прибавку всего в 6%:
(1-0,7^10)*100=(1- 0,028)*100=97,2%
Интересно, что для идеальной газовой турбины КПД 99% достигается при каскаде из 13 ступеней (см.рис.33)
То есть каждый последующий ряд турбины даёт всё меньшую прибавку суммарной мощности.
Так же важно учитывать, что последние ступени много больше по габаритам и значительно дороже, чем первые ступени (см.рис. 32).
Таким образом, каждый следующий ряд газовой турбины нужно экономически обосновывать, сравнивая стоимость добавочной выработки энергии с добавочной ценой каждого лишнего каскада.
Реальные КПД газовых турбин, использующих продукты г орение топлива в воздухе, ограничено диапазоном 30-42%, то есть лучше бензиновых ДВС (КПД 25%) и хуже, чем большие судовые дизельных ДВС (КПД до 50%).
Объясняется низкий КПД газовых турбин тем, что невозможно принять на лопатки турбины газы с температурой 2500С из-за плавления металла лопаток. В итоге в современных газовых турбинах рабочий горячий газ приходится разбавлять холодным воздухом до приемлемых 800-1000С. Также практически невозможно выхолодить газ ниже температуры окружающей среды в 300К (+27С).
Вот и получается бесполезная потеря 60-70% температурного диапазона газов.
У паровых турбин КПД тоже около 30-35%, хотя температура пара всего +500С. Но это вина уже не турбины, а неизбежного зла парового цикла: «энергии конденсации водяного пара».
Так в замкнутом цикле рабочего тела «энергия конденсации» (которую сбрасывают на градирни) превышает всю ту полезную энергию, которая вырабатывается на турбине в цикле от парового котла на входе до конденсатора на выходе.(см.рис.34)
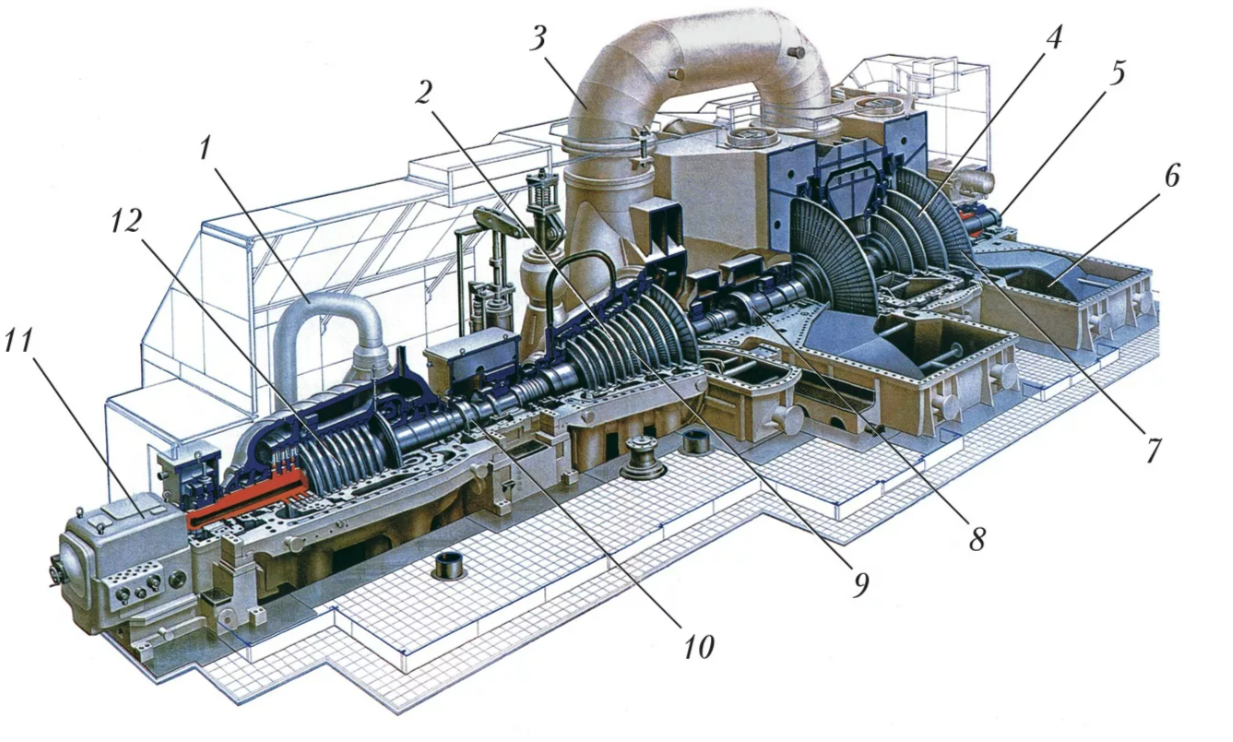
Рис. 31. Разрез паровой турбины с тремя блоками турбин: 12- Турбина высокого давления (влажный пар), 2- Турбина среднего давления (перегретый пар после теплообменника- перегревателя), 4-Турбина низкого давления (после неё температура пара всего +42С). 1- Отбор влажного пара после первой ступени на теплообменник– перегреватель. 3-Паропровод с температурой около +160С (именного с него на ТЭЦ отбирают пар для подогрева сетевой воды до +150С на отопление города, когда потребность в электроэнергии от ТЭЦ падает до уровня ниже 80% от её номинальной мощности). 6- отбор пара стемпературой +42С и давлением 1% от атмосферного на конденсацию в теплобменниках при помощи охлаждающе воды с графиком +30/35.

Рис. 32. Ротор 5-ти ступенчатой паровой турбины низкого давления . Видно на сколько лопатки на первой ступени меньше, чем на пятой. Ступени высокого давления к этой турбине добавляют отдельным блоком на той же оси.

Рис. 33. Моноблочная 13-ти ступенчатая паровая турбина. Видно, что лопатки на первой ступени в несколько раз меньше, чем на последней 13-той ступени.

Рис. 34. Градирни на ТЭЦ в г.Москве, из которых идут клубы водяного тумана (широкие трубы с синим верхом на переднем плане, и бетонно-серые на заднем плане). В них происходит сброс тепла в атмосферу от охлаждающей воды конденсаторов паровых турбин, при этом температура входящей охлаждаемой воды всего +35С. Узкие и высокие красно-полосатые трубы- это дымоходы от паровых котлов ТЭЦ. В жаркие дни дым над дымовыми трубами может быть не виден вовсе, так как в сухом тёплом воздухе выхлопы из котла остывают не сразу, а потому невидимый водяной пар в видимый туман сразу не выпадает, при том что видеть мы можем только сконденсировавшийся холодный туман. На горизонте справа на фото видны небоскрёбы Москва-Сити.
Интересный видеоролик с пролётом турбовинтового самолёта в жарком и сухом аравийском воздухе, где за самолётом не появляется привычный «дымовой» след от его турбо-винтовых двигателей. (см.видео)
dzen.ru/video/watch/64c68a149ab9276d36a64f22
Как альтернатива: В переувлажнённом воздухе конденсат выпадает во всём объёме воздуха за самолётом, тем самым визуализируя масштабное аэродинамическое явление в процессе реального полёта, и даже лучше чем дымами в АДТ.
dzen.ru/video/watch/63badf7a0f646d4b9a595f89
Реальный параметры паровых турбин
Для паровых турбин на ТЭЦ ограничения по эффективности отдельного каскада турбины ещё жёстче, чем для газовых турбин на продуктах воздушного горения топлива.
Максимальный разгон в сужающемся разгонном сопле для газа ограничен скоростью звука в газе при данной температуре. Для перегретого пара с температурой +500С (как на ТЭЦ) максимальная скорость потока составит около 800м/с, а скорость лопаток одноступенчатой турбины должна была бы быть 400м/с.
Но в реальных паровых турбинах на ТЭЦ окружные скорости для турбин ограничены несколькими факторами:
1. Угловой скоростью электрогенератора при прямом вращении от вала турбины ( 50Гц= 50об/с=3000об/мин),
2. Допустимыми окружными скоростями лопаток из-за предела прочности материала на растяжение из-за центростремительного ускорения.
При диаметре турбины 1м на частоте 50Гц окружная скорость на ободе турбины составит V=50*3,14*1=157м/с.
Таким образом, даже очень крупная по диаметру первая ступень паровой турбины не способна в одну ступень сработать в ноль максимальную скорость пара, вылетающего из разгонного сопла.
Таким образом, получается, что при срабатывании по одной трети от максимальной скорости перегретого пара для снятия 30% общей энергии потребуется даже не 3 ступени (как казалось бы), а 9 ступеней (квадратичная зависимость энергии от скорости).
Именно этим объясняется такое большое количество ступеней в первом каскаде высоко давления паровой турбины ТЭЦ (см.рис.31)
С точки зрения прочности лопаток тоже есть серьёзные ограничения.
Так для той же турбины диаметром 1м центростремительное ускорение составит
a=V^2/R=157^2/0,5=49300 м/с^2 ( или 5 тыс. g)
Для лопатки из стали плотностью q=8000кг/м3 и высотой лопатки h=0,1м при таком ускорении возникнут разрывные напряжения
Р=a*h*q=49300*0,1*8000=40Мпа
А ведь есть ещё и не малые изгибные напряжения в лопатках!
С учётом коэффициента запаса прочности Кз=5 получается, что расчётное напряжения для материала лопаток Рм=5*40=200МПа, а это уже близко к пределу длительной прочности легированной жаропрочной стали 150-250МПа.
Турбодетандер Капицы
Если в горячей энергетике повсеместно используются многоступенчатые турбины, то в при работе с холодными газами ситуация иная. Так в криогенной технике (то есть при предельно низких температурах), существуют вполне себе одноступенчатые газовые турбины- турбодетандеры. (см.рис.35-36)
По исполнению полузакрытые турбины турбодетандеров очень похожи на гидротурбины Френсиса, но работающими с холодными сжатыми газами. (см.рис.37-40). Именно этими идеями о схожести переохлаждённых газов с водой руководствовался Пётр Капица в 1938 году при модернизации имевшихся тогда турбодетандеров.
Задачей турбодетандеров является снятие энергии сжатого газа так, чтобы после декомпрессии газ не имел бы высокой скорости в трубе.
Турбодетандеры используют в газовой промышленности для перевода газа из транспортных магистралей высокого давления 12 атм (от месторождения до района потребления) к распределительным магистралям низкого давления (0,05 атм избыточного давления или 1,05 бар абсолютного)..
То есть давление в газовых трубах может снижаться в 12-13 раз.
В качестве нагрузки для таких турбодетандеров устанавливают электрогенераторы, которые трансформируют энергию сжатого газа в электроэнергию.
Также турбодетандеры применяют в процессах сжижения газов, например, для выделения кислорода из воздуха в металлургической промышленности.
На турбину криогенного турбодетандера изначально подаётся сильно охлаждённый газ с температурой до минус 130С (143К). При такой температуре скорость звука в воздухе составляет 234м/с, а это уже даёт вполне достижимую скорость в 120-150 м/с для лопаток турбины. При этом сама турбина также не имеет ограничения по угловой скорости, так как она не ограничена частотой тока 50 Гц.
Для криогенного турбодетандера в качестве нагрузки подключают соосный блок турбокомпрессора, сжимающий свежи воздух на подачу к сжижающей установке. При этом турбокомпрессору тоже нужны высокие скорости вращения, как и для турбодетандера.
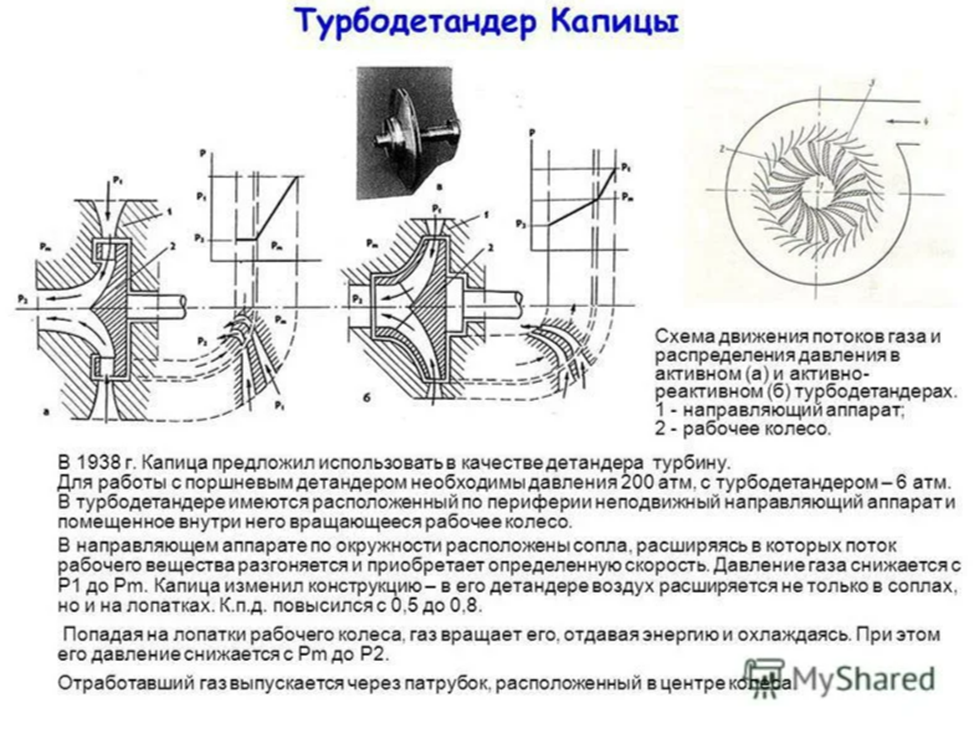
Рис.35. Разрезы турбодетандеров разных типов: А- с обычной однорядной турбиной, Б- турбина Капицы с расширяющимися и вращающимися с турбиной соплами позади рабочих лопаток турбины.

Рис.36. Рабочее колесо турбодетандера Капицы.


Рис.37. Сравнение 3-д моделей рабочих колёс турбин: А-Рабочее колесо турбодетандера полуоткрытого типа (современная 3-д модель). Б- гидротурбина Френсиса для ГЭС

Рис.38. Рабочее колесо гидротурбины Френсиса .
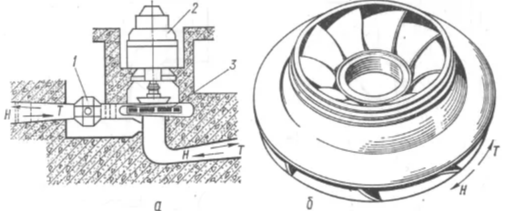
Рис.39. Радаильно-осевая турбина Френсиса: А- в составе реверсивной ГЭС, Б- рабочее колесо турбины, очень похоже на закрытое колесо турбодетандера Капицы.
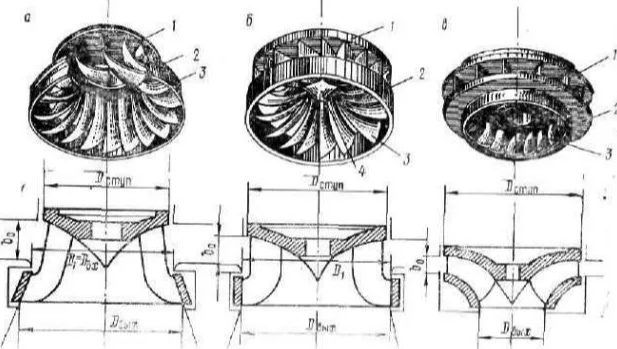
Рис.40. Радиально-осевая турбина Френсиса с различным отношениями расход/напор: А- низконапорное колесо турбины, Б- средненапорное рабочее колесо турбины, В-высоконапорное рабочее колесо турбины (очень похоже на закрытое колесо турбодетандера Капицы).
Заключение
В результате проведённого анализа становиться видно, что для реальных явлений в реальной жизни «Идеальная жидкость» не применима как физическая модель.
Применение «Идеальной жидкости» в составе «Уравнения Бернулли» никак не способно объяснить реальное протекание физических процессов в «Гидравлике», а лишь плодит абсурдные «парадоксы».
В тоже время физическая модель «Изгибания потока под действием центростремительных давлений» даёт вполне адекватное описание реально существующих физических процессов и явлений, таких как «подъёмная сила крыла» и «поперечное давление в повороте трубы». Также эта модель даёт адекватное объяснение поведения «Вертушки Фейнмана» при изменении направления потока в ней с разбрызгивания на всасывание.
Комментарии (92)

kbtsiberkin
05.09.2023 16:53+12Шли десятилетия и века. И вот в 20-м веке возникла мода на «теоретическую науку», где стали исследовать отвлечённые физические модели со свойствами, сильно отличающимися от реальных объектов и субстанция.
Ну это зря, конечно. Идеальная жидкость — это Бернулли, 1730е гг., и Эйлер, 1750е гг. А вязкая жидкость — Навье, Стокс, Пуассон и др. — 1820е. И сходу заявлять что‑то в духе «наука это всё фигня, вот то ли дело реальная инженерия!».
В идеальной жидкости, понятно, далеко не всё учтено, однако во многих простых ситуациях уравнения Эйлера вполне прилично работают. Аэродинамика тоже во многом для идеальной жидкости написана. Теорема Жуковского о подъёмной силе, например. На базе которой прекрасно строится теория профилей крыльев и винтов. Просто учёт вязкости штука чрезвычайно противная, как минимум. И иногда легче описать вязкий пограничный слой и сопряжённое ему идеальное течение вдалеке от границы.
Современная же жизнь в разработке турбин, компрессоров и двигателей давно уже не обходится без вязких моделей, благо на помощь пришли хорошие мощные мат.пакеты типа ANSYS, OpenFOAM и иже с ними. Но базовая инженерная эмпирика, конечно, во многом была найдена без них. Из приемлемо работающих в большинстве условий моделей идеальной среды.

iMonin Автор
05.09.2023 16:53-5Никакой теории профиля крыла не строится с использованием ни теорий Жуковского , ни уравнений Бернулли.
Именно эти люди не имеют никакого отношения к реальному моделированию "подъёмной силы крыла". При этом ссылками на их "авторитеты" лишь прикрывают повторения изживших себя "идеальных" моделей, которыми забиты первые десятки и сотни страниц профильных учебников.
Без вязкости в принципе рассыпается вся модель реальной жидкости, так как "идеальная" жидкость не умеет тормозить.
Наука- это тонкая грань между обыденным из учебников и НЕВЕДОМЫМ за гранью общеизвестного!
За науку практически не платят, так как невозможно предсказать кому, когда и как удастся прорваться за эту грань и насколько далеко.
Ну, а Пересказ учебника студентам за зарплату- это всего лишь Преподавание, а не Наука.

kbtsiberkin
05.09.2023 16:53+7Никакой теории профиля крыла не строится с использованием ни теорий Жуковского, ни уравнений Бернулли.
Таки странно. Куда ни ткни — циркуляцию считают. А раз циркуляция, значит — Жуковский. А раз Жуковский — значит, Бернулли, одна теорема из другой вытекает.
Но, судя по предшествующим заметкам — «Объяснение физической сущности явления „Подъёмная сила Крыла“ без использования уравнения Бернулли» (часть 1 и часть 2) — автора в этом не переубедить.
Единственный вопрос возникает — что ж так, и вас лобби академиков не пускает в профильные издания публиковаться, и потому приходится писать псевдонауку на хабре?

iMonin Автор
05.09.2023 16:53-5Куда ни ткни они только ГОВОРЯТ, что считают какую-то циркуляцию!
По факту же ничего они не считают, так как вся эта теорема Жуковского- это случайная мысль старого профессора, которую бездумно разрекламировали и растиражировали его бездарные ученики.
Реальные авиаконструкторы никакие циркуляции ротора по профилю крыла не считают...)))

RigidStyle
05.09.2023 16:53-1Я помню мы как то всем селом (в купе с конструкторами) спорили, почему летает дельтаплан. У него переменный угол атаки, если вдруг кто не знает, и получается, что у него среднее значение угла атаки положительное. Но когда мы берем планер с подожительным углом атаки, то рано или поздно он остановиться, и после свалиться. В теории. А на практике он летит на положительном угле атаки. Еще и управляется. Ну проще всего представить лист бумаги или фанеры, если его тупо отпустить, то он начнет движение в ту сторону, в которую наклонен. Так вот у дельтаплана " та сторона" - это назад (из за результирующего положительного угла атаки). Но летит он вперед. Выдвигались множество теорий, и про парашютирование управляемое, и про цт, который в сумме со стреловидностью дает такой эффект. Но суть в том, что дельтаплан летает вопреки известной теории.

iMonin Автор
05.09.2023 16:53Обычное заблуждение при неточности определений.
Положительный угол атаки вы как определяете?
Какой угол считается нулевым углом атаки?
Если рассматривать симметричный профиль крыла планера, то его планирование всегда идёт на отрицательных углах крыла к К ГОРИЗОНТУ!
А вот к вектору скорости ( к траектория снижения) будет положительный угол.
При несимметричном профиле вообще непонятно какой угол чем считать.

mayorovp
05.09.2023 16:53+1Но когда мы берем планер с подожительным углом атаки, то рано или поздно он остановиться, и после свалиться.
Это не может быть правдой хотя бы по той причине, что нулевая точка угла атаки выбирается, по сути, произвольно.

mayorovp
05.09.2023 16:53+15Что-то я прочитал это всё три раза, и так и не понял с какими такими ветряными мельницами борется автор.
Разумеется, любая формула применима пока соблюдаются условия её применения. Конкретно для формулы Бернулли поток жидкости должен быть стационарным, не терять много энергии на трении, и быть именно такой формы какой был нарисован. Если формула привела к парадоксу — значит, что-то из этих предположений оказалось неверным, только и всего.
Что дальше? Ждём разоблачение закона Ома, с примерами в виде различных стабилизаторов и прочих преобразователей напряжения? (У них потребление тока растёт при падении напряжения, если кто не понял в чём тут юмор)

kbtsiberkin
05.09.2023 16:53+3Судя по предыдущим публикациям автора, может и такое что-нибудь появиться :)

konst90
05.09.2023 16:53+5Если формула привела к парадоксу — значит, что-то из этих предположений оказалось неверным, только и всего.
Шмель по законам аэродинамики летать не должен, да.

iMonin Автор
05.09.2023 16:53-2Если шмель летает, то надо всерьёз уже разобраться с той "Аэродинамикой", по которой он летать не может...)))

konst90
05.09.2023 16:53+8Да с ней уже давно разобрались, модели полёта шмеля существуют.
История эта про шмеля тянется из тех времен, когда его попробовали посчитать по формулам для самолётов. Ожидаемо - оказалось, что шмель не самолёт и летает как-то иначе. Но почему-то это стало мемом.

iMonin Автор
05.09.2023 16:53+1Да, я знаю...)))
Но именно этот старый мем и многие подобные должны подталкивать современных преподавателей к пересмотру шаткого базиса под толстыми, но ничего толком не объясняющими учебниками...

EugeneH
05.09.2023 16:53+2Ни к каким парадоксам уравнение Бернулли, конечно же, не приводит. И выводится оно напрямую из уравнений Навье-Стокса, если принять некоторые допущения.
Никаких проблем идеальная жидкость не испытывает, послушно ускоряется в сужениях канала и тормозится, пройдя расширение.
Более того, с его помощью можно преспокойно рассчитывать и движение вязкой жидкости - с учетом потерь энергии между сечениями.
Можно рассчитать и нестационарное течение - вводится дополнительный член, т. н. "инерционный напор". Этого инструментария вполне достаточно, чтобы, например, на коленке посчитать минимально допустимое время закрытия (максимальную скорость) направляющего аппарата гидротурбины, чтобы не возникло недопустимого разрежения в камере рабочего колеса.
Но вот к течению пара в проточной части паровой турбины оно не имеет никакого отношения, т. к. для газов нельзя пренебречь сжимаемостью. Для потока газа есть похожее уравнение полной энтальпии.
Я вот буквально сейчас занят вводом в строй энергоблока 360 МВт на сверхкритическом паре и почти больно читать, когда кто-то с серьёзным видом пишет про "дно котла" и что не может быть перегретого пара на входе ЦВД, но это уже ниже отметили. Всё же надеялся, что после разгрома теории Жуковского и модели атомного ядра, автор низвергнет Эйнштейна или хотя бы квантовую механику.

iMonin Автор
05.09.2023 16:53-1Уравнение Бернулли - это простенькая запись закона сохранения энергии для двух соседних сечений одной труб с единым расходом. К уравнениям Навье-Стокса оно не имеет никакого отношения, так как Бернулли умер много раньше, чем эти парни родились.
Для продольной по потоку энергии УБ вполне применимо, так как это просто Закон сохранения энергии. Но как оно определяет давление на стенку трубы в повороте???
Да, для газов всё сложнее из-за сжимаемости.
Обсуждение нюансов котлостроения на ТЭС-ТЭЦ не тема этой статьи. Единственное упоминание мной котла относится к энергии конденсации, из-за которой КПД паровых турбин сильно меньше 30% без многоступенчатого перегрева.
Дно у котла есть всегда: там закачивают холодную воду. Ну и заканчивается низ котла где-то на границе раздела сред пар-вода, или где по температуре пропадает граница жидкость -газ. Вообще в трубчатых котлах всё это размыто.
Эйнштейна и квантовую механику я низвергать не буду, так как они отомрут и без моего участия. Я занимаюсь реальным сектором в физике, где эксперименты возможны и полезны без строительства бессмысленно-гигантских суперколлайдеров...

Daddy_Cool
05.09.2023 16:53"т. к. для газов нельзя пренебречь сжимаемостью".
Маленькое уточнение. Нельзя пренебречь сжимаемостью пара при имеющихся в турбине скоростях.

mayorovp
05.09.2023 16:53+6Теперь пройдёмся по вашим "парадоксам".
Основная причина противоречий ИЖ с реальностью состоит в том, что каким-то загадочным образом удаётся свободно трансформировать потенциальную энергию давления в кинетическую энергию и обратно без потерь и без применения дополнительных механизмов.
В уравнении Бернулли нет ничего про отсутствие механизмов. В конце концов, труба такой же механизм для направления потока жидкости, и невозможность одной только трубой добиться стационарного расширяющегося потока — ограничение не уравнения, а механизма "труба".
Если же просто продлить логику УБ для ИЖ, то получится, что при расширении потока давление должно как-то само увеличиваться за счёт уменьшения кинетической энергии при падении скорости потока.
"Само собой" тут лишнее. Очевидно, что повышенное давление нужно отдельно прикладывать, и именно оно и замедляет жидкость.
То есть идеальная струя ИЖ из-за своей идеальной скользкости не заметит расширения трубы, а будет проскальзывать сквозь покоящийся объём ИЖ в расширенной трубе так, будто продолжает течь по прямой трубе постоянного сечения.
Тут покоящийся объём жидкости надо заменить на газ и всё встанет на свои места.
Этот "парадокс" лично я наблюдал кучу раз на кухне и в ванной. Открываю кран — и вода начинает течь из крана тонкой струйкой вместо того чтобы заполнить комнату (="трубу большего сечения") целиком.
Четвёртым противоречием УБ и его применения вне замкнутой твёрдой трубы является то, что в УБ никак не рассматривается динамика потока на изгибах стенок трубы (при поворотах или изменении сечения).
И не должна. Уравнение Бернулли применяется к потоку, а не к трубе. Чтобы применить его к изогнутой трубе (особенно к крутоизогнутой), надо сначала выяснить как именно вода будет по этой трубе течь, со всеми этими закручиваниями, потом выделить кусок потока, ограниченный траекториями условных частиц воды, и уже к нему можно применить уравнение.
В тоже время одинаковое дополнительное центростремительное избыточное давление на внешней стенке поворота трубы будет создаваться как при сложном распределении скоростей по сечению, так и при постоянной скорости потока по сечению струи.
А эта самая постоянная скорость потока по сечению струи — она вообще для изогнутого потока в принципе возможна? Что-то мне так не кажется.

iMonin Автор
05.09.2023 16:53-4УБ для ИЖ рассматривает элементарную "трубочку-струю", в которой уже не может быть никаких вихрей. То есть все механизмы торможения жидкости на расширении элементарного потока уже должны быть описаны.
А откуда возьмётся это повышение давления для торможения жидкости? Каков его механизм реализации?
Жидкость "по-бернулли" внутри жидкости течёт- это "затопленная струю". Так причём тут струя из крана на воздухе?
Да, я это влияние поворота на поток жидкости в трубе я и выяснял. В уравнении Бернулли про загибы труб нет ни слова, именно по этому УБ не применимо ни для Аэродинамики с авиастроением, ни для Гидродинамики с судостроением.

mayorovp
05.09.2023 16:53+4УБ для ИЖ рассматривает элементарную "трубочку-струю", в которой уже не может быть никаких вихрей. То есть все механизмы торможения жидкости на расширении элементарного потока уже должны быть описаны.
УБ для ИЖ рассматривает элементарную "трубочку-струю" как данность, никак не касаясь вопроса каким образом эта самая "трубочка-струя" вообще образовалась.
А откуда возьмётся это повышение давления для торможения жидкости? Каков его механизм реализации?
А это и надо придумать чтобы получить расширяющийся стационарный поток без потерь.
Жидкость "по-бернулли" внутри жидкости течёт- это "затопленная струю". Так причём тут струя из крана на воздухе?
Она может течь внутри чего угодно до тех пор пока выполняются условия применимости.
Да, я это влияние поворота на поток жидкости в трубе я и выяснял. В уравнении Бернулли про загибы труб нет ни слова, именно по этому УБ не применимо ни для Аэродинамики с авиастроением, ни для Гидродинамики с судостроением.
Всё ещё не вижу как из "про загибы труб нет ни слова" следует "УБ не применимо".

iMonin Автор
05.09.2023 16:53-7Да, совершенно верно!...Это и есть основная претензия к УБ для ИЖ...))...То есть они очень тщательно исследуют некий абстрактный предмет, которого не существует, то есть "сферического коня в вакууме"...)))
Без потерь поток не тормозится, так как этому препятствуют законы РЕАЛЬНОЙ Физики...
Затопленная струя внутри потока жидкости и струя в комнате из крана- это ни разу несовпадающие обстоятельства, чтобы их как-то друг на друга подменять.
Во всех случаях Гидравлики в судостроении и Аэродинамики в авиации рассматриваются именно поперечные давления в изогнутых потоках воздуха или воды, а именно эти давления никак в УБ и не рассматриваются. Вот почему УБ бесполезно везде, кроме водопроводных труб.

mayorovp
05.09.2023 16:53+3Затопленная струя внутри потока жидкости и струя в комнате из крана- это ни разу несовпадающие обстоятельства, чтобы их как-то друг на друга подменять.
При условии пренебрежимо малых потерь они друг с другом совпадают.
Да, струя из-под крана гораздо чаще оказывается в условиях когда потерями можно пренебречь, однако, в конце концов, это вопрос исключительно требуемой точности.
Во всех случаях Гидравлики в судостроении и Аэродинамики в авиации рассматриваются именно поперечные давления в изогнутых потоках воздуха или воды, а именно эти давления никак в УБ и не рассматриваются. Вот почему УБ бесполезно везде, кроме водопроводных труб.
Давление в жидкостях распространяется во все стороны одинаково, закон Паскаля никто не отменял.
Или вы хотите сказать, что закон Паскаля тоже пора выбросить на свалку, как и уравнения Навье-Стокса?

iMonin Автор
05.09.2023 16:53-3Если бы воздух имел равную плотность с водой, то я бы мог и согласится с вашей аналогией. Но пока же ваша "аналогия" не просто хромает, а глубоко мертва.
Я не просто так вам привёл пример стакана с водой на столе или на центрифуге! В обычном стакане воды в гравитационном поле давление НЕ ОДИНАКОВО по разным направлениям!...Так что закон Паскаля- это ни разу не закон, а просто наблюдение для некоторых конкретных систем при весьма существенных граничных условиях..

mayorovp
05.09.2023 16:53+2В обычном стакане воды в гравитационном поле давление НЕ ОДИНАКОВО по разным направлениям!...
Одинаково. Вы путаете зависимость давления от положения и от направления. Первая зависимость существует (и учитывается в формулах), второй зависимости нет.
Тот факт, что давление отличается в зависимости от высоты, ещё не означает что "давление вверх" отличается от "давления вбок".

iMonin Автор
05.09.2023 16:53-3Конечно отличается!
Иначе как будет меняться давление по высоте стакана?
Давление вбок и давление по вертикали разные, так как разные направления приложения сил между взаимодействующих молекул.
Вы копнули правильную проблему, так как в теории сплошных сред как-то забывают, что среды вовсе не "сплошные", а состоят из твёрдых атомов и молекул, между которыми есть силовые взаимодействия.
Если в качестве объекта среды рассматривать не абстрактный упругий "кисель твёрдого тела", а конкретный твёрдый и массивный шар атома во взаимодействии с такими же шарами атомов вокруг, то проблема изменения давления вокруг одиночного шара сразу решается.
Так сверху атома будет приложена удельная сила "давления" от выше лежащих масс атомов.
А вот вниз атом будет давить сильнее, чем вверх, так как в "давление" вниз он добавит и собственный вес.
Давления в бок вообще могут быть любыми, так в состояниях быстротекущих процессов удержание бокового равновесия не требуется, так как малость времени протекания скоротечного акта не позволяет атомам далеко уйти от положения равновесия даже при отсутствии сил поперечной балансировки слоя.

mayorovp
05.09.2023 16:53+2Удачи вам в моделировании отдельных атомов, но обычно всё-таки люди моделируют жидкость. Даже практики. Особенно практики.

iMonin Автор
05.09.2023 16:53-2Люди ПОЛЬЗУЮТСЯ водой из под крана, ни разу не задумавшись над распределением давления в трубе и падении давления на самом кране.
Ну, а вопрос изменения давления между отдельными атомными слоями- это вопрос сугубо для теоретиков, так как сами отдельные атомы просто невозможно наблюдать.
Быстротекущие процессы вообще плохо наблюдаемы, а потому их постоянно пытаются изобразить как "квази стационарные процессы", тем самым запутывая себя и незаметно видоизменяя сам объект изучения.

konst90
05.09.2023 16:53+2Иначе как будет меняться давление по высоте стакана?
Как функция от высоты водяного столба для данной точки.
Гидростатическое давление не зависит от вектора приложения силы и при равной высоте водяного столба одинаково.
Как практик скажу, что в случае давления моделирование отдельных атомов никому не интересно. Мне при расчёте сосуда важно знать силу, которая приложена к узлам конечных элементов - то есть её величину и вектор (вернее, даже это мне знать не надо, я указываю силу тяжести, плотность жидкости и положение плоскости поверхности жидкости, а силу на конечные элементы ANSYS раскидывает сам). И вот эта сила от ориентации конечного элемента не зависит.
В динамике всё сложнее, но и там при прочностном расчёте к поверхности прикладываются поля давлений (которые опять же ), а не воздействия отдельных атомов. И эти поля опять же раскидываются как силы, приложенные к конечным элементам исходя из их площади.

iMonin Автор
05.09.2023 16:53-3Я с вами СОГЛАСЕН!!!...)))
Только вы говорите о математической зависимости для "идеальной жидкости", а я говорю о сути самого РЕАЛЬНОГО явления.
В вашей версии вода не имеет атомов и бесконечно дробима.
В моём случае мы доходим до конкретного материального твёрдого атома, который сам по себе уже не является жидкостью, но эту жидкость формирует своими пограничными свойствами.
Именно на уровне твёрдого атома можно легко объяснить как вдруг давление в округ этого твёрдого атома может быть разным по направлениям.
Как пример- куча песка, которая вроде как давит на грунт всей массой, но друг на друга песчинки давят весьма неодинаково, формируя локальные концентрации напряжений и локальные разгруженные участки(даже с пустотами).
Из-за этого "песчаного"эффекта зерновые элеваторы иногда рушатся (криво сминаются вбок), так как весь вес зерна случайно (на короткие мгновения при опорожнении снизу) повисает на стенках, которые такую вертикальную нагрузку выдерживать просто не должны ( оболочки стальных элеваторов считают на растяжение)..

Daddy_Cool
05.09.2023 16:53+2>в теории сплошных сред как-то забывают, что среды вовсе не "сплошные", а состоят из твёрдых атомов и молекул, между которыми есть силовые взаимодействия.
Так на то она и модель сплошной среды с известными границами применимости, а вы о быстротекущих процессах. Пожалйста, сделайте оценки типичных времен этих процессов и скажите, ну... скажем, с какой скоростью должен лететь самолет, чтобы неправильная модель сплошной среды давала существенные отличия от правильной молекулярно-кинетической теории.
iMonin Автор
05.09.2023 16:53-2Так кто вам сказал, что "молекулярно-кинетическая теория" является правильной?
В ней-то концы с концами как раз и не сходятся!
По мне так теория сплошных сред для воздуха куда более применима, только среда должна ещё и течь при этом, не забывая о центростремительных ускорениях для отдельного элементарного кусочка массивной "сплошной среды"...)))

mayorovp
05.09.2023 16:53-1Тогда замените "молекулярно-кинетической теорию" на любую другую, которую лично вы считаете правильной, и всё-таки дайте оценку.

potalaizer
05.09.2023 16:53Справедливости ради, закон Паскаля всё же работает, если верить Википедии:
Следует обратить внимание на то, что в законе Паскаля речь идет не о давлениях в разных точках, а о возмущениях давления, поэтому закон справедлив и для жидкости в поле силы тяжести.

iMonin Автор
05.09.2023 16:53-3Возмущения давления- это ВОЛНЫ, а они вообще ни разу не статичны, а быстро бегут от атома к атому.
Так что "закон Паскаля"- это не закон, а всего лишь наблюдение для стационарной ситуации в статичной системе, да и то ошибочно сформулированное.
Про быстротекущие процессы и про разнонаправленные давления при них я ответил чуть выше.

Matshishkapeu
05.09.2023 16:53+5Можно ещё принести с собой пенопластовое ведёрко жидкого азота и, ударяя себя пяткой в грудь, клеймить позором теоретических учённых типа всяких Гей-Люссаков за модель идеального газа.

Radisto
05.09.2023 16:53+1Можно вопрос от дилетанта? А каким образом запускается турбина пельтона? Ведь в самом начале она неподвижна, а в ее лопатки бьет поток на скорости выше 300 км/ч, и отражаясь, он должен неплохо так орошать кожух, который вроде не рассчитан на давление. Или турбину заранее раскручивают без воды?

iMonin Автор
05.09.2023 16:53Вы правильно заметили про брызги.
Да , именно от брызг, в том числе пусковых, кожух и защищает.
Но проблема пусковых брызг не так уж страшна, если учесть, что разгоняют турбину без нагрузки, то есть очень тонкой струёй.
И только на номинальной частоте вращения к турбине постепенно подводят нагрузку от генератора с таким же постепенным наращиванием мощности струи.
Регулятор сопла не случайно изображён на всех картинках.

Oedo
05.09.2023 16:53+2Рис. 31.
Турбина высокого давления - по русски говорят цилиндр высокого давления или ЦВД. И далее ЦСД, ЦНД.
(влажный пар)
Цикл Ренкина для посмотрите, там почему-то перегретый. Справедливо сказать насыщенный пар для некоторых АЭС.
теплообменник– перегреватель
Ваш ChatGPT cмешал в кучу комментарии к картинкам ТЭС и АЭС. На ТЭС перегрев пара происходит в промежуточном перегревателе в самом котле, на АЭС - в сепараторе-пароперегревателе.
В результате проведённого анализа становиться видно,
что инженерам, разрабатывающим системы и оборудование для реальных сред, никогда в голову не придёт рассматривать течение идеальной жидкости, т.к. потери наше всё, а "гидравлику" в ВУЗе просто сдают.
Разбирать все опечатки для фактов, малоприменяемых в настоящее время долго.
Статья, как набор фактов для развития кругозора студентов машиностроительного вуза, вполне сойдёт.

iMonin Автор
05.09.2023 16:53Согласен.
-
Сразу из котла перегретого пара быть не может, так как на дне котла ещё есть жидкая вода. Перегретый пар можно получить только после его срабатывания на первой ступени в ЦВД с последующим повторным нагревом до той же температуры в котле, но уже без контакта с водой.То есть в этом процессе пар становится обычным "перегретым" газом, вдалеке от границ зоны конденсации на диаграмме состояния . "Влажны" и "насыщеный" для пара - это синонимы в данном случае
Хотя даже первичный пар можно получить перегретым, если отбирать его из более холодной зоны котла, а потом догревать в горячей зоне котла , но уже внутри трубы с одним только паром (то есть в теплообменнике первичного перегрева).
Теплообменник может находится и в самом котле, это не меняет его конструктивной задачи , а именно: передача теплового потока через твёрдую стенку без прямого контакта двух разных теплоносителей.
Согласен!!!...Сам считаю трубопроводные системы вообще не разбираясь с кинематикой жидкости...А в ВУЗе просто сдал...)))
СОГЛАСЕН!!!...Как раз для студентов и просто интересующихся вопросом я и пишу...Я пишу с позиции: Начни объяснять другим, а за одно и сам поймёшь...)))

Oedo
05.09.2023 16:531.Определимся с терминами. Котёл на ТЭС, это не бочка, дна у него нет. То, о чём вы пишете, это барабан котла, в нём да, частично вода.
Сразу из барабана котла ТЭС перегретого пара быть не может. Для этого пар из барабана для начала направляется в конвективный пароперегреватель. А из агрегата, называемого котёл ТЭЦ, вполне себе перегретый пар выходит и направляется в голову турбины, в ЦВД.
На прямоточных котлах вообще без барабана, и без дна, но суть схемы та же.
Кстати тема не сложная, любой учебник по котлам ТЭС описывает схему доступным языком.
2. Ну и про перегрев пара при срабатывании в турбине на ТЭС, это не верно. Посмотрите T-S диаграмму паросилового цикла, температура пара в турбине только нагло падает (простым языком, внутренняя энергия переводится в механическую) и параметры стремятся в зону влажного пара (а чтобы раньше времени пар не стал влажным придумали промперегрев).

iMonin Автор
05.09.2023 16:53Согласен. Но эта тема не этой статьи.
-
На перегрев после ЦВД отправляют потому, что уже вода начинает конденсироваться из пара, и при дальнейшем срабатывании "мокрого" пара просто зальёт турбину.
После перегрева до + 500С сработанного на ЦВД пара его уже расширяют на ЦСД и ЦНД аж до +40С с давлением 7% атмосферного (то есть разрежение как на высоте выше 20км). Хотя бывают турбины, где есть и третий перегрев перед ЦНД.

Samid777
05.09.2023 16:53+3Зачем бороться так сильно с правилом Бернулли?
Вспомнился мне один случай. Был я ну курсах, в школе выживания. Отправили нас в лес, в не очень сильный мороз. Наша группа из примерно 10 коллег по службе натянула палатки между деревьями, в форме шатра, разожгли костер, сидим, греемся, пьем чай. А через некоторое время поменялся ветер, дым заходит внутрь, и у нас состоялся некоторый диалог.
* Господа, в связи с тем, что дым задувает, я предлагаю переместить щель в верхней части шатра, и разместить ее так, чтобы она находилась с подветренной стороны. Согласно правилу Бернулли, в районе щели дующим ветром будет создаваться разряжение, что приведет к возникновению более сильной тяги, чем созданная за счет естественной конвекции.
******* Дмитрий, мы бы предпочли использовать эмпирический метод в решении данной задачи. Мы не сомневаемся в существовании правила Бернулли, но считаем его не применимым в конкретной ситуации. Мы так же хотели бы избавиться от дыма, но считаем что это можно сделать только другими способами.
* Я уважаю Ваше мнения Господа, но вынужден не согласиться с Вами. Потому прошу, одолжить иголку, и передать в безвозмездное пользование нитку у того, у кого она имеется. Это нисколько не помешает реализацию Вашего метода решения, на который требуется некоторое время, за которое, как я считаю, успею восстановить авторитет великого ученого.
******* Пожалуйста, возьмите все необходимое, дабы мы не сможем убедить Вас, что данный метод не сработает. Но Вы скорее всего это сделаете самостоятельно после неудачной реализации данной идеи.
Беру иголку, нитку, зашиваю щель с одной стороны, делаю с другой. Зашиваю края ткани чтобы щель не закрывалась. О чудо, ветер, перестает задувать дым, устанавливается отличная тяга.
* Господа, говорю я наслаждаясь вкусом черного чая с пеплом, как видите, Бернулли не зря сделал свое открытие. Если желаете, я могу рассказать о нем подробнее.
******* Спасибо, все оказалось действительно просто. Теперь мы даже не сомневаемся в этом. Но обсудить правило Бернулли мы бы предпочли немного в другое время, возможно не в ближайшее.
ВОзможно некоторые слова и обороты речи заменены на синонимы, но основная суть разговора сохранилась.
Так что даже если правило Бернулли не используется в расчетах, это не значит, что оно не работает. Мы к примеру в расчетах электрических цепей не используем перемещение зарядов, хотя могли бы делать и так. Но зачем?
iMonin Автор
05.09.2023 16:53-2ОТЛИЧНЫЙ ПРИМЕР!!!
Вот только устройство ориентированного дефлектора на вершине конуса палатки не объясняется "уравнением Бернулли", но при этом легко объясняется "разрежением под изогнутым потоком". Именно так объясняется действие как ветрового дефлектора, так и естественной тяги в домах при ветре (то есть без тепловой тяги за счёт разницы температур).
Про это я у же писал (читайте по ссылке)
https://habr.com/ru/articles/736140/
Некоторые ещё говорят, что электричество в розетках- это "Магическая сила"...Но это же не повод им верить на слово?...Даже если они в доказательство включат в розетку "магический прибор" со светящимися картинками и живыми человеческими голосами...)))

mayorovp
05.09.2023 16:53А это самое "разрежение под изогнутым потоком" (которое, к слову, вообще не гуглится) чем объясняется?

iMonin Автор
05.09.2023 16:53А как вы думаете, почему оно не гуглится, если в ВУЗах всё объясняют по уравнению Бернулли с идеальной жидкостью?
Вот лекция профессора аэродинамики Кембриджского университета Хольгера Бабинского про то - как и за счёт чего образуется так называемая "подъёмная сила" с опровержениями 2-х общепринятых и неверных объяснений. Он об этом записал видос со своей лекции по Аэродинамике крыла ещё в 2004 году.
https://yandex.ru/video/preview/3102839667883048430
Статью он тогда же ровно на эту тему написал

iMonin Автор
05.09.2023 16:53Кстати в Яндексе на запрос "разрежение под изогнутым потоком" вываливается море ссылок...)))

andi123
05.09.2023 16:53+2Лавры Ацюковского не дают покоя.
Давно заметил, что в "эфиродинамику" и "торсионные поля" ударяются исключительно к.т.н.

iMonin Автор
05.09.2023 16:53-2Вы это уже писали мне несколько раз под другими моими статьями здесь.
В данном случае тут нет вообще ничего сложнее механики на уровне уроков Физики средней школы.

mayorovp
05.09.2023 16:53На уроках физики в средней школе закон Паскаля работает, в отличии от ваших статей.

iMonin Автор
05.09.2023 16:53-2На уроках физики многое дают очень упрощённо, чтобы детское сознание хоть что-то усвоило на сильно упрощённых моделях.
Но это не повод оставаться в таких детских представлениях о реальном мире и после окончания школы...))
Например , упомянутый вами "закон Паскаля" является вовсе не "законом", так как действует не всегда и не везде.
Вот вам цитата из вашей же статьи в Википедии:
В случае движущейся несжимаемой жидкости можно условно говорить о справедливости закона Паскаля, ибо добавление произвольной постоянной величины к давлению не меняет вида уравнения движения жидкости (уравнения Эйлера или, если учитывается действие вязкости, уравнения Навье — Стокса), однако в этом случае термин закон Паскаля, как правило, не применяется.

mayorovp
05.09.2023 16:53В локальном виде закон Паскаля прекрасно применяется. Более того, в тех же уравнениях Эйлера или Навье-Стокса он постулируется самим видом этих уравнений.

konst90
05.09.2023 16:53Например , упомянутый вами "закон Паскаля" является вовсе не "законом", так как действует не всегда и не везде.
Законы Ньютона, знаете ли, тоже не всегда работают. Смещение перигелия Меркурия тому пример. Что никак не мешает применять оные законы на практике, делая в некоторых случаях поправку на ОТО.
Аналогично и с законом Паскаля. Он - про гидростатику, а не про гидродинамику. И применительно к покоящейся либо очень медленно движущейся жидкости (например, в гидравлическом прессе) он работает прекрасно, позволяя с достаточной точностью рассчитывать необходимую площадь поршней и толщину стенок. А вот когда мы считаем насос в том же прессе - да, тут нам закона Паскаля не хватит и придётся использовать Навье-Стокса.

iMonin Автор
05.09.2023 16:53-2Вы совершенно правы, что "закон Паскаля"- это про гидроСТАТИКА!!!
Я же говорю, что в гидродинамике есть нюансы, в которых надо учитывать местные ускорения отдельных элементов потока, которые на поворотах труб и создают центростремительные давления, которые вдоль потока вообще не действуют.
Про не действия глобальных законов в большом Космосе - это вы совершенно правы.
Вот только там не законы Ньютона не действуют, а Гравитация оказывается вовсе не глобальным взаимодействием.
Так наша ближайшая соседка Луна просто игнорирует притяжение Солнца, хотя оно аж в ДВА РАЗА сильнее притягивает Луну, чем Земле притягивает Луну.
Это известный факт, который просто игнорируют все адепты глобальной Гравитации.

mayorovp
05.09.2023 16:53+1Так наша ближайшая соседка Луна просто игнорирует притяжение Солнца, хотя оно аж в ДВА РАЗА сильнее притягивает Луну, чем Земле притягивает Луну.
Лол што?
Если бы Луна игнорировала Солнце, она бы никак не смогла удержаться на Земной орбите. Улетела бы по инерции в течении первого же месяцев...

iMonin Автор
05.09.2023 16:53-1Не понял вашего удивления...))
Именно потому, что Луна игнорирует притяжение Солнца, ей удаётся летать вокруг Земли практически по круговой орбите.
Иначе бы Луна ушла к Солнцу в момент прохода между Землёй и Солнцем. Такое положение Луны случается каждый месяц.
Этот феномен указан даже в Википедии, но это никак не добавляет внимания к вопиющему ПАРАДОКСУ в отношениях реальности к теории.
Но почему-то всех очень интересуют аномалии траекторий далёкого Меркурия...)))

konst90
05.09.2023 16:53Иначе бы Луна ушла к Солнцу
Так она и уходит к Солнцу.
Если изобразить орбиту Луны вокруг Солнца - то будет видно, что это выпуклая кривая. То есть - Луна в момент каждый момент времени "поворачивает" в сторону Солнца. Но, поскольку Земля делает то же самое - под влиянием, как это ни удивительно, притяжения того же Солнца - то расстояние между Землёй и Луной сохраняется плюс-минус тем же.

iMonin Автор
05.09.2023 16:53-1Не натягивайте сову на глобус!
Если бы вы построили схему сил, приложенных к Луне от Земли и Солнца, то вам бы никак не удалось заставить Луну заходить за Землю.
Попробуйте, вам понравиться...)))

mayorovp
05.09.2023 16:53Если бы вы построили схему сил, приложенных к Луне от Земли, но не от Солнца, вам бы никак не удалось удержать её на орбите Земли.

konst90
05.09.2023 16:53Если бы опровергнуть теорию гравитации было бы так просто - вы бы без труда могли бы показать расчёт, в котором это сделано. Но вы этого сделать, разумеется, не сможете.
Вы просто голословно утверждаете, что Луна не может уйти за Землю, хотя очевидно обратное. Возьмём момент времени t=0, в котором Луна притягивается Солнцем и Землёй, а Земля только Солнцем, при этом Луна находится между Солнцем и Землёй и движется относительно Земли параллельно касательной к её орбите быстрее Земли. Что тогда произойдёт?
Правильно, Земля полетит по круговой орбите, а Луна - по некоторой кривой с радиусом меньше орбиты Земли. Что с неизбежностью приведёт к тому, что летящая по прямой Луна будет удаляться от Солнца, а летящая по орбите Земля - оставаться на постоянном расстоянии от него. И в какой-то момент Луна пересечёт орбиту Земли, а потом и уйдёт за неё. После чего Земля и Солнце будут тянуть её в одну сторону - к Солнцу. И Луна опять окажется ближе к Солнцу, чем Земля. И так - постоянно. Что и можно увидеть в модели по ссылке, которую я привёл.

iMonin Автор
05.09.2023 16:53-1Я много раз делал эти расчёты с системой Солнце-Земля- Луна, но не здесь.
Здесь я этим заниматься не буду, тут про гидродинамику и уравнение Бернулли.
Что до последнего абзаца, то вы каким-то образом дали возможность Луне лететь не в сторону большей сил, а против её действия. Как вам это удалось????.
Ведь наибольшая сила для Луны- это притяжение Солнца, и в момент положения между Солнцем и Землёй Луна пойдёт уже по околосолнечной орбите, удаляясь от Земли (с отставанием) в сторону Солнца на более близкую к Солнцу орбиту.

konst90
05.09.2023 16:53Я много раз делал эти расчёты с системой Солнце-Земля- Луна
вы бы без труда могли бы показать расчёт, в котором это сделано. Но вы этого сделать, разумеется, не сможете.
и в момент положения между Солнцем и Землёй Луна пойдёт уже по околосолнечной орбите, удаляясь от Земли в сторону Солнца по более близкой орбите к Солнцу
Вы снова забыли, что Земля тоже притягивается Солнцем. Если обнулить гравитацию Земля-Луна, то они будут первое время двигаться параллельно, не меняя расстояния друг от друга. Но поскольку гравитация между ними не нулевая - Луна будет отклоняться от круговой орбиты. Новая кривая по-прежнему будет иметь центр кривизны со стороны Солнца, но кривизна будет меньшей - и Луна начнёт удаляться от Солнца.

iMonin Автор
05.09.2023 16:53-1Вы в самом деле не способны выстроить вектора сил на одной прямой Солнце -Луна Земля и понять будущее движение Луны, если сила притяжения Луны Солнцем в два раза больше, чем притяжение Землёй Луны?
Для этого ничего считать НЕ НАДО!...Всё уже посчитано!!!
Вывод: в ы просто отказываетесь признать очевидную проблему существования системы планет и звезды, которой в привычной системе Глобальной гравитации существовать не может.
Решением этого парадокса является версия "Гравитационных сфер планет", где в границах определённого радиуса от планеты учитывается только притяжение этой планеты, но не Солнца.
Причём версия "Гравитационных сфер планет" вполне себе ищется в поисковиках

konst90
05.09.2023 16:53.Всё уже посчитано!!!
вы бы без труда могли бы показать расчёт, в котором это сделано. Но вы этого сделать, разумеется, не сможете.
Вы в самом деле не способны выстроить вектора сил на одной прямой Солнце -Луна Земля и понять будущее движение Луны, если сила притяжения Луны Солнцем в два раза больше, чем притяжение Землёй Луны?
Способен. И я уже описал, что произойдёт.
Но я с интересом жду вашей версии. Возьмём момент времени t=0, в котором Луна притягивается Солнцем и Землёй, а Земля только Солнцем, при этом Луна находится между Солнцем и Землёй и движется относительно Земли параллельно касательной к её орбите быстрее Земли. Что тогда произойдёт?

iMonin Автор
05.09.2023 16:53-1Луна движется МЕДЛЕННЕ Земли на 1 км/с по орбите относительно Солнца. (то есть вы даже не в курсе как вращается Луна вокруг Земли и Солнца)
Следовательно Луна будет отставать от Земли, двигаясь в сторону Солнца, так как туда сила в 2 раза больше. С удалением от Земли сила притяжения Луны к Земле будет только падать, а к Солнцу возрастать при приближении к нему.

konst90
05.09.2023 16:53+1Луна движется МЕДЛЕННЕ Земли на 1 км/с по орбите относительно Солнца. (то есть вы даже не в курсе как вращается Луна вокруг Земли и Солнца)
Не в курсе, признаю. Но это не важно, на самом деле. Эффект будет ровно тот же.
Луна будет отставать от Земли, двигаясь в сторону Солнца, так как туда сила в 2 раза больше
А теперь смотрим на цифры. Земля движется по своей орбите (для простоты - круговой) радиусом 1 а.е. со скоростью 30 км/сек. Луна - на расстоянии ~0,998 а.е со скоростью 29 км/с. Оба вектора скорости направлены перпендикулярно направлению на Солнце. Притягиваются Солнцем они, соответственно, практически одинаково, разница по закону обратных квадратов - 0,4%. Нормальное ускорение со стороны Солнца, определяемое силой притяжения (величина ускорения свободного падения для некоторого радиуса), для них различается на эти же 0,4% - у Земли 1х, у Луны 1,004х.
А вот разница скоростей - 3%, то есть квадрат скорости для Земли - 900, для Луны - 841.
Однако у Луны есть ещё и нормальное ускорение со стороны Земли, направленное к Земле (то есть от Солнца). Оно, как вы утверждаете, вдвое меньше солнечного, пусть будет 0,502x. Вернее, -0,502х, поскольку направлено от Солнца. Соответственно, сумма этих ускорений будет равна 0,502x.
Теперь определяем радиус кривизны траектории. Если
, то
. Считаем - и получаем для Земли кривизну 900/1 = 900, для Луны 841/0,502 = 1675.
Мы видим, что радиус кривизны траектории Луны больше, чем у Земли. Мы исходили из того, что орбита Земли круговая, то есть Луна, имея больший радиус кривизны, будет (в момент, когда находится между Солнцем и Землёй) удаляться от Солнца.
Вот и вся математика - это уровень средней школы.
Двигаясь по своей околосолнечной орбите медленнее Земли, Луна отстанет от Земли, и, отдаляясь от Солнца, в какой-то момент пересечёт орбиту Земли. То есть - окажется за Землёй на том же расстоянии от Солнца. В этот момент она будет иметь траекторию той же кривизны, но скорость будет возрастать - ведь Земля тянет её по орбите вперёд. Но, поскольку ранее кривизна была больше - орбита чуть изменилась, и Луна продолжает лететь за Землю, уже догоняя её. Соответственно, улетев за Землю, Луна притягивается в сторону Солнца и Солнцем, и Землёй, в результате чего оказывается ближе к Солнцу, чем Земля. Но, поскольку она летела перед Землёй - та затормозила её, и теперь скорость Луны меньше чем у Земли. И так по кругу.
Возвращаясь к началу - если бы в t=0 Луна, находясь ближе к Солнцу, двигалась бы быстрее - это изменило бы порядок положений, но не суть орбитального движения. Поэтому я и написал, что меня это не интересует: мы бы увидели то же, но в обратной перемотке.
А теперь с интересом жду опровержения в виде ваших расчётов. Расчётов. Хотя предвижу, что вы этого сделать, разумеется, не сможете.

iMonin Автор
05.09.2023 16:53-21.Расчёт в целом правильный.
-
Выводы сделаны неверные, так как ситуация развивается иначе, чем вы представляете себе. Реальность выглядит так:
А) Кривизна траектории будет больше кривизны земной траектории , то есть действительно некоторое время Луна будет стремительно отставать от Земли со скоростью 1 км/с и при этом очень медленно удалятся от Солнца, так как кривизна траектории в 2 раза меньше земной..
Б) Скорость изменения расстояния до Земли и Солнца отличаются в несколько тысяч раз ,если считать в процентах к радиусам. То есть пока Луна отстаёт от Земли, в это время сила притяжения к Земле резко падает и разворачивается в сторону от Солнца. В результате через неделю от парада планет Земля теряет Луну когда она уходит назад на удаление в 1,5*R по околосолнечной орбите и на 2*R (по теореме Пифагора), где сила притяжения к Солнцу возвращается, ибо Земля уже не компенсирует её в направлении к Солнцу, а сама Земля тянет Луну в 4 раза слабее (квадрат от 2*R), то есть сильно слабее тянет к себе, чем нужно для удержании рядом с собой.
ИТОГО.: Луна отстала от Земли и отправится на эллиптическую орбиту вокруг Солнца ниже орбиты Земли
-

mayorovp
05.09.2023 16:53ИТОГО.: Луна отстала от Земли и отправится на эллиптическую орбиту вокруг Солнца ниже орбиты Земли
…и это действительно однажды произойдёт, однако мы с вами до этого момента не доживём.
А вот если "убрать" влияние Солнца на Луну — Луна отстанет от Земли и улетит с её орбиты в течении первых же месяцев.

iMonin Автор
05.09.2023 16:53-2У вас странная логика!
Если сейчас Луна не подчиняется явно большему влиянию притяжения от Солнца, то если его убрать, то Луна и притяжение земли перестанет воспринимать?
Вы уж разберитесь как-то внутри себя: Земля вообще притягивает Луну, или Луна ходит вокруг Земли по привычке, не подчиняясь законам Ньютона?

mayorovp
05.09.2023 16:53+1Луна ходит вокруг Земли в силу законов Ньютона, конечно же. Однако, это работает только для неподвижной Земли (а также для движущейся равномерно и прямолинейно, в силу преобразований Галилея).
Как только Земля начинает улетать под действием притяжения Солнца — Луна больше не может держаться на орбите вокруг Земли (если на Луну каким-то образом перестало действовать Солнце, конечно же).
Проще всего этот эффект показать в системе отсчёта, в которой Земля неподвижна. В этой СО притяжение Солнца уравновешивается центробежной силой инерции, которая так же действует и на все остальные тела (потому что является математическим фокусом, а не реальной силой). В том числе она действует и на Луну. И теперь смотрите фокус: сила инерции, действующая на Луну, тащит её в сторону с силой, в два раза превышающей притяжение Земли! Никакой орбиты вокруг Земли в таких условиях быть не может.
А вот если вернуть в рассмотрение притяжение Луны к Солнцу — то всё становится значительно лучше. Потому что теперь с орбиты Луну пытается "сорвать" не сила инерции, а равнодействующая силы инерции и силы притяжения. Которые для Земли равны в точности по построению, а в её окрестностях — равны примерно.
Иными словами, "сорвать" Луну с орбиты Земли пытается не вся сила притяжения Солнца, а приливная сила. Которая уже слабее притяжения Земли.

konst90
05.09.2023 16:53+1Если сейчас Луна не подчиняется явно большему влиянию притяжения от Солнца
Ещё раз для танкистов. Луна подчиняется влиянию притяжения Солнца. Именно благодаря этому притяжению Луна вокруг Солнца и летает.

konst90
05.09.2023 16:53+1некоторое время Луна будет стремительно отставать от Земли со скоростью 1 км/с
Это "некоторое время" - одно мгновение. Как только Луна хоть на немного отстанет от Земли - вектор притяжения повернется, и появится сила, которая разгоняет Луну по своей орбите.
Чем дольше Луна будет уходить от Солнца - тем больше будет становиться эта сила, потому что синус угла Солнце-Земля-Луна будет расти довольно быстро. Т.е. например через сутки после парада планет Луна отстанет (примерно) на 86 тысяч километров по своей орбите, но при этом от Солнца удалится... Здесь мне пришлось нарисовать две окружности, одна радиусом 150, другая с кривизной в 1675/900 раз больше, т.е. радиусом 280, обеспечив им почти-касание - расстояние всего 0,3. А потом провести из центра малой окружности (Солнце) прямую под углом 1 градус от линии, соединяющей центр и точку почти-касания. И оказалось, что от Солнца Луна удалилась всего на 10 тысяч километров. Отставание 80 тысяч километров, приближение к орбите 10 тысяч (стало 290 тысяч), итого по ново расстояние - 300,83 тысячи километра. Никаких полутора радиусов за неделю, потому что теперь у нас Луну по орбите разгоняет сила, равная синусу угла (80/300), т.е. 26% от земного тяготения, вследствие чего Луна разгоняется с ускорением 4.2e-3 м/с^2, в результате чего к исходу вторых суток наберет 366 м/с, снизив скорость отставания от Земли с 1000 до 634 м/с. К исходу третьих суток синус вырастет ещё больше, и к концу недели мы увидим, что набранная за эту неделю скорость позволит Луне лететь по орбите со скоростью Земли, сохраняя расстояние до неё. Ещё через неделю Луна, догоняя Землю, окажется дальше неё от Солнца, при этом двигаясь быстрее.
Посчитав же следующие две недели, причём с достаточно мелким шагом - придём к моменту поворота всей системы на 28 градусов с сохранением того же относительного положения и скоростей, что и в t=0. Делается это при базовых знаниях любого языка программирования за несколько часов, при продвинутых - ещё и анимацию можно сделать.
Но с этим "посчитать" есть маленький нюанс, на который я уже несколько раз обращал внимание. Если бы опровергнуть теорию гравитации было бы так просто - вы бы без труда могли бы показать расчёт, в котором это сделано. Но вы этого сделать, разумеется, не сможете. Вот просто взять - и посчитать, вручную или программой, и изложить результаты в тексте с формулами и картинками. И ни один сторонник "теории сфер тяготения" не сможет, потому что антинаучные теории с расчётами стыкуются весьма плохо.

iMonin Автор
05.09.2023 16:53-2"Задача трёх тел"- это классическая задача в механике, которая не имеет общего аналитического решения.
Существуют частные решения по типу "квазистатических систем", например "точки Лагранжа"
Система трёх тел "Луна-Земля-Солнце" не является частным решением, и не может быть стабильной в границах условий чисто гравитационных взаимодействий
Итого: Если вы хотите продолжать спорить про достоверность теории чисто гравитационного удержания солнечной системы в стабильном положении, то обратитесь к профессиональным Сенологам, которые десятилетиями пытаются вычислять движения Луны по каким-то странным эмпирическим зависимостям с очень хреновой точностью. То-то мужики обрадуются вашим простеньким решениям этой неразрешимой до сих пор задачи!!!...)))

mayorovp
05.09.2023 16:53+1Извините, а кто вам сказал что Солнечная система находится в стабильном положении? И почему отсутствие аналитического решения вы приравниваете к невозможности сделать предсказание на несколько (тысяч) лет вперёд?
И да, идти радовать селенологов со своими простыми решениями лучше вам, ведь простые "решения"-то именно вы и предлагаете.

iMonin Автор
05.09.2023 16:53Вообще-то статья про Уравнение Бернулли и ограниченность его применения вне обычных твердых труб..
Про космос начал не я, так что и претензии не ко мне...
Нестабильная система разваливается сразу, а не существует тысячи лет подряд во многих десятках тысяч повторённых циклов...
В селенологии все расчёты эмпирические, то есть методом систематической подгонки результатов будущих прогнозов по данным случившихся наблюдений...)))

mayorovp
05.09.2023 16:53Нестабильная система разваливается сразу, а не существует тысячи лет подряд во многих десятках тысяч повторённых циклов...
Между явной стабильностью и явной нестабильностью есть куча промежуточных состояний.
В селенологии все расчёты эмпирические, то есть методом систематической подгонки результатов будущих прогнозов по данным случившихся наблюдений...)))
И, тем не менее, эти случившиеся наблюдения никак не противоречат задаче трёх тел. А вот вашей идее с выборочной гравитацией — противоречат.

konst90
05.09.2023 16:53Если вы хотите продолжать спорить про достоверность теории чисто гравитационного удержания солнечной системы в стабильном положении
Я хочу увидеть хоть какие-то доказательства "известного факта" - "наша ближайшая соседка Луна просто игнорирует притяжение Солнца". Потому что мне из базового курса астрономии известно обратное - Луна вращается вокруг Солнца под воздействием его притяжения.
Но почему-то ни в среде "профессиональных сенологов" (они сено изучают, что ли?), ни в среде профессиональных программистов, ни в среде каких-либо других профессиональных профессионалов нет людей, которые могли бы этот "известный факт" подтвердить расчётами. По странному совпадению, нет таких людей и среди сторонников альтернативных теорий - но, подозреваю, потому что они считать не умеют. Во всяком случае, я таковых расчётов не видел.
Мой же тезис остаётся верным:
Если бы опровергнуть теорию гравитации было бы так просто - вы бы без труда могли бы показать расчёт, в котором это сделано. Но вы этого сделать, разумеется, не сможете.

iMonin Автор
05.09.2023 16:53-3Вы даже умудрились запомнить, что я являюсь "кандидатом технических наук", хотя в последних статьях об этом я уже не сообщаю...)))

Daddy_Cool
05.09.2023 16:53+1ктн ктну рознь ). Ну а чего - человек занимался всю жизнь какой-нибудь прочностью или литьем, потом понял, что надо что-то делать великое, ну и... пытается это великое сделать.
Я очень люблю бывать на фрико-докладах - это прям труъ научная фантастика.
Ну кстати справедливости ради, в ведущих институтах РАН ктны обычно нормальные - это обычно экспериментаторы которые хорошо чувствуют непроверяемую лажу или плохие эксперименты, а вот кфмны... куча откровенно завиральных идей в обоснование которых используется математика существенно серьезнее школьный. Другой вопрос, что эти (пусть завиральные идеи) будут трудны для восприятия слабообразованным народом.
Из забавного. У меня знакомая (гуманитарий), как-то позвонила и попросила совета - у неё муж (хороший и интересный человек, по образованию сварщик) собирал дома вечный двигатель - ну там магниты, катушки, и т.п...по советам из интернетов. Ну и просил деньги на это из семейного бюджета. Вот тут же всё просто и понятно - магнит туда, магнит сюда... и вечный двигатель, магниты это ж настоящая магия.
---
А "торсионные поля" - как эффект закрутки пространства (по аналогии с гравитацией) вполне физичны, другой вопрос, что э... слабоваты маленько.
ru.wikipedia.org/wiki/Торсионные_поля
andi123
05.09.2023 16:53+1Понятно, что большинство к.т.н. отличные инженеры и приносят кучу конкретной пользы (в отличии "завиральных" кфмн и дфмн).
Но для великого нужна фундаментальная физика и математика, с которой у них в силу образования, мягко говоря, слабовато. Вот и случается конфузия.

tmxx
05.09.2023 16:53Турбодетандеры используют в газовой промышлености для перевода газа из транспортных магистралей высокого давления 12 атм (от месторождения до района потребления) к распределительным магистралям низкого давления 0,05атм (до конечного потребителя).
То есть давление в газовых трубах может снижаться в 240 раз!
Уважаемый автор, правильно ли я понимаю, что имеется ввиду избыточное давление в магистрали?

iMonin Автор
05.09.2023 16:53Да, вы правы, Я ошибся с цифрой 240 раз.
Абсолютное давление уменьшится всего в 13 раз...
Базовую 1 атмосферу к газопроводу я забыл прибавить.
Так что спасибо за замечание- правку в текст статьи внёс.

gematit
05.09.2023 16:53+1Уважаемый Автор, вы транслируете невероятный бред.
Вы как-то очень тяжело относитесь к интегралу Бернулли (актуальному для стационарного течения идеальной несжимаемой жидкости вдоль линий тока).
Позволю дать Вам несколько усложнённое уравнение для НЕстационарного движения (оно несколько менее популярно, поскольку не входит в школьную физику). Такая штука называется интегралом Коши-Лагранжа. Я понимаю, насколько Вас волнует проблема отсылок к Авторитетам, так что давайте назовём это просто Ещё Одной Формулой.
Предлагаю Вам опровергать это, что куда интереснее опровержения несчастного интеграла Бернулли.
Мне очень лень в Латех, так что прошу проявить понимание.
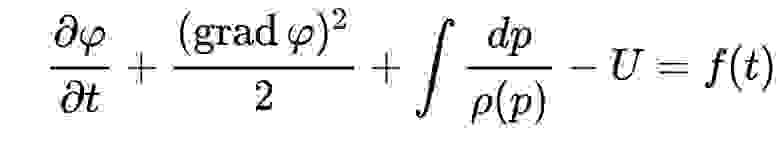
За дальнейшими подробностями пожалуйте в базовые учебники МСС/гидродинамики или хотя бы в Вики.
Хотя о чём я… Вас же там явно забанили.

iMonin Автор
05.09.2023 16:53-2Ваше предложение очень интересное, НО где в интеграле Коши-Лагранжа присутствует центростремительное ускорение при изгибании потока?
Всё это уравнение про перемещение потока вверх и вниз в поле гравитации, но ни разу не про реакцию потока на твёрдую стенку внутри потока жидкости.
У меня нет претензий к Уравнению Бернулли, просто зона его применение очень узкая- для потоков воды в реальных жёстких трубах ( то.есть для практических инженерных расчётов трубопроводных сетей с потерями на местные и линейные сопротивления).
В тоже время УБ пихают всюду (в авиацию и в судовождение) как главное объяснение всех процессов, но при этом оно там ничего не объясняет.

gematit
05.09.2023 16:53+1УБ ничего не объясняет. Оно выводится из уравнений Эйлера для конкретных условий. И применимо именно в этих условиях.
По УБ невозможно рассчитать, как будет выглядеть линия тока. Его можно применять только если известна эта линия тока, а течение является установившимся (в несжимаемой идеальной жидкости).
Важно отметить, что во многих приложениях все условия для УБ вполне выполняются, хотя бы приближённо. Поэтому его и используют.

gematit
05.09.2023 16:53А вообще, Вам бы стоило более полно разобраться с моделью идеальной жидкости.
Ну рано Вам вникать во все эти вязкости, тензоры деформации и прочее.
Но это лишь дружеский совет.

CBET_TbMbI
05.09.2023 16:53+1Автор. Иногда, если слишком умничать - можно показать всем, что... наоборот, в общем.
Это всё не противоречия, а допущения! Может, ещё скажешь, что в законах кинематики есть противоречия. Ведь там тоже не учитываются многие факторы. И подброшенные тела (о, ужас) падают не по параболе, как им следует, а по более хитрым траекториям.
Что касается твоих парадоксов.
Чем первый от второго отличается я не понял. Но! Преобразование скоростного напора в гидростатический происходит на практике. Сам по себе. Открой кран над пустой ванной и увидишь. Если лень, посмотри тут https://youtu.be/4U-J9dzXpgU?si=tLTZUrT53AGecgxX&t=1056 (с 17:30). В начале вода имеет много кинетической энергии, потом она переходит в потенциальную.В чём третий парадокс вообще не понял. Идеальная жидкость не имеет трения. Ну, да. И что? Такой ещё приняли для упрощения. В чём парадокс-то? И как это связано с тем, что её невозможно затормозить?
Четвёртый парадокс ничем не лучше третьего.
И далее ты смело всех посылаешь в лабораторию. Лаборатория, конечно, хорошо, и часто она на самом деле необходима, но не всем она по карману. Почему не рассматриваешь более полные математический модели?
Уравнения Бернулли недостаточно? Используй гидравлические расчёты с учётом потерь. В любом учебнике или справочнике по гидравлике они есть. Если мало и этого, моделируй с помощью Навье-Стокса.
iMonin Автор
05.09.2023 16:53-2Вы уверены, что читали мою статью?
Уравнение Бернулли изначально имело в себе учёт потерь, а потому вполне адекватно описывало реальные трубопроводы.
Использование ИЖ в УБ вместо решения каких-то дополнительных задач только породило кучу неувязок с реальностью, которые я и называл "парадоксами"
На практике НЕ происходит полного преобразования кинетической энергии струи жидкости в статический напор при расширении трубы. Есть только частичное преобразование с большими потерями.
В лабораторию я никого не посылал, так как результаты простого лабораторного опыта я уже представил в статье.
Что вы преплетаете тут Навье-Стокса лишь означает, что сами вы в обсуждаемом предмете не разобрались, но при этом на вас магически действуют нагромождения формул, не дающих никакого вразумительного ответа для реальных задач.

Daddy_Cool
05.09.2023 16:53Не смог удержаться )

Справочники, Навье-Стокс... это всё скучно
и не принесет славы.




abcdsash
в общем все нормально, только ТеХ/LaTeX надо знать для формул на ресурсе
иначе все это смотрится ужасно, то скриншот с одними формулами, то с другими по стилю... да еще и с текстом