Вместо введения

В идеальном мире мы точно знаем, в какой момент времени пользователю нужно напомнить о нашем продукте. Причём таким образом, чтобы он не отказался от наших услуг, а совершил бы новый платёж. Если мы будем излишне активными, отправляя всем нашим клиентам сообщения, то это может стать и раздражающим фактором, и оказаться недешёвым вариантом. Подходы, основанные на анализе вероятности оттока каждого клиента в отдельности — это, безусловно, отличные варианты, но они требуют времени и ресурсов на исследование и разработку.

А что делать, если прямо сейчас у вас нет ни времени на разработку сложных подходов, ни приблизительного понимания, как долго живёт ваш среднестатистический клиент, а задача от бизнеса дать какие-то рекомендации есть?

Меня зовут Артём, я антифрод-аналитик в Каруне, и в данной статье мы рассмотрим достаточно простой подход, с помощью которого можно решить обозначенную проблему. Если вы скажете, что антифрод решает абсолютно другой спектр задач, то будете абсолютно правы. Однако во время работы с одним из проектов при переосмыслении использованного алгоритмического стека в нём, мы пришли к выводу, что отдельные небольшие кусочки этого стека вполне могут подходить и для решения других задач. На базе нашего опыта расскажу, как с помощью байесовского моделирования и библиотеки PyMC3 можно получить примерную картину того, как долго ваш клиент должен быть неактивным, чтобы считать его отточником. Это может помочь ответить на базовые вопросы бизнеса и подготовиться к реализации более точных и качественных моделей (если это потребуется).

Что будем анализировать?

Реальных данных здесь, по понятным причинам, не будет. Но так как статья предполагает возможность практического применения, то мы что-нибудь сгенерируем. Для начала давайте предположим, что мы работаем в аналитике какого-то онлайн-сервиса, который предполагает различные покупки. Специфика сервиса здесь абсолютно не важна. Но для реалистичности предположим, что наш сервис генерирует музыку по текстовому описанию за некоторую стоимость. А самая важная информация о клиентах, которая нам здесь потребуется, это исторические данные о том, как часто они этот сервис использовали за всё его время существования.

Из этой информации мы можем создать две метрики, на которых будет строиться всё дальнейшее исследование:

1. Текущий период неактивности — сколько дней прошло с последнего активного действия клиента по текущий момент.

2. Максимальный период неактивности — наибольшее количество дней между двумя активными событиями клиента без учёта текущего периода неактивности.

А что такое активный клиентский день? По сути — это день, когда клиент совершил какое-то целевое действие. Например, совершил платёж на вашем сервисе, оформил подписку, просто залогинился, какая-то комбинация из различных событий, или что-нибудь другое, что вы сами определите важным.

Рассмотрим схему, чтобы разобраться более подробно:

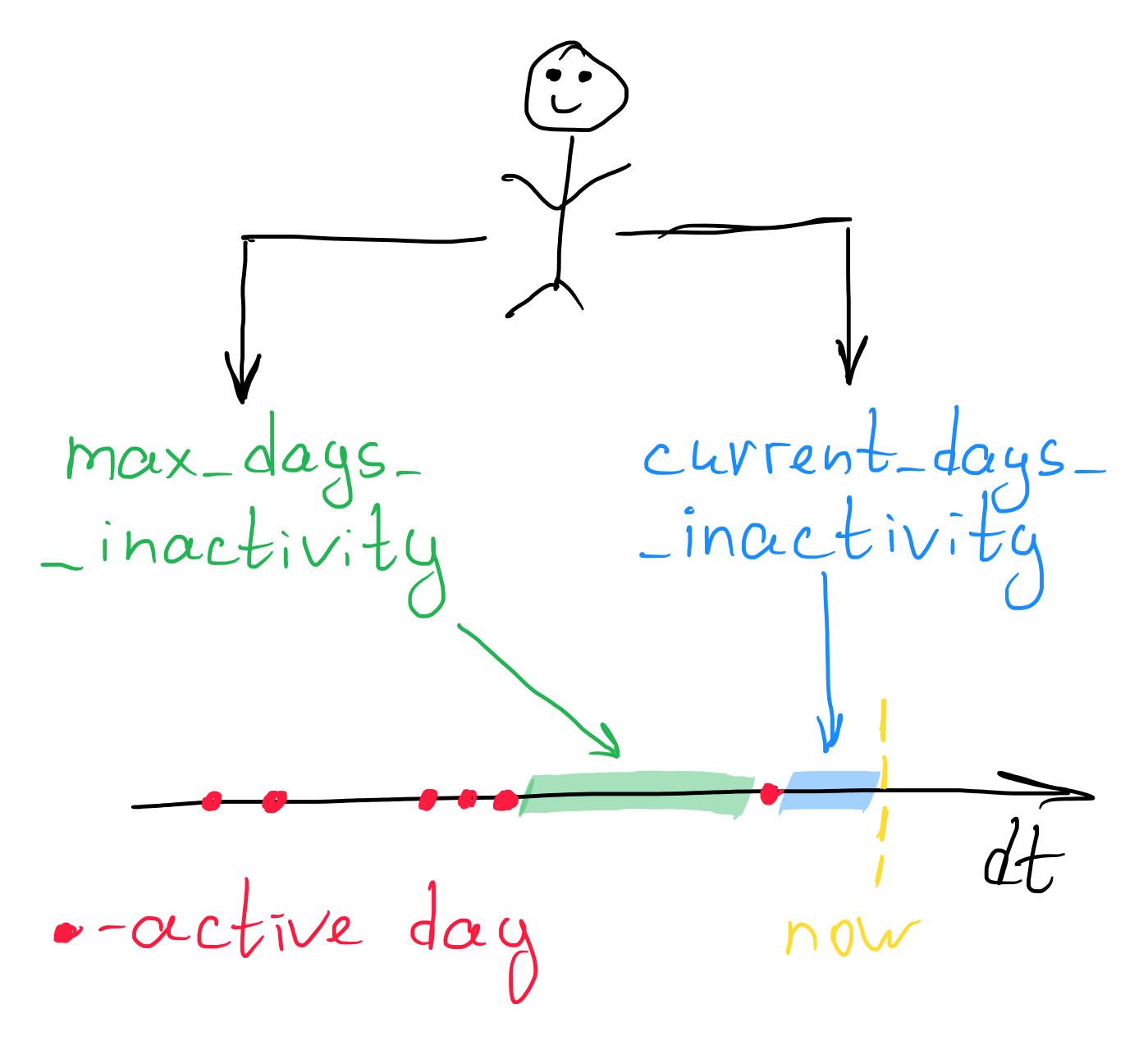
Это наш конкретный клиент. Наша ось, названная dt, представляет временную шкалу. Красными точками на ней отмечены активные пользовательские дни. Жёлтый пунктир — это текущий момент времени. В рамках каждого клиента мы извлекаем текущее количество дней клиентской неактивности. На таймфрейме это синяя область, тут всё просто. Зелёная область — это максимальное количество дней неактивности у того же самого клиента, но с важной оговоркой: текущий период неактивности при расчёте данной метрики мы не рассматриваем. То есть если у кого-то зелёная область составляла бы 20 дней, а синяя — 30 дней, то мы всё равно бы сказали, что максимальное количество дней неактивности составляет 20 дней.

О предположениях и допущениях

Чтобы двинуться дальше, нам нужно принять очень важное предположение: если у клиента метрика количества текущих неактивных дней превышает метрику максимальных неактивных дней, то мы считаем такого клиента отточником. 

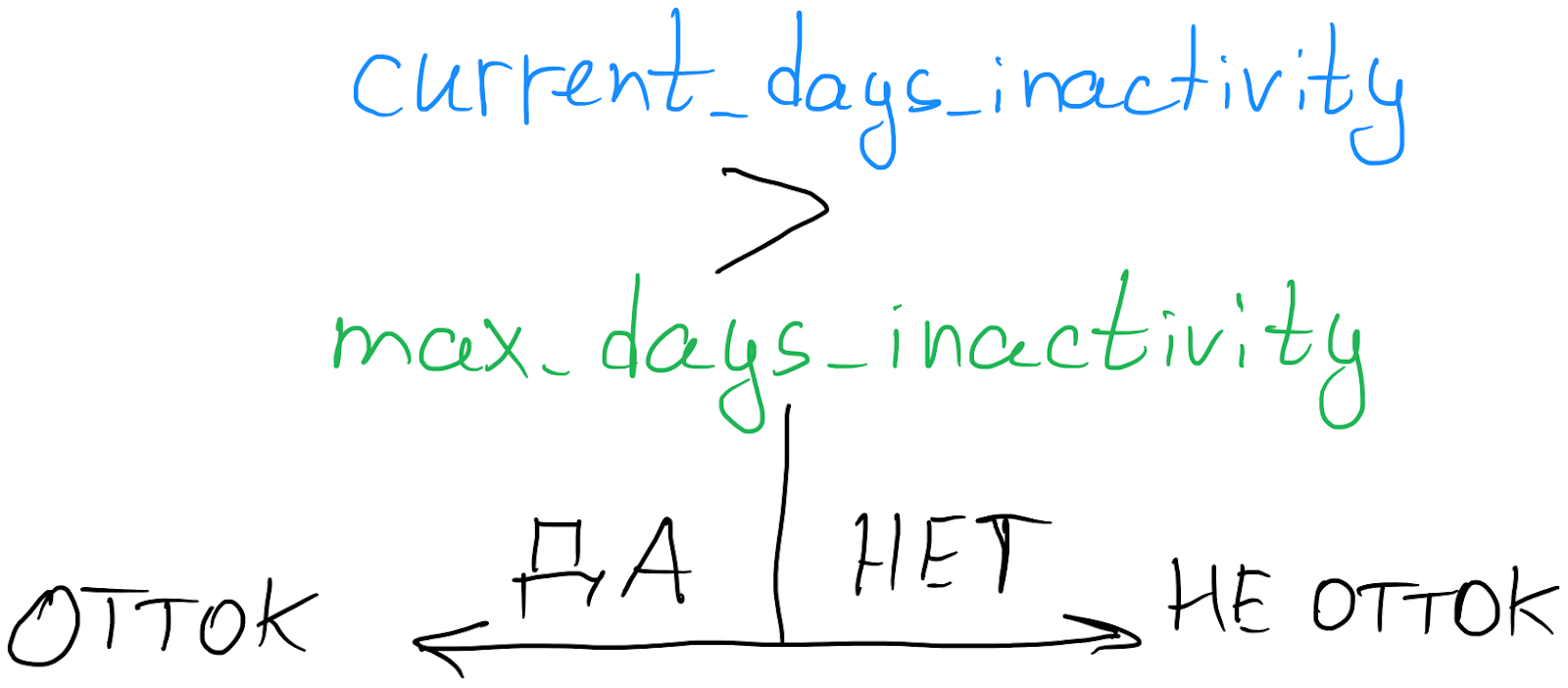
Логика здесь следующая: если к текущему моменту времени какой-то клиент, например, не логинился в нашем сервисе на протяжении 20 дней, но при этом мы знаем, что в истории у него уже бывали и бОльшие периоды простоя, то с определённой долей вероятности мы можем считать, что подобное поведение является типичным для данного клиента.

Соответственно наш анализируемый датасет должен принять примерно такой вид:

Обратите внимание на первые 2 строки в нашем гипотетическом наборе данных, к текущему моменту времени клиенты 111 и 112 имеют по 20 текущих неактивных дней. Но первого мы можем считать отточником, исходя из логики выше, а второго нет. Чем большим количеством данных вы обладаете, тем менее будете подвержены случайным выбросам.

Предлагаемый здесь подход определения оттока — это не истина в последней инстанции. Возможно, у вас на этот счёт могут быть другие идеи. Хочу лишь посоветовать по возможности не пренебрегать выделением различных срезов. Например, отдельно исследовать клиентов по типу используемого устройства или операционной системы, по типу приобретённой подписки, по стране регистрации, и т. д. Как правило, всё это разные выборки, где каждая имеет свои уникальные особенности. Более того, порой можно найти очень неожиданные интересности. Например, вы можете прийти к выводу, что среднее время жизни клиентов, которые пользуются вашим продуктом с ios-устройств, несколько отличается от времени жизни клиентов, предпочитающих android, что абсолютно нормально. Но что если вы обнаружите, что лайфтайм отличается очень сильно? Иногда таким способом можно найти досадные баги, которые и являются причиной негативного опыта пользователей, сокращающих их лайфтайм.

А теперь немного поговорим о допущениях относительно наших пользователей. Иногда их может помочь сформулировать бизнес, но даже если в вашем случае это невозможно, то можно попробовать подойти к вопросу логически.

Как вариант, если ваш сервис предполагает маленькие, но частые покупки, а один из способов привлечения траффика — это оплата за совершение каких-то целевых действий пользователями, например, за оформление подписки или за первое внесение денег на счёт, или что-то в этом роде, то в таком случае может появиться целая прослойка клиентов, заинтересованных лишь в том, чтобы это целевое действие совершить и уйти. А всё потому, что подобные каналы привлечения траффика могли предложить этим клиентам большее вознаграждение, чем они потратят на вашем сервисе за целевое действие. 

Зачем? Потому что ваш бизнес в надежде получить новую платёжеспособную аудиторию может платить ещё больше таким каналам привлечения траффика. По итогу могут получится не очень честные схемы, из-за которых вы получаете не ту целевую аудиторию, на которую рассчитывали. И отдаёте больше денег подобным каналам привлечения, а получаете со всех клиентов сильно меньше

Проблема таких клиентов заключается в том, что их лайфтайм может не превышать 1-2 дней. К тому же таких клиентов может быть немало, и тем самым они будут вносить смещение в вашу выборку.

В данном случае можно просто исключать из рассмотрения всех тех, у кого активное время пребывания на вашей платформе не удовлетворяет какому-то логически обоснованному условию, например, 1 день.

С другой стороны, вам может быть неинтересно рассматривать тех клиентов, у которых количество активных дней уже вроде бы и превышает какой-то адекватный порог, после которого мы можем сказать, что это всё-таки нормальный трафик, но при этом сам клиент совершил ещё слишком мало активностей на сервисе, что тоже не позволяет сказать нам, что он точно заинтересован в нашем продукте. Возможно, он ещё пару раз потыкается на сайте и решит, что мы ему не очень-то и подходим.

Ещё вы можете быть не заинтересованными в рассмотрении тех клиентов, у которых максимальное количество дней неактивности не превышает какого-то порога. Скажем, если у кого-то эта метрика составляет 7 дней, то, может быть, такой клиент просто ушёл в отпуск, и не стоит беспокоиться?

Чем лучше вы знаете специфику бизнеса, в котором работаете, тем большее количество допущений сможете сгенерировать, тут всё достаточно логично.

Приступим к анализу

Так как ранее мы обсуждали, что данные будем генерировать, то давайте так и поступим. Конкретно в этом кейсе я решил, что наша гипотетическая платформа обладает историей почти о 400 пользователей. Обе целевые метрики — текущее и максимальное количество дней неактивности — мы генерируем из дискретного равномерного распределения с диапазоном от 0 до 120 дней. А в качестве допущений я решил, что мне не очень интересно рассматривать всех тех, у кого максимальное количество дней неактивности не превышает 9 дней. Просто кажется, что это не такой крупный срок, после которого стоит бить тревогу.

Начнём с импорта всех необходимых библиотек:

import pandas as pd
import numpy as np
from scipy.stats.mstats import mquantiles
import matplotlib.pyplot as plt
%matplotlib inline

import pymc3 as pm
import theano.tensor as tt
import seaborn as sns

from IPython.display import Image

А также для полной воспроизводимости результатов зададим константы для количества клиентов и фиксации рандома:

NUMBER_OF_CLIENTS = 389
RANDOM_STATE = 100

А ещё не забудем определить функцию, с помощью которой будем навешивать метки оттока нашим гипотетическим клиентам:

def churn_func(max_days_inactivity, current_days_inactivity):
    return 0 if current_days_inactivity < max_days_inactivity else 1

Ну и теперь сгенерируем данные для датасета, который будет анализировать:

np.random.seed(RANDOM_STATE)

max_days_inactivity = np.random.randint(0, 120, size=NUMBER_OF_CLIENTS)
current_days_inactivity = np.random.randint(0, 120, size=NUMBER_OF_CLIENTS)

data = pd.DataFrame({'max_days_inactivity': max_days_inactivity,
                     'current_days_inactivity': current_days_inactivity})

Помните про допущения, о которых мы говорили выше? Их тоже нужно не забыть применить, чтобы оставить только тех клиентов, которые наиболее интересны для нашего анализа:

data = data[data['max_days_inactivity']>10]

data['churned'] = data.apply(lambda x: churn_func(x['max_days_inactivity'], 
                                                  x['current_days_inactivity']),
                                                  axis=1)                                                                
data['churned'].value_counts()

Отлично, данные мы получили. Давайте начнём с того, что визуально оценим, отличаются ли как-нибудь те клиенты, которые, скорее всего, отказались от услуг нашего сервиса, от тех, кто ещё этого не сделал в зависимости от текущего количества дней клиентской неактивности:

plt.figure(figsize=(20, 5))
plt.title('Distribution of customers by churn status')
sns.scatterplot(data, x='current_days_inactivity', y='churned')

Кажется, что поведение пользователей выглядит таким образом, что чем большее количество дней они не пользуются нашим сервисом, тем выше вероятность того, что они отвалились, и их нужно реактививровать. Скорее всего, в своих реальных данных вы увидите похожую картину.

Если подробнее посмотреть на график, то видно, что между гипотетическим оттоком и не оттоком посередине имеется большая площадь перекрытия. И если в минимальных значениях переменной current_days_inactivity  мы можем сказать, что вероятность оттока стремится к нулю, в высоких — к единице, то что происходит посередине — непонятно. Например, мне кажется, что в нашем кейсе вероятность оттока превышает порог в 0.5 где-то между 60 и 80 днями. Но я в этом не уверен.

Чтобы ответить на вопрос, какова же вероятность оттока наших клиентов в зависимости от различного количества текущих дней неактивности, нужно подобрать такую функциональную зависимость, которая начиналась бы где-то в координатах (0; 0) и заканчивалась бы где-то в области (120; 1). Можно, конечно, попробовать подбирать прямую, но интуитивно кажется, что сигмоида здесь оказывается более правильным вариантом.

В общем виде сигмоида задаётся следующим уравнением:

И выглядит график функций следующим образом:

x = np.linspace(-4, 4)

plt.figure(figsize=(7, 5))
plt.plot(x, 1/(1+np.e**(-x)))
plt.axvline(0, linestyle='dashed', color='black', marker='^')
plt.xlabel('x')
plt.ylabel('y');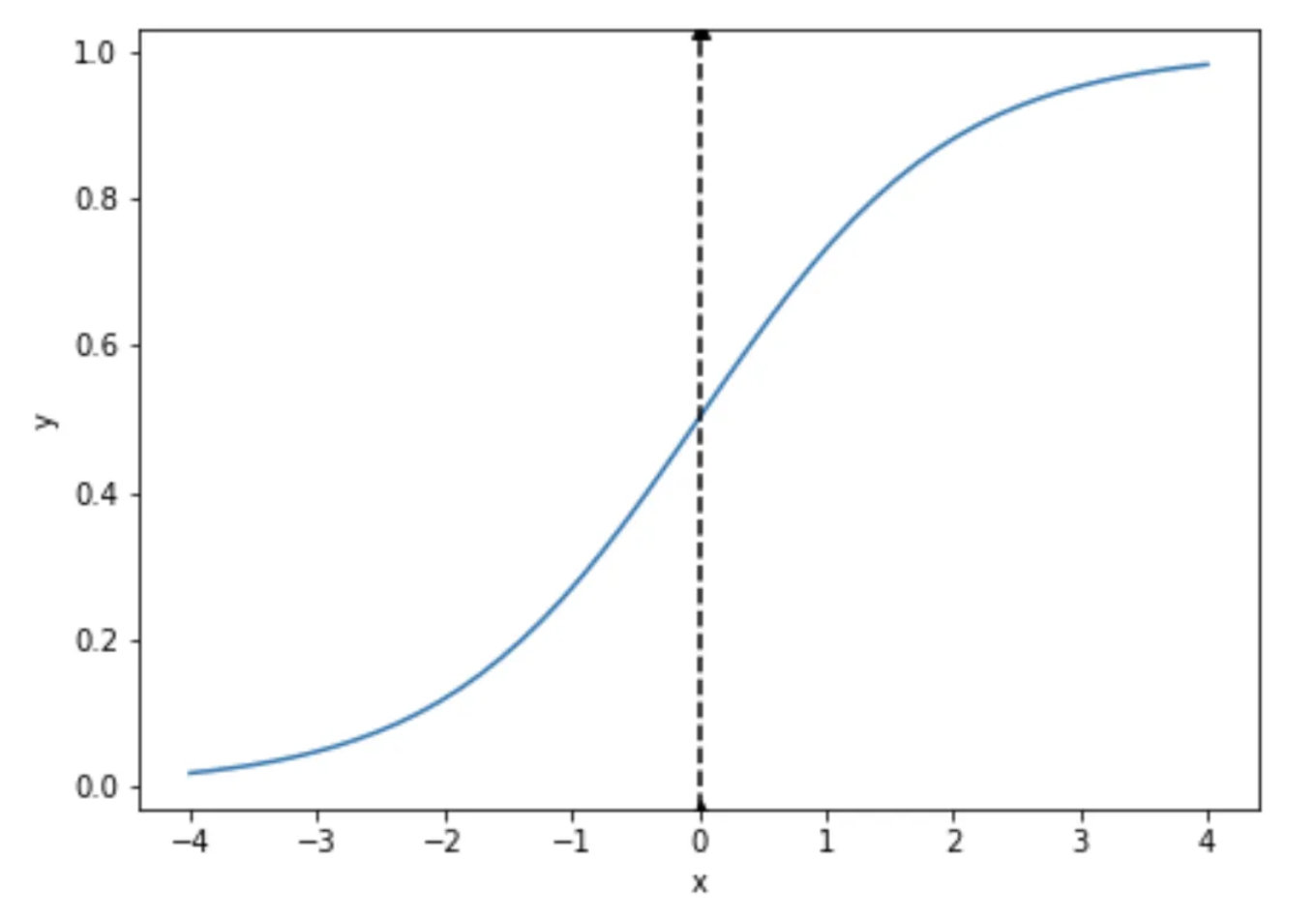

Формула в общем виде для нашего анализа не очень подходит. Во-первых, количество дней текущей неактивности не может быть отрицательным, а во-вторых, вероятность оттока должна пересекать порог в 0.5 где-то после 50 дней или даже больше конкретно в нашем кейса. Но все эти нюансы решаются добавлением всего двух параметров в базовое уравнение:

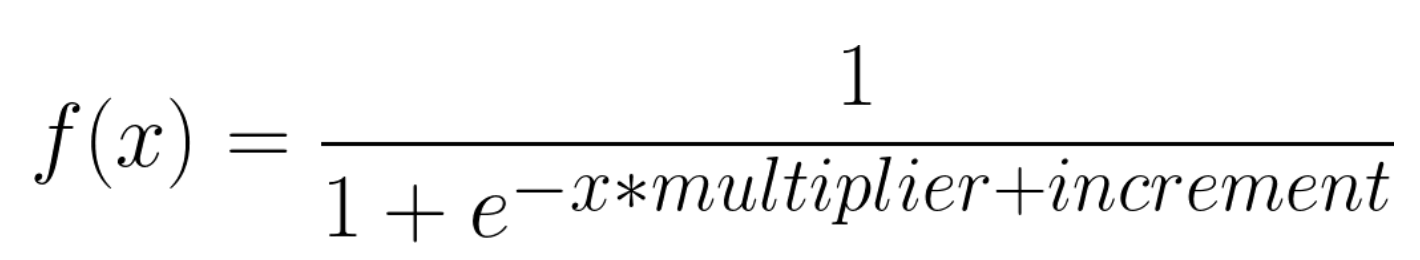
x = np.linspace(-4, 4)

plt.figure(figsize=(7, 5))
plt.plot(x, 1/(1+np.e**(-x*2+3)), label='multiplier=2, increment=3')
plt.plot(x, 1/(1+np.e**(-x*(-5)-2)), label='multiplier=-5, increment=-2')
plt.axvline(0, linestyle='dashed', color='black', marker='^')
plt.legend()
plt.xlabel('x')
plt.ylabel('y');

Давайте подробнее поговорим, за что отвечают добавленные параметры multiplier и increment. С помощью первого мы регулируем крутизну изгиба сигмоиды, а с помощью второго — сдвиг по оси X, ничего сложного.

Таким образом, в данном исследовании нам нужно подобрать такие параметры increment и multiplier, чтобы полученная в итоге сигмоида наилучшим образом описывала наши данные. Для этой цели мы воспользуемся библиотекой PyMC3.

PyMC3 — это библиотека для байесовского моделирования. Если кратко, то в отличие от частотного подхода, в котором искомый параметр должен иметь строго определённое значение, в байесовском мы делаем предположение, что искомые нами параметры находятся внутри какой-то области, которая может покрываться каким-то известным распределением (априорное распределение, наши предположения относительно неизвестного параметра).

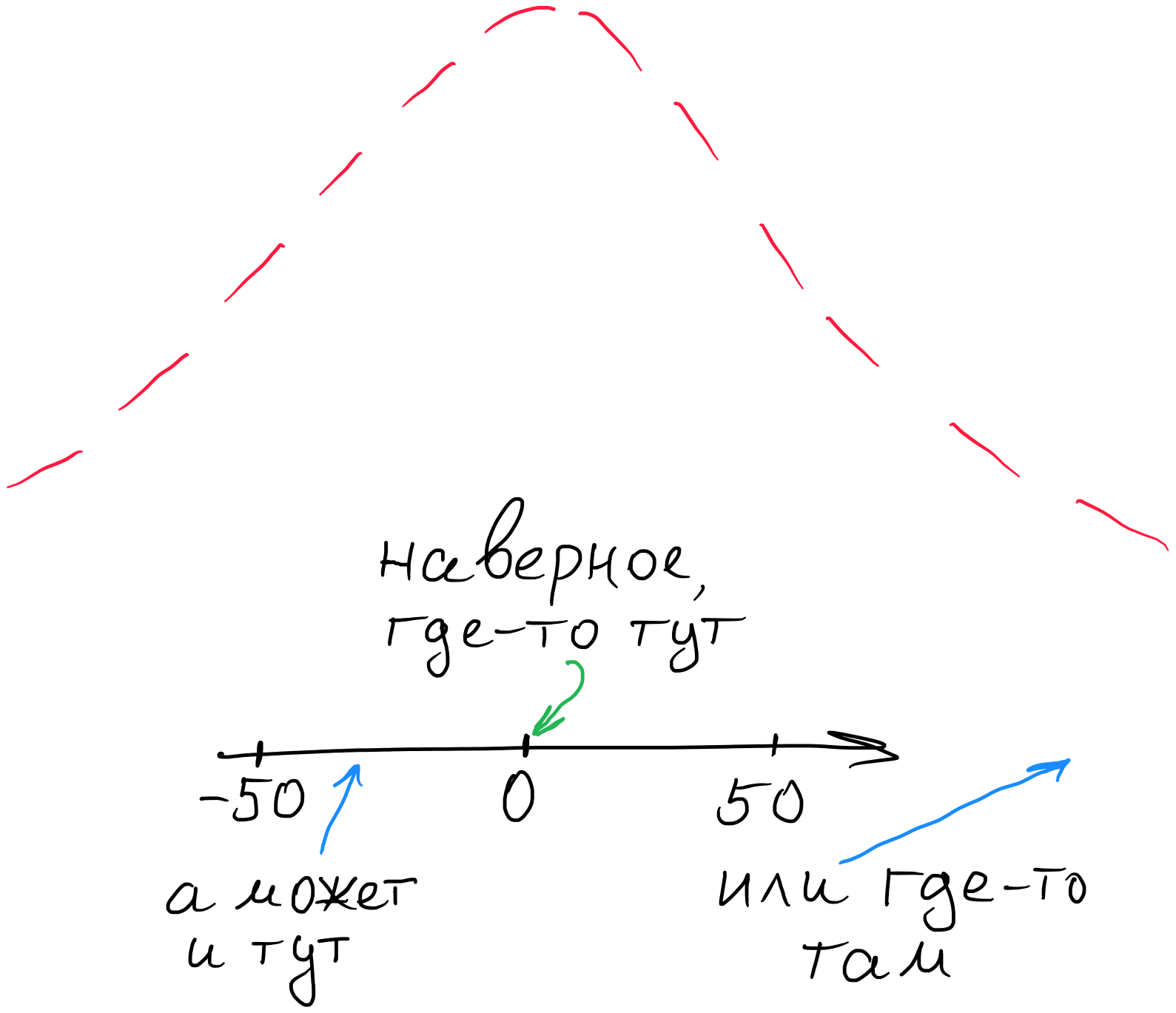
Например, если вы уверены, что какая-то случайная величина распределена непрерывно около какого-то значения, вы можете сделать предположение, что она должна покрываться нормальным распределением, которое покрывает то самое неизвестное значение примерно таким образом:

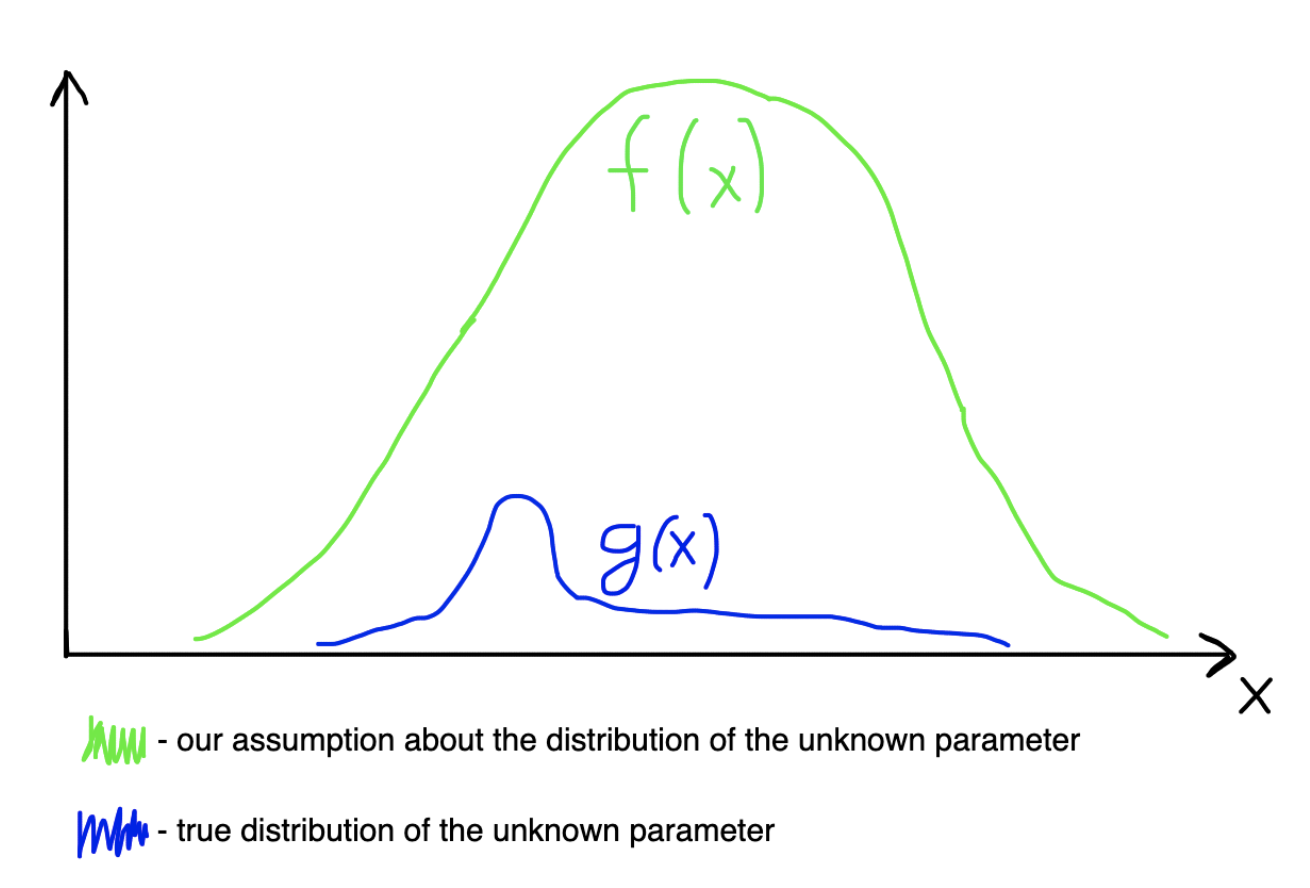
Нам же нужно найти апостериорное распределение, которое вычисляется по следующей формуле:

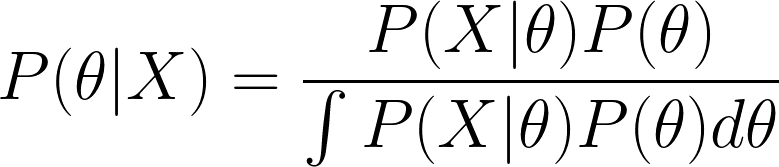
где P(X|????) — правдоподобие, P(????) — априорное распределение.

Апостериорное распределение — это что-то вроде того, насколько мы уверены относительно искомого параметра с учётом имеющихся данных. Формульно это выглядит несколько пугающе, но высчитывать вручную нам ничего не нужно, как раз для этого мы и будем использовать PyMC3. Всё, что нам потребуется сделать — просто подобрать подходящие априорные распределения и подсунуть имеющиеся данные.

Тут стоит сделать важное замечание. Если ваше априорное распределение не будет покрывать неизвестный параметр, как на изображении ниже, то алгоритм не сойдётся.

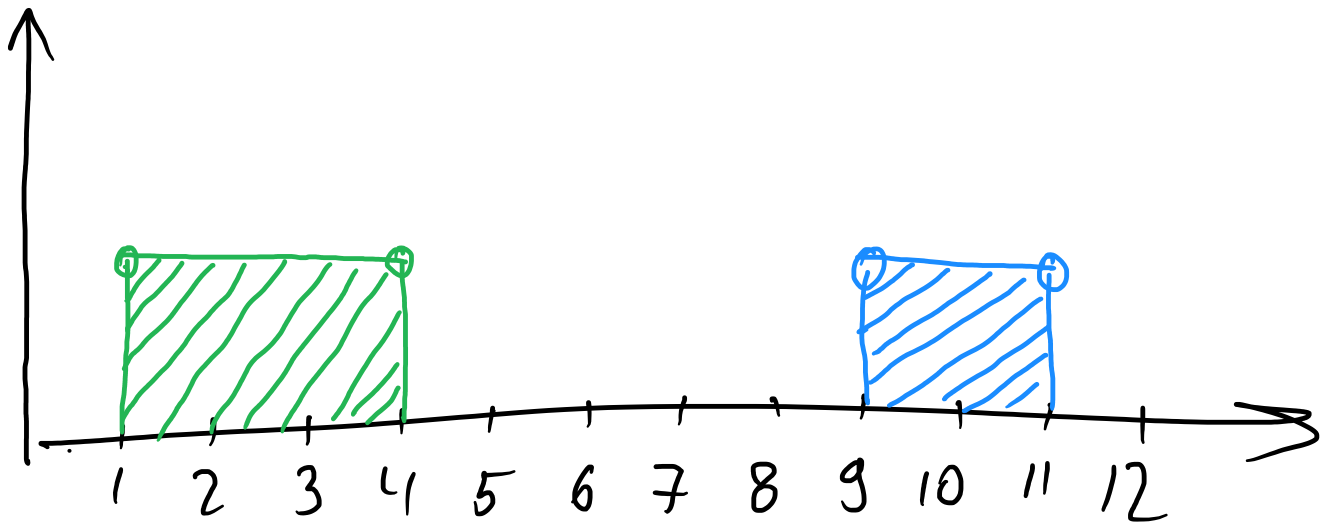
На этом изображении синяя область — это область, где на самом деле находится некий искомый параметр. Зелёная область — это наше априорное распределение, в данном случае — дискретное равномерное. Как видим, оно абсолютно не покрывает синюю область, из-за чего марковская цепь будет осуществлять поиск совсем не там, где должна. Поэтому, если вы сильно не уверены относительно того, где же находится ваш неизвестный параметр, то выбирайте границы распределений побольше, но сильно переусердствовать с этим тоже не стоит, иначе процесс вычисления станет сильно неэффективным.

А что мы можем сказать относительно наших неизвестных параметров multiplier и increment, какие априорные распределения мы можем подобрать для них? Лично у меня нет какого-либо понимания, где они могут находиться. Знаю лишь то, что покрываться они должны непрерывными распределениями. То есть наше априорное предположение относительно искомых параметров следующее: “наверное, это где-то около нуля, но я не сильно в этом уверен=)”. Поэтому я начал бы с нормальных распределений с математическим ожиданием 0, и достаточно большой дисперсией, скажем, 100.

Давайте теперь перенесём всё это в контекст PyMC:

with pm.Model() as model:
    increment = pm.Normal('increment', mu=0, tau=0.01)
    multiplier = pm.Normal('multiplier', mu=0, tau=0.01)
    probability = pm.Deterministic('p', 1/(1+tt.exp(-multiplier*data[
        'current_days_inactivity'] + increment)))
    observed = pm.Bernoulli('observed', probability, observed=data['churned'])
    
    step = pm.Metropolis()
    trace = pm.sample(60000, step=step, random_seed=RANDOM_STATE)

Подробнее остановимся на каждой строке кода. 

В самом начале мы определяем контекстный менеджер, внутри которого будет происходить моделирование. Сразу следом мы задаём априорные распределения для искомых параметров increment и multiplier, параметр tau — это то же самое, что и единица, делённая на стандартное отклонение. Далее мы просто инициализируем детерминистическую переменную probability, в которой задаём уравнение сигмоиды, и передаём её в бернулиевский процесс, в который прокидываем анализируемые данные. Бернулиевский потому, что в наших данных возможно всего 2 исхода: клиент либо отточник, либо не отточник. Если бы исходов было бы больше, нам стоило бы поискать какое-нибудь другое дискретное распределение. А в самом конце мы просто определяем один из семплеров MCMC и желаемое количество извлекаемых семплов.

Практический совет. Если вы обладаете большим количеством данных, скажем, у вас есть десятки или сотни тысяч клиентов, то прокидывание всего этого набора может оказаться не самой хорошей идеей. У вас может либо не хватить оперативной памяти, либо вам придётся очень долго ждать, пока алгоритм не закончит свою работу. Поэтому извлеките выборку из генеральной совокупности, например, с помощью pandas.sample. Оцените визуально, на сколько она соотносится с полным набором данных, и дальше работайте именно с выборкой.

На основании наших предположений относительно искомых параметров, а также имеющихся данных получаем следующие распределения для increment и multiplier:

plt.figure(figsize=(20, 10))
plt.subplot(211)
plt.hist(trace['increment'][:30000], bins=100, density=True, 
         label='posterior of increment')
plt.legend()

plt.subplot(212)
plt.hist(trace['multiplier'][:30000], bins=100, density=True, 
         label='posterior for multiplier')
plt.legend()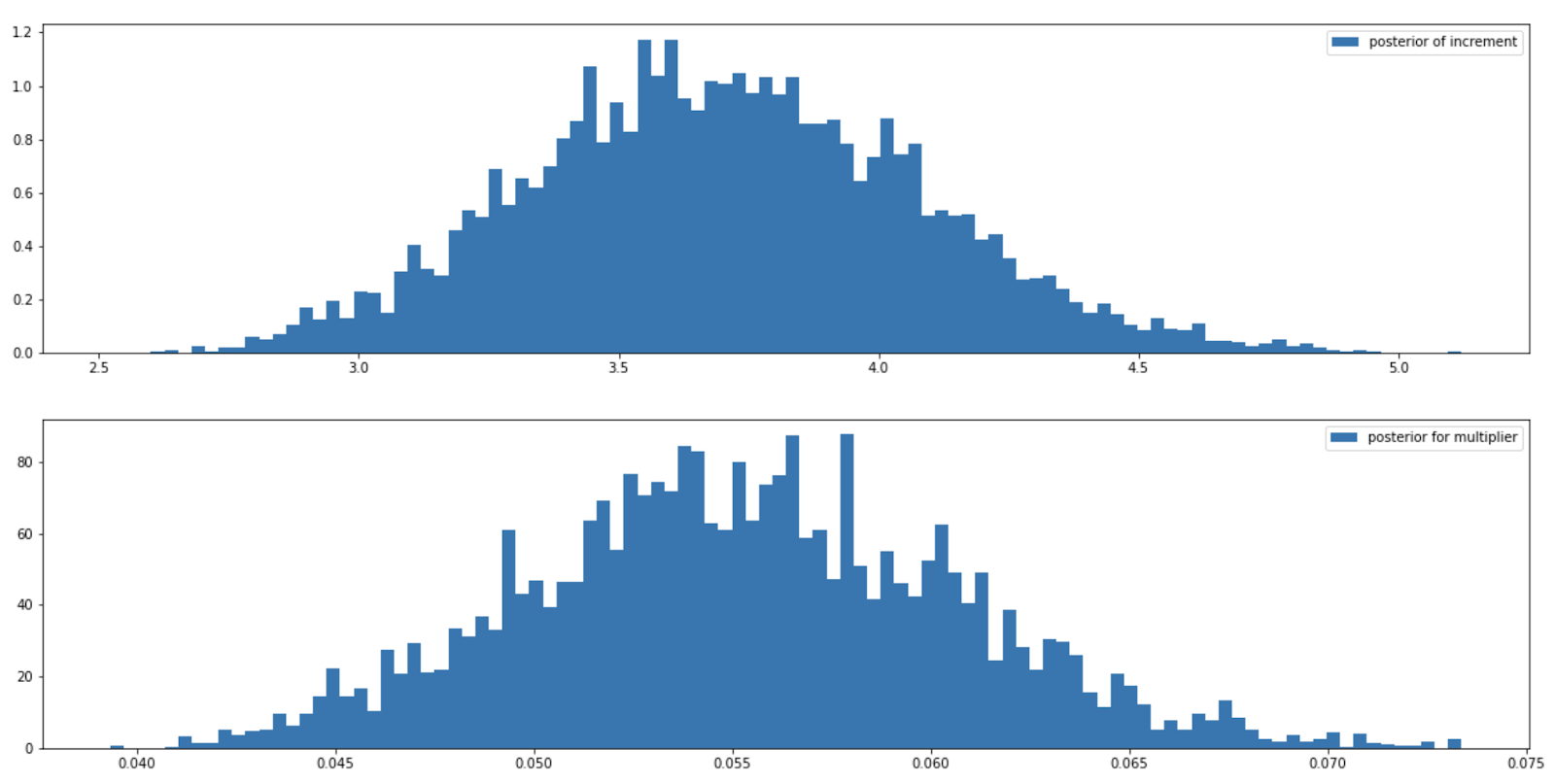

Что мы здесь видим? Во-первых, кажется, что с априорными распределениями мы не ошиблись. Извлечённые выборки действительно похожи на выборки из нормального распределения, нет аномальной скошенности слева или справа. В качестве эксперимента попробуйте либо сильно изменить параметры априорных распределений, либо сами распределения. А во-вторых, выборки для multiplier не покрывают 0. Это означает, что в уравнении сигмоиды (формула 2 в этой статье) не произойдёт зануления при перемножении x (количество дней текущей неактивности) и multiplier. Получается, что вероятность оттока не будет принимать константные значения. Следовательно, можно сделать вывод, что количество текущих неактивных дней действительно влияют на вероятность клиентского оттока.

Так как мы имеем дело с целыми выборками из апостериорного распределения, то и оперировать мы будем матрицами. В связи с этим напишем функцию вычисления сигмоиды, используя матричное умножение, в дальнейшем будем её использовать для визуализации графика:

def make_sigmoid(multiplier, our_data, increment):
    return 1 / (1 + np.exp(np.dot(multiplier, -our_data) + increment))

Давайте подставим все сгенерированные значения в созданную выше функцию make_sigmoid, правильно соблюдая размерность векторов, и получим множество возможных вероятностей оттока в зависимости от текущего количества дней неактивности.

И для извлечения средней вероятности оттока просто усредняем переменную probability_for_inactive_days по 0 измерению. Отрисуем полученный график функций:

mean_probability = probability_for_inactive_days.mean(axis=0)

plt.plot(inactive_days, mean_probability)
plt.xlabel('Current inactive days')
plt.ylabel('Churn probability');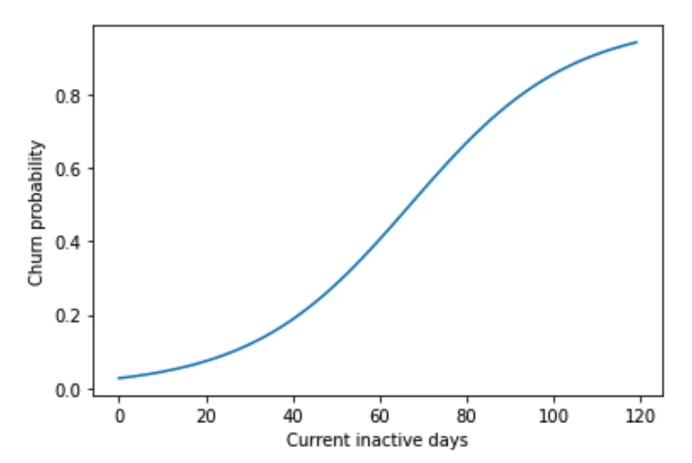

Неплохо: в нашем случае вероятность оттока превышает порог в 0.5 где-то после 65 дней. Давайте внесём больше подробностей путём добавления байесовского доверительного интервала, а также поместим всё это поверх scatterplot, на котором у нас размещались отточники и не отточники.

Я хочу построить 95% доверительный интервал, вы можете выбрать любой другой, какой захотите. Для этого нужно просто извлечь все возможные сигмоиды, которые находятся в переменной probability_for_inactive_days между 0.025 и 0.975 квантилями:

target_quantiles = mquantiles(probability_for_inactive_days, 
                              [0.025, 0.975], axis=0)


plt.figure(figsize=(20, 10))
plt.scatter(data['current_days_inactivity'], 
            data['churned'], label='1 - Churned\n0 - Not churned')
plt.plot(inactive_days, mean_probability)
plt.fill_between(inactive_days, *target_quantiles, alpha=0.5, 
                 label='95% bayesian confidence interval')
plt.xlabel('Current inactive days')
plt.ylabel('Churn probability')
plt.legend();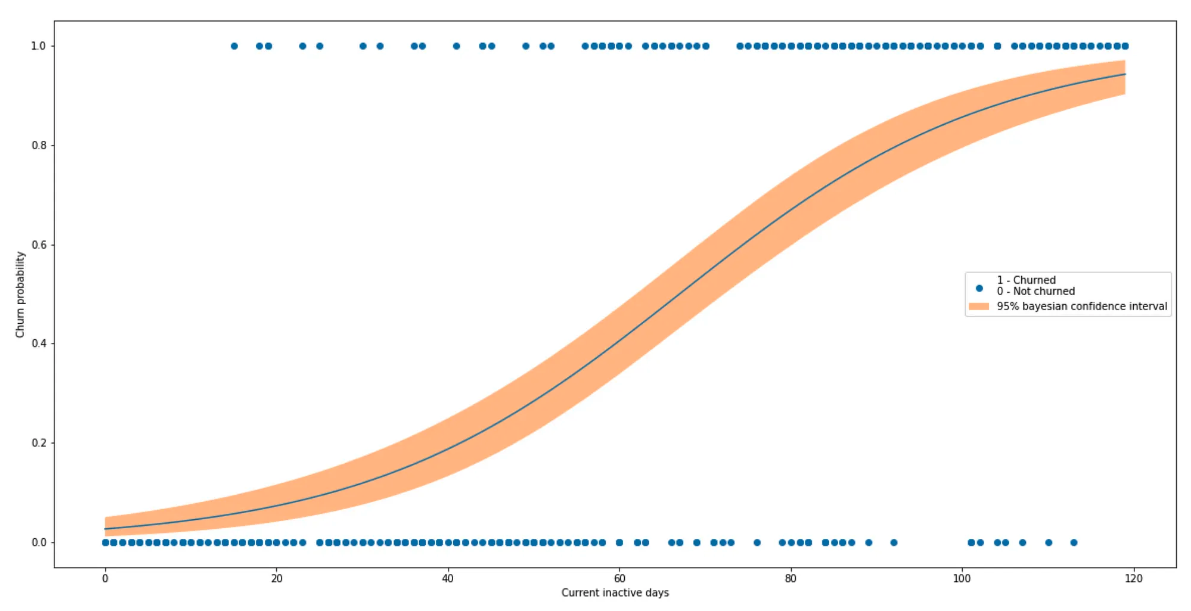

И давайте извлечём больше конкретики по вероятности оттока на определённое количество дней клиентской неактивности:

for i in range(60, 70, 1):
    print('''the probability that a customer has abandoned the service after {0} days of current days inactivity: 
             mean = {1:.0f}%, 95% CI = ({2:.0f}% - {3:.0f}%)'''.format(
        i, mean_probability[i]*100,
         target_quantiles[0][i]*100, target_quantiles[1][i]*100))
    print('=========')

В данном исследовании мы обнаружили, что порог в 67 дней является переломным моментом, после которого, в общем по выборке, можно считать, что клиент, скорее всего, отказался от услуг нашего сервиса, и с ним пора начинать активно взаимодействовать. В вашем кейсе вы можете выбрать совершенного другой порог по вероятности, например, 30%, если вы уверены, что это разумное решение. Но обычно этот порог выбирает бизнес.

Почему мы должны верить построенной модели?

Когда-то британский статистик Джордж Бокс написал: "All models are wrong, some are useful". Очень бы хотелось убедиться, что построенная нами модель полезная. Существует множество различных способов проверить, насколько адекватна модель, и можно ли верить результатам, полученным на её основании. Конкретно здесь мы рассмотрим самый простой, но тем не менее полезный способ валидации — визуальный.

Смысл этой проверки заключается в том, что на основании нашего бернулиевского процесса мы можем сгенерировать различные наборы данных наших клиентов и оценить, насколько сильно они отличаются от исследуемого набора данных. Выглядит это следующим образом:

N = 10000
with pm.Model() as model:
    multiplier = pm.Normal("multiplier", mu=0, tau=0.001, )
    increment = pm.Normal("alpincrementha", mu=0, tau=0.001,)
    probability = pm.Deterministic("churn_probability", 
                                   1.0/(1. + tt.exp(-multiplier*data[
        'current_days_inactivity'] + increment)))
    
    observed = pm.Bernoulli("observed_data", probability, 
                            observed=data['churned'])
    
    simulated = pm.Bernoulli("simulated_data", probability, 
                             shape=probability.tag.test_value.shape)
    
    step = pm.Metropolis(vars=[probability])
    trace = pm.sample(N, step=step)
    
simulations = trace["simulated_data"][:20000]

N = 4

plt.figure(figsize=(20, 10));
for i in range(N):
    plt.subplot(N, 2, i+1)
    sns.scatterplot(data, x='current_days_inactivity', 
                y=simulations[1*i, :], color='black', alpha=0.3)
plt.suptitle("Generated data based on the model")
    
plt.figure(figsize=(20, 3))
plt.title("Our real data")
sns.scatterplot(data, x='current_days_inactivity', y='churned', 
                color='black', alpha=0.3)

Визуально прослеживается паттерн того, что клиенты, которые не являются отточниками, в среднем имеют меньшее количество дней текущей неактивности (скапливаются ближе к левому краю). И наоборот. Также присутствует большая площадь перекрытия посередине, что в целом очень похоже на те данные, которые мы исследуем. Если же мы наблюдаем обратный паттерн, то есть сгенерированные данные отличаются от исследуемого набора, то это первый признак того, что с моделью что-то не так. Возможно, выбраны неверные априорные распределения или неверно подобрана функциональная зависимость отточников от количества текущих дней независимости. В любом случае, такой проверкой не стоит пренебрегать в своих исследованиях, потому что она очень простая и позволяет уберечься от некоторых досадных ошибок.

В заключение

Безусловно, рассмотренный подход нельзя назвать идеальным, а построенную модель — очень точной. В данном случае мы делаем выводы по клиентам на основании всех данных, пренебрегая тем фактом, что каждый из них уникален. Однако в ситуациях, когда мы не обладаем даже какими-либо предположениями о том, когда клиента стоит реактивировать, этот подход может оказаться очень хорошей отправной точкой. Исследование можно выполнить всего за пару часов вместе со временем, потраченным на сбор данных. И тем самым позволить бизнесу начать принимать полезные решения.