Мой сегодняшний рассказ начинается так, что завязка сюжета знакома каждому: с нахождения площади прямоугольного треугольника. Думаю, все прекрасно помнят, что:

Казалось бы, что тут исследовать, и при чём тут передний край науки, нерешенные задачи и величественные гипотезы? Однако, математика - натура обманчивая: здесь сложнейшие проблемы высасываются из пальца могут вырасти на почве формул 6-го класса, а их строгое доказательство может быть завязано на истинность одной из 7 математических задач тысячелетия - гипотезы Бёрча-Свиннертон-Дайера. Именно так произошло и в нашем случае!

Определение

Положительное рациональное число называется конгруэнтным, если оно является площадью прямоугольного треугольника с рациональными длинами сторон.

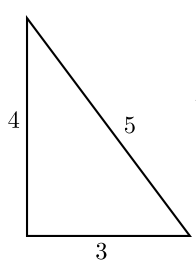
Здесь же возникает резонный вопрос: "конгруэнтное чему ?". Обычно термин конгруэнтный употребляется как синоним к словам "равный, одинаковый", а в нашем случае никаких сравнений нет. Вопросы отпадают, если немного заглянуть в историю.

В 1225 году король Германии Фридрих II попросил Леонардо "Фибоначчи" Пизанского поучаствовать в математическом турнире, специально для которого было заготовлено несколько сложных по тем временам задач.

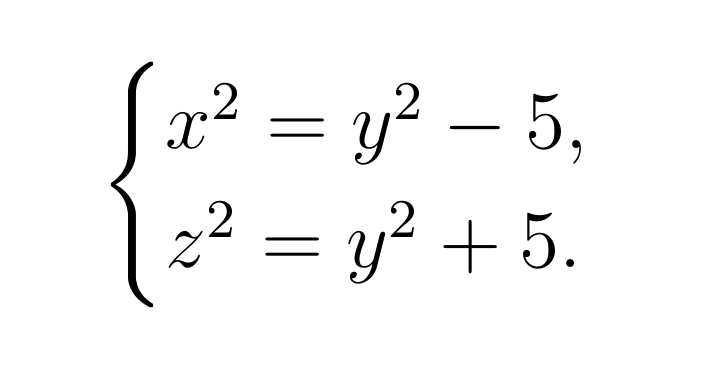
Для простоты давайте перепишем эту систему уравнений в одну строку:

Так вот, разность арифметической прогрессии, члены которой являются квадратами натуральных чисел, называется конгруумом. В данном случае конгруум равен 5. Но как перейти от арифметической прогрессии к прямоугольному треугольнику? Поработаем с указанной выше системой уравнений в общем виде:

И что же мы видим? Правильно, пифагорову тройку! Таким образом, для арифметической прогрессии из трёх квадратов x^2, y^2, z^2 средний член y является гипотенузой прямоугольного треугольника, а два других x и z - суммой и разностью его катетов.

Воспользовавшись известной параметризацией для пифагоровых троек, можно получить общую формулу, позволяющую находить такие арифметические прогрессии и вычислять их конгруумы:

Теперь посчитаем площадь получившегося прямоугольного треугольника:

Таким образом, 60 является конгруэнтным числом, которое соответствует конгрууму 240 и прямоугольному треугольнику (8,15,17).

Минимальное целое конгруэнтное число

Изучением этой проблемы занимался и Пьер Ферма, который доказал, что 1 не является конгруэнтным числом (как обычно использовал метод бесконечного спуска). Со временем стало известно, что числа 2,3 и 4 такими не являются. Наименьшим целым конгруэнтным числом, соответствующим прямоугольному треугольнику с целыми (3,4,5) сторонами является 6. Но ведь есть же возможность, что катеты и гипотенуза будут не целыми, а площадь - целым числом, меньшим 6?

Вернемся к примеру, который исследовал Фибоначчи. Напомню, что в итоге у него получилось следующее:

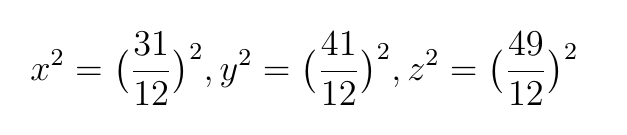
Конгруум равен 5, а вот чему равна площадь соответствующего прямоугольного треугольника? Решим эту задачу в общем виде, найдя выражение для конгруума через параметры m и n:

Теперь для конкретного случая:

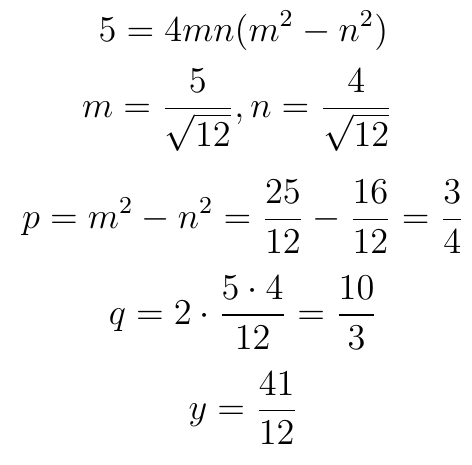
Вычисляем площадь и испытываем разочарование:

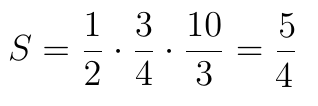
Площадь не является целым числом! Однако, проблемы в этом нет. Посмотрим, что нужно сделать со сторонами треугольника, чтобы его площадь стала равна 5. Оказывается, просто удвоить каждую сторону треугольника:

Правомерно ли это? Конечно да! Домножение на рациональное число оставляет тройку квадратов арифметической прогрессией, меняя лишь конгруум (в случае для нашего треугольника он стал равен 20).

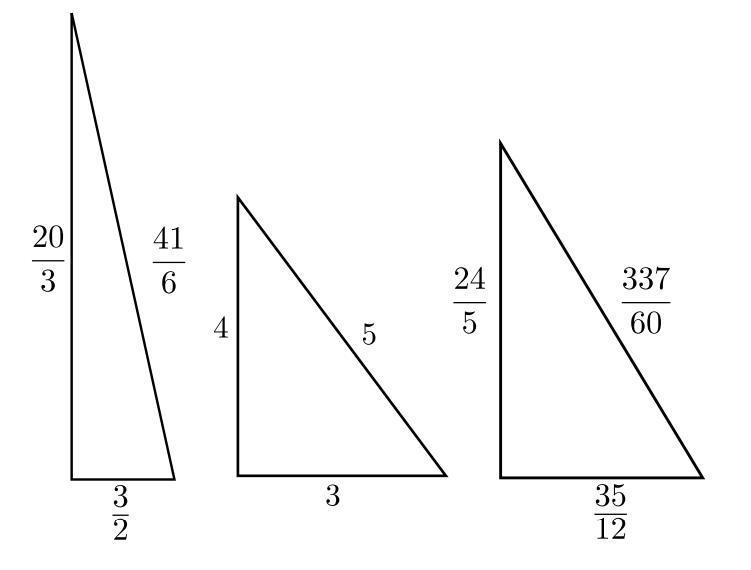
Поскольку конгруум может быть получен (используя параметризацию) как площадь прямоугольного треугольника, каждый конгруум является конгруэнтным числом. И наоборот, каждое конгруэнтное число является конгруумом, умноженным на квадрат рационального числа.

Обратите внимание: чтобы доказать, что 5 является конгруэнтным числом, мы использовали параметризацию, решили нетривиальное уравнение подбором, а потом еще "подрихтовали" результат. Это всё к чему: проверить, что число является конгруумом - легко, а вот определить его конгруэнтность - уже сложнее. Именно здесь вопрос конгруэнтных чисел выходит на передний край науки - алгебраическую геометрию, а конкретнее к теории эллиптических кривых.

Поиск новых прямоугольных треугольников, проверка конгруэнтности чисел и эллиптические кривые

К 1915 году математики определили все конгруэнтные числа, меньшие 100. За последующие 65 лет удалось продвинуться не так далеко - всего лишь до 1000 (и то с пробелами). В 1982 году Джерролд Туннелл из Университета Ратгерса добился значительного прогресса, используя связь между конгруэнтными числами и эллиптическими кривыми.

Пусть {x-n, x, x+n} -три полных квадрата с конгруумом n. Тогда:

Теперь положим y = u*v и получим:

График такой эллиптической кривой выглядит для n=5 следующим образом:

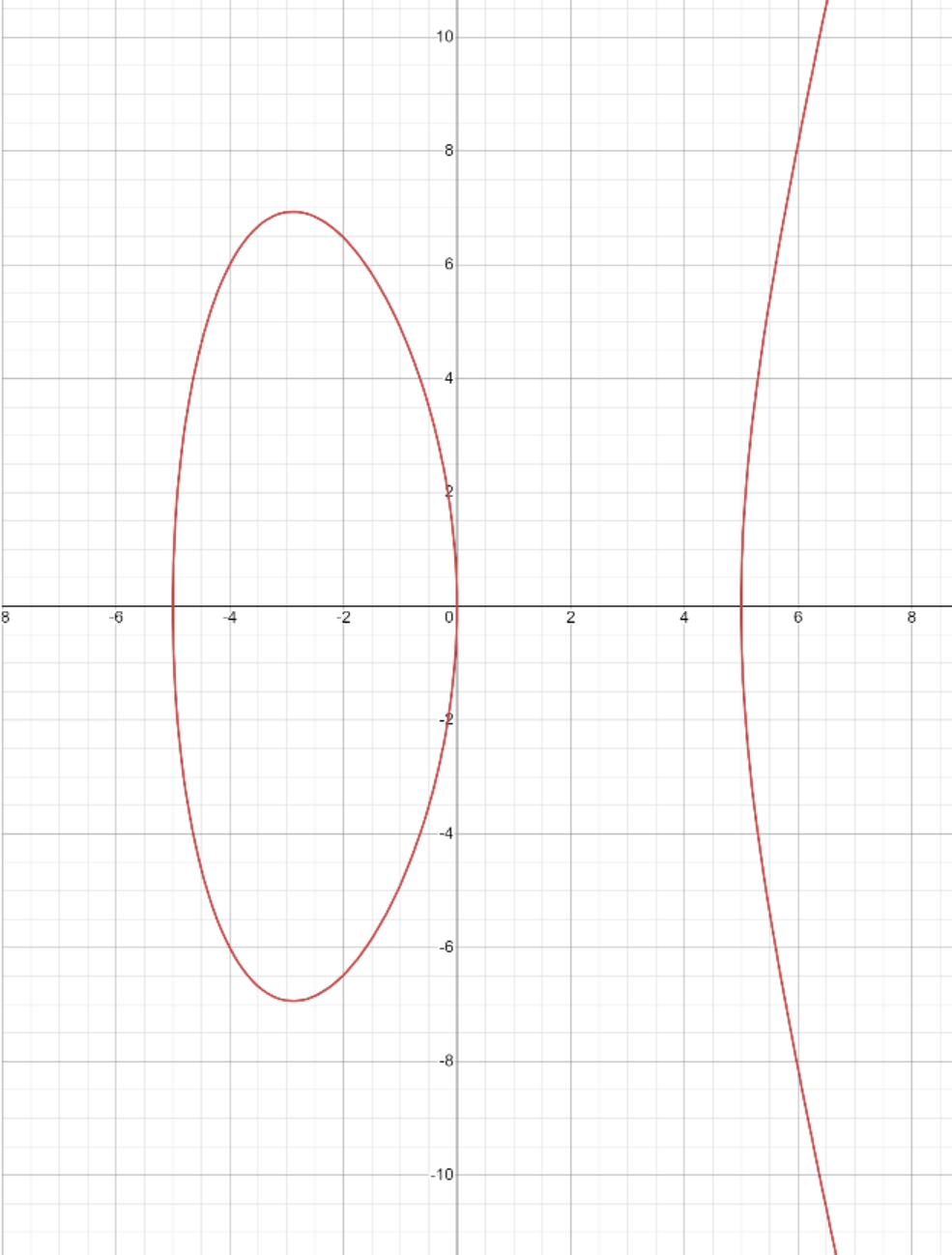
Если рациональные x и y удовлетворяют этому уравнению, то существует двустороннее соответствие:

Тогда, например, для точки (-4;-6) получим знакомый прямоугольный треугольник, но с некоторой особенностью:

Сторона треугольника отрицательная! Впрочем, одно удивительное свойство эллиптических кривых позволит нам одолеть это недоразумение. Оказывается, если провести прямую через две точки кривой с рациональными координатами, то прямая пересечет эллиптическую кривую тоже в рациональной точке!

Что примечательно, этому набору из четырех пар точек всё еще соответствует тот же самый прямоугольный треугольник. Но как найти еще? Да тем же способом! Мы найдем следующую точку А, координаты которой всё так же обязаны быть рациональными:

Её координаты уже не доставляют радости:

Однако, всё компенсируется, когда мы получаем прямоугольный треугольник со сторонами:

площадь которого всё так же равна 5 ! Как Вы уже догадались, этот процесс можно продолжать бесконечно, получая всё новые и новые прямоугольные треугольники, соответствующие конгрууму 5.

Теперь осознайте, что произошло:

1) Мы использовали известный конгруум 5.

2) Априори знали, что он является конгруэнтным числом.

3) Поэтому построили аналитический способ нахождения всё новых и новых прямоугольных треугольников по уже известным начальным данным.

Но что, если мы остановимся на шаге № 1 с вопросом: " А является ли число, например, 157 конгруэнтным?". Как мы будем отвечать на него? К сожалению, математики, простых способов разрешить эту дилемму не нашли.

Тот самый Джерролд Туннелл, впрочем, кое-что придумал. Он составил набор достаточно простых уравнений, которые, если верна гипотеза Бёрча-Свиннертон-Дайера, являются универсальным тестом на конгруэнтность.

Всего лишь нужно понять, сколько троек (x,y,z) удовлетворяет первому и второму уравнению, и если первое число равно удвоенному второму, то n - конгруэнтное число! Несомненно, это одно из самых ярких и простых решений для математических задач, имеющих такую богатую историю. Спасибо, что прочитали!

• Больше математики в Telegram - "Математика не для всех".

Эта статья поддерживается командой ITGLOBAL.COM

Мы — первый облачный провайдер в России, а также интегратор, поставщик ИТ-услуг, продуктов, сервисов и разработчик собственного ПО.  

•  Наш сайт
•  Наш блог про виртуализацию и Enterprise IT
•  Наш YouTube канал
•  Истории успеха наших клиентов