Кватернионы - прекрасный инструмент описания поворотов в трехмерном пространстве. По сравнению с описанием поворотов матрицами, кватернионы обладают несколькими весомыми преимуществами:

1. численная устойчивость;

2. возможность интерполяции;

3. легкость выделения оси и угла поворота из заданного кватернионного представления.

Но есть с кватернионами и проблема... Часто в статьях и туториалах они даются просто как факт: есть такой вот объект и вот так он применяется для поворота вектора . Такой подход оставляет много вопросов:

• почему кватернионы описываются 4-мя параметрами, хотя действуют в 3-х мерном пространстве?

• почему мы считаем оси мнимыми?

• почему мы разбиваем кватернион на 2 части и применяем с двух сторон?

• почему они некоммутативны по произведению?

И как сказано вот в этой публикации:

Мы просто принимаем на веру странные таблицы умножения и другие загадочные определения, и используем их как «чёрные ящики», поворачивающие векторы так, как нам нужно

На самом деле, кватернионы не так сложны и они совсем не черные ящики, если понимать теорию групп. Возможно, именно на таких читателей и рассчитано большинство статей! Шутка :) Я думаю, что самом деле авторы многих статей просто сами не понимают механизм действия кватернионов и «принимают их на веру».

Тех, кто литературе предпочитает кинематограф, приглашаю сюда (не забываем про лайки, подписку и колокольчик):

В данной работе я предлагаю попробовать понять как действуют кватернионы. Шаг за шагом, начиная с простой очевидной геометрии, без гэпов в духе: "вот вам готовый математический объект, пользуйтесь".

1. Что такое повороты в 3D и какая у них размерность?

* 1.1. Модель вращения

* 1.2. Какая размерность у вращения в 3D?

* 1.3 Коммутативность и третья ось

* 1.4 Углы Крылова и углы Эйлера

* 1.5 Матрицы поворота

2. Кватернионы

* 2.1  Мнимые числа и двумерное вращение

* 2.2 Гиперкомплексные числа

* 2.3 Три мнимых оси

* (*)

* 2.4 некоторые свойства кватернионов

* 2.5 Вращаем вектор

* 2.6 Ось и угол вращения

* 2.7 С точки зрения алгебры

* 2.8 Интерполяция поворотов

Заключение

1. Что такое повороты в 3D и какая у них размерность?

1.1. Модель вращения

Для начала, давайте разберемся с решаемой задачей с геометрической точки зрения. Нам нужно понять преобразование, которое мы называем поворотом в 3-х мерном пространстве. И на этом этапе даже "понятные" матрицы поворота нам не подходят.

Давайте рассмотрим глобус!

Думаю, все представляют себе этот девайс, и как он работает: мы вращаем шарик, закрепленный. на оси и смотрим на сферическую карту Земли.

Вращать глобус можно по разному. Рассмотрим такую технику, ставим палец на какую-то точку и перемещаем, не отрывая от поверхности. Очевидно, что двигать палец получится только вдоль параллели. Можно поместить палец в одну произвольную точку и сместить его в другую произвольную (но лежащую на одной параллели с первой точкой). Каждой такой паре точек будет соответствовать какой-то поворот. А множество всех возможных пар точек, таким образом, будут описывать множество всех возможных поворотов шарика вокруг заданной оси. Причем, каждому повороту будет соответствовать целое множество пар точек. Но это не страшно, главное, что все возможные повороты будут учтены :)

Вот такое представление поворотов давайте рассмотри детально. Пусть у нас есть сфера, с центром в начале координат. Радиус сферы примем за единицу. Любое преобразование сферы, не изменяющее ее положения, не меняющее расстояние между точками ее поверхности, не выворачивающее ее на изнанку и отображающее множество всех точек сферы в себя же, будет вращением. На поверхности сферы определим две точкии. Поворот сферы будем описывать как результат преобразования, удовлетворяющего условиям ращения сферы и переводящее точкув точку: (рисунок 1.1).

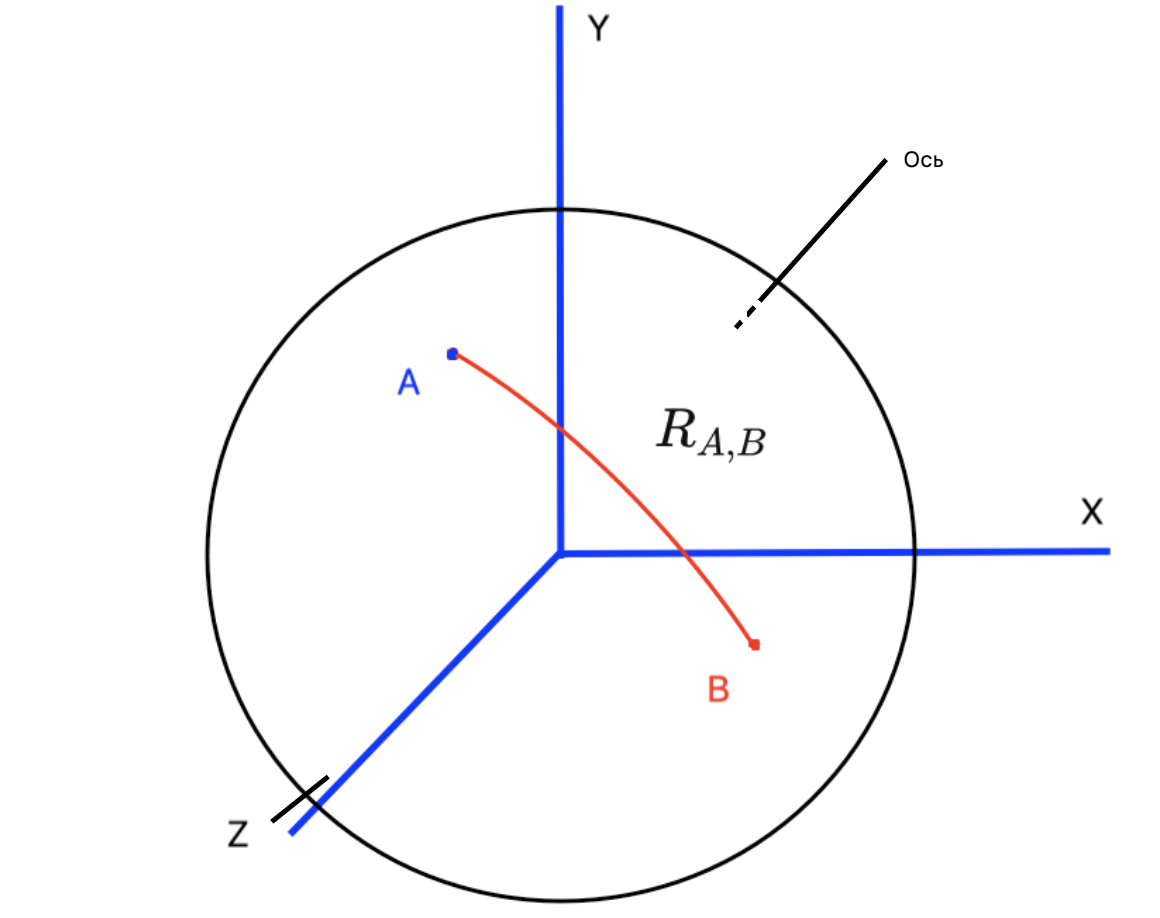
Такой поворот может быть представлен как результат вращения сферы в плоскости , где - центр окружности. Но даже определившись с плоскостью вращения, или с осью (перпендикуляром к ), что в трехмерном случае эквивалентно, нас все равно останется неоднозначность по углам: все повороты на углы , где будут эквивалентны повороту на угол в силу периодической природы вращения. Вернемся чуть позже и к такому определению поворота, а пока поговорим о размерности.

1.2. Какая размерность у вращения в 3D?

Для подсчета степеней свободы произвольного поворота введем такое понятие как поворот вокруг оси : - поворот, не меняющий проекцию точек на ось , где . А также орбиту точки относительно оси : - множество всех точек поверхности сферы, в которые может перейти точка в результате всевозможных поворотов . Это и есть параллель на глобусе, если считать осью Земли.

Теперь рассмотрим орбиты точки относительно осей и : и (рисунок 1.2). - то множества точек, у которых -компонента совпадает с , а - это множество точек у которых -компонента совпадает с . Ось абсолютно равноправна остальным осям, поэтому мы могли выбрать произвольно любые две оси. Наша задача сейчас - показать, что для описания поворотов сферы нам достаточно всего двух осей!

Давайте рассмотрим множество всех точек , в которые может переместиться точка , двигаясь по своей орбите относительно оси . Среди них выделим точки и - точки с минимальным и максимальным значением координаты , среди всех точек соответственно. Для каждой точки рассмотрим орбиту относительно оси : , в том числе и - орбиты относительно оси точек и соответственно (рисунок 1.3).

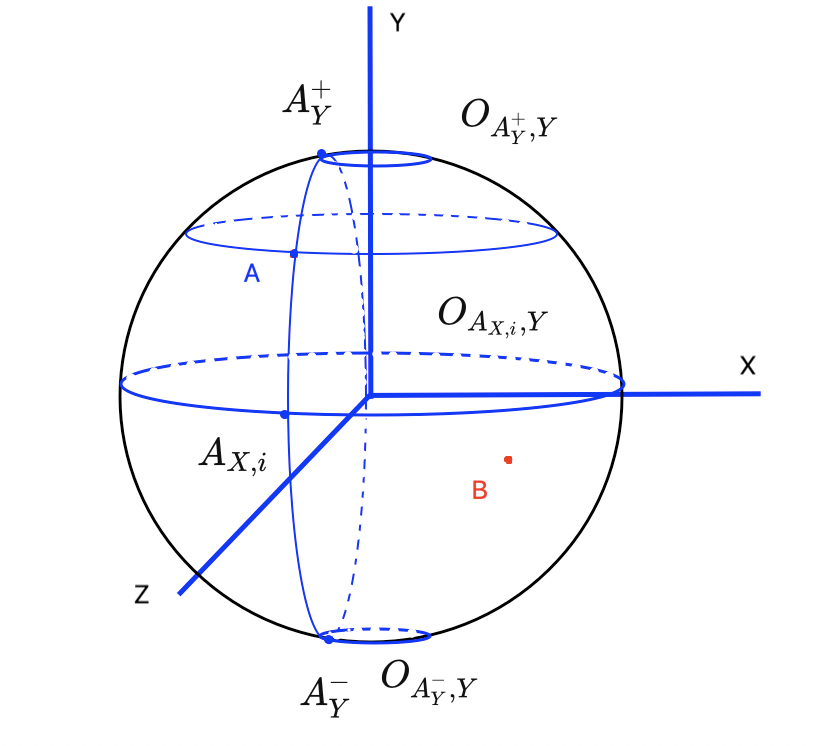
Теперь мы можем найти область сферы , в которую точкаможет переместить в результате композиции двух: поворотов вокруг оси , а затем вокруг оси . Эта область как раз и состоит из всего множества точек орбит . Первый поворот вокруг оси переместит нашу точку в положение точки , а затем поворот вокруг оси переместит ее в любую точку орбиты . Область состоит из всех точек поверхности сферы, ограниченных орбитами и (рисунок 1.4).

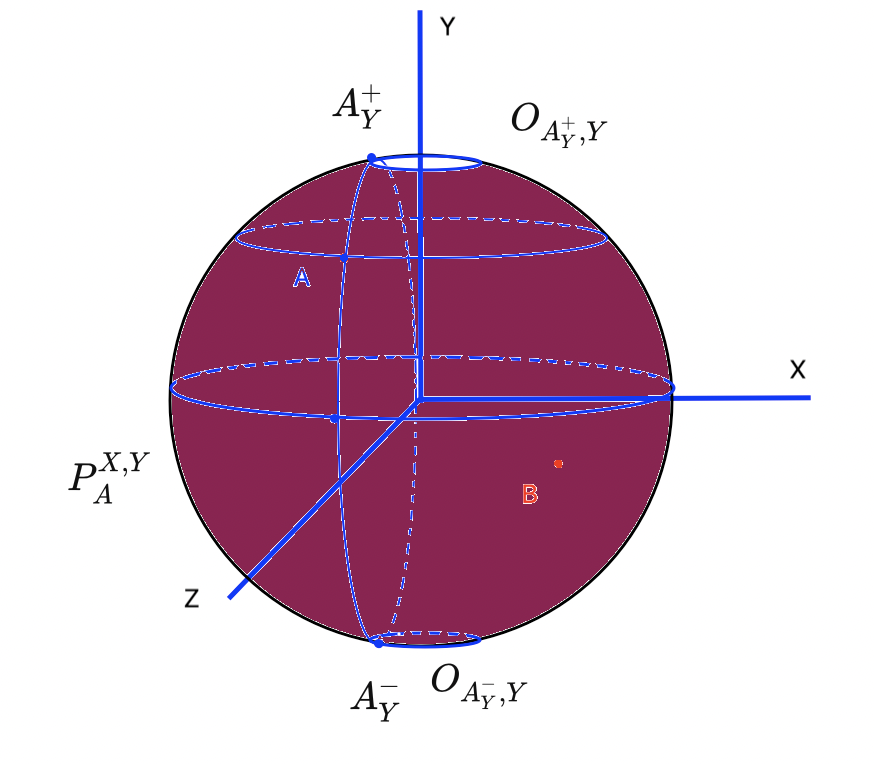
Как видно из построения, точка оказалась в этой области, а значит поворотв данном конкретном случае может реализоваться как композиция поворотов вокруг оси , а затем вокруг оси .

Теперь давайте проведём аналогичные рассуждения для оси . Рассмотрим множество всех точек , в которые может переместиться точка , двигаясь по своей орбите относительно оси . Среди них выделим точки и - точки с минимальным и максимальным значением координаты , среди всех точек соответственно. Для каждой точки рассмотрим орбиту относительно оси : , в том числе и - орбиты относительно оси точек и соответственно.

И найдем область сферы , в которую точкаможет переместить в результате композиции двух: поворотов вокруг оси , а затем вокруг оси . Эта область состоит из всего множества точек орбит . Область состоит из всех точек поверхности сферы, ограниченных орбитами и (рисунок 1.5).

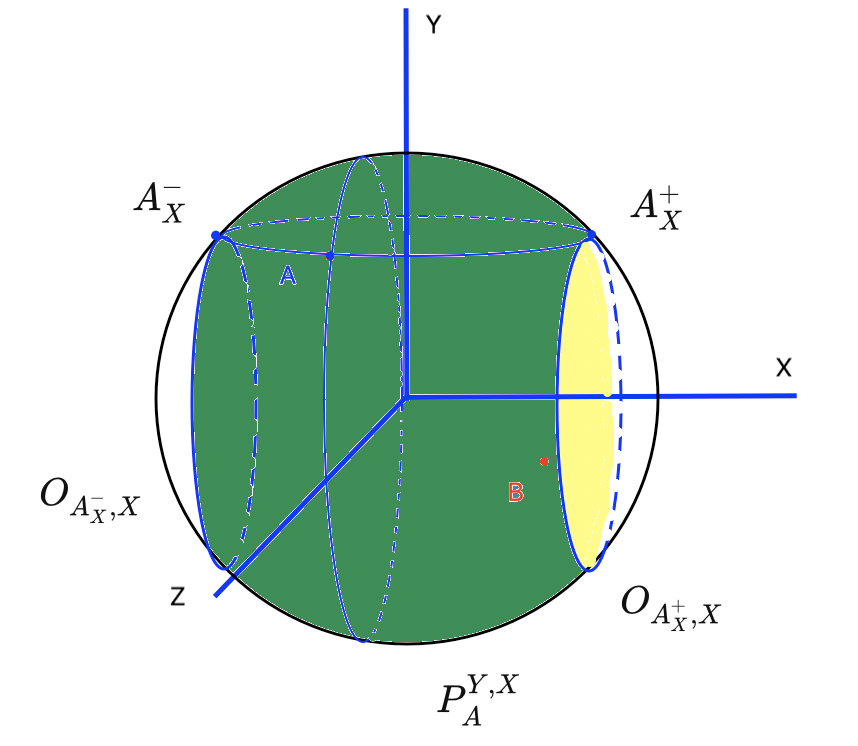
Как видно из построения, точка оказалась и в этой области тоже, а значит поворотв данном конкретном случае может также реализоваться и как композиция поворотов вокруг оси , а затем вокруг оси . Ура, повороты коммутативные! На самом деле нет, но об этом ниже :)

Теперь давайте найдем найдем условия попадания точки в области и .

Как было сказано выше, область ограничена орбитами относительно оси точек и - точек с орбиты относительно оси , имеющих минимальную и максимальную проекцию на ось . То есть, это множества точек, имеющих значения компоненты , совпадающие с минимальным и максимальным значением компоненты , среди точек орбиты . Но учитывая, что весе точки орбиты имеют одинаковую -компоненту и сумма квадратов всех компонент любой точки сферы равна радиусу сферы ( ), экстремальные значения - компоненты точек орбиты будут достигаться при обнулении -компоненты. Тогда можно найти условиях попадания произвольной точки в область следующим образом:

или или

Проведя аналогичные рассуждения для области , мы обнаружим, что эта область состоит из точек , -компонеты которых лежат между значениями -компонент точек и . Которые могут быть найдены как . Таким образом, получаем условия попадания точки на поверхности сферыв область :

или или

Теперь предположим, сто на поверхности сферы есть такая точка , в которую нельзя перевести точку , применив к ней композицию двух поворотов вокруг осей и по одному повороту в любом порядке. Тогда координаты точки должны удовлетворять паре условий: и

Сложим левые и правые части неравенств и получим, что должно выполняться следующее:

, что противоречит условию нахождения точки на поверрхности сферы.

А что это все значит? Это значит, что для перевода точки в любую другую точки поверхности сферы вращением, а значит и для описания любого вращения нам достаточно всего двух элементарных вращений: вокруг оси и вокруг оси в нашем примере. В общем случае это могут быть любые две оси в силу симметрии задачи.

Давайте пока просто запомним этот факт №1.

Любой поворот в трехмерном пространстве может быть описан всего двумя параметрами - углами поворотов вокруг осей и !!!

1.3 Коммутативность и третья ось

Итак, вращение в 3D может быть представлено как двумерное преобразование, мы это показали выше. Любое вращение, преобразующее точку сферы в точку сферы можно представить как композицию вращений вокруг осей и : или , где и - повороты точки вокруг осей и  соответственно.

А можем ли мы утверждать, что вращения коммутативные? То есть утверждать, что ? Очевидно - нет! Ведь если бы вращения были бы коммутативны, то области сферы и совпадали бы. Но в общем случае это не так. Точки, принадлежащие области могут быть получены как преобразование точки только в результате поворота вокруг оси , а затем вокруг оси . Аналогично, в точки области точка может превратиться только в результате поворота вокруг оси , а затем вокруг оси . Таким образом, вращения не коммутативны в принципе! Поэтому даже для области у нас нет основания полагать, что выражения и равносильны, если речь идет о поворотах на одни и те же значения углов!

Несмотря на то, что мы можем описать любой поворот всего двумя углами, пользоваться этой концепцией не всегда удобно, так как приходится отслеживать еще порядок применения поворотов. Отложим эту идею, чтобы вернуться к ней, когда речь пойдет о кватернионах. А пока подумаем, как нам зафиксировать порядок вращений вокруг осей. Но рассмотрим уже все три оси.

Используя выведеденное ранее выражение, получим условия принадлежности произвольной точки области сферы - условие того, что точка может быть получена из точки в результате поворота вокруг оси , а затем вокруг оси . Из соображений равноправности осей и симметричности задачи, поменяем местами индексы и :

или или

Может ли произвольная точка сферы не принадлежать областям и одновременно? Для этого необходимо, чтобы для нее одновременно выполнялись условияи . Сложим левые и правые части этих неравенств и получим, что должно выполняться следующее:

, что противоречит условию нахождения точки на поверрхности сферы. То есть получается, что каждая точка сферы принадлежит либо области, либо области, либо обеим областям одновременно. И что это означает?

А означает это следующее: точка может переместиться в любую точку сферы в результате последовательности трех поворотов в фиксированном порядке: вокруг оси , вокруг оси и вокруг оси . Если точка принадлежит только одной из областей , недостающий поворот можно предполагать формально существующим, но выполненным на нулевой угол.

Таким образом, мы смогли зафиксировать последовательность поворотов вокруг осей, но для того, чтобы покрыть все пространство поворотов нам пришлось задействовать все три оси. В силу симметричности задачи, можно зафиксировать любой порядок осей. Но если использовать все три оси, то такая последовательность элементарных поворотов позволит нам описать любой поворот.

1.4 Углы Крылова и углы Эйлера

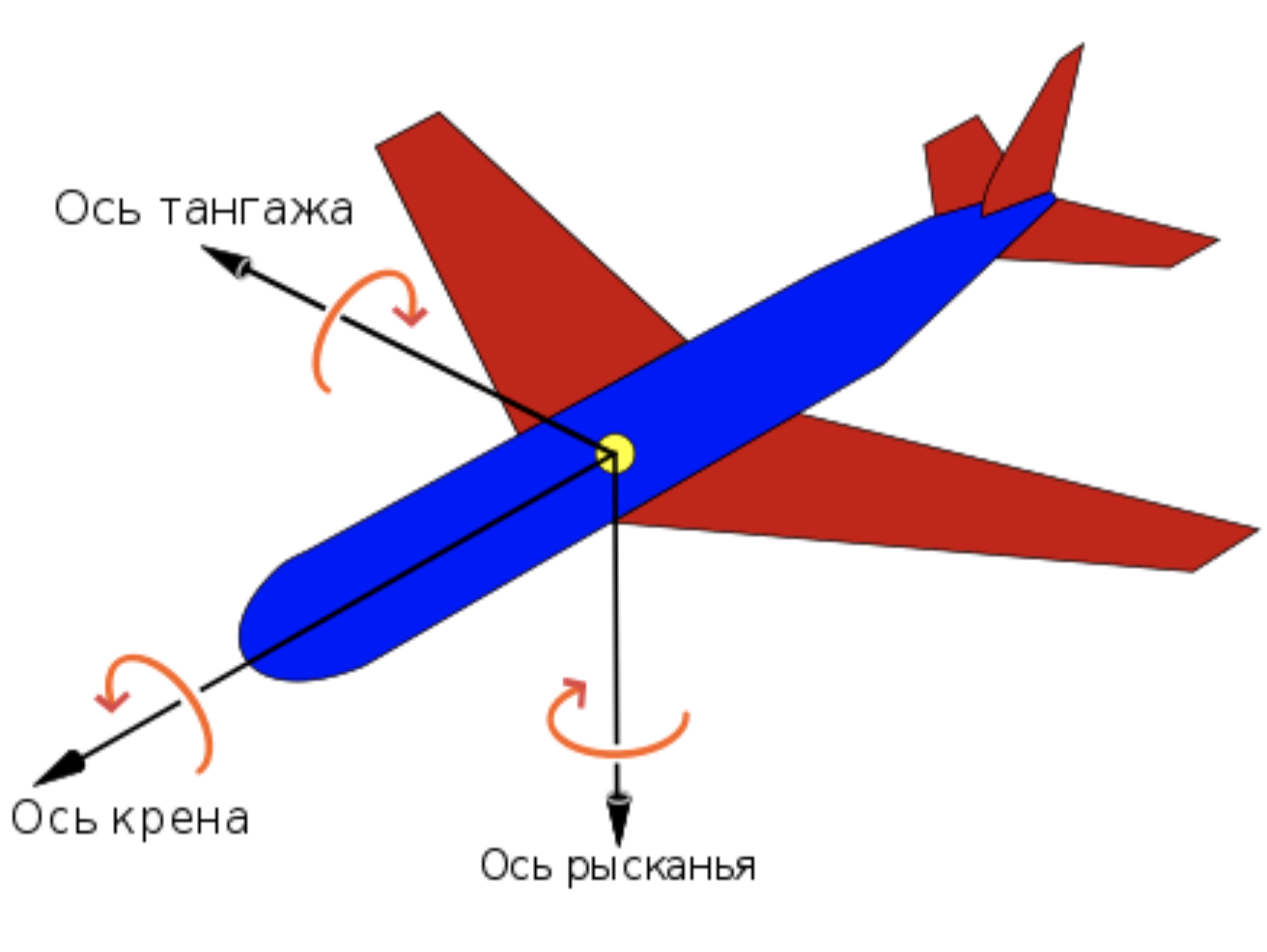
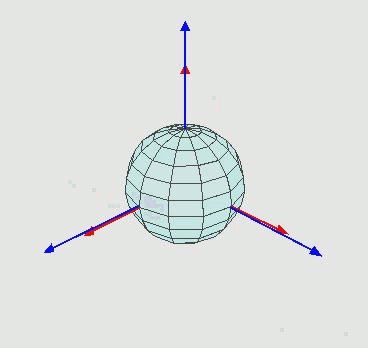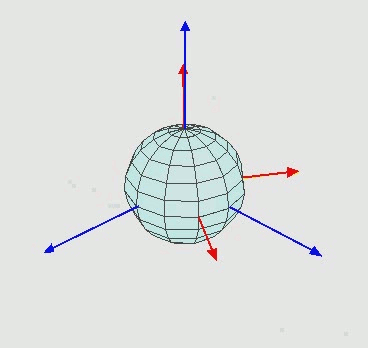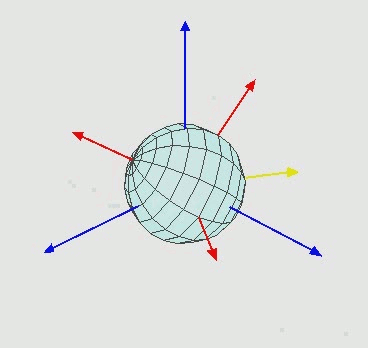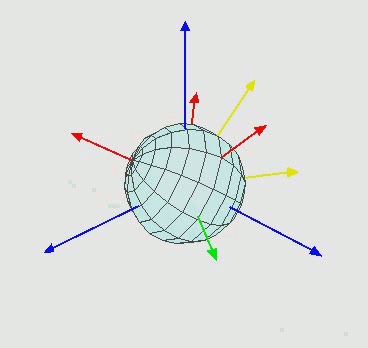
Если для описания ориентации в пространстве плавательного или летательного аппарата ввести ортогональные оси, ориентированные вдоль направления движения, вертикальную, и ортогональную к продольной и вертикальной, то повороты вокруг этих осей будут однозначно описывать итоговую ориентацию объекта (только надо зафиксировать порядок поворотов). Углы этих поворотов называются углами Крылова, а вращения вокруг этих осей называются "лебедь", "щука" и "рак". Постите, не удержался! :)) Нет, эти повороты могут называться по разному, в зависимости от области применения. Например, в авиации они называются "крен (Roll)", "тангаж (Pitch)" и "рысканье (Yaw)" (рисунок 1.6).

Есть в таком подходе к описанию поворотов неочевидный нюанс. После выполнения каждого поворота, две оси системы координат смещаются. Таким образом каждый поворот, кроме первого осуществляется не вокруг первоначальных координатных осей, а вокруг осей, которые трансформируются вместе с изменением ориентации объекта в пространстве - отсюда и название системы Накой системы координат: связанная система координат.

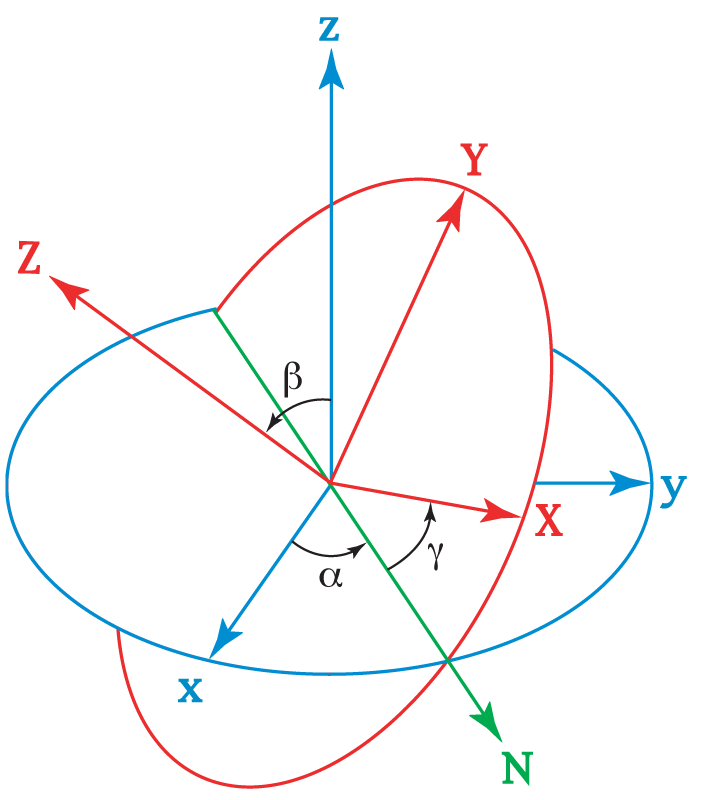
Альтернативой углам Крылова является система углов Эйлера. В системе Эйлера произвольный поворот описывается как поворот вокруг оси на угол - прецессия, затем поворот вокруг оси узлов (это ось, в которую превратилась ось после прецессии) на угол - нутация и вновь вокруг оси (в которую превратилась ось после прецессии и нутации) на угол - собственный поворот (рисунок 1.7 и 1.8).

1.5 Матрицы поворота

Хоть эта публикация и о кватернионах, я все же приведу матричные форма поворотом, чтобы потом можно было оценить всю лаконичность кватернионов по сравнению с матрицами.

Повороты вокруг отдельных осей , , на углы , , соответственно задаются следующими матрицами:

,

,

Результирующий поворот задается матрицей, состоящей их матриц соответствующих поворотов вокруг осей. Поворот, заданный углами Крылова, будет описываться матрицей , а заданный углами Эйлера - (обратите внимание, на два поворота вокруг оси ). Обратите внимание, что у матрицы поворота вокруг оси переставлены местами знаки при синусах. Это особенность оси , связанная с направлением поворота. Поворот в плоскости должен выполняться в направлении от к , Но угол обычно отсчитываю от оси :) В кватернионном варианте, как мы увидим, тоже ось немного отличается.

Ну, и наконец запишем для полного драматизма матрицы поворота вокруг произвольной оси , на угол против часовой стрелки:

,

где

Главное, что мы смогла найти представление произвольного поворота. Но матричное представление оставляет вопросы:

• во-первых, совсем не тривиальная задача найти ось и угол результирующего поворота по заданной матрице;

• во-вторых, как построить интерполяцию между двумя поворотами, заданными в матричном виде? В матричном виде никак, надо искать ось и угол - смотри "во-ревых";

• в-третьих, в статьях встречаются упоминания о том, что матрица обладают низкой численной устойчивостью, а значит плохо подходят для интегрирования поворотов. Например, задача состоит в том, чтобы найти результирующее преобразование серии поворотов. Если таких поворотов много, то в матрице начнут накапливаться ошибки и результирующий поворот может оказаться некорректным.

Но не смотря на эти вопросы, хочется сказать в оправдание матриц поворота, что удобный инструмент для аналитической работы с преобразованиями пространств. Матрицы поворота легко выделить из аффинного преобразования, например.

2. Кватернионы

2.1  Мнимые числа и двумерное вращение

Итак, с постановкой задачи ознакомились, вариант ее решения через матрицы рассмотрели, недостатки выявили, теперь идем в кватернионы. Но сначала рассмотрим более простой вариант: обычную мнимую единицу и ее вращательные возможности для 2D-задачи.

Мнимая единица появляется при попытке решить уравнение . Можно доказать, что решений этого уравнения нет среди действительных чисел. Поэтому мы вводим новый математический объект, который называем мнимой единицей, обозначаем и определяем так: . Заодно сразу введем понятия мнимого числа: и комплексного числа: , где -действительные числа.

Тут есть соблазн сразу вспомнить про свойства комплексных чисел, в частности про формулу Эйлера: , многие авторы так и делают. Но это как раз то, с чем мы боремся :) Поэтому сначала докажем эту формулу, а потом уже поговорим про вращение.

Для начала вспомним, что представляет ряд Макларена (ряд Тейлора в окрестности 0) функций синуса, косинуса и экспоненты:

Теперь подставим в формулу экспоненты вместо , перегруппируем степени так, чтобы нечетные степени имели отдельный множитель , в четных степенях учтем свойство . Затем вынесем за скобки и увидим, как у нас соберутся ряды для синуса и косинуса:

Как видим, это никакая не магия, а обычная алгебра. Теперь вспомним еще некоторые определения, связанный с комплексными числами.

Так как не принадлежит множеству действительных чисел, ни одно число вида  не может быть линейно выражено через действительные числа. А это значит, что значения и являются линейно независимыми. Поэтому мы не можем комплексному числу поставить в соответствие точку на какой-то числовой оси, в отличие действительного числа. Но можем поставить в соответствие точку на плоскости, в которой заданы две ортогональные оси: ось действительных () и ось мнимых чисел (). Но, если на плоскости задана декартова система координат, можно ввести и полярную систему. Тогда комплексное число будет описываться своим абсолютным значением и углом отклонения от положительного направления действительной оси против часовой стрелки - этот угол называется аргументом комплексного числа (рисунок 2.1).

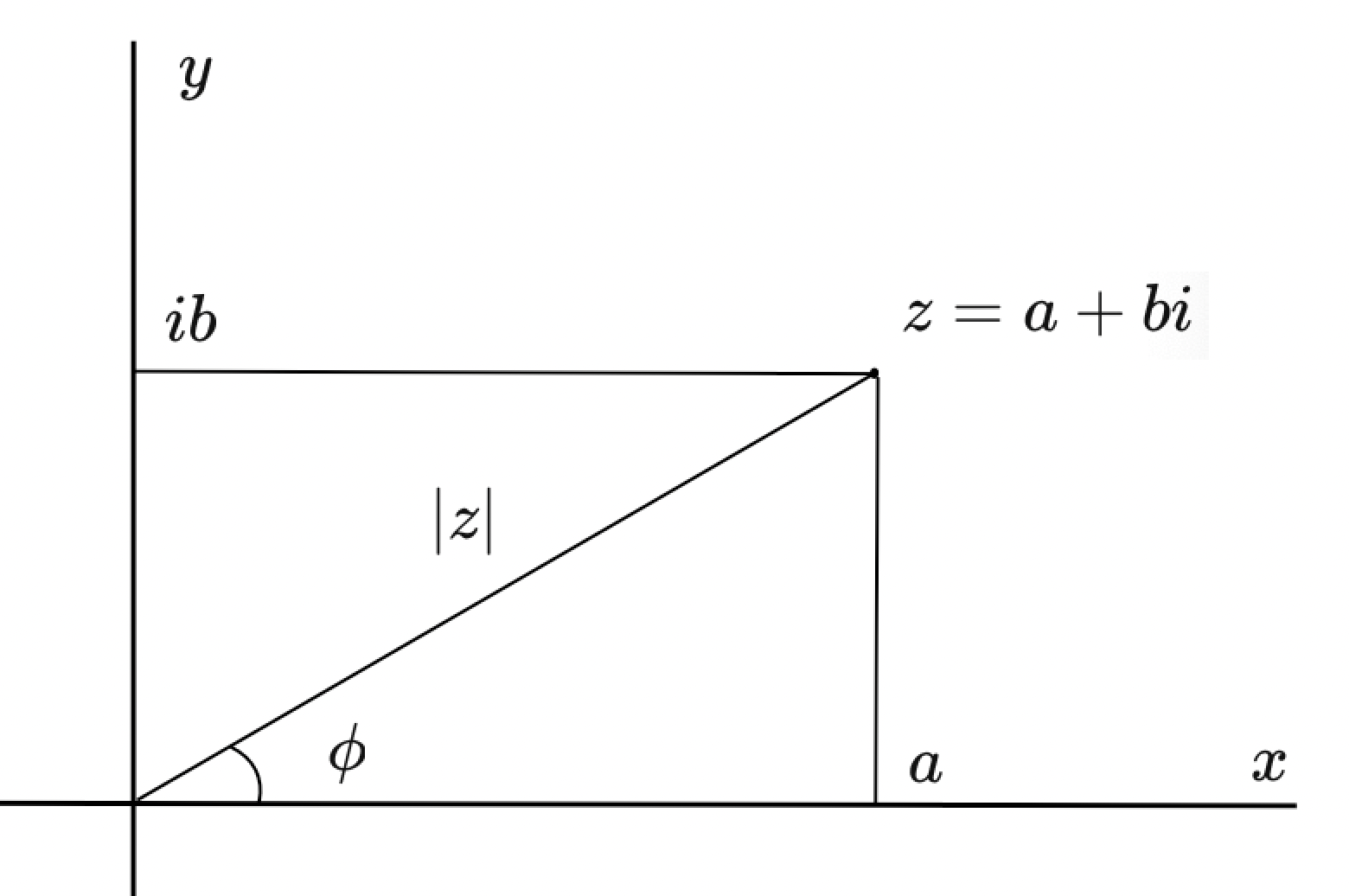
По формулам, связывающим полярную и декартову системы координат, можем утверждать следующее: , . А значит , что по формуле Эйлера дает нам выражение .

А вот теперь можно и повращать! Если мы хотим повернуть точку на комплексной плоскости вокруг начала координат на угол , то нам надо комплексное число, соответствующее вращаемой точке, умножить на : . Как видим, аргумент числа изменился на значение . Если , то множитель .

Давайте пока запомним этот факт №2: чтобы применить поворот на угол , мы его превращаем в множитель вида !

Ну и еще несколько соотношений, которые нам понадобятся в исследовании кватернионов. Если мы возьмем число , то есть число с такам же моделей, как у , но с противоположным по знаку аргументом (повернутое на такой же угол, но в противоположном направлении), то такое число будет называться комплексно-сопряженным к , оно будет отличаться знаком мнимой части: . Очевидно, что число является комплексно-сопряженным к числу , а сама операция комплексного сопряжения является самообратной. Произведение числа с его комплексно-сопряженныйм даст нам квадрат модуля: .

Тогда можно сконструировать обратное число к: (полагаем ).

Произведения чисел ив любом порядке даст нам :

. Само число является обратным к .

Если , то . Это как раз выполняется для комплексных чисел вида . Преобразование, обратное повороту - поворот в противоположную сторону на тот же угол .

Также заметим, что произведение комплексных чисел коммутативно: . И еще одно вроде бы очевидное замечание: - такая конструкция выполняет поворот комплексного числана угол . А можно ли выполнить поворот комплексного числа на угол , используя множитель ( ), который в общем случает имеет отличную от 0 абсолютную величину? Можно! Для этого нужно сделать следующее:

.

Или можно даже так, в силу коммутативности произведения комплексных чисел: . Пока не понятно, зачем так сложно, но позже это нам пригодится. Это уже даже чем-то похоже на действия с кватернионами :)

2.2 Гиперкомплексные числа

Теперь попробуем обобщит эту концепцию описания поворотов на трехмерный случай. Из факта №1, который мы запомнили ранее, следует, что нам нужно сделать два независимых "вращателя". Значит одной мнимой единицей мы ника не обойдемся. Давайте предположим, что существует два "сорта" мнимых единиц и : , но . Каждая из них по отдельности порождает обычную систему комплексных чисел. Но эти системы комплексных чисел ассоциируется с разными плоскостями и оси, соответствующиеи - ортогональны, то естьне может быть линейно выражено через и наоборот. И можно даже построить гиперкомплексное число, у которого будет две мнимые части! На рисунке 2.2 показаны комплексные числа из них разных систем, и .

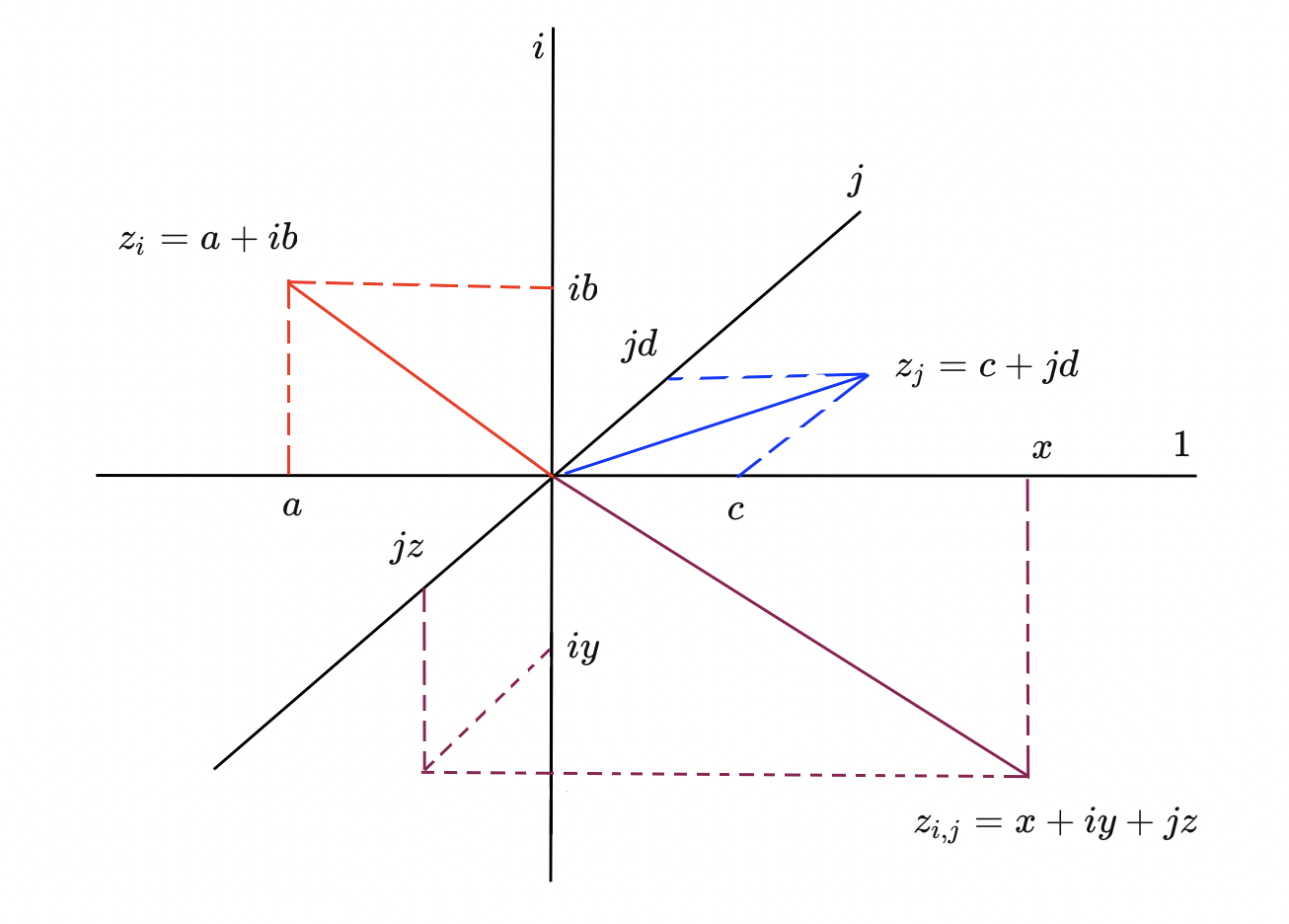
Ура, теперь мы можем произвольный поворот описать через два угла поворота в виде или , останется только умножить эти "вращатели" на какое-то представление поворачиваемого вектора в гиперкомплексном виде!

На самом деле, так и есть! Это и есть описание произвольного поворота в комплексном виде. Но есть нюанс! Не может существовать пространства только с двумя комплексными единицами. Мы будем вынуждены ввести третью!

2.3 Три мнимых оси

Ну вот все же было хорошо, почти построили поворот. Зачем нам третья мнимая единица?

Проблема возникает при попытке расписать выведенное нами выражение поворота:

Вот что за множитель при последнем слагаемом? Может не надо вводить для него отдельную мнимую единицу? Может он как-то может выразиться линейным образом через , и ? Нет! И мы это сейчас докажем.

Существует много разных подходов разной сложности и глубины погружения в теорию групп к доказательству того, что не может быть пары мнимых единиц без третьей. Я предлагаю рассмотреть очень простое и понятное доказательство "для простых смертных". Я его нашел тут.

Предположим, что можно выразить как: , где - действительные числа. Домножим выражение слева на и вспомним, что : . Теперь подставим во второе слагаемое правой части : . Откуда получим:, и . Если первыми двумя выражениями можно как-то жить, то утверждение противоречит изначальной посылке о том, что - дейтвительное число. А значит мы пришли к противоречию инелья выразить как: , где - действительные числа. Значит нам нужно вводить еще один объект, не являющийся действительным числом. Попробуем найти его среди мнимых единиц, предположим, что есть третий "сорт" мнимых единиц: . Ну собственно проверять законность такого предположения мы не будем, просто попробуем построить повороты в такой системе. И если все будет успешно, значит наше предположение о существовании - оправдано :)

Поисследуем это явление. Найдем, чему равно : . Вот это и есть знаменитое открытие Гамильтона: . Отсюда следуют все превращения мнимых единиц друг в друга.

Домножим слева на :

Теперь домножим слева на : . Упс, как говорится! Оказывается наши мнимые единица не коммутативные по произведению, а антикоммутативны: , но ! В общем-то, для задачи описания поворотов - самое то. Предметная область то у нас тоже некоммутативная :)

И выражений и , домножая их слева и справа на и найдем остальные соотношения: , , , .

Это и есть та самая загадочная таблица умножения, которую тяжело принять на веру, не понимая откуда что произошло (рисунок 2.4).

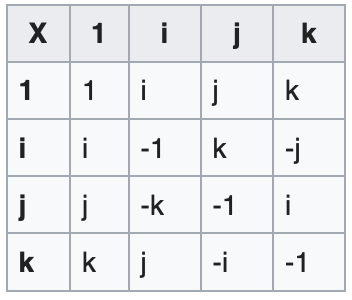
Ну, и еще раз попробуем расписать произведение двух комплексных чисел и , построенных на основе разных единиц:

Как видим, такое гиперкомплексное число состоит из 4-я линейно независимых слагаемых, отсюда и название "кватернион".

(*)

Для больших любителей теории групп и линейной алгебры можно привести другое доказательство существования и его свойств. Это не относится к основной нити повествования, лирическое отступление со звездочкой, так сказать.

Обычную единицу и мнимую можно представить в матричном виде:

, .

Эти объекты удовлетворяют необходимыми нам свойствами: линейная независимость, коммутативность по сложению, коммутативность по произведению и

.

Как нам построить аналогичным образом матричное представление для набора ? В варианте - никак! А в варианте ? Тоже никак! Только в варианте , используя механизм блочных матриц можем сконструировать, например вот такое:

Тут, как и в варианте выполняются соотношения:

Но, если мы захотим посчитать выражение , то получим вот такю конструкцию:

Все взаимопревращения мнимых единиц в таком матричном представлении и антикоммутативность произведений тоже выполняются.

2.4 некоторые свойства кватернионов

Итак, мы ввели понятие кватерниона. Это конструкция в четыре мерном пространстве. Как нам его соотнести с нашим пространством трехмерным? Очевидно, из четырех осей пространства кватернионов надо выбрать три оси. Какие именно? Можно было бы взять одну действительную ось и две комплексные, но это не логично с точки зрения равнозначности осей. Поэтому соотнесем комплексные оси с координатными осями 3D-пространства.

Таким образом, кватерниону можно поставить в соответствие вектор в трехмерном пространстве и одно скалярное число. Может показаться, что действительная ось тут избыточна, мы ведь собираемся заниматься геометрией в трехмерном пространстве. Но на самом деле эта ось нам понадобится.

Мнимые единицы в геометрической интерпретации кватерниона соответствуют единичным векторам, определяющим оси , и - ортам , и . Векторные произведения ортов соответствуют произведениям мнимых единиц: , , , , , . Что подтверждает правильность выбора трех мнимых осей кватерниона для описания осей 3D-пространства.

Это, на самом деле, и есть основной довод в пользу того, чтобы сопоставить трем осям пространства мнимые единицы. Слово мнимые не должно пугать. Ведь в математике мнимость не означает "ненастощесть", как в литературном варианте употребления этого слова. Мнимый в математике - это обладающий определенным набором свойств и не более того.

Таким образом получается, что кватернион можно интерпретировать как набор четырех чисел, три из которых умножаются на мнимые единицы и как вектор и скаляр , где . В любой интерпретации у кватерниона выделяется действительная часть, а остальные слагаемые образуют мнимую или векторную часть.

Другие форма представления кватерниона связаны с возможностью выделить одну из комплексных единиц (любую) как общий множитель двух слагаемых: , важно соблюдать порядок умножения комплексных единиц. Ну и еще одна форма представления, это та, с которой мы начинали: . Эти формы задействую только две мнимые единицы.

В зависимости от задач удобно использовать разные формы представления кватернионов. Умножение на скаляр выполняется тривиально в любой форме представления: умножается каждая компонента. Для сложения и разности кватернионов удобны векторная и комплексная формы.

Для произведения кватернионов удобно использовать векторную форму. Пусть у нас есть кватернионы и , тогда , где - скалярное проиведение и . Это выражение можно получить из комплексной формы кватерниона, аккуратно раскрыв все произведения и выделив общие множители. Оставим это для самостоятельной работы :)

Как и в случае комплексных чисел, для кватерниона определена абсолютная величина и комплексно-сопряженный . Операция сопряжения само-обратна. Абсолютная величина комплексно-сопряженных кватернионов одинакова, а отличаются они знаком векторной части. Произведение комплексно-сопряженных кватернионов равно квадрату их модуля:

Также можно определить обратный кватернион: .

Несмотря на то, что произведение кватернионов не коммутативно, кватернион и обратный к нему можно умножать в любом порядке: . Если абсолютная величина кватерниона равна единице, обратный кватернион совпадает с комплексно-сопряженным: .

Что к касается сопряжения и произведения, то можно вспомнить такое свойство: , это легко можно доказать, не будем тут расписывать.

Лучше подробно рассмотрим частный случай этого свойства, назовем его "переход через мнимую единицу". Пусть у нас есть неполный кватернион без одного из мнимых слагаемых например без : . Также пусть у нас есть еще один неполный кватернион, состоящий только и одной компоненты, которая отсутствует в : . Тогда мы можем менять их местами в произведении, выполняя сопряжение только :

Этот трюк нам понадобится для понимания поворотов.

Ну, а теперь давайте наконец-то вращать!

2.5 Вращаем вектор

Первое, что нам надо сделать, чтобы вектор мог как-то взаимодействовать с кватернионами поворота - это представить вектор в виде кватерниона . Ну, с векторной частью все довольно просто - она равна . Но что делать со скалярной частью, каткое там должно быть значение? Почти во всех источника утверждается, что вектор в кватернионной представлении должен обладать нулевой скалярной частью: . Но на самом деле, в скалярную часть можно записать любое значение, оно останется неизменным при повороте векторной части. Пока давайте будем предполагать общий случай , где -  произвольное действительное число. Значение действительной части кватернионного представления преобразуемого вектора мы постигнем, когда будем говорить про бикватернионы (в следующей публикации). Итак, представляем вектор как кватернион: .

Как мы выяснили ранее, любой поворот вектора можно реализовать через повороты вокруг осей. Рассмотрим поворот вокруг оси на угол . Что должно произойти с вращаемым кватернионом ? Его скалярная часть и проекция на ось должны сохраниться неизменными, а проекции на оси и должны поменяться, мы ведь выполняем поворот в плоскости . Разобьем на два слагаемых: . Теперь вспомним, что и вынесем за скобки во втором слагаемом: . Вращаем вокруг оси , поэтому вращающий множитель построим с мнимой единицей: . согласно установленного раньше факта №2. Умножим на кватернион слева (можно попробовать и справа, столкнемся с аналогичными сложностями): . Со вторы слагаемым все хорошо, комплексное число действительно повернется на угол при умножении на . Но вот с первым слагаемым проблемы. Наши скалярная часть и компонента тоже повернулись как комплексное число. Надо придумать. как действовать вращателем только на второе слагаемое...

Решение такое: разобъем угол пополам и используем мнимую единицу при втором слагаемом для изменения сопряженности множителя справа, мы называли это переходом через мнимую единицу. То есть сделаем так: . Тогда со скалярной частью и -компонентой ничего не произойдет: . А с проекцией на плоскость произойдет требуемый поворот поворот: , что и требовалось.

Таким образом, чтобы выполнить поворот вокруг оси на угол мы вводим кватернион . И чтобы повернуть , мы выполняем операцию .

Аналогичной цепочкой рассуждений можно показать, что поворот на угол вокруг оси выполняется кватернионом : . В этом случае вращаемый кватернион мы разбиваем на такие слагаемые: , первое из которых должно остаться неизменным, а второе повернуться. Тут надо обратить внимание, что в случае оси , поворот осуществляется как бы в обратную сторону, что видно из необычного порядка слагаемых в или необычного положения мнимого множителя в. Это особенность оси , поворот вокруг нее выполняется от оси к оси . Либо в обратном направлении, но на противоположный угол :)

Ну, и наконец, ось . Для поворота на угол вокруг оси мы вводим кватернион . Сам поворот выполняется аналогично: . Чтобы понять его механизм, разбиваем кватернион следующим образом: , первое слагаемое остается неизменным, а второе поворачивается как комплексное число.

Ну, и как мы ранее выясняли, любой поворот можно описать двумя поворотами вокруг ортогональных осей. Поэтому кватернион любого поворота можно представить в виде либо в виде , для некоторых поворотов доступна только одна из этих форм. Как это работает? Возьмем для примера второй вариант и применим его к ( только еще вспомним свойство сопряжения произведения кватернионов):

Что, очевидно, является поворотом вокруг оси , того, что получилось после поворота вокруг оси . Из этого примера вы видим, что цепочка последовательных поворотов может выражаться одним кватернионом, который строится как произведение кватернионов соответствующих поворотов. Для углов Крылова и углов Эйлера тоже можно поставить в соответствие кватернионы и соответственно.

Ну, и последний штрих. Для всех кватернионов, которые строятся из поворотов, заданных в виде экспонент, всегда будет выполняться условие . Но на самом деле поворот вектора можно выполнить и не единичным кватернионом, аналогично тому, как мы это делали для комплексных чисел. Только в этом случае права множитель будет не просто комплексно сопряженным, а обратным: пусть и ( ).

Тогда . Это более общий случай, но если строить кватернионы только из экспонент и их произведений, то можно оставить только сопряжение.

2.6 Ось и угол вращения

Ну вот выполнили мы ряд поворотов, получили через произведения кватернионов этих поворотов кватернион итогового поворота. И согласно ранее остановленного факта №1, это все эквивалентно одному итоговому повороту. А как из кватерниона выделить итоговый поворот в виде оси, вокруг которой выполняется итоговый поворот, и значения угла?

Для ответа на этот вопрос давайте зайдем с другой стороны. Пусть задан поворот в виде оси единичной длины () и угла поворота вокруг этой оси по часовой стрелке . Представим эту ось и угол в виде одного вектора, сонаправленного с осью вращения и с длиной, равной углу поворота: . Именно таким образом в физических задачах задается вращение.

Теперь еще раз вспомним установленный раннее факт №2, утверждающий, что поворот в комплексной плоскости на угол осуществляется множителем . Учитывая, что повороты в 3D описываются аналогичными комплексными категориями, кватернион поворота должен являться экспонентой некоторой величины. Очевидным кандидатом на аргумент экспоненты как раз и является - это ведь и есть количественное выражение поворота. Но, в отличие от , его не нужно умножать на мнимую единицу и вот почему: экспонента мнимой величины периодична, что соответствует природе вращения. Собственно, это и объясняет, почему в выражении при стоит множитель . Что касается осей трехмерного пространства, мы их объявили мнимыми, а значит вращение вдоль любой оси автоматически периодично.

Значит нам надо построить кватернион поворота как экспоненту . Для этого мы превращаем в кватернион и ищем кватернион поворота как . Деление на 2 тут по той же причине, по которой мы делили пополам углы, кватернион будет применяться по схеме .

Осталось только понять, как найти экспоненту от кватерниона... Так через ряд Макл jрена же! Для простоты, давайте найдем , а с делением пополам потом разберемся. Итак:

Единицу представили как кватернион с нулевой векторной частью и единичной скалярной. Для дальнейших рассуждений за метим две вещи.

Вещь первая.  Пусть вектора и коллинеарны ( ) тогда кватрнионы без скаларных частей, но с оответствующими векторными частями будут умножаться следующим образом:

Вещь вторая.  Пусть у нас есть два кватерниона, один без скалярной части , а второй без векторной . Тогда их произведение:

С учетом этих замечаний становится понятно, что в степенях будут чередоваться кватернионы без векторной части (для четных степеней) и без скалярной (для нечетных степеней):

,

И так далее, получаем чередование безвекторных и безскалярных неполных кватернионов, чередование знаков через две степени и растущую степень . Теперь еще раз запишем разложение экспоненты в ряд, но с учетом формул для степеней:

Теперь соберем э этого всего один кватернион, учитывая линейность его компонент, и вынесем за скобки в векторной части:

Как видим, а скалярной и векторной частях сформировались ряды Макларена косинуса и синуса соответственно. И мы можем записать итоговое выражение: . Это кватернион с единичным абсолютным значением. Произвольный кватернион можно записать по аналогии с экспоненциальной формой комплексного числа: ( ), в этом случае .

Теперь становится понятен смысл сопряженного кватерниона: что, как и в случае комплексных чисел, соответствует повороту в противоположном направлении на соответствующий угол.

Заметим еще одно удобное свойство кватерниона: . Для единичных кватернионов, которыми мы, собственно, и будем пользоваться: .

На самом деле, для поворотов нам нужен кватернион с половинным углом: .

Теперь давайте посмотрим, как такой кватернион поворачивает вектор.

Мы хотим повернуть при помощи кватерниона вектор (получим вектор ), который мы решили представлять кватернионом с произвольной скалярной частью . Разобьем вектор на два слагаемых: , первое из которых коллинеарно : , а второе - перпендикулярно: . Соберем из них новые кватернионы, скалярную часть отнесем к параллельной части: . Преобразуем их по отдельности: . Из геометрических соображений понятно, что измениться должна только перпендикулярная часть: , ее вращение произойдет в плоскости на угол (рисунок 2.5).

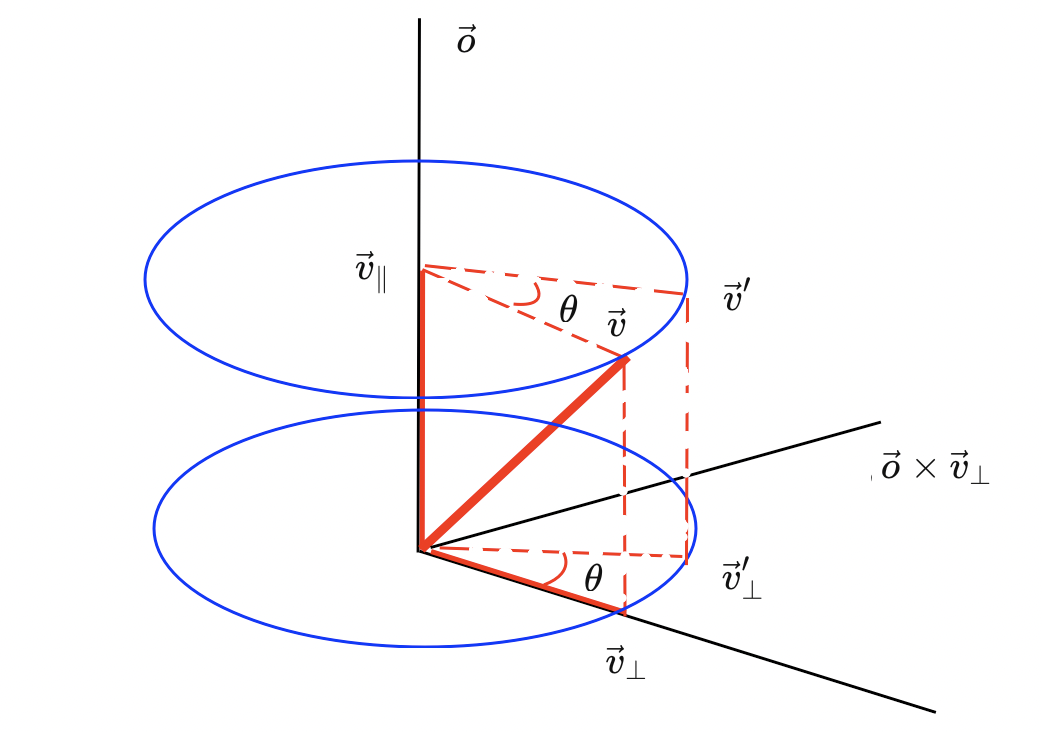
Давайте применим поворот к :

Заметим, что , приведем подобные слагаемые и получим:

Ура! Параллельная часть вектора и скаляр не изменились - есть шанс на то, что этот кватернион действительно описывает нужный нам поворот :) Посмотрим теперь на ортогональную часть вектора:

Теперь вспомним, что , а также вспомним про тригонометрические формулы двойного угла и про раскрытие двойного векторного произведения по формуле Лагранжа ("бац минус цаб"):

,

что в нашем случае дает:

Что как раз и соответствует повороту в плоскости на угол !

Таким образом получается, что кватернион, осуществляющий поворот вокруг оси на угол мы находим как . Так же верно и обратное: .

Тут - это "половинный" кватернион.

Значения угла и компонент оси можно найти из компонент кватерниона :

, (можно испольовать любую компоненту векторной части).

Если , то тогда ось может быть выбрана произвольно, а угол аоврота равен 0, то есть сам вектор поворота . Ну и , что мы и получили в кватернионном виде.

Но надо иметь ввиду, что если мы угол "перекрутили" за полный оборот, то кватернион нам покажет только остаток от полного оборота.

2.7 С точки зрения алгебры

Геометрический подход нагляден. Но мне больше нравится своей лаконичностью. Хотя, тут трудно провести четкую границу. Предлагаю просто рассмотреть еще один подход у описанию вращения.

Рассмотрим неполный кватернион без скалярной части , причем . Теперь найдем . Получается, что этот кватернион работает как мнимая единица. А так как мы рассмотрели произвольный вектор с единичной длиной, то можем сделать вывод, что любой произвольный единичный вектор на мнимых осях может рассматриваться как мнимая единица.

Рассмотрим два ортогональных единичных вектора и , причем, будем полагать, что и . Тогда можем ввести третий вектор . По свойствам векторного произведения можем записать: , , , , . Что соответствует взаимопревращениям мнимых единиц, а скалярные квадраты каждого из этих векторов в кватернионной представлении равны -1.

Значит мы можем ввести альтернативный базис - который функционирует абсолютно аналогично обычным мнимым единицам.

Теперь, имея ось вращения и угол мы можем ввести базис мнимых единиц, одна из которых, например соответствует . Тогда поворот будет представлять из себя кватернион . Вращаемый вектор представим в том же базисе в виде кватерниона с произвольной скалярной частью: .

А вращение этого кватерниона будет осуществляться как поворот вокруг одной оси: . А этот механизм нам уже знаком. Не так очевидно, как в геометрической интерпретации, за то лаконичнее :)

2.8 Интерполяция поворотов

Ну, и, собственно, основное преимущество кватернионов: способность превращать сферическую линейную интерполяцию поворотов в линейную интерполяцию векторов.

Прежде, чем говорить об интерполяции поворотов, давайте разберем постановку задачи сферической линейной интерполяции. Пусть у нас есть две точки, заданные в виде радиус-векторови, тогда отрезок между этими точками мы можем описать параметром : . При изменении параметра от до , Мы будем получать точки отрезка , делящие отрезок на две части, пропорционально . При , результат интерполяции будет совпадать с , а при - c (рисунок 2.6).

Но если предположить, что точкиилежат на поверхности сферы с центром в начале координат . Если нам нужно при интерполяции получить плоскую дугу, составляющую участок окружности, которая получается при пересечении сферы с плоскостью вращения, заключенной между точкамии, то линейная интерполяция нам не подходит. Вместо линейной интерполяции нам нужно использовать линейную сферическую интерполяцию. Линейная сферическая интерполяцию описывает участок дуги параметром , пропорционально которому будет разбиваться угол дуги между точками и, в отличие от линейной интерполяции:

, где угол между векторами и .

При , результат интерполяции будет совпадать с , а при - c (рисунок 2.6) .

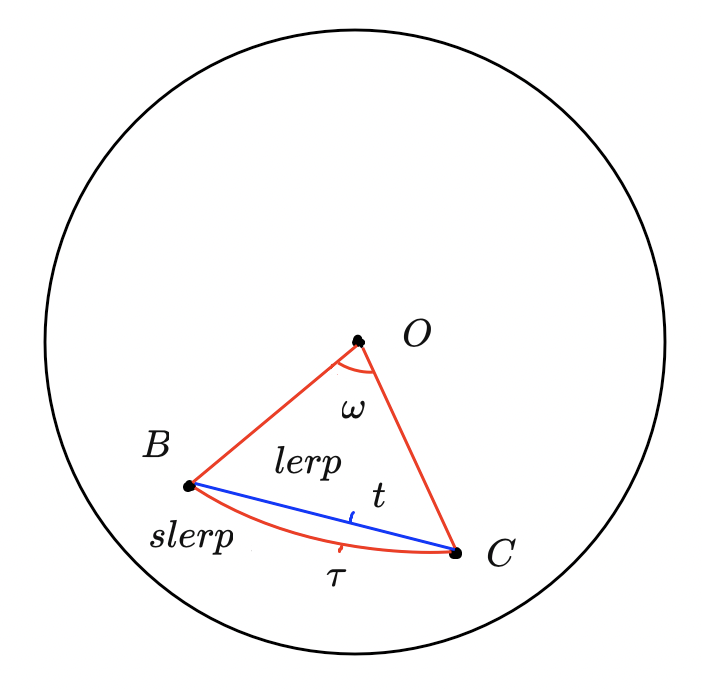
Теперь представим ситуацию, когда нам известны кватернионы поворота объектаи в два момента времени и . То есть, каждый вектор, который в начальный момент времени выглядел как , в момент времени будет иметь значение , а в момент времени будет иметь значение Для реализации плавного изменения ориентации объекта, нам необходимо построить модель интерполяции между и . Давайте рассмотрим такие сточки, и , чтобы первый поворот превращал в , а второй превращал в . Теперь задачу интерполяции поворотов, описываемыхи можно свести к построению сферической линейной интерполяции между точками и - равномерно двигаться по углу дуги между этими точками.

Какой кватернион реализует преобразование из ориентации в момент времени в ориентацию в момент времени ? Это кватернион, отменяющий и вводящий в действие : . У него, как и полагается любому кватерниону, есть соответствующая ось вращения и угол , который нам и нужно поделить на на части пропорционально параметру интерполяции . То есть, нам нужно реализовать повороты на углы .

Но мы же помним, что множителю при значении угла соответствует показатель степени кватерниона: . Соответственно, интерполяция поворотов между и сводится к следующему выражению: . Очевидно, что при и итоговая конструкция будет совпадать с и соответственно.

Для расчёта степеней кватернионов достаточно найти соответствующие углы и оси и собрать новые кватернионы с аналогичной осью и модифицированным углом. Но это удобно, если повороты изначально заданы в виде кватернионов. Если же повороты изначально заданы осями , и углами и соответственно, то для интерполяции поворотов удобнее использовать другую формулу. Попробуем степени выразить через экспоненту и логарифмы:

Ну, а логарифм кватерниона, как мы помним, это вектор поворота. Соответственно, интерполяция сводится к следующему виду: , что соответствует обычной линейной интерполяции вектора поворота.

Заключение

Я постарался изложить теорию последовательно и без "черных ящиков". Надеюсь, у тех, кто осилил дочитать досюда, осталось меньше пробелов в понимании кватернионов и их применения для вращений в трехмерном пространстве.

На самом деле, кватернионы это только один компонент более продвинутой системы - бикватернионов. Но для тех, кто понял кватернионы, у меня есть хорошая новость: переход от кватернионов к бикватернионам проще, чем переход от комплексных чисел к кватернионам. А возможности бикватернионов богаче. Они могут описывать не только повороты вокруг начала координат, но еще параллельный перенос и поворот вокруг произвольного центра - то есть, все виды движения в 3D.

Вот в следующей публикации и поговорим о бикватернионах :)