Автор статьи: Виктория Ляликова

Привет Хабр! В этой статье мы рассмотрим такое понятие в машинном обучении, как компромисс смещения и дисперсии (bias-variance Tradeoff). Так как понимание того, что можно изменить в процессе обучения нашего алгоритма обучения, приведет нас к созданию более точных моделей.

Введение

Основная цель машинного обучения состоит в том, чтобы модель училась на предоставляемых ей данных и генерировала прогнозы на основе закономерностей, наблюдаемых в процессе обучения. Однако это еще не все. Полученную модель необходимо постоянно совершенствовать в зависимости от результатов, которые она генерирует. Также мы оцениваем производительность модели с помощью таких показателей, как точность, среднеквадратическая ошибка, показатель F1 и т.д. и пытаемся их улучшить. И если мы хотим получить достаточно гибкую модель без ущерба ее корректности, то настройка производительности модели может оказаться достаточно непростой задачей.

В модели машинного обучения с учителем мы обучаемся на входных данных (X) таким образом, чтобы прогнозируемые значения (Y) были как можно ближе к фактическим значениям. И разница между фактическими значениями и прогнозируемыми является ошибкой и используется для оценки производительности модели. Ошибка любого контролируемого алгоритма машинного обучения состоит из ошибки смещения (bias), ошибки отклонения(дисперсии) и шума. При этом шум является неустранимой ошибкой, которую нельзя никак контролировать независимо от того, какой бы алгоритм не использовался. Шум может быть вызван такими факторами как неизвестные переменные, которые влияют на отображение входных данных в выходные. И получается, что наша задача заключается в том, чтобы контролировать ошибки смещения и дисперсии и пытаться их минимизировать в максимально возможной степени.

В самых простых терминах, смещение - это разница между прогнозируемым и ожидаемым значениями. Дисперсия говорит о разбросе наших данных. Проиллюстрируем визуально компромисс смещения и дисперсии на диаграмме “яблочко”. Красный круг в центре области — это модель, которая идеально предсказывает правильные значения. Одна синяя точка соответствует реализации нашей модели, обученной на некоторой обучающей выборке, а всего синих точек столько, сколько было обучающих выборок. 

Во время обучения модель делает определенные предположения на тех данных, которые ей предоставили. И когда далее эти предположения вводятся в данные для тестирования, то они не всегда могут быть верными. И иногда мы получаем хорошее распределение обучающих данных, поэтому мы прогнозируем очень хорошо и находимся близко к цели, тогда как иногда наши обучающие данные могут быть полны выбросов или нестандартных значений, что приводит к ухудшению прогнозов. Эти разные реализации приводят к разбросу попаданий в цель. Большое смещение соответствует тому, что модели в среднем не попадают в цель, а при большом разбросе модели могут делать как точные предсказания, так и довольно сильно ошибаться.

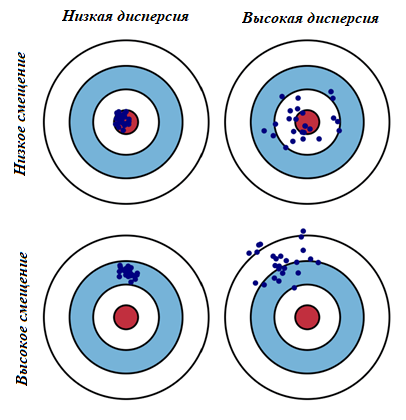
Высокая дисперсия может возникать из-за недостаточного количества данных для обучения модели. Когда обучающая выборка маленькая, модель может подстраиваться под шум в данных и проявлять высокую чувствительность к конкретным примерам, вместо обобщения общих закономерностей.

Причиной смещений может являться неправильный сбор данных в датасете, то есть не учтены все характеристики. Например, мы отбираем в выборку только схожие между собой данные, то есть фактически рисуем мишень вокруг места, куда попадем. Также причинами могут быть неправильное формирование тренировочного набора из датасета или неправильное измерение ошибок.

Обычно, алгоритмы нелинейного машинного обучения часто имеют высокую ошибку смещения, но низкую дисперсию. А алгоритмы нелинейного машинного обучения часто имеют низкое смещение, но большую дисперсию.

Вывод разложения смещения-дисперсии (bias-variance) для MSE

Рассмотрим задачу с математической точки зрения. Пусть X - входные данные, состоящие из набора точек x_1,x_2,..,x_n, Y = (y_1,y_2,...,y_n) - целевая переменная. Мы предполагаем, что существует функция f(x), такая что y=f(x)+e.

Здесь e - это какой-то шум, который имеет нулевое среднее ₍) значение и дисперсию .

Цель нашей модели - предсказать значения, как можно близкие к f(x) с помощью некоторого алгоритма обучения.

Мы хотим добиться как можно лучшей точности, измеряя среднеквадратическую ошибку MSE между y и . Функция потерь на одной тестовой точке х в зависимости от реализаций Х и e равна

Наше требование заключается в том, чтобы было минимальным как для точек x_1,x_2,..,x_n, так и для точек за пределами нашей выборки. Конечно сделать это идеальным невозможно, поскольку у содержит шум e. Найти можно с помощью любого контролируемого алгоритма обучения. Причем независимо от того, какую мы бы ни выбрали, ее можно разложить на ожидаемую ошибку. Ожидаемая ошибка - это фактически наиболее ожидаемое значение (ошибку которую мы ожидаем), которое является обобщением средневзвешенного значения. В теории вероятностей наиболее ожидаемым значением является математическое ожидание, которое в российской литературе обозначается буквой M, а в иностранной литературе буквой E(expected value). Здесь и далее дисперсию буду обозначать буквой D.

где

Можно обозначить

Вывод разложения ошибки является достаточно несложным, достаточно помнить свойства математического ожидания и формулу дисперсии.

Далее достаточно разложить каждый член в этой сумме

1. Найдем

Помним, что есть вот такая формула для дисперсии

, тогда получаем

2. Найдем и при этом помним, что математическое ожидание является линейной функцией,  не зависит от данных, а ошибка имеет и

3. Найдем

Теперь подставляем все в наш предыдущий вывод Err

То есть .

- это неустранимая ошибка измерения.

Дисперсия показывает насколько изменится наш классификатор, если мы будем обучаться на другом обучающем наборе и говорит нам о разбросе наших  данных. Модель с высокой дисперсией уделяет много внимания обучающим данным и не обобщает данные, которые она раньше не видела. В результате такие модели очень хорошо работают на обучающих данных, но имею высокий уровень ошибок на тестовых данных.

Смещение - это разница между средним предсказанием нашей модели и правильным значением, которое мы пытаемся предсказать. В нашем случае предсказание нашей модели - это , а предсказать пытаемся . Модель с высоким смещением уделяет мало внимания обучающим данным и чрезмерно упрощает модель. Это всегда приводит к высокой ошибке в обучающих и тестовых данных.

Пример расчета оценок смещения и дисперсии

Попробуем вычислить разложение на смещение и разброс на каком-нибудь практическом примере. Возьмем набор данных о диабете индейцев пима и сформируем на его основе задачу классификации. Сначала посмотрим на набор данных, оценим его и поэкспериментируем на алгоритмах “случайных лес” и “дерево решений”.

import pandas as pd
import numpy as np
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
from sklearn.utils import resample
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
df = pd.read_csv('D:/vika/datasets/diabetes.csv')
df.describe()

В этом наборе данных в столбцах Glucose, BloodPressure, SkinThickness, Insulin, BMI имеются нулевые значения. Скорее всего это пропущенные значения, которые были заменены нулями. Сначала заменим нули на значения np.nan, а затем восстановим их с помощью метода IterativeImputer() из библиотеки sklearn. 

new_data = df.copy(deep=True)
colsFix = ['Glucose', 'BloodPressure', 'SkinThickness', 'Insulin', 'BMI']
new_data [colsFix] = new_data[colsFix].replace(0, np.NaN)
# определяем импортер
myImputer=IterativeImputer()
# устанавливаем imputer на X
myImputer.fit(new_data)
#получаем восстановленные данные
myImputer_data = myImputer.transform(new_data)
# полученные данные преобразовываем в DataFrame
myImputer_data = pd.DataFrame(myImputer_data,columns = new_data.columns)

Проверим сбалансированность данных

df.groupby('Outcome').count()

Данные являются несбалансированными, поэтому с помощью метода resample() из библиотеки sklearn семплируем выборку.

data_major = myImputer_data [(myImputer_data['Outcome']==0)]
data_minor = myImputer_data [(myImputer_data['Outcome']==1)]
upsample = resample(data_minor, replace = True, n_samples = 500, random_state = 42)
clean_data = pd.concat([upsample, data_major])

Далее определим матрицу признаков и целевой вектор и нормализуем данные

X = clean_data.drop(['Outcome'],axis=1)
y= clean_data.Outcome
sc=StandardScaler()
standart_X = pd.DataFrame(data = sc.fit_transform(X), index = X.index, columns = X.columns)
x_train, x_test, y_train, y_test = train_test_split(standart_X, y, test_size = 0.2, random_state = 0)

Для решения задачи классификации сначала возьмем алгоритм “случайный лес” RandomForestClassifier(). В этом алгоритме попробуем изменять параметр n_estimators, который отвечает за количество деревьев в ансамбле и будем рассчитывать различные значения смещения и дисперсии в зависимости от этого параметра. А вычислять значения смещения и дисперсии будем с помощью интересного метода bias_variance_decomp() из библиотеки mlextend.

from sklearn.ensemble import RandomForestClassifier
avg_forest = []
bias_forest = []
var_forest = []
k_forest = []
for k in range(1, 31):
	k_forest.append(k)
	clf_forest = RandomForestClassifier(n_estimators = k)
	clf_forest.fit(x_train, y_train)
	avg_expected_loss, avg_bias, avg_var = bias_variance_decomp(
	clf_forest, x_train.values, y_train.values, x_test.values, y_test.values, loss='mse', num_rounds=50)
	avg_forest.append(avg_expected_loss)
	bias_forest.append(avg_bias)
	var_forest.append(avg_var)

Теперь у нас есть 3 массива со средними значениями потерь, средними значениями смещения и средними значение дисперсии для каждого алгоритма случайного леса в зависимости от параметра n_estimators. И посмотрим на графике на полученную зависимость.

import matplotlib.pyplot as plt
%matplotlib inline
plt.figure(figsize=(10,5))
plt.xlabel('Different Values of K')
plt.ylabel('Tradeoff bias-variance RandomForest')
plt.plot(k_forest, bias_forest, color = 'r', label = "avg_bias")
plt.plot(k_forest, var_forest, color = 'b', label = 'avg_var')
plt.plot(k_forest, avg_forest, color = 'g', label = 'avg_tree')
plt.legend(bbox_to_anchor=(1, 1),
       	bbox_transform=plt.gcf().transFigure)
plt.show()

Получается, что с увеличением параметра n_estimators смещение почти не изменяется (немного возрастает), зато дисперсия падает, а также падает среднее значение потерь. Таким образом с увеличением количества деревьев мы получаем более сложную модель, что дает низкое смещение, но чувствительность к шуму и колебаниям в новых данных, поэтому такие предсказания дают разброс.

А теперь проведем такой же эксперимент с алгоритм DecisionTree и получим следующую картину.

Видим, что здесь дисперсия слегка возрастает, зато падает смещение и среднее значение потерь. Известно, что деревья малой глубины будут в большинстве случаев имеют высокое смещение и низкий разброс предсказаний, так как они не могут слишком хорошо запомнить обучающую выборку. А глубокие деревья, наоборот, могут безошибочно выучить обучающую выборку и потом будут иметь высокий разброс в зависимости от выборки, однако их предсказания будут в среднем точнее.

Компромисс смещения дисперсии

Любая модель машинного обучения должна стремиться к низкой дисперсии и низкому смещению. Так как высокое смещение приводит к недообучению модели (модель недооценивает или переоценивает какой-либо параметр), а высокая дисперсия приводит к переоснащению (переобучению) модели, то есть насколько сильно разбросаны значения. Но на практике получается, что модели с высоким смещением, как правило имеют низкую дисперсию, а  модели с низким смещением как правило имеют высокую дисперсию.

Компромисс между смещением и дисперсией относится к компромиссу, который имеет место, когда мы решаем снизить смещение, что обычно увеличивает дисперсию, или уменьшить дисперсию, что обычно увеличивает смещение. А на практике нас интересует только минимизация общей ошибки модели, и для этого как раз необходимо найти правильный баланс между дисперсией и смещением.

Нам нужна модель, которая достаточно сложна, чтобы фиксировать истинную связь между независимыми переменными и переменной отклика, но не слишком сложна, чтобы находить шаблоны, которых на самом деле не существует.

Когда модель сложна она подгоняет данные. Это происходит потому, что слишком сложно найти закономерности в обучающих данных, которые просто вызваны случайностью. Этот тип модели вероятно будет плохо работать с невидимыми данными.

Но когда модель слишком проста, она не соответствует данным. Это происходит потому, что предполагается, что истинная связь между объясняющими переменными и переменной отклика более проста, чем она есть на самом деле.

В различных интернет-ресурсах часто можно встретить следующее изображение.

Оно как раз иллюстрирует компромисс смещения и дисперсии (bias-variance tradeoff). По мере увеличения сложности модели общая ошибка уменьшается, но только до определенного момента. После определенного момента дисперсия начинает увеличиваться, и общая ошибка тоже увеличивается. Этот график призван показать, что существует оптимальная сложность модели при которой баланс между переобучением и недообучением достигается с минимальной ошибкой.

Здесь важно понимать, что независимо от того, насколько хорошо мы создадим нашу модель, наши данные будут иметь определенное количество шума или неустранимую ошибку.

Подходы к устранению смещения и дисперсии.

Если построенная модель имеет большое смещение, то можно попробовать следующие подходы:

• Увеличение размеров модели. Например для нейронной сети это может быть увеличение количества нейронов и слоев в сети, для деревьев - увеличение глубины дерева. Если при этом получится, что увеличивается дисперсия, можно попробовать использовать регуляризацию, которая может помочь устранить увеличение разброса.

• Модифицирование входящих признаков, исходя из анализа ошибок. Например можно создать дополнительные признаки. Такие признаки могут помочь справиться как со смещением, так и с разбросом.

• Модификация архитектуры модели (например архитектуры нейронной сети), чтобы она больше подходила для задачи.

• Уменьшение или отказ от регуляризации

Если построенная модель имеет высокую дисперсию, то можно попробовать следующие подходы:

• Увеличение размера обучающей выборки. Это самый простой и наиболее реальный путь к уменьшению дисперсии. Он работает до тех пор, пока есть возможность существенно увеличивать количество используемых данных и имеются вычислительные мощности для их обработки.

• Добавление ранней остановки (например остановить градиентный спуск раньше, базируясь на значении ошибки на валидационной выборке). Такая техника уменьшает разброс, но увеличивает смещение.

• Отбор признаков для уменьшения количества/типов входящих признаков (вручную или через алгоритм, кроме того вводить наказание за новые признаки). Этот подход может помочь с проблемой разброса, но также может увеличить смещение. Также имеется одна опасность - выбросить нужные признаки. Также, если обучающая выборка маленькая, то отбор признаков может оказаться очень полезным.

• Уменьшение размера (сложности) модели (например количество нейронов.слоев). Данный подход надо использовать с осторожностью. Преимуществом такого подхода служит ускорение процесса обучения модели за счет уменьшения потребности в вычислительных мощностях.

• Использование регуляризации позволяет снижать параметр (вес, коэффициент) признака и, таким образом, снижать его значимость.

На практике наиболее распространенным способом минимизации тестовой ошибки является использование перекрестной проверки или кросс-валидации. Такой метод поможет сравнить между собой несколько моделей и выбрать наилучшую для конкретной задачи.

В заключении хочется сказать, что дилемма смещения и дисперсии встречается не только в статистике и машинном обучении, но и в обучении людей. В одном исследовании утверждается, что люди используют такую эвристику как “высокое смещение+низкая дисперсия”, то есть мы заблуждаемся, зато очень уверенно!

Что же касается машинного обучения, напоминаю о том, что у моих коллег из OTUS есть большая линейка курсов от практикующих экспертов. Подробнее узнать про курсы можно тут, а в календаре мероприятий вы можете зарегистрироваться на интересующие вас бесплатные уроки.