Развитие генеративных моделей ИИ продвигается семимильными шагами и будурожит сознания миллионов людей во всем мире. Все больше скандалов, интриг и расследований связаны с ними, мы становимся свидетелями действительно революционного прорыва технологий в этой сфере. Однако сегодня именно модель PFGM ++ станет объектом нашего внимания, потому что она в 10-20 раз быстрее знакомых всем диффузионных моделей справляется с задачами генерации изображений при сопоставимой производительности.

Важно отметить, что основоположницей модели PFGM ++ (генеративной модели потока Пуассона ++) 2023 года стала модель PFGM, представленная годом ранее, поэтому ссылаться мы будем на нее.

На данном этапе уже можно сделать выводы, что работать мы будем со следующими физическими законами:

1. диффузией, непосредственно лежащей в основе стандартных генеративных  моделей;

2. полем Пуассона, ставшим ключевым явлением в создании новых технологий.

Если рассматривать генеративные модели ИИ со стороны физики, то диффузионные основываются на термодинамике, беря за основу то, что, например, любое локализованное распределение газа в конечном итоге равномерно заполнит все пространство просто за счет случайного движения (непосредственно явление диффузии).

Таким образом, формулируется постулат – случайное начальное распределение преобразуется в равномерное распределение с течением времени. Исходя из этого, диффузионные модели искажают изображения случайным шумом.

Тут пиксели рассматриваются как локализованное облако частиц, которые со временем "рассеиваются" в тот самый случайный шум (который, на самом деле, называется гауссовским).

В данном случае основной целью машинного обучения становится возможность вернуться к начальной точке (или к чему-то максимально похожему), обращая вспять этот процесс искажения.

Следовательно, открывается возможность генерировать данные, просто делая выборку из гауссовского распределения и применяя изученное преобразование.

Генеративные модели пуассоновского потока в свою очередь  основываются на электростатике. Тут же центральная идея заключается в том, что любое распределение электронов в гиперплоскости  генерирует электрическое поле, которое преобразует распределение в равномерное угловое, в соответствии с динамикой, определяемой полем.

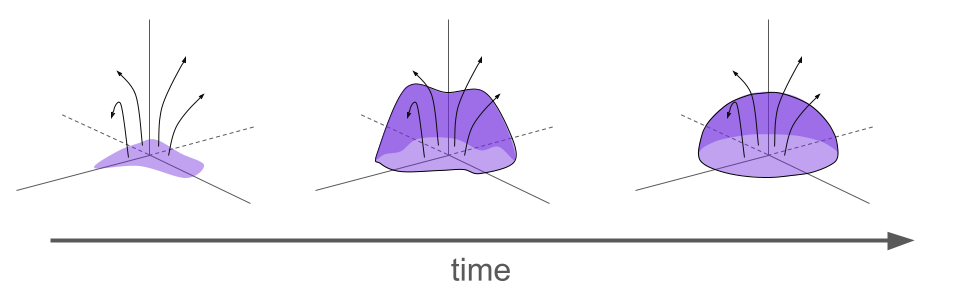
Таким образом, если нам известно электрическое поле (оно же поле Пуассона), создаваемое данным распределением, то мы можем начать с точек, равномерно отобранных на полусфере, и запустить динамику вспять, чтобы восстановить исходное, начальное распределение.

Далее, хочу подробнее рассмотреть этот принцип работы PFGM со стороны физической модели (эта часть может показаться чрезмерно перегруженной для пользователей, в меньшей степени заинтересованных в физике генеративных моделей ИИ, поэтому можно сразу перейти к части “генерация изображений с помощью PFGM”)

Генеративные модели пуассоновского потока – подробный обзор

Рассмотрим электрическое поле, генерируемое произвольным распределением заряда. Очень близко к распределению электрическое поле будет достаточно сложным и, в общем случае, иметь большую кривизну.

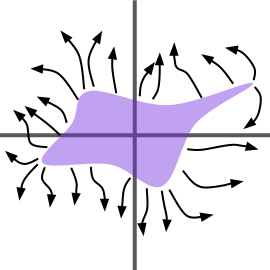
Однако на очень большом расстоянии d от распределения заряда поле гораздо проще. Это означает, что можно считать, что распределение заряда "сворачивается" до определенной точки, концентрируя весь свой заряд в ней. Электрическое поле для точечного заряда довольно простое - оно имеет радиальное направление и величину, обратно пропорциональную квадрату расстояния от точки:

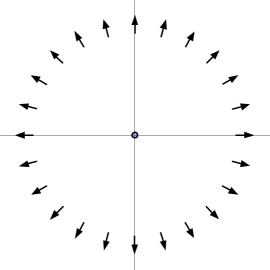
Учитывая, что на очень большом расстоянии электрическое поле радиально, поверхность, касательная к полю, на этом расстоянии сферическая.

При этом, авторы PFGM доказывают, что эта поверхность не только сферическая, но и ее плотность потока равномерна. Ниже мы видим распределение заряда в форме сердца в плоскости z = 0 вместе с линиями электрического поля (черные стрелки), которые оно генерирует. Плотность потока через окружающую полусферическую поверхность (почти) равномерна.

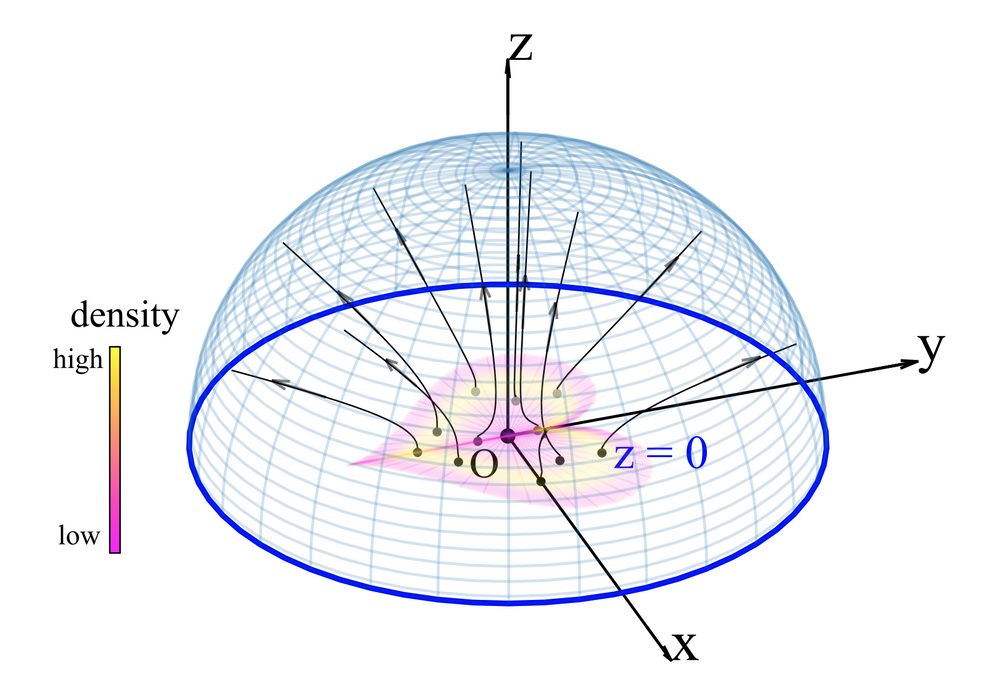
Если мы рассмотрим поле Пуассона в многомерном пространстве, например, для распределения данных изображения, то мы можем просто равномерно отбирать точки из многомерной полусферы и запускать динамику в обратном времени для генерации изображений из распределения данных:

Изучение поля Пуассона

Смоделируем динамику частиц под влиянием поля Пуассона, генерируемого распределением данных.

1. Дополнение данных

Важно отметить, что распределение данных лежит в двумерной плоскости, но отображается на трехмерную полусферу. Это верно в общем случае для всех PFGM моделей - N-мерные данные дополняются измерением z и помещаются в гиперплоскость z= 0 нового (N+1)-мерного пространства. Затем данные отображаются в (N+1)-мерную полусферу.

Причина этого пространственного увеличения заключается в необходимости недопущения “коллапса режима”. Ниже мы видим (отрицательное) Поле Пуассона, генерируемое однородным диском в плоскости XY. Процесс выборки заключается в случайном отборе точек в пространстве и следовании по полю до места распределения данных. Как мы видим, все траектории сходятся к началу координат, а это значит, что наша модель будет генерировать изображения, которые не имеют разнообразия и, следовательно, страдают от коллапса режимов.

Добавление к данным дополнительного измерения позволяет обойти эту проблему. Ниже мы видим тот же двумерный однородный диск сверху, теперь в плоскости XY с добавленной размерностью Z.

Хотя, по сути, у нас все еще есть двумерное распределение данных, теперь оно встроено в трехмерное пространство, таким образом генерируя 3-мерное поле Пуассона. Если мы теперь выберем точки в этом трехмерном пространстве, например, из плоскости YZ, и проследим их траектории через поле до XY, нам будет предоставлен ряд новых траекторий, которые больше не сворачивают к началу координат, а вместо этого пересекают разные точки в распределении данных. То есть, наша модель больше не страдает от коллапса режимов.

2. Вычисление эмпирического поля

Для выборки с помощью модели PFGM мы должны знать поле Пуассона. Чтобы изучить поле Пуассона, нам нужно было бы точно знать распределение данных, но распределение данных - это то, из чего мы стремимся сделать выборку. Если бы мы уже изначально знали аналитическую форму распределения, нас бы не волновало пуассоновское поле, которое оно генерирует.

Вместо того чтобы пытаться изучить точное поле Пуассона, мы будем рассматривать эмпирическое поле, которое генерируется обучающими данными, рассматриваемыми как точечные заряды.

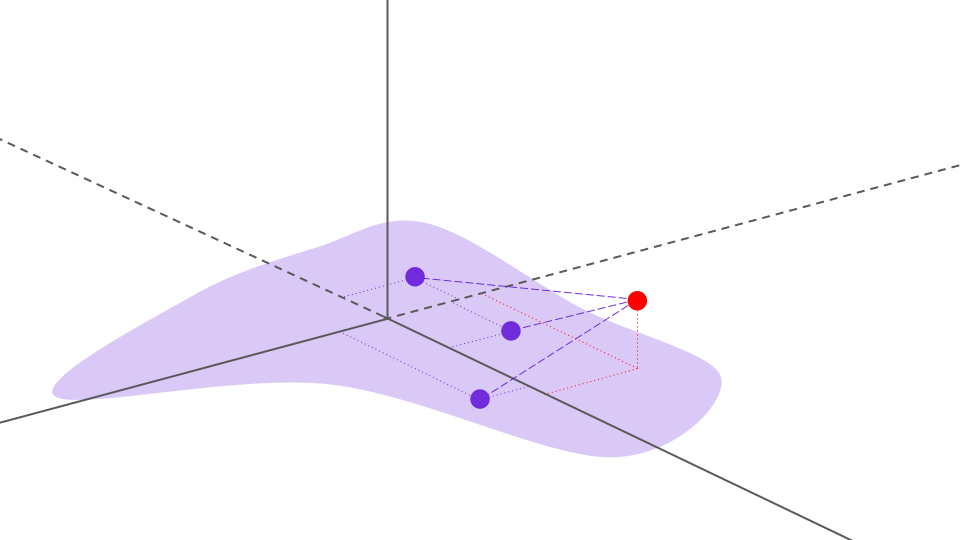
Выше приведен пример распределения (светло-фиолетовый), для которого мы стремимся сгенерировать данные, а также несколько точек данных, выбранных из этого распределения (фиолетовые точки). Кроме того, существует случайно выбранная точка в пространстве (красная точка), в которой мы стремимся оценить поле Пуассона (или, что эквивалентно, вычислить эмпирическое поле).

Чтобы вычислить эмпирическое электрическое поле, мы суммируем поля, генерируемые каждым точечным зарядом, что эквивалентно полному эмпирическому полю в этой точке благодаря принципу суперпозиции. Вклад поля каждой отдельной точки данных можно увидеть ниже в виде фиолетовой стрелки, а чистое поле представлено красной стрелкой.

*Согласно принципу суперпозиции, электрическое поле, создаваемое системой зарядов, равно векторной сумме электрических полей, создаваемых каждым отдельным зарядом в отсутствие остальных.

Мы вычисляем эмпирическое поле для многих случайно выбранных точек в пространстве, отдавая предпочтение близким к точкам данных, поскольку кривизна поля будет более значительной в этих областях, поэтому для достаточной аппроксимации требуется большее разрешение.

3. Вычисление потери и обновление аппроксиматора функции

Для выполнения выборки с помощью PFGM нам требуется непрерывное аналитическое представление пуассоновского поля, а не значения только в дискретных точках, подобные тем, которые мы рассмотрели  выше. Поэтому мы должны построить аппроксиматор функции для эмпирического поля в этих точках.

Как должен выглядеть этот аппроксиматор?

Аппроксиматор функции должен принимать N + 1-мерный вектор, представляющий точку в нашем расширенном пространстве, и возвращать N + 1-мерный вектор, представляющий эмпирическое поле в этой точке. Наилучшим выбором для такого отображения является архитектура U-Net, которую и реализуют авторы PFGM.

Таким образом, U-Net (блок-схема) принимает точку в пространстве (синий вектор) и возвращает приблизительное эмпирическое поле в этой точке (красный вектор), сгенерированное точками данных, выбранными из распределения данных / зарядов (фиолетовый).

Чтобы обучить U-Net, мы просто вычисляем средние потери L2, а затем обучаем с помощью оптимизатора на основе градиента, такого как Adam. Вот и все!

Выборка с помощью PFGM

Повторю, что траектории пуассоновского поля представляют собой биекцию (взаимно однозначное отображение одного множество в другое) между распределением данных и равномерной полусферой. Поэтому, чтобы выбрать точки из распределения данных, мы выбираем их из равномерного углового распределения, а затем заставляем двигаться в обратном направлении вдоль поля Пуассона, пока не достигнем гиперплоскости z=0. Соответствующее дифференциальное уравнение имеет вид:

В соответствии с данным уравнением, в каждый момент времени точка должна смещаться в направлении отрицательного поля Пуассона (следовательно, соответствующим решением будет траектория, которая прослеживается в обратном направлении вдоль этого поля до гиперплоскости z=0)

На практике для генерации данных с использованием генеративной модели поля Пуассона мы должны:

1. осуществляем равномерную выборку данных (точек) на полусфере;

2. прибегаем к решению ОДУ для перемещения точек в обратном направлении вдоль поля Пуассона;

3. двигаемся в обратном направлении до тех пор, пока не достигнем гиперплоскости z = 0, после чего мы сгенерируем новые данные из обучающего распределения.

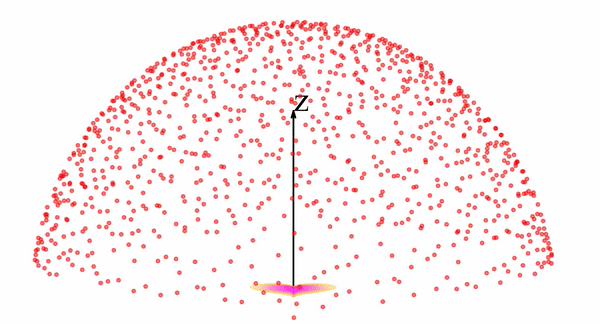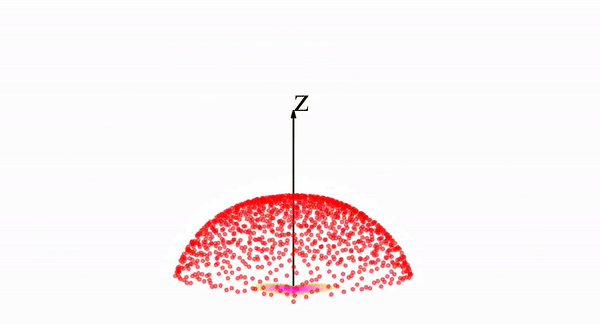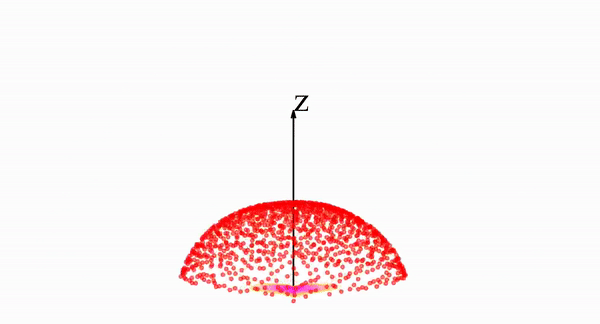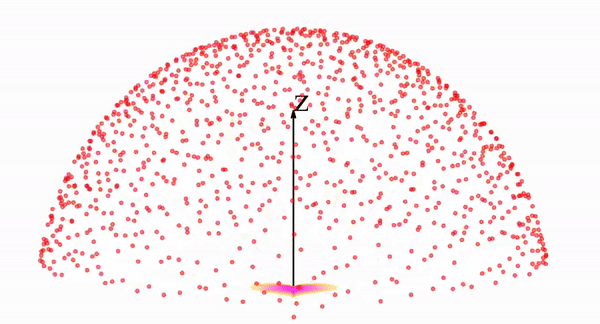
В визуальном пространстве обратная эволюция в процессе выборки выглядит следующим образом:

https://www.assemblyai.com/blog/content/images/2022/10/celeba_movie_50.gif

Генерация изображений с помощью PFGM

Рассмотрим основные шаги и части непосредственного процесса генерации изображений, предоставленные авторами PFGM в Google Colab.

1. Смена аппаратного ускорителя на GPU

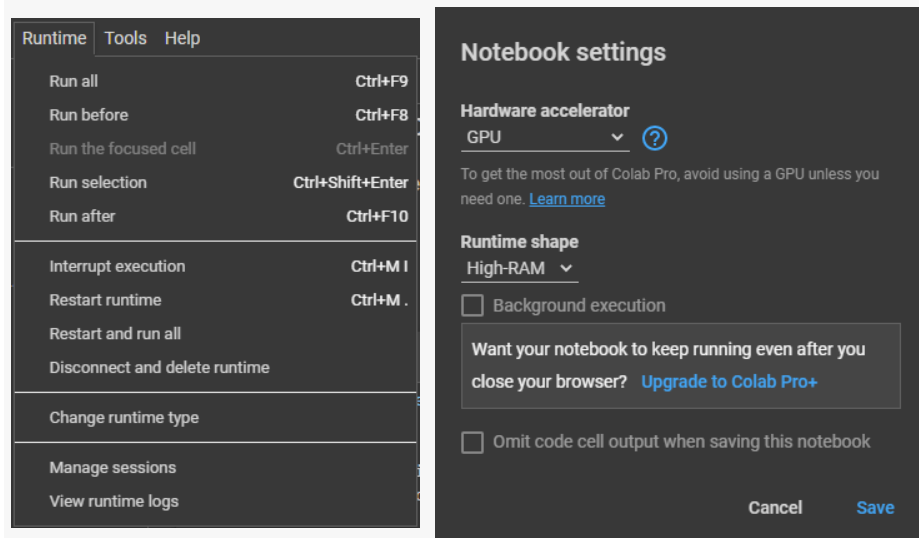
2. Настройка среды

Скачайте репозиторий PFGM с помощью следующей команды: https://github.com/Newbeeer/Poisson_flow.git

Затем перейдите в репозиторий:

import os

os.chdir("Poisson_flow")

Выполните следующую команду, чтобы изменить файл requirements.txt для корректной работы в Colab:

with open("requirements.txt", "r") as f:
    new_reqs = ''.join(f.readlines()[1:])
    new_reqs = new_reqs.replace("numpy==", "numpy==1.21.6")
    new_reqs = new_reqs.replace("pandas==1.4.2", "pandas==1.3.5")
    new_reqs = new_reqs.replace("torch==1.12.1+cu116\ntorchvision==0.13.1+cu116\n", "")


with open("requirements.txt", "w") as f:
    f.write(new_reqs)

Теперь установите необходимые требования с помощью следующей команды:

!pip install -r requirements.txt

На этом этапе вам придется перезапустить программную среду и установить оставшиеся требования:

!pip install torch --pre --extra-index-url https://download.pytorch.org/whl/nightly/cu116

!pip install Ninja

!pip install gdown

!pip uninstall jax

!pip install jax==0.3.22

3. Создание изображений

Убедитесь, что вы перезапустили программную среду (Runtime > Restart runtime).

Перейдите в каталог PFGM:

import os

os.chdir("Poisson_flow")

rootdir = os.getcwd()  # Save root directory for later

Импортируйте изображение для отображения картинки:

from IPython.display import Image

Далее для генерации введите следующее:

!python3 main.py --config ./configs/poisson/cifar10_ddpmpp.py \

--mode eval

--workdir cifar10_ddpmpp \

--config.eval.enable_sampling \

--config.eval.save_images \

--config.eval.batch_size 100

И после ввода Image('cifar10_ddpmpp/eval/ode_images_10.png')выводится изображение:

А более подробно все процессы можно рассмотреть здесь.

Результаты

1. PFGM достигает лучших показателей Inception score (9,68) и FID score (2,35) среди нормализующих моделей потока для CIFAR-10.

2. PFGM работают в 10-20 раз быстрее, чем SDE-методы, использующие аналогичную архитектуру, при сохранении сопоставимого качества выборки.

3. Обратное ОДУ в случае PFGM позволяет использовать множество различных архитектур.

4. PFGM демонстрируют масштабируемость для создания изображений с более высоким разрешением.

PFGM ++

Вернемся к идее о создании (N+1)-мерного пространства для дальнейшего отображения точек в (N+1)-мерную полусферу (в моделях PFGM).

Модель PFGM++ также предполагает создание (N+D)-мерного пространства. 

Тут параметр D и является ключевым.

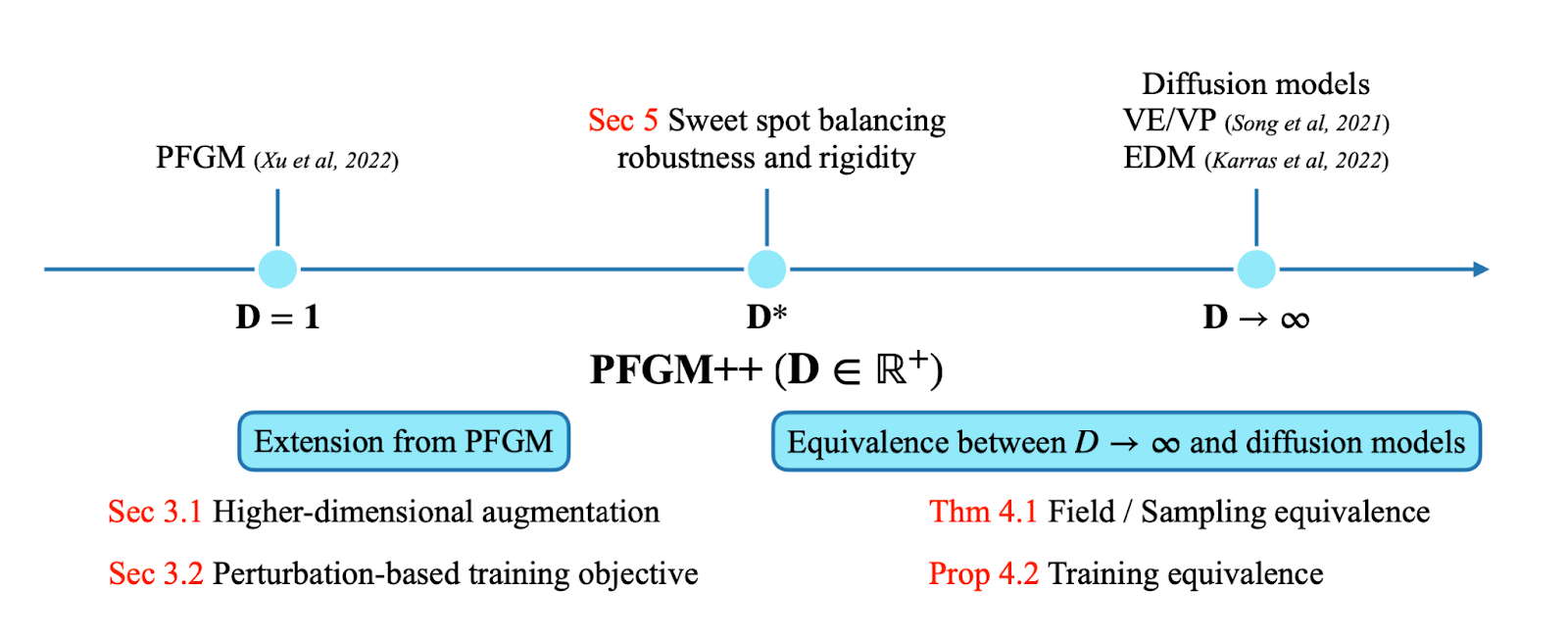
PFGM ++ позволяет исследователям точно настраивать D, который управляет поведением модели. Этот параметр позволяет контролировать баланс между надежностью и ее способностью генерировать высококачественные изображения.

Исследовательская группа провела обширные эксперименты, чтобы продемонстрировать эффективность PFGM ++. Они сравнили модели, обученные с различными значениями  параметра D, включая D →∞ (представляющие диффузионные модели), D = 64, D = 128, D = 2048 и даже D = 3072000.

Модели с определенными значениями D, такими как 128 и 2048, неизменно превосходят современные диффузионные модели на эталонных наборах данных, таких как CIFAR-10 и FFHQ. В частности, модель с параметром D=2048 достигла впечатляющей минимальной оценки FID в 1,91 балла на CIFAR-10, что значительно превосходит предыдущие диффузионные модели.

Таким образом, PFGM++ представляет собой мощное обобщение диффузионных моделей, позволяющее пользователям генерировать изображения более высокого качества за счет повышения устойчивости генерации изображений к возмущениям и ошибкам обучения. 

Будем ждать Вас в комментариях! Спасибо за прочтение :) 

Автор: Черенковская Анастасия