
Задача 1
Стоит девушка с изящными, натренированными, а главное, оголенными ножками. Скучает. Перед тем как демонстрировать свой (n+1)-ый уровень владения техникой пикапа, хочется получше рассмотреть ножки девушки — а стоит ли овчинка выделки? Получше рассмотреть — это под наибольшим углом. Можно незаметно подходить к девушке (типа вдаль смотришь), но приседать нельзя — надо же как-то и приличия соблюдать. С какого расстояния ножки видны под наибольшим углом? Допустим, Ваш рост таков, что глаза находятся на высоте m над поверхностью земли. Ноги девушки оголены до высоты f.
Решение
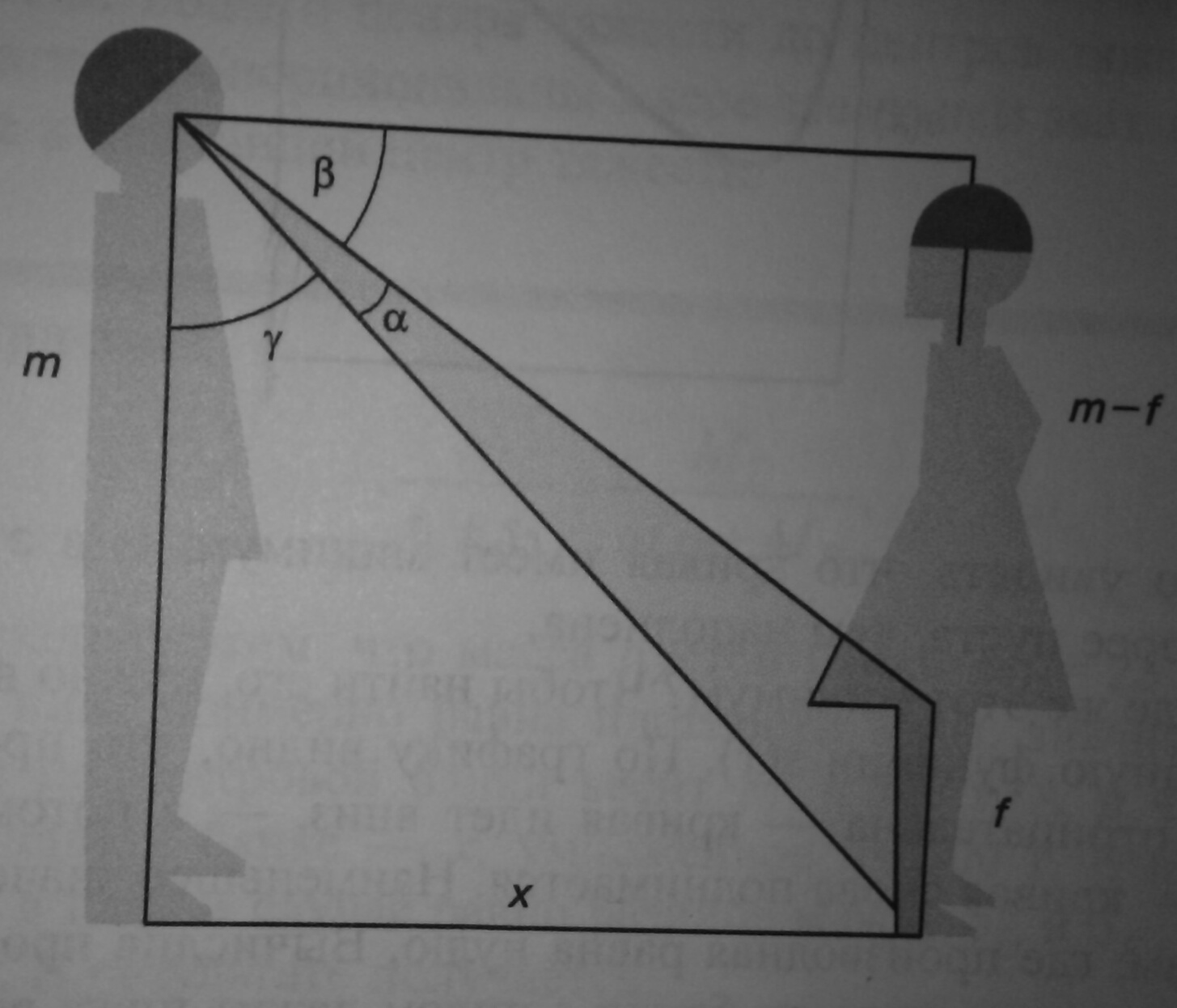
Картинка и перефразированная задача из «Кристоф Дрессер: Обольстить математикой. Числовые игры на все случаи жизни. Бином. Лаборатория знаний, 2015»
Поясним проблему. Издалека плохо рассматривать ноги — они видны под слишком малым углом. Но и если подойти слишком близко, ноги тоже будут видны под малым углом. Где-то должно быть оптимальное расстояние.
Пусть x — расстояние до девушки, f — длина оголенной части ног девушки, alpha — угол, под которым ноги видны (надо максимизировать).
Угол alpha проще всего найти, вычитая из прямого угла углы beta и gamma. Если школьная тригонометрия еще как-то жива в закоулках мозга, легко получим, что
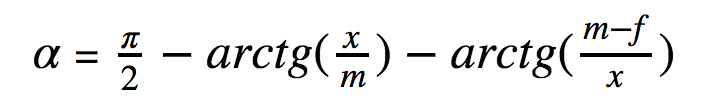
Задача сводится к максимизации alpha(x) по переменной x.
Ну это тоже просто, скажем мы: зануляем производную — и вперед!
Для начала построим график функции alpha(x). Для определенности возьмем значения пераметров m=1.7 м и f=0.7 м (хотелось бы 1 м, но все же предполагается, что имеется некая юбка).
Теперь код. Используется сборка Anaconda и тетрадки IPython. Код воспроизводим, лежит в репозитории GitHub.
# отключим лишние предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
# магическая команда IPython, чтоб картинки прямо в тетрадке рисовались
%pylab inline
import numpy as np
from math import pi, atan
def alpha(x, m, f):
return pi/2 - atan(x/m) - atan((m-f)/x)
# задаем иксы с некоторым мелким шагом
x = np.arange(0, 6, 0.05)
plot(x, [alpha(i, 1.7, 0.7) for i in x])
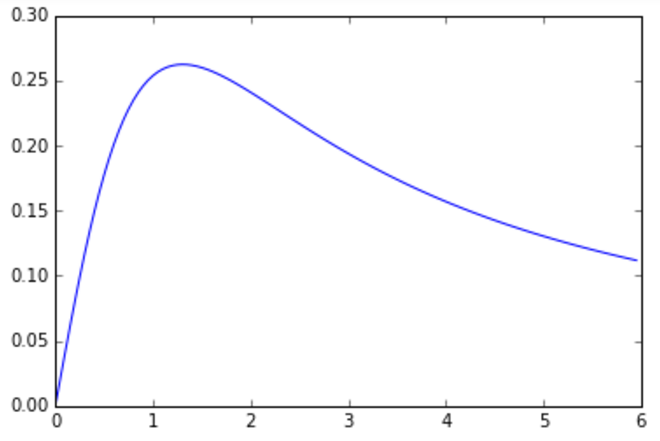
О! Предположение подтвердилось: где-то в 1-1.5 м от девушки ее ноги видны под наибольшим углом. Ну… это уже сложно без палева. Давайте теперь найдем точное значение оптимального расстояния до девушки.
Аналитическое решение «от руки»
Аналитическое решение очень простое, достаточно помнить производную арктангенса. На Хабре LaTeX не поддерживается, так что эта часть в соответствующей тетрадке IPython.
Результат получается такой:
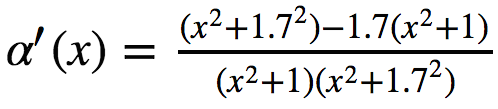
Аналитическое решение с SymPy
SymPy — это библиотека символьных вычислений на языке Python. Мы рассмотрим, как с ее помощью вычислять производные (метод diff) и находить корни уравнений (метод solve).
import sympy as sym
Заведем символьную переменную x и функцию alpha(x). Для символьных вычислений число Пи и арктангенс тоже надо взять из SymPy.
x = sym.Symbol('x')
alpha = sym.pi/2 - sym.atan(x/1.7) - sym.atan(1/x)
alpha # -atan(1/x) - atan(0.588235294117647*x) + pi/2
Посчитаем производную alpha'(x). Методу diff надо указать функцию, переменную, по которой происходит дифференцирование, и порядок производной, в данном случае 1.
alpha_deriv = sym.diff(alpha, x, 1)
alpha_deriv # -0.59/(0.35*x**2 + 1) + 1/(x**2*(1 + x**(-2)))
Можно убедиться, что это то же самое, что получалось, если взять в руки карандаш и бумагу.
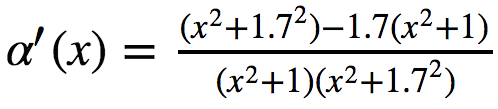
Как видно, к общему знаменателю SymPy просто так выражения не приводит. Для этого есть метод simplify.
sym.simplify(alpha_deriv) # (-0.24*x**2 + 0.41)/((0.35*x**2 + 1)*(x**2 + 1))
Теперь найдем нули производной с помощью метода solve.
sym.solve(alpha_deriv, x) # [-1.30384048104053, 1.30384048104053]
Опять получили, что лучше всего рассматривать девушку примерно с 1.3 м. Интересно, фотографы тоже такие вычисления проводят?
Численное решение c SciPy
Картинка из курса Andrew Ng по машинному обучению
В библиотеке SciPy помимо всего полезного реализованы разные методы численной оптимизации. Подробное описание многих методов минимизации одномерных и многомерных функций даны в документации метода scipy.optimize.minimize.
Метода maximize как такового нет, поэтому задача максимизации будет эмулироваться минимизацией функции, домноженной на (-1). Рассмотрим самый простой случай — минимация скалярной функции одной переменной. Реализованы методы оптимизации 'brent', 'bounded' и 'golden', но отличия почему-то толком не документированы.
from scipy.optimize import minimize_scalar
alpha = lambda x: -(pi/2 - atan(x/1.7) - atan(1/x))
result = minimize_scalar(alpha, bounds=[0., 100.], method = 'bounded')
Ответ прежний, как и ожидалось.
result.x # 1.3038404104038319
Теперь выберем девушку, на чьи ноги будем любоваться. Вернемся к знакомому набору данных girls.csv по моделям месяца по Playboy. Выберем самую высокую из недистрофичных девушек. Заодно покажем кое-что из библиотеки Pandas.
Задача 2
Найти среди моделей Playboy девушку с самым высоким ростом при «нормальном» индексе массы тела — от 18 до 18.5.
Решение
import pandas as pd
girls = pd.read_csv('girls.csv') # объект Pandas.DataFrame
girls.head() # посмотреть 5 первых записей
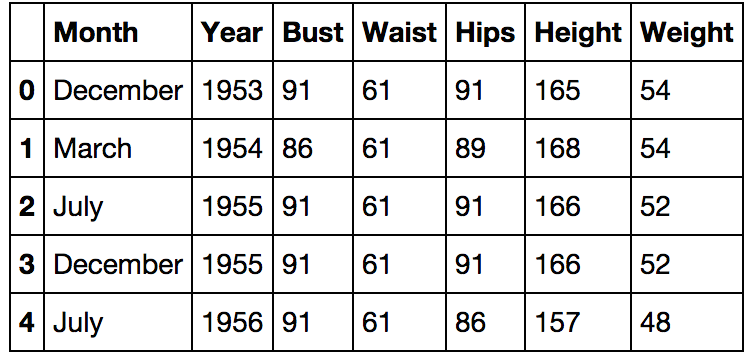
Создадим новый признак BMI — индекс массы тела, равный весу, деленному на рост в метрах в квадрате.
girls['BMI'] = 100 ** 2 * girls['Weight'] / (girls['Height'] ** 2)
Построим гистограмму распределения BMI.
girls['BMI'].hist()

Википедия говорит, что нормальный индекс BMI — 18,5—24,99. Видим, что средний индекс у моделей Playboy примерно на нижней границе нормы.
Отберем девушек с BMI от 18 до 18.5.
selected_girls = girls[(girls['BMI'] >= 18) &
(girls['BMI'] <= 18.5)]
selected_girls.sort(columns=['Height', 'Bust'],
ascending=[False, False]).head(1)
# Month Year Bust Waist Hips Height Weight BMI
#430 July 1994 91 61 91 180 59 18.209877
Это Miss July 1994 по версии Playboy Traci Adell. Дальше поисковик в помощь. Такой выбор вряд ли разочарует.
Итак, мы посмотрели самые основы использования библиотек Python SymPy, SciPy и Pandas. Обилие примеров уже реального использования этих библиотек можно найти в репозиториях GitHub. Один из обзоров таких репозиториев тут.
Комментарии (65)

skjame
27.01.2016 02:04-12такая статья прокатиться только тех вузах для пикапа)

Firsto
27.01.2016 07:21+63Спокойно, парень. Не делай глупостей. Медленно опусти мягкий знак, брось на землю и толкни ногой в мою сторону.

occam
27.01.2016 07:29+5А от кого молодой человек узнает про системный анализ для создания модели вариантов использования? И как обойтись без теории игр, допускающей, что наблюдателей в данный момент может быть несколько и только один игрок с наиболее коротким циклом принятия решения имеет шансы на максимальный выигрыш :-)

yorko
27.01.2016 12:06+3Схожий вопрос, только с позиции девушки, как раз обсуждается в книге «Обольстить математикой. Числовые игры на все случаи жизни», на которую я ссылался в статье. Там вопрос ставится так: «Сколько раз девушке надо отказаться от предложения, чтобы максимизировать вероятность встречи с идеальным женихом»? К вопросу о том, как знакомить с математикой дочь :)

pro100olga
27.01.2016 13:44Класс! А какая полная формулировка задания про жениха?

yorko
27.01.2016 14:53Вкратце и без формул сложно, лучше обратиться к оригиналу. Но смысл такой: у девушки определено отношение предпочтения на множестве потенциальных женихов. «Идеальный» жених существует. Найти зависимость вероятности встречи «принца на белом коне» от количества отказов от предложений руки и сердца.

PatientZero
27.01.2016 09:33+7Трейси Эделл действительно хороша.


yorko
27.01.2016 09:45+3Спасибо! 3-минутный гуглеж мне не помог найти хотя бы одну ее «приличную» фотографию.

random1st
27.01.2016 10:16+1Почему-то навеяло про старый анекдот, как Вовочка умудрился всю физику к хм… единому началу привести.

pro100olga
27.01.2016 10:39+3Интересно, как знакомить с математикой и программированием дочь )

DenimTornado
27.01.2016 11:46+1Вот примерно это пришло в голову…
http://bash.im/quote/395556
Я к тому, что, зачем оно дочери?)
pro100olga
27.01.2016 12:43А зачем оно тогда сыну, если дочери не нужно? )

DenimTornado
27.01.2016 12:44-1Зачем ломать девушке жизнь? А если она ещё и красивая? Красивая и умная, всё, конец…

pro100olga
27.01.2016 12:50А если дочь некрасивая, то математика ей жизнь не поломает, математика так коварна только с красивыми? )
А если сын будет красивым и умным, это не так страшно? )
DenimTornado
27.01.2016 13:00Ну это уже философия) Не та площадка для обсуждения. Вот на каком-нибудь Мегамозге можно.

pro100olga
27.01.2016 13:11Почему же не та. Хабр — площадка для ИТ-специалистов. Среди ИТ-специалистов есть женщины. Чтобы стать ИТ-специалистом, очень вероятно придется учиться математике и программированию. Тем более что дискуссия происходит в комментариях, а не является темой публикации. Или вы просто ненавязчиво сливаетесь? )

DenimTornado
27.01.2016 14:26-2Нет, нет, что вы) Сливаться и не думаю, и это не стереотип (я про коммент ниже), я про жизненный опыт. Умной и красивой девушке тяжелее найти спутника жизни потому как нужно соответствие. Красивых боятся умные парни, умной девочке неинтересно с глупым парнем. Конечно, это ооочень поверхностно, но факт остаётся фактом.

pro100olga
27.01.2016 14:28+1Красивых боятся умные парни
Это внезапно! Почему же они боятся? )
DenimTornado
27.01.2016 14:31-1Ну на этом построен ситком «Теория большого взрыва». Вместо тысячи слов)

pro100olga
27.01.2016 15:08Но в ТБВ из четырех героев в итоге у двоих девушки — доктора наук, еще у одного — врач. Из них разве что Эми можно назвать некрасивой. Да и Пенни далеко не дура. Не думаю, что им надо было выбрать «не ломать себе жизнь» и не учиться.

DenimTornado
27.01.2016 15:23Хм, так там как раз основная суть комедии в том, что у гения получилось с красоткой без образования. И вот тут я, пожалуй, сольюсь, ибо я до вас свои мысли донести, похоже, не в состоянии.

pro100olga
27.01.2016 15:45Мне кажется, ваши мысли просто достаточно противоречивы.
Например, вы говорите что умные мужчины боятся красивых женщин — допустим. Получается, если у человека красивая дочь, то не нужно ее учить (математике или чему-то еще), чтобы она что? Выбрала себе в спутники глупого мужчину, потому что умный будет ее бояться? А то если станет умной и красивой, то даже с глупым не получится, а так типа хоть кто-то ))
В доказательство своего утверждения о том, что умные мужчины боятся красивых женщин, приводите сериал, где половина главных героев (Воловиц и Кутрапали) выбрали себе умных и красивых женщин.
При этом ссылаетесь на свой опыт — неужели среди ваших знакомых умных мужчин все выбирают себе некрасивых женщин, потому что боятся красивых? О.о
Мне кажется, красивых женщин боятся разве что неуверенные в себе мужчины, а не умные. И ТБВ как раз этот случай, там в герое сочетаются эти качества.
Mendel
27.01.2016 16:01Мне кажется что позиция вашего оппонента в том, что у умной женщины хуже выбор женихов.
Исходит он из предпосылки что мужчина обязательно должен быть не глупее женщины.
Не соглашусь с таким подходом потому что помимо того что закрываются варианты «глупый» открываются варианты «умный который не хочет глупую».
Я бы сказал что умными должны быть все, но если барышня академически умна, то ей в большей степени чем менее умной нужна жизненная мудрость. Но в принципе она всем нужна, так что я не сторонник этого «женщине не надо». А тот комментарий вышел был скорее просто «личным» уколом в контексте старого спора.

0xd34df00d
27.01.2016 23:11+2Они не боятся, они вместо того, чтобы подходить и знакомиться, рефлексируют о том, что у такой красивой девушки уже наверняка кто-то есть, а зачем ей я, а вот, а ну…

pro100olga
27.01.2016 13:39+1Или вот например, если красивая дочь внезапно выучит биологию и станет красивой и умной ученым-биологом, это тоже конец, или только математика так опасна? ) Сорри за легкий троллинг, но меня искренне удивляют стереотипы «ты же девочка, зачем тебе математика». Всегда интересно разобраться, почему люди так думают.

Mendel
27.01.2016 15:35-1Потому что «ученый-биолог» будет сдавать кандидатский минимум.
Потому что без фальсифицируемости и проверяемости ее выслушают, и пошлют обосновывать, проверять и т.п.
А в «бытовой математике» можно и бездоказательную охоту на ведьм устроить, да еще и утверждать что это типа научная позиция. Конечно мужчина с поверхностными знаниями отмочит не меньшую глупость. Но у мужика не пройдет «ой всё!», и мужику меньше будут прощать рецензенты ориентируясь на гендерные моменты.

Puzzle
27.01.2016 16:24Мужчины по своей природе более склонны «копаться под капотом у автомобиля», чем девушки. Безусловно, такие склонности встречаются и у девушек. В этом им помогает повышенный андрогенный фон.

pehat
30.01.2016 01:19-1Прочитал Ваш комментарий 3 раза, пока между словами «чем» и «девушки» не исчез предлог «у». Видимо, я слишком испорченный.

yorko
27.01.2016 12:02хм… фигурное катание? балет? виолончель?

pro100olga
27.01.2016 12:43Знакомить с математикой с помощью фигурного катания и виолончели?

atikhonov
27.01.2016 13:33+2сначала виолончель, а потом раз так, смотри дочь, и geom_violin()

pro100olga
27.01.2016 13:36:)) вообще, я выбором виолончели удивлена, тяжелый ведь инструмент. Пианино — вот типично gender-specific инструмент.

Mendel
27.01.2016 15:41+1Для вас фортепиано легче потому что вам не приходилось заносить его на девятый этаж.

Stas911
27.01.2016 16:59+1Видел как-то пост, как девушка-статистик мощно захачила сайт знакомств и в итоге успешно нашла себе вторую половинку.

pro100olga
27.01.2016 23:33Отлично ) А почему она так не могла его найти на этом сайте, зачем надо было взламывать сайт? )

un1t
27.01.2016 11:12+1Код воспроизводим, лежит в репозитории GitHub.
А где собственно код? На гитхабе только картинки и csv.

andreymironov
27.01.2016 12:26-5Никаких приличий! Не позднее, чем через 3 секунды после первой невербалики подходишь, открываешь ситуативным опенером, спрашиваешь об имени с лёгким кином по рукам, заинтересовываешь, даёшь пару нег-хитов, голос доры, берёшь телефон и закрываешь коммуникацию на интересном подъёме. Этап 0 завершён. Смыть, повторить 100 раз.

barkalov
27.01.2016 20:52+3А тазом двигать надо?

0xd34df00d
27.01.2016 23:16В голове от прочтения возникла забавная картина, больше всего понравился голос доры, да.

rg_software
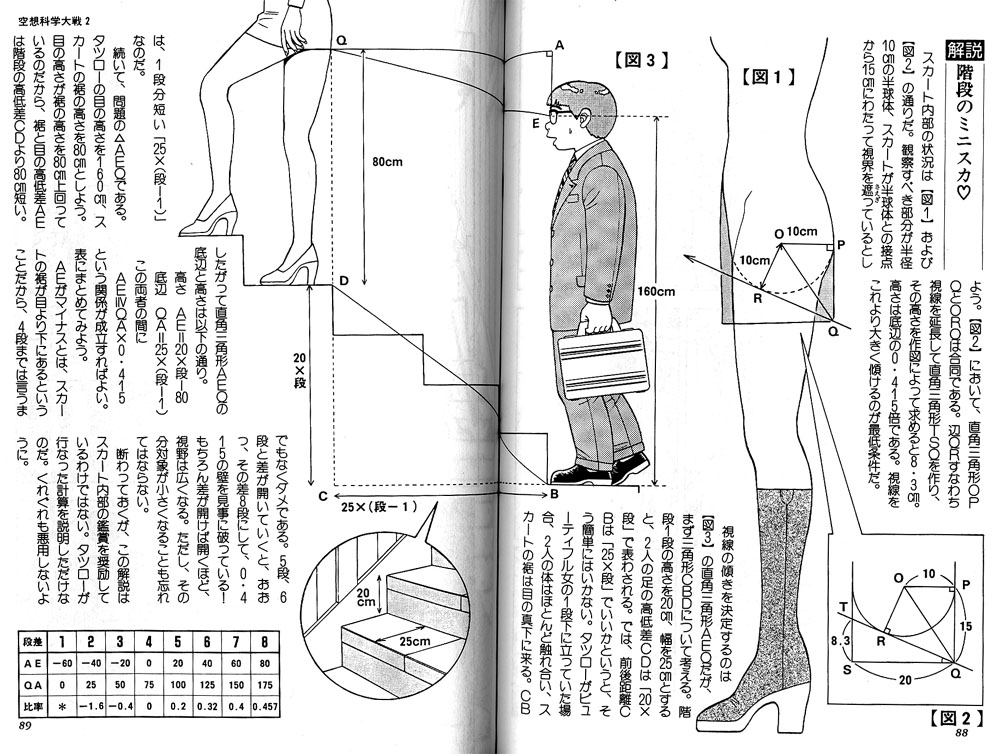
28.01.2016 11:19+3Японцы уже осваивали идею:

m03r
31.01.2016 13:58а как это переводится?

rg_software
31.01.2016 16:12Я этот текст полностью не осилю :) Но это из какого-то стёбного учебника, очевидно, обычный нормальный учебник в Японии столь же обычен, как и у нас.



WinPooh73
Вот, наконец, и конструктивное доказательство известной теоремы, сформулированной ещё Ландау. О том, что есть расстояние, с которого женщина выглядит наиболее привлекательно (т.к. для расстояний 0 и бесконечность оптимум, очевидно, не достигается).
1vanK
А как насчет отрицательных расстояний? )
iCpu
Всмысле, изнутри? Не думаю, что вам понравятся бабочки в животе и их куколки за грудиной, а ведь там в голове ещё и тараканы водятся.
yorko
А можно поделиться этими мыслями корифея? Вспоминается только формула привлекательности женщины.
Kolegg
Про себя он говорил, что у него не телосложение, а теловычитание.
BalinTomsk
Думаю пора внести в формулу количество выпитого, массы выпиваюшего и степень увеличения привлекательности при этом.