Часть 2 >>

Введение (Языковая природа абстрактных понятий)

Цель этой работы показать, как языки наподобие английского, в качестве естественного и эффективного метода могут возникнуть на различных уровнях процесса восприятия. Попутно затронуты вопросы механизмов, позволяющих нам и животным видеть, классифицировать по форме цветовые пятна, составлять представление о местах, предметах и их геометрических свойствах. Несколько слов посвящено чисто языковым проблемам: тому, какие понятия и методы должны присутствовать в любом достаточно выразительном описательном языке среди первоначальных, а какие, в качестве производных, из первоначальных могут быть получены.
Каким же образом мог бы участвовать язык, например, в процессе зрительного восприятия? Каждый из нас привык говорить о своей способности видеть дерево, слышать пение птиц и чувствовать тепло, держа руку над свечой. Тем не менее нашему сознанию ни звук, ни тепло, ни ощущение света не доступны для восприятия непосредственно. Представление обо всем этом формируется исключительно на основании свойств и закономерностей раздражения наших рецептов. Чтобы понять сложность задач, возникающих в таких случаях перед мозгом, представьте себе, что, вместо привычного способа созерцания самой обычной кошки, у вас «букет» из полусотни лампочек на проводах, отвечающих раздраженности светочувствительных рецепторов сетчатки глаза. Попробуйте теперь исключительно в терминах того, какие из ламп горят а какие нет, сформулировать, что такое кошка. Не правда ли, при решении этой задачи возникает желание записать, в какой последовательности упомянутые лампы загораются или гаснут. Сам процесс создания такой записи уже является зачатком (прим. для переводчика: имелось в виду seed) языковых методов.
Предположим, некоторое время понаблюдав за лампами и поразмыслив, вы дали какое-нибудь исчерпывающее определение понятию «кошка».Тогда естественным был бы вопрос его универсальности: если кто-то другой, имея тот же букет ламп, исчерпывающе определит, что такое «кошка», совпадут ли ваши определения? Чтобы прояснить ситуацию, возьмем пример попроще. Представьте себе букет из семи ламп, отражающих состояние семи светочувствительных рецепторов, расположенных как на рис.1a

Если лампы совершенно одинаковы и нет никакого способа решить по любой из них, каково место связанного с ней рецептора, то во избежание путаницы было бы разумно каждую из этих ламп пометить номером. В соответствии с нумерацией рисунка 1а фигура, именуемая здесь «черная косточка» (рис 1б) может быть исчерпывающе описана простым перечислением того, под какими номерами лампы горят, а под какими нет.

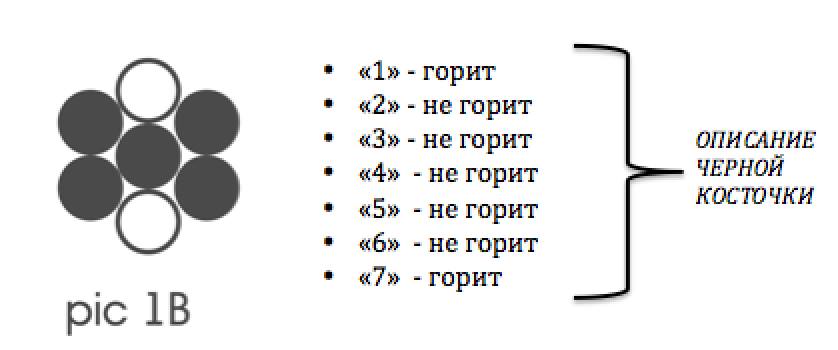
К сожалению, подобные определения косточек ни на какую универсальность не претендуют, поскольку нет каких-либо предпосылок, чтобы разные люди нумеровали лампы одинаково. Это немного напоминает тот факт, что даже у похожих внешне народностей одни и те же понятия, к примеру солнце, имеют разные названия.
Известно, что глаз насекомого состоит из множества самостоятельных маленьких глазков, расположенных подобно ячейкам в пчелиных сотах. Очевидным способом конструирования природой зрения насекомого (это лишь разумная догадка) было бы связать с каждым таким глазком свой маленьких промежуточный отдел мозга, в задачи которого входило бы составлять описание текущего изображения на сетчатке глазка и передавать это описание к вышестоящим отделам. Чтобы насекомому понимать, что разные глазки наблюдают на самом деле один и тот же предмет и отслеживать положение этого предмета, крайне предпочтительно было бы иметь метод, позволяющий промежуточным отделам для одинаковых изображений строить одинаковые описания, независимо от того, на сетчатке какого глазка такие изображения появляются (рис.2).

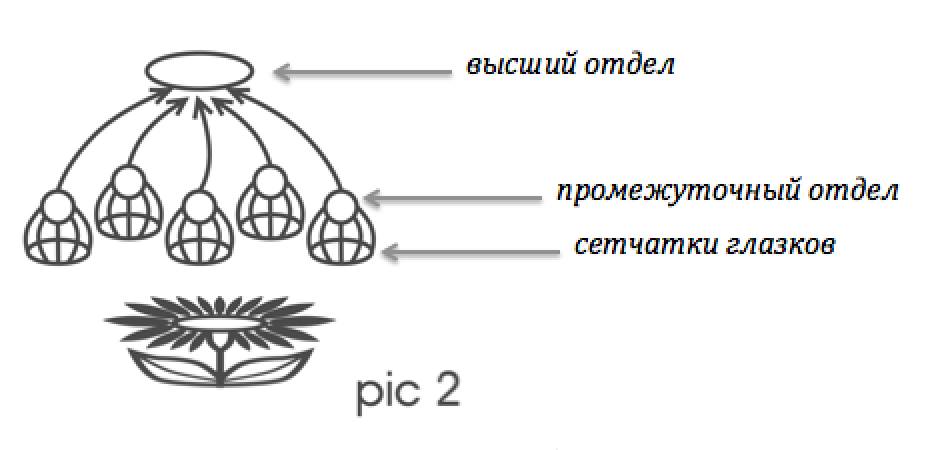
Подобным методом могло бы стать описание изображений исключительно в геометрических терминах, лишенное соотнесения с какой-либо нумерацией. Однако не стоит забывать, что определение всех этих «геометрических терминов» должно быть предварительно дано все через те же аморфные букеты ламп.
Вопрос, родственный только что описанной проблеме, — каким образом у человека процесс узнавания формы цветовых пятен устроен так, что он не зависит от положения этих пятен в поле зрения, и как дать такую же возможность машинам. Пусть некоторая машина или живой организм уже способны классифицировать форму цветовых пятен и их взаимное расположение. Достаточно ли этого для возможности образовывать понятия о местах и предметах? Ключевой особенностью мест и предметов является то, что их невозможно, в отличие от цветовых пятен, наблюдать целиком: как бы вы ни вращали собранный кубик Рубика, увидеть одновременно больше трех его граней у вас не получится. Каждый имеет представление о своем городе или селе, но в них наверняка много таких мест, которые нельзя увидеть разом.

В первой части ближайшего повествования на крайне простом примере будет показано, как в терминах рецепторов цвета и движения определить основные геометрические понятия. Вторая часть посвящена симметриям и тому, как инвариантным образом по отношению к положению в поле зрения может быть определена форма, а в третьей — исследуются средства, необходимые для формирования понятий «предмет» и «место».

Геометрические понятия гексагональной решетки

Чтобы проиллюстрировать, как в процессе восприятия возникает представление о свойствах геометрического характера, возьмем достаточно простой пример из воспринимаемого объекта такие свойства в себе заключающего и воспринимающего – способного их заметить. Этими объектами будут нам служить гексагональная решетка, раскрашенная самым произвольным образом в черный и белый цвет подобно политической карте, и зонд из семи цветочувствительных рецепторов, соединенных рамкой, способной над этой решеткой перемещаться.

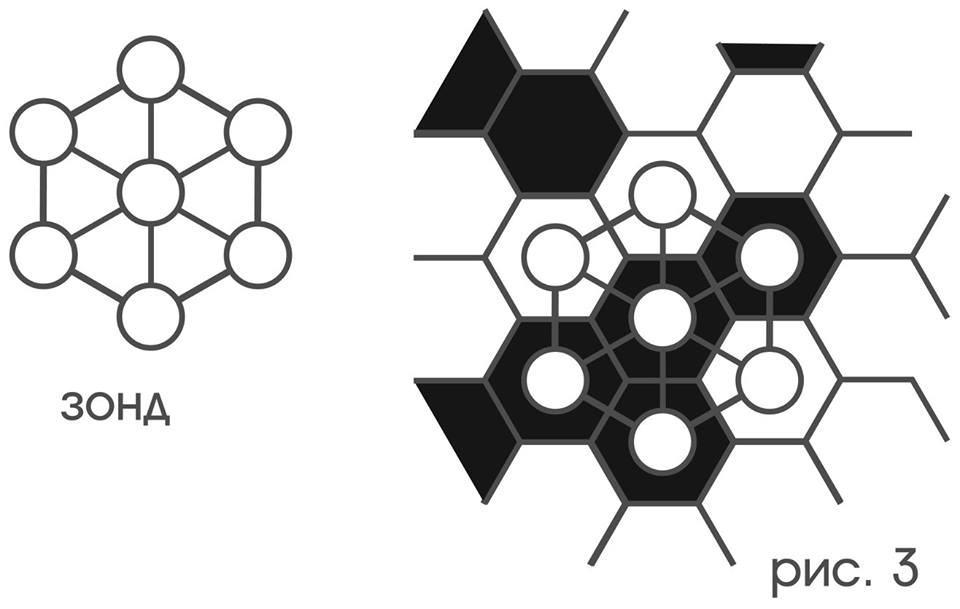
Для удобства описания перемещения зонда жестко свяжем его с циферблатом так, чтобы рецепторы оказались напротив отметок «2», «4», … «12» (рис 4).

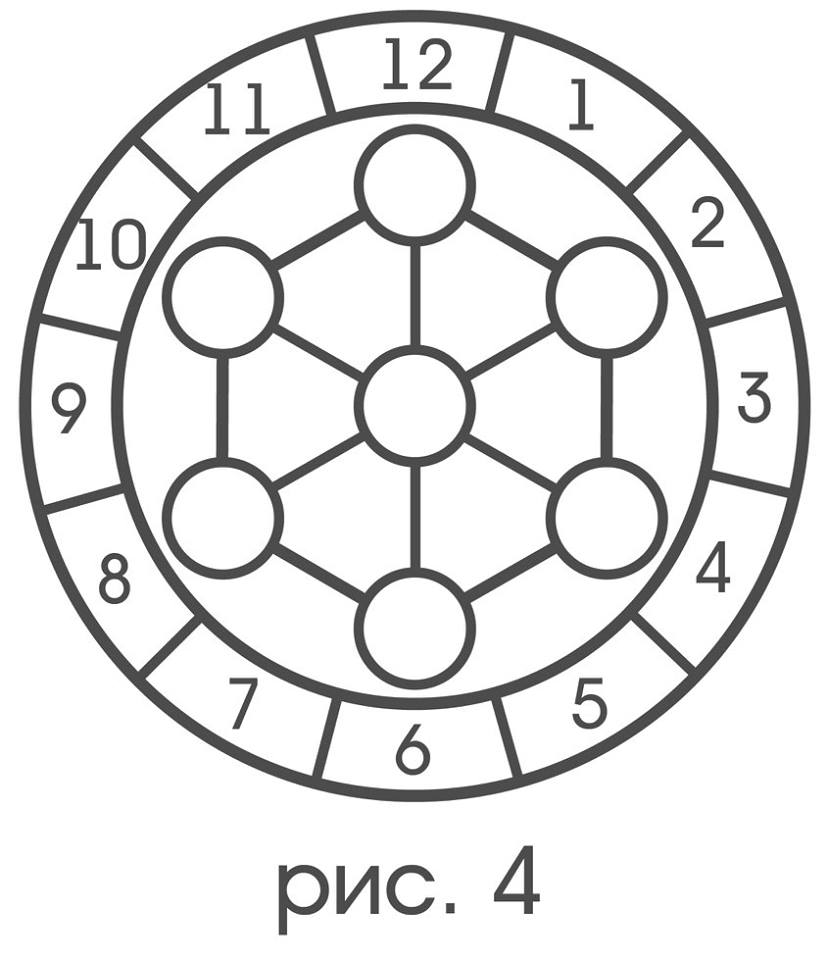
Если это сделано, то каждая инструкция вида: «сместить зонд параллельно себе в направление «2» на 6 клеток, затем повернуть его она треть оборота против хода часовой стрелки, после чего вновь сместить в направлении «12» на 4 клетки» определяют некоторый тип движений (считается, что циферблат поворачивается вместе с зондом). Среди этих типов особо выделим плоскопараллельные смещения на одну клетку в направлении «2», «4» … «12», для краткости обозначая их соответственно как ,?,…^, а также повороты вокруг центрального рецептора на 60° по ходу часовой стрелки — ? и против — ?. Первые будем называть элементарными смещениями, а вторые – элементарными поворотами. Предполагается, что зонд способен мгновенно скачком выполнять движения некоторых типов, среди которых обязательно присутствуют элементарные смещения, но не обязательно элементарные повороты.
Движения таких типов назовем простыми для зонда.
Следуя общей идеи повествования, будем считать, что к цветочувствительным рецепторам подключен произвольным образом, возможно никак не отражающим их взаимного расположения, букет из семи одинаковых на вид ламп, каждая из которых горит в точности тогда, когда связанный над ней рецептор находится над белой клеткой (рис 5а).

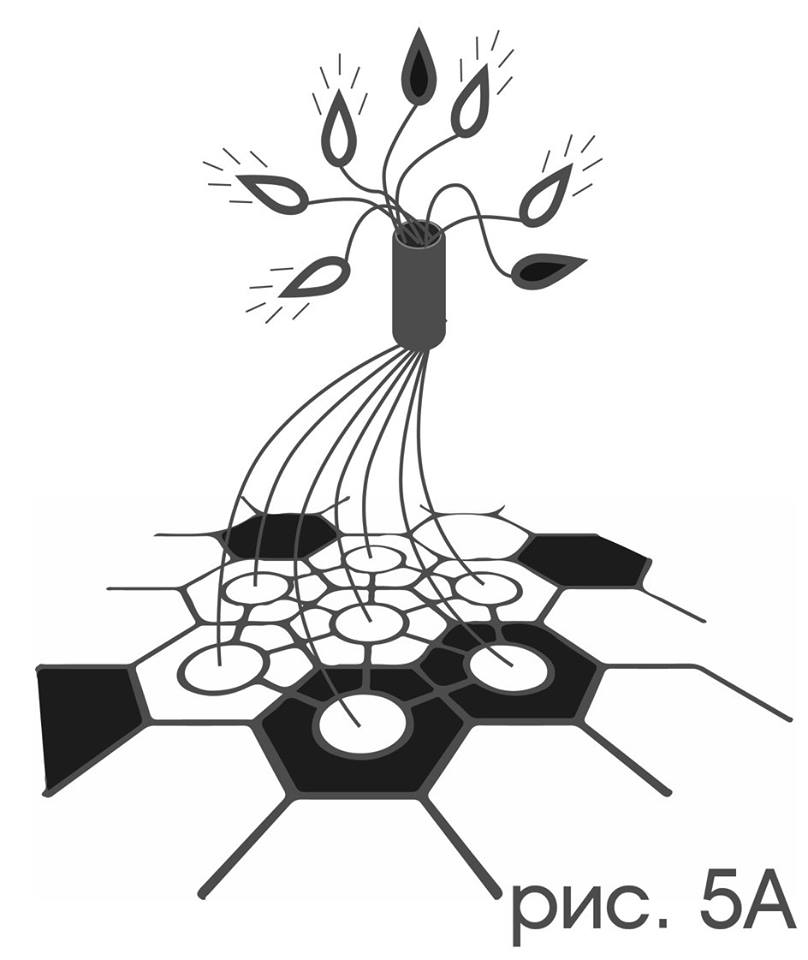
Простые движения будем отслеживать с помощью другого букета ламп: каждая его лампа гаснет в те моменты, в которые происходят движения типа, представляемого этой лампой.

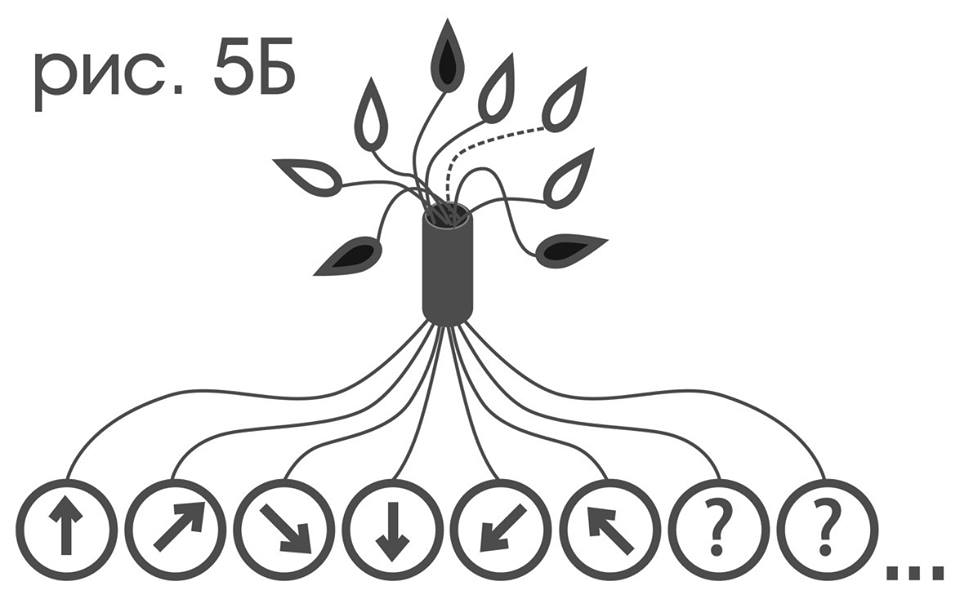
Здесь также предполагается отсутствие какой-либо возможности лишь по виду ламп определить типы, представляемых ими движений. Но нельзя ли это сделать другим способом?
Сократ в одном из «Диалогов Платона» заметил, что если в селении живет только один художник, то свойство быть художником однозначно называет этого человека или, то же самое, является для него категоричным. Связь зонда с индикаторами порождает следующую двойственность: всякому явлению, наблюдаемому по отношению к цветочувствительным рецепторам и движениям зонда, дуально явление, наблюдаемое по отношению к его индикаторам; всякой же закономерности, которая может быть сформулирована лишь в терминах движений и воспринимаемых рецепторами цветов, дуально соответствует закономерность, выразимая исключительно в терминах его индикаторов. Естественной, поэтому, является попытка настолько категорично охарактеризовать, какие именно явления или какие именно закономерности соответствуют друг другу, чтобы, наблюдая только за индикаторами, смочь сказать, что же происходит в этот момент с зондом.
Переход от определения некоторого понятия к определению двойственного ему понятия назовем переводом. Договоримся всюду, где это возможно, давать одинаковые имена двойственным понятиям, при этом говоря о собственном смысле этих имен, когда они называют понятия, относящиеся непосредственно к зонду, и несобственном смысле, когда речь идет о явлениях, связанных с его индикаторами. В качестве иллюстрации попытаемся в двойственных терминах охарактеризовать класс элементарных смещений и свойства рецепторов «быть центральным».
Может наблюдаться такое явление, что всякий раз сразу после завершения движения типа p цветочувствительный рецептор x всегда оказывается над той же самой клеткой, над которой непосредственно перед выполнением этого движения находился рецептор y.
Пусть рецепторы помечены буквами A,B,…G как на рис.6,

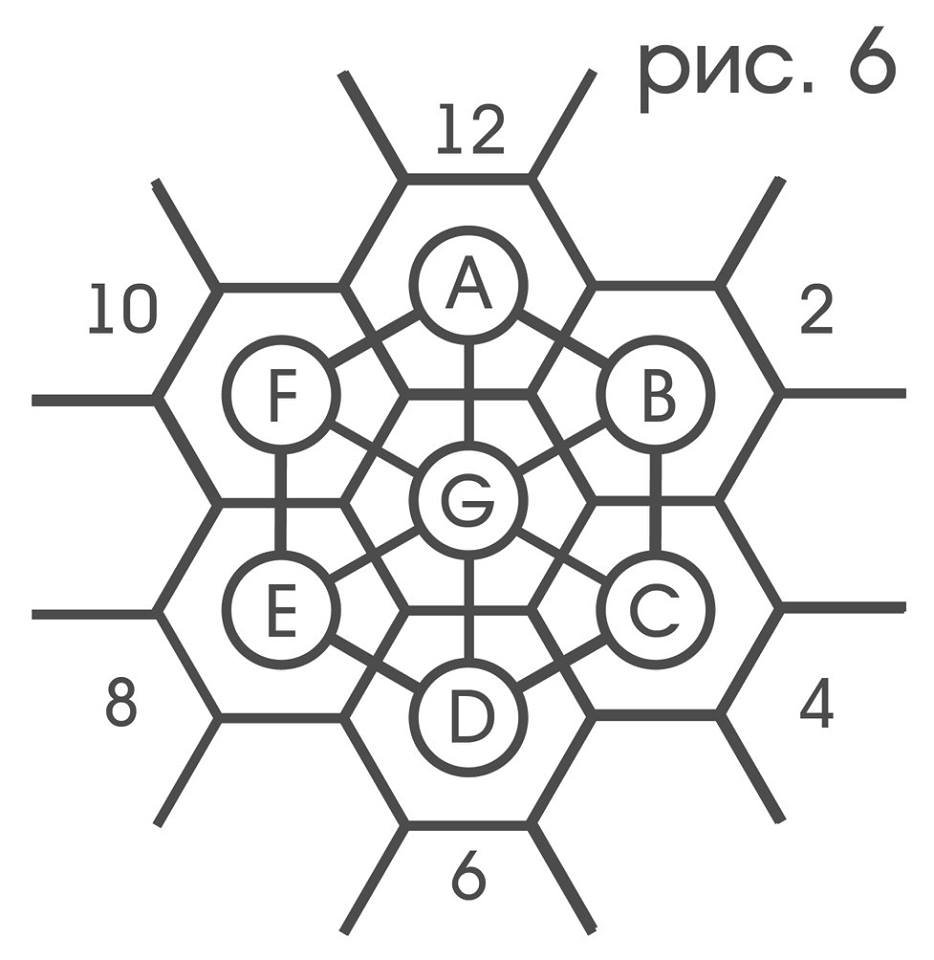
тогда G после смещения ^, всегда оказывается на том месте, где этого находилась A;

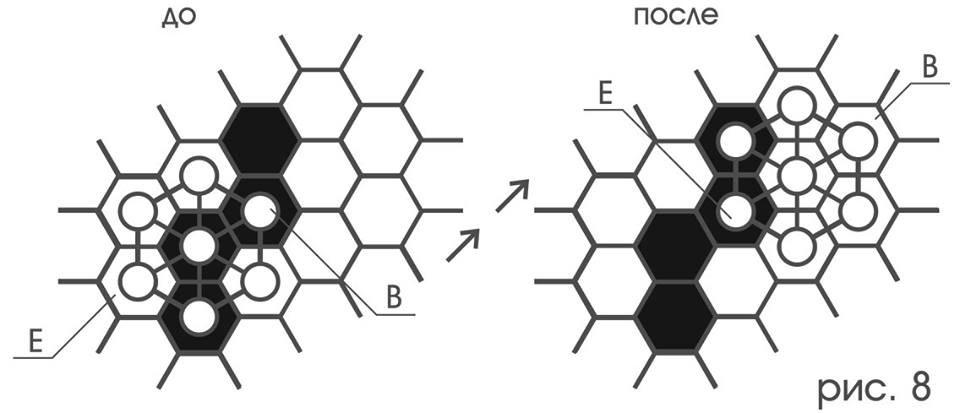
E после двойного смещения на ? всегда оказывается на том месте, где до этого находилась B;

всякий раз после поворота вокруг C на 60° по ходу часовой стрелки C остается на своем месте, а E оказывается там, где до этого находилось A.

Внимательное рассмотрение приведенных иллюстраций наталкиевает на мысль, что то же самое явление можно определить без упоминания о клетках решетки — исключительно в терминах рецепторов, типов движений и цветов:
“будем говорить, что рецептор y лежит по направлению движения P от рецептора x, если всякий раз после завершения движения типа P цветочувствительный рецептор x воспринимает тот же самый цвет, который непосредственно перед выполнением этого движения воспринимал y”.
С другой стороны, как это уже отмечалось, для всякого понятия, определимого лишь в терминах рецепторов и типов движений, существует двойственное к нему понятие, определимое в терминах индикаторов. Что касается понятия «лежать по направлению», то двойственное к нему имеет следующую очевидную формулировку:
«будем говорить, что индикатор цвета y лежит по направлению движения, определяемого индикатором P, от индикатора x, если всякий раз сразу после того момента, когда гаснет индикатор P, индикатор x оказывается в том же состоянии, в котором находился y непосредственно перед указанным моментом»
В соотвествии с этими двумя определениями фраза “x лежит по направлению P от y”, когда вместо x и y подставляются какие-нибудь имена рецепторов зонда, а вместо P – имя типа его простых движений, приобретает собственный смысл, описывая отношениями между парами рецепторов и типами движений. Когда же вместо x и y подставляются какие-нибудь имена индикаторов цвета, а вместо P – имя индикатора движений, эта фраза имеет несобственный смысл и описывает отношения между парами индикаторов цвета и индикаторами движений. Для сокращения в обоих случаях вместо «x лежит по направлению P от y» договоримся писать x (P) y.
Мы часто говорим о вещах, не называя их конкретно: “неизвестный, ограбивший вчера банк”, “лошадь, которая придет на завтрашних скачках первой”. Именно в этом, чисто назывательном смысле, будет пока употреблять фразы “индикатор, связанный с рецептором x” (сокращенно n[x]) и «индикатор, представляющий простые движения типа P» (сокращенно n[P]), не предполагая существования никакого конкретного способа узнать, какая именно лампа связна с x или представляет P. В введенных таким образом обозначениях можно утверждать, что
G(^)A и n[G](n[^])n[A] (рис.7)
E(?*?)B и n[E](n[?•?])n[B] (рис.8)
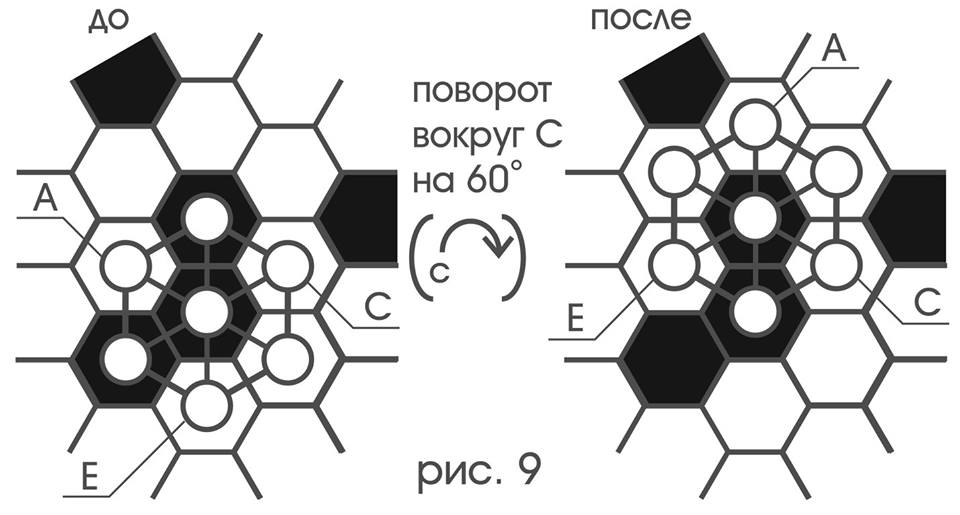
C(?_C )C и n[C](n[?_C])n[C] (рис.9)
E(?_C )A и n[E](n[?_C])n[A] (рис.9)

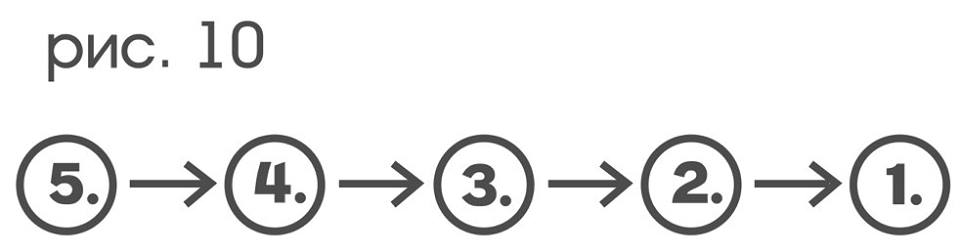
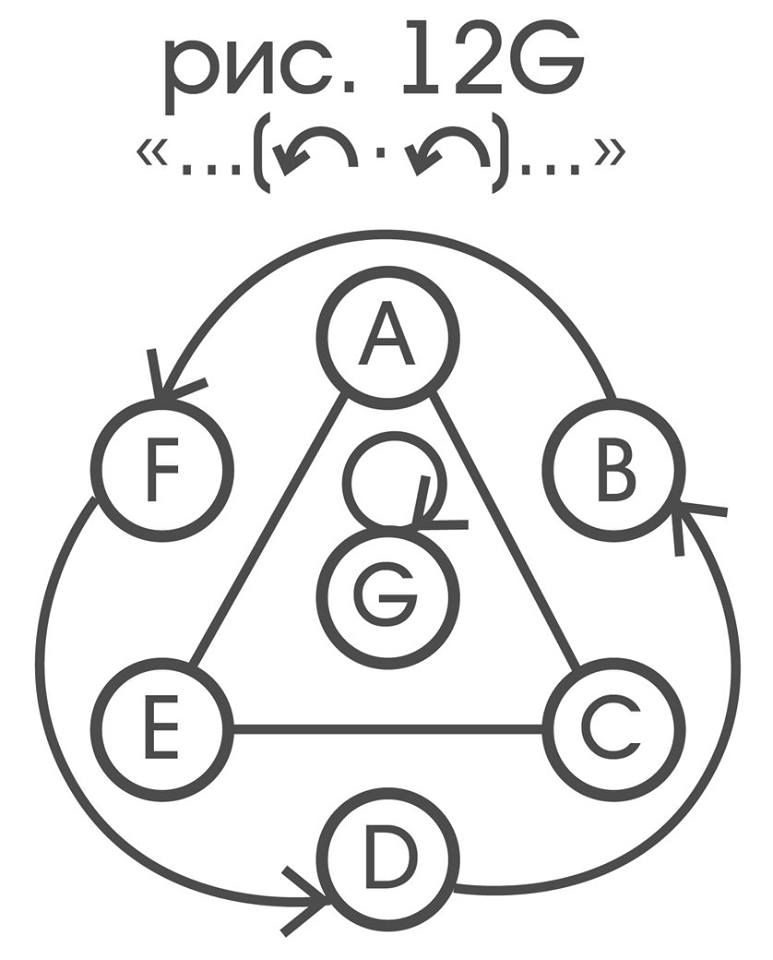
Фиксация любого простого типа движений p дает двуместное отношение …(p)… на множестве цветочувствительных рецепторов зонда, при этом фиксацией индикатора движения q получается двуместное отношение …(q)… на множестве индикаторов цвета. Двуместные отношения на множествах удобно изображать ориентированными графами: для этого нужно соединить стрелками те элементы множества, которые находятся в данном отношении. Иллюстрируя сказанное, возьмем множество чисел {1,2,3,4,5} и отношение «следующий по счету за», тогда оно изобразится графом:

Если на том же множестве взят отношение “быть меньше, чем”, то его графом будет:

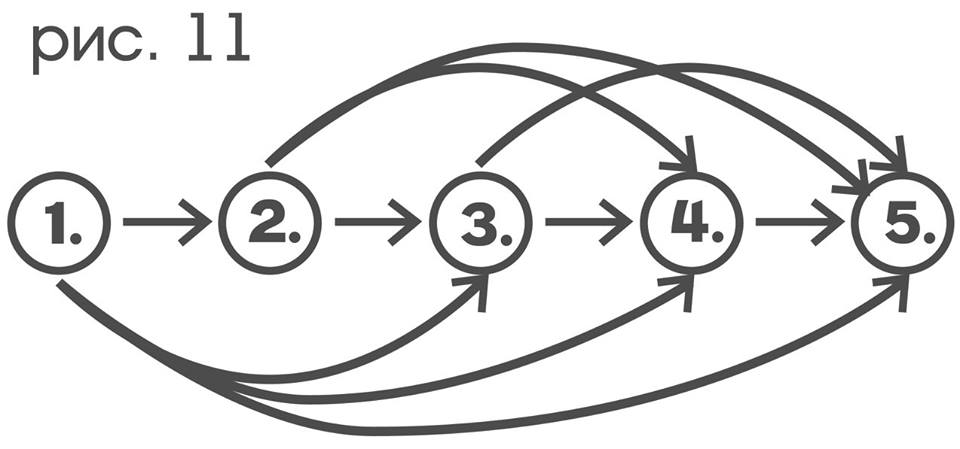
где, например, стрелка от 2-ум к 4-ем означает, что 2 меньше 4-ех.
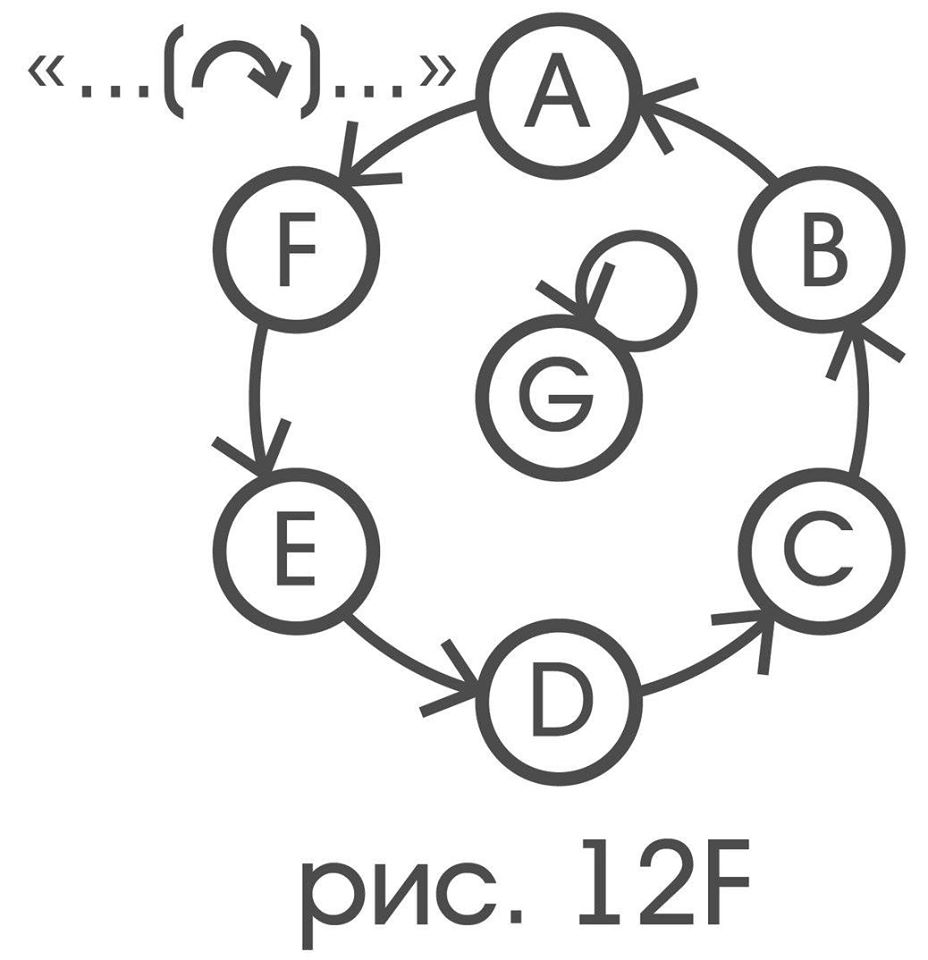
Графом отношениям «…(^)…» (означает :“…” в направлении ^ от “…”) будет

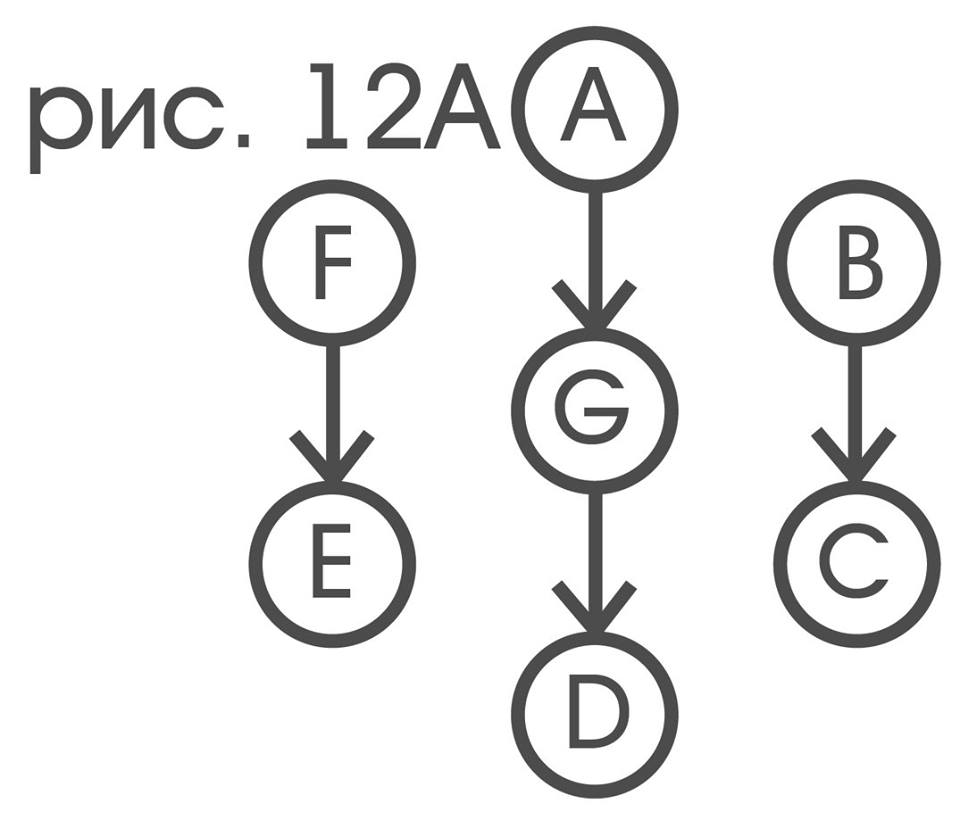
граф же ему двойственного отношения «…(n[^])…» получается простой заменой имен рецепторов на имена индикаторов, с ними связанных.

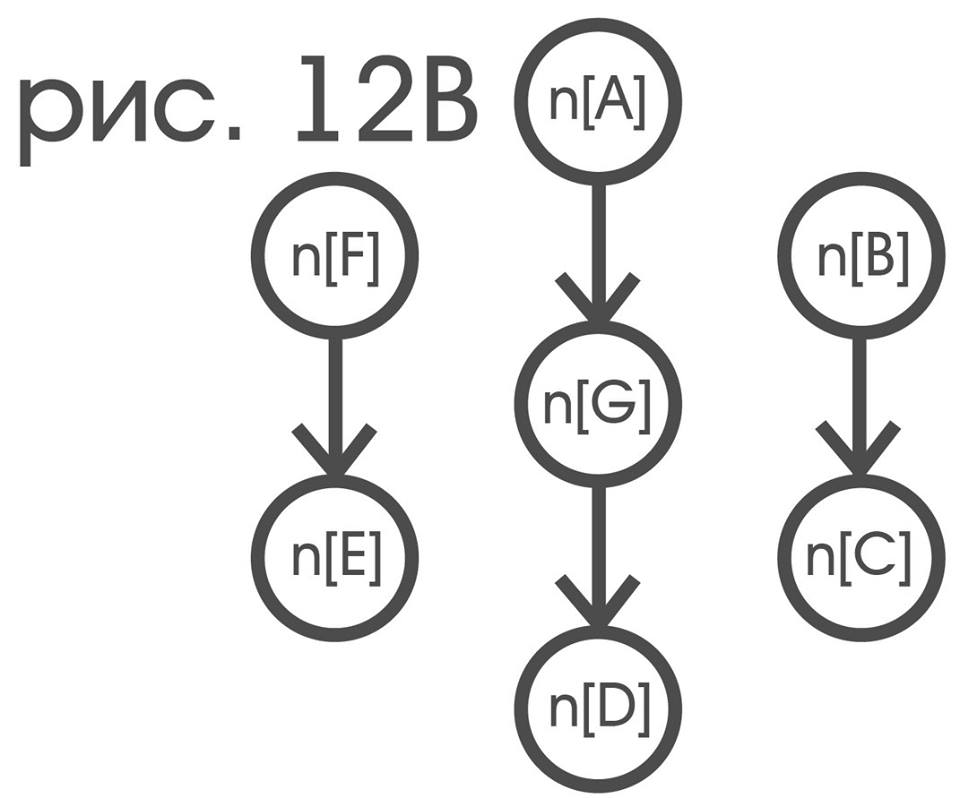
Ниже приведены графы еще нескольких отношений:
«…(v)…»

«…(?)…»

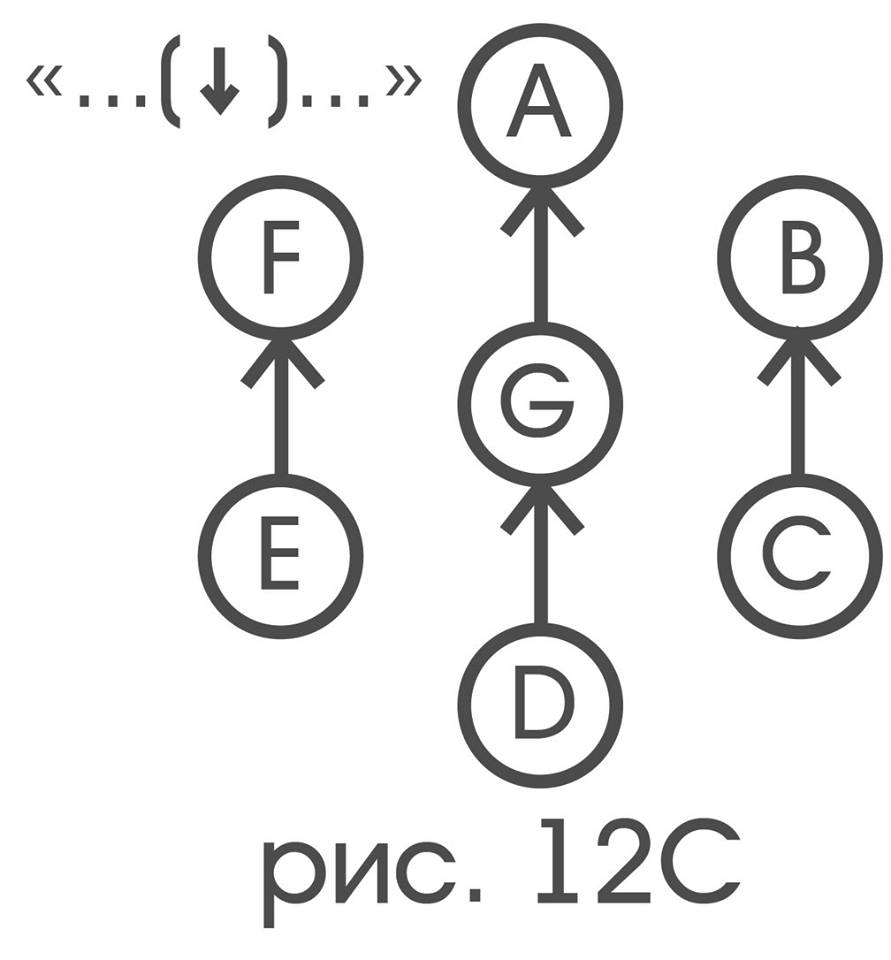
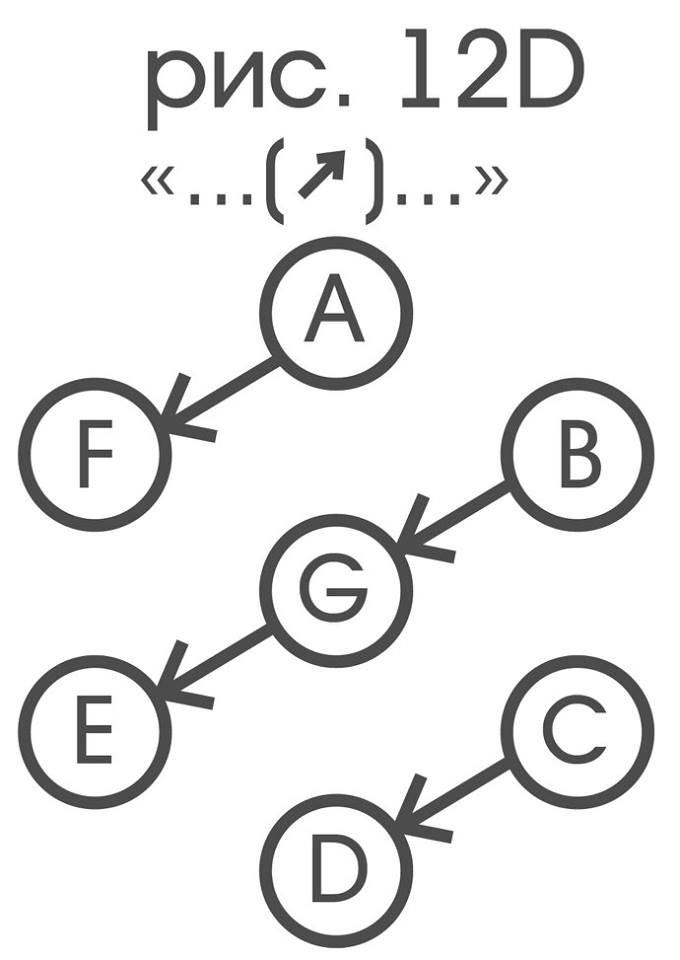
“…”лежит в направлении двойного смещения ? от “…”

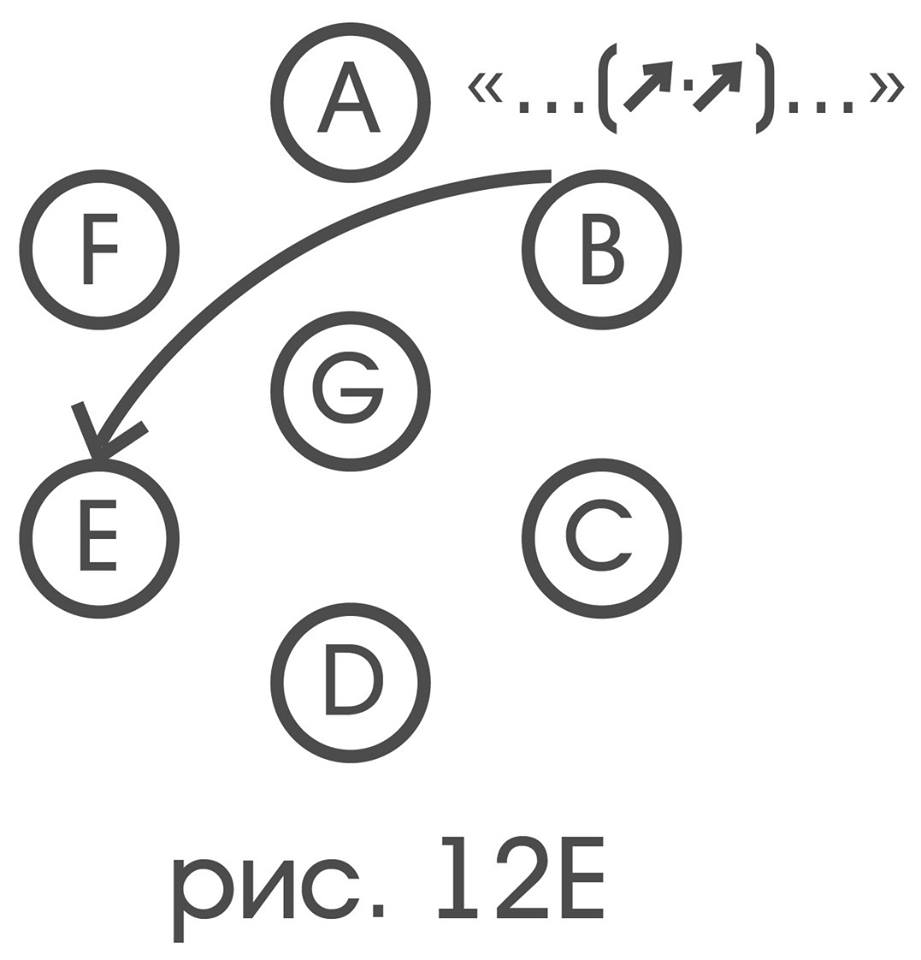
«…(?)…» (“…”лежит в направлении поворота вокруг G на 60° — по ходу часовой стрелки от “…”)

«…(?*?)…» (“…”лежит в направлении поворота вокруг G на 120° — против хода часовой стрелки от “…”)

«…(?_C)…»

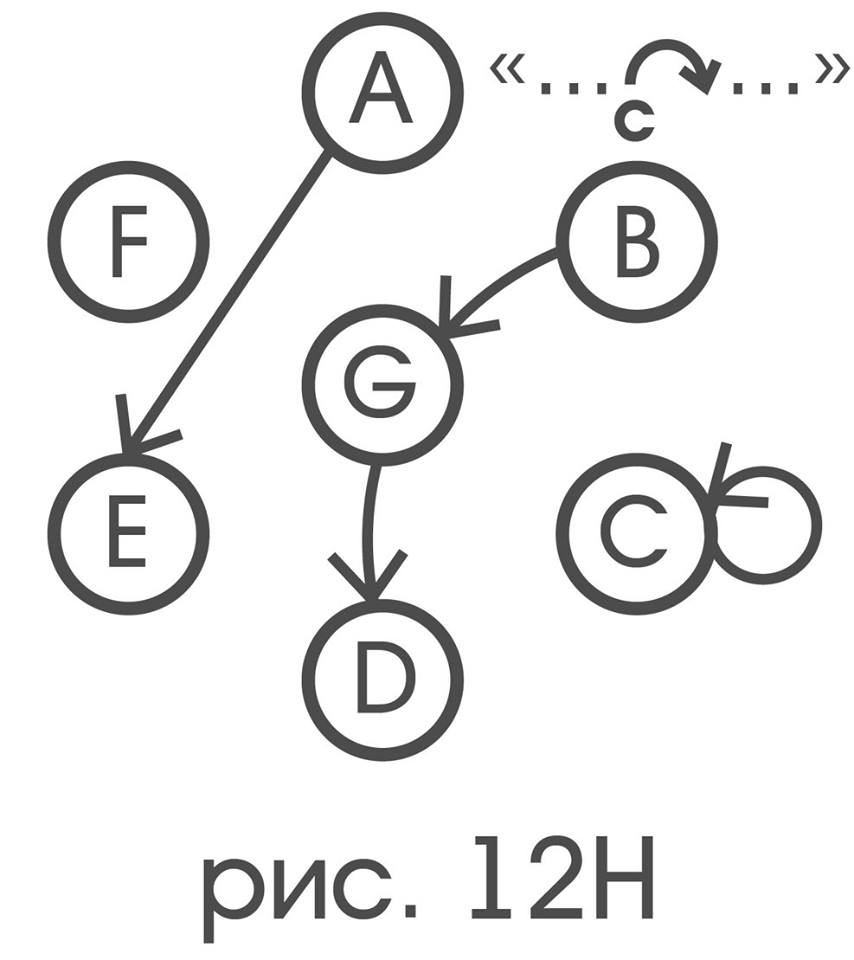
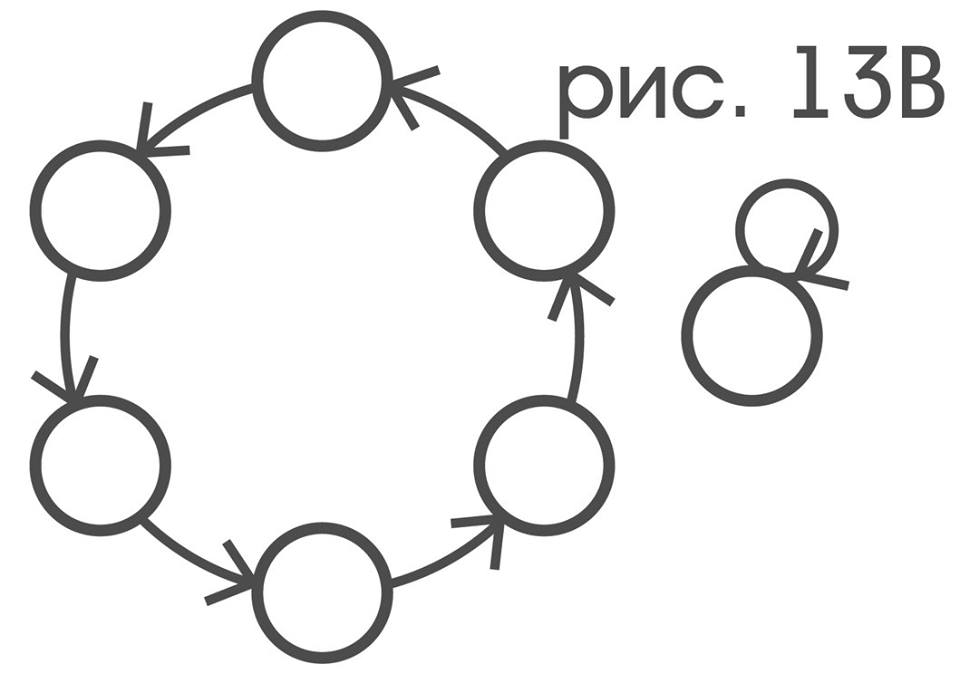
Если теперь в нарисованных графах стереть буквы, получится то, что естественно называть их структурами. Обычным перебором можно показать, что только элементарным смещениям соответствует структура S:

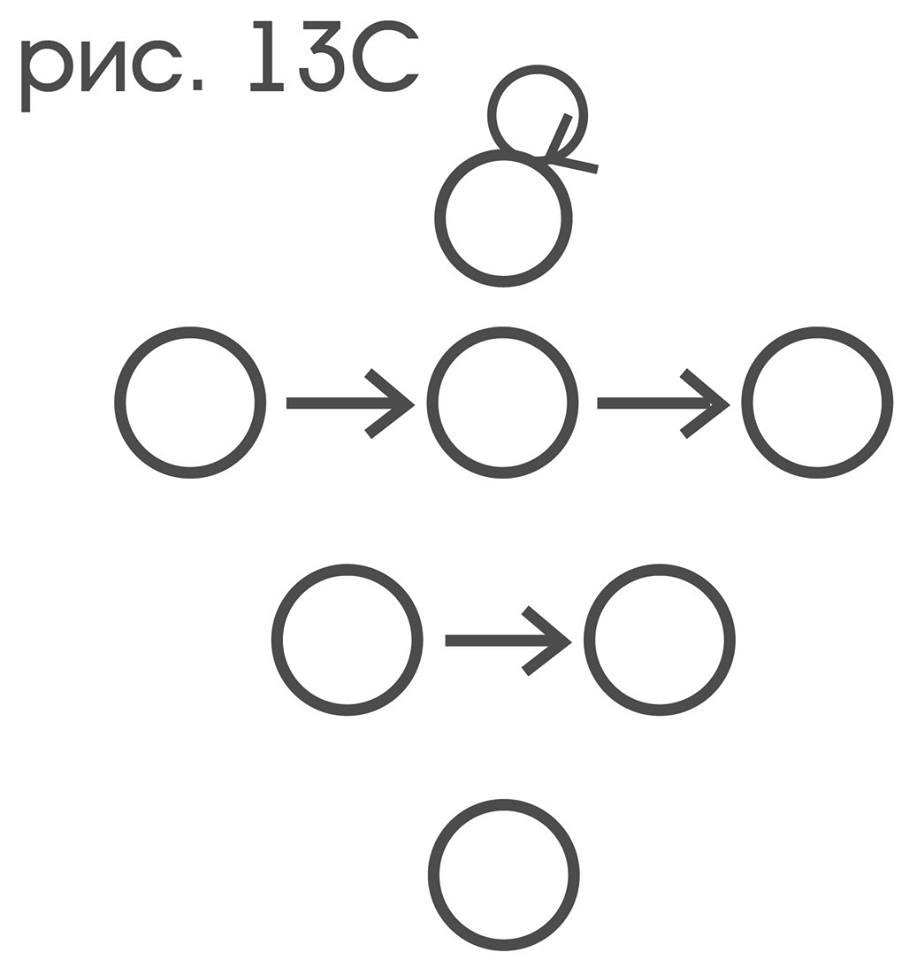
только элементарным поворотам структура R:

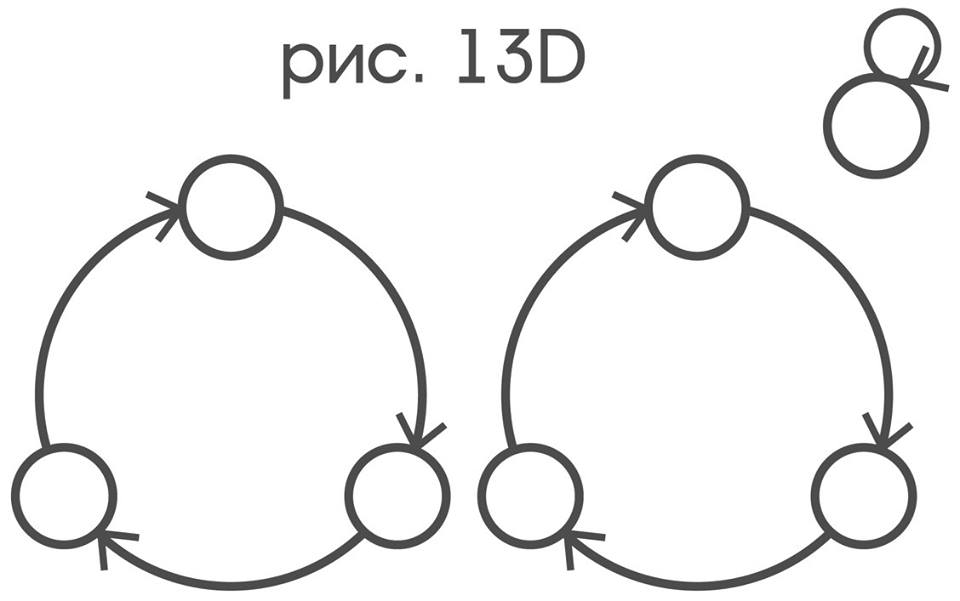
только поворотом на 60° вокруг нецентрального рецептора:

только поворотом на 120° вокруг центрального рецептора:

только тому движению, которое оставляет зонд на месте:


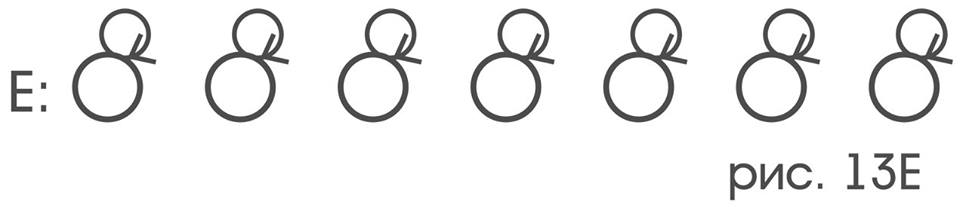
и только движениям, которые переворачивают зонд как монетку, при этом его не смещая

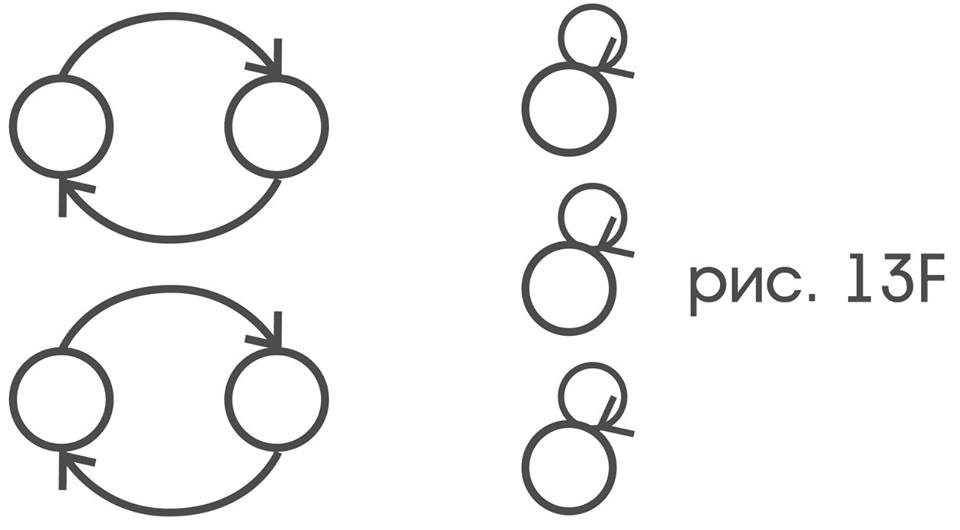
Читателю должно быть очевидно, что если один граф получается из другого простым переименованием вершин, то оба этих графа имеют одинаковую структуру. Именно такой операцией связаны между собой графы двойственных друг к другу отношений, а значит: их структуры должны совпадать. Последние два замечания позволяют даже не имея возможности видеть сам зонд, а исключительно по наблюдению за его индикаторами, для каждого индикатора движений p решить, является ли представляемое им движение элементарным смещением или нет. С этой целью нужно установить, для каких пар x и y цветовых индикаторов выполняется отношение x (p) y и вычертить его граф:p представляет некоторое элементарное смещение в точности тогда, когда получившийся граф имеет структуру S:

Таким образом, фраза «p обладает тем свойством, что граф отношения …(p)… имеет структуру S», если под p понимать движение зонда и остальные термины употреблять в собственном смысле, определяет свойство «быть элементарным смещением», а если термины употреблены в несобственном смысле, двойственное к нему свойство индикатора движения — «представлять элементарное смещение».

Не все рецепторы зонда расположены одинаково друг относительно друга: среди них есть шесть «периферийных» и один «центральный». Существует ли способ, не имея возможности видеть сам зонд, а лишь достаточно долго наблюдая за его индикаторами, определить, какой из индикаторов цвета связан с центральным рецептором, а какие — с периферийными. Чтобы показать существование этого способа, достаточно найти такое категоричное свойство центрального рецептора (как «быть художником»), которое допускало бы перевод в двойственные термины. Этот перевод обязан быть категоричным свойством того индикатора, который связан с центральным рецептором.
Свойство «движению быть элементарным смещением» допускает перевод, свойство «одному рецептору лежать по направлению данного движения от другого рецептора» тоже допускает перевод. По отношению к «центральному» рецептору категоричным будет свойство x: «если движение p – элементарное смещение, то рецептор x как лежит в направлении p от некоторого рецептора, так и некоторый рецептор лежит в направлении p от x”. Последнее выражение, как композиция переводимых, тоже оказывается переводимым.

Часть 2

Сергей Коваленко
Дубна 2015г