В этой статье я начну объяснение того, почему это так, но дам лишь половину доказательства. Эта половина расскажет вам о том, почему существуют КК-партнёры, и почему у всех у них масса M > m. Но эта часть доказательства будет некорректно подразумевать, что для каждой массы M, большей m, существует частица-партнёр. И только на втором шаге, когда мы добавим немного квантовой механики, мы получим правильный ответ: эти частицы обладают дискретным набором определённых масс, в котором первая несколько (возможно, намного) тяжелее известной.
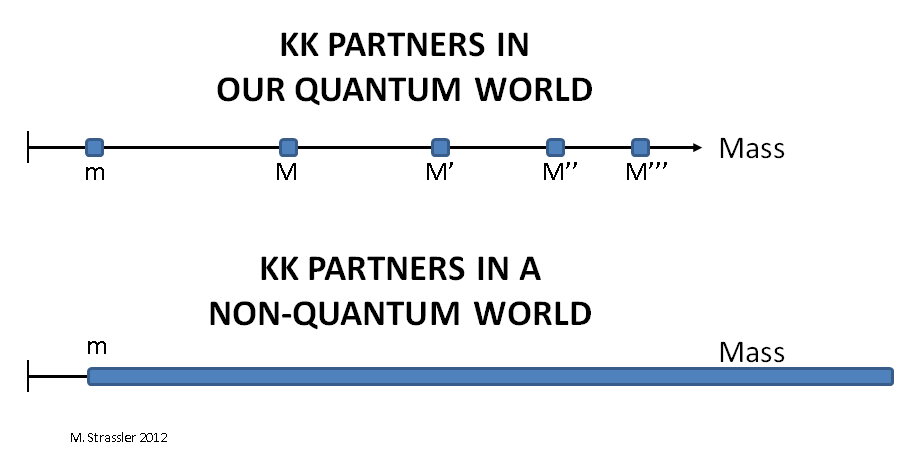
Рис. 1
Начнём с наивного вопроса про полоску — судового канала из наших предыдущих примеров. Такой наблюдатель, как грузовое судно из примера, ничего не знает по поводу короткого измерения, и считает, что канал — это линия, а не полоса. Но если этот наблюдатель обладает научным умом, он сможет кое о чём догадаться. Во-первых, он знает о движении вперёд и назад вдоль полоски; для него имеют смысл скорость и импульс, направленные вдоль неё. Во-вторых, он знает про энергию и про то, что она связана с массой и движением. В частности, энергия частицы E связана с её массой m и движением (в частности, импульсом p вдоль полоски) по известной формуле Эйнштейна:
Она говорит, что энергия частицы задаётся комбинацией энергии массы и энергии движения. Для неподвижной частицы, не имеющей импульса (p = 0) эта формула сводится к E2 = m2 c4, или, иначе говоря, E = m c2.
Так что, если в канале будет без движения находиться небольшая лодка, наблюдатель, которому известны оба измерения, скажет о ней: её импульс нулевой, а энергия получена от массы E = m c2. И наблюдатель, которому известно только про измерение вдоль полоски, скажет то же самое. См. рис. 2, верхнюю треть, где точка зрения наблюдателя, знающего про два измерения, приведена в верхней части, а точка зрения наблюдателя, знающего лишь об одном измерении, указана снизу.
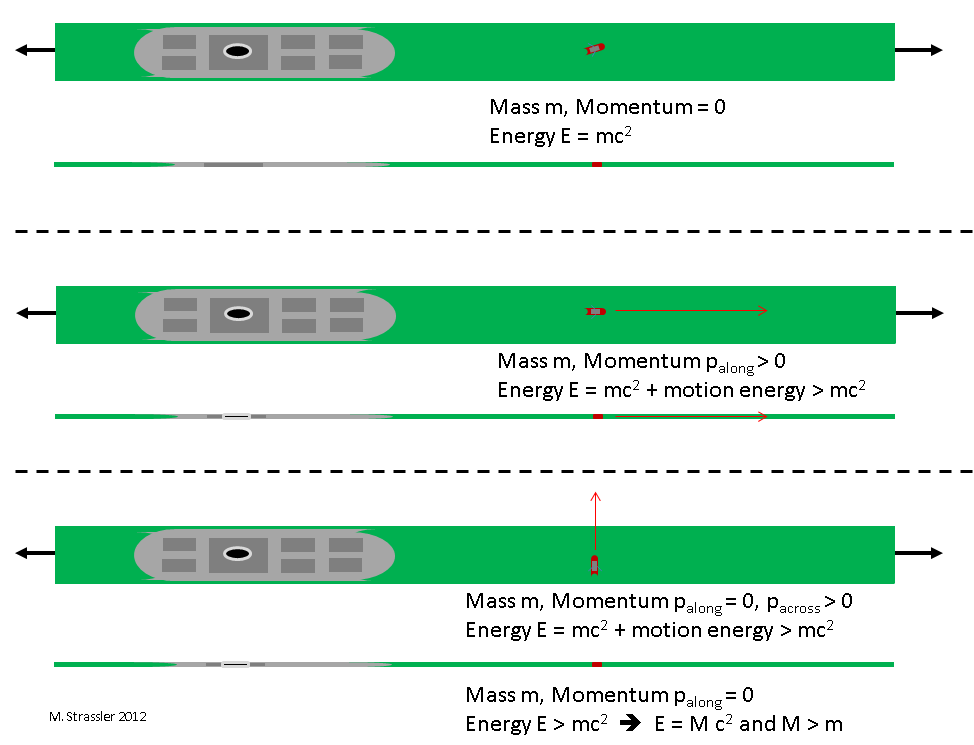
Рис. 2
Если же мелкая лодка движется по каналу, то наблюдатель, имеющий представление об обеих измерениях, скажет: её импульс вдоль канала pвдоль ненулевой, и квадрат её энергии равен
И наблюдатель, знающий только про одно измерение, опять-таки скажет то же самое. См. рис. 2, среднюю часть.
Но что скажет наблюдатель, изучающий частицу, движущуюся не вдоль полоски, а поперёк? См. рис. 2, нижнюю треть.
Наблюдатель, знающий про два измерения, скажет: её импульс вдоль канала pвдоль нулевой, но импульс поперёк канала pпоперёк ненулевой, поэтому квадрат её энергии будет равен
Отметим, что это обязательно означает, что E > m c2, поскольку у лодки есть как энергия массы, так и энергия движения.
Однако наблюдатель, знающий только про одно измерение, не сможет сказать то же самое, поскольку ему ничего неизвестно о возможности pпоперёк. Он подумает, глядя на эту частицу, что она не движется. Она ведь не движется вдоль канала, а только такое движение этот наблюдатель способен уловить. Поэтому, согласно наблюдателю, всю энергию частицы, какой бы она ни была, необходимо отнести на счёт её массы.
Так что глядя на частицу с pвдоль = 0 и ненулевым pпоперёк, одномерный наблюдатель совершает ошибку, хотя и довольно интересную. Он говорит: хмм. Импульс этого объекта равен нулю, поэтому его энергия должна равняться его массе, помноженной на c2, как было в случае с лодкой в верхней части рисунка. Но его энергия E оказывается больше, чем mc2, следовательно это не может быть та же лодка, которую мы видели в верхней части рисунка. Очевидно, в природе есть ещё один тип небольших лодок, о котором мы не знали, похожий на первый, но с другой, большей массой: M = E/c2.
Иначе говоря, если лодка массы m движется с импульсом pпоперёк поперёк канала, наивный наблюдатель ничего не знает про дополнительное измерение, и сделает некорректный вывод о том, что он наблюдает лодку массы M > m, с
Исходя из таких рассуждений мы получаем правильную информацию: признак наличия дополнительного измерения в присутствии частиц, похожих по сути на известные частицы (которые движутся только вдоль полоски), но кажущихся тяжелее (из-за их ненаблюдаемого движения поперёк полоски). Это сразу можно обобщить от случая с полоской (с одним длинным и одним коротким измерениями) на нашу Вселенную (с тремя длинными измерениями и, возможно, с одним или более короткими). Когда известные частицы движутся в дополнительных (неизвестных) измерениях, они кажутся нам более тяжёлыми версиями самих себя.
Но полученная нами по этим данным интуиция тоже неправильная, поскольку из них можно сделать вывод, что частица, движущаяся поперёк полоски, может иметь любой импульс, и следовательно, наблюдатель должен видеть частицы со всеми возможными массами M, превышающими m, как показано внизу рис. 1. А это не так. Вместо этого возможны только определённые значения масс M, как показано вверху рис. 1 — дискретный набор, не непрерывное множество частиц, которое следовало бы из наших рассуждений. Всё из-за квантовой механики. Из-за того, что «частицы» на самом деле представляют собой квантующиеся волны, кванты, что не выполнялось для маленькой лодки из нашего примера. В следующей статье мы увидим, откуда появляется такая разница.
Комментарии (21)

eggstream
03.01.2018 18:35Забавно. А что мешает нам пойти в рассуждениях дальше и принять, что массы как таковой не существует, а есть только энергия, содержащаяся в импульсах по ненаблюдаемым нами измерениям?

Tyusha
04.01.2018 01:04Отвечу в духе photino: уже давно пошли. ru.m.wikipedia.org/wiki/Теория_струн

eggstream
04.01.2018 11:33Тогда еще несколько наивных вопросов:
1. Торможение частицы, двигающейся строго по ненаблюдаемой нами оси должно давать тормозное излучение на визуально неподвижной частице. Наблюдаем ли мы такое?
2. Проекции нескольких частиц могут давать полное или частичное перекрытие и визуально давать странные эффекты вплоть до визуального нарушения принципов запрета. Наблюдаем ли мы такое?
3. Движение заряженной частицы строго по ненаблюдаемой нами оси должно вызывать кучу электромагнитных эффектов при якобы покоящейся частице. Наблюдаем ли мы такое?
Tyusha
04.01.2018 12:46Вижу вы не совсем понимаете, как выглядят дополнительные измерения. Они свёрнуты до субатомных масштабов. Представьте себе длинную тонкую трубку — это будет одно «наше» и одно дополнительное скрытое измерение. Частица может двигаться прямо по поверхности трубы (вдоль образующей), это будет обычная частица. А может двигаться по винтовой линии. Это и есть частица более высокой массы, т.к. часть её массы это энергия движения «по кругу» в скрытом измерении, которое мы не видим.
Теперь к вашим вопросам:
1. Не поняла, что за тормозное излучение. Движущаяся только вдоль скрытой оси частица просто наматывает круги, с нашей же точки зрения она стоит на месте. И другая частица стоит на месте. Никакого излучения.
2. Два одинаковых фермиона, даже находящиеся в одной точке пространства могут иметь разные импульсы в направлении скрытого измерения. Т. е. они находятся в разных состояниях, и принцип Паули не нарушается.
3. Электромагнитные эффекты порождённые в экстра-измерениях заперты в них как в волноводе. Хотя на микроуровне дополнительного измерения закон Кулона изменяет свою степень, и там конечно весь электромагнетизм другой. Снаружи та куча эффектов, о которой вы пишите, проявляется в виде тяжёлых векторных бозонов вместо фотонов, т.к. испущенные «под углом» они в проекции на наше измерение имеют скорость очевидно меньше световой и приобретают массу по тем же причинам.

eggstream
04.01.2018 15:35Я понимаю, что речь идет не о полноценном измерении, как три наших привычных пространственных. Но если масштаб этого измерения позволяет на дополнительной оси разместить «в ряд» или «по ободу» — неважно как несколько частиц, то для моих вопросов выходит все равно являются ли дополнительные измерения бесконечными или конечными, свёрнутыми.
1. По тормозному излучению. Возможно, я выразил мысль недостаточно точно, я не физик. Допустим, у нас имеется некое электрическое поле. В нем неподвижно для трехмерного наблюдателя находится некая заряженная частица, например электрон. Но на самом деле она движется относительно дополнительного измерения. Затем по какой-то причине, например из-за столкновения с другой частицей, этот электрон останавливается. По идее, мы должны получить некое тормозное излучение, как в рентгеновском аппарате. Насколько я понял из вашего ответа на мой вопрос №3, там вполне может возникнуть любое излучение, но оно будет заперто в этом измерении или проявит себя какими-то странными бозонами, так? А появление таких, казалось бы спонтанных, бозонов встречается на практике?
Tyusha
04.01.2018 23:38Если рассмотреть под микроскопом заряд в пространстве 3+1 (не считая времени), то мы увидим закон Купона вида 1/r^3. Причём в наших измерениях на масштабе больше размера свёрнутрго измерения попрежнемубудет 1/r^2.
Тот процесс, который вы предлагаете, снаружи будет выглядеть так. Массивная заряженная частица M превращается в более лёгкую m, испустив тяжёлый векторный бозон.

eggstream
05.01.2018 00:11Ага, то есть с наблюдениями эта теория всё-таки согласовуется. Хорошо. А если у нас будет движение частицы одновременно в наших 3 измерениях и в дополнительных, то излучится одновременно тяжелый бозон и фотон или это будет какой-то бозон средней тяжести?
Кстати, еще один вопрос появился. Уравнения, описывающие рассеяние света (подозреваю, что и для других частиц похоже), завязаны на телесный угол в трех измерениях и дополнительных не учитывают. Этому тоже есть объянение?
Tyusha
05.01.2018 15:17Ох… «Под микроскопом» в переносном смысле и вообще умозрительное рассуждение, не имеющее отношения к опыту. Т.е. (везде дальше для простоты одно большое измерение и одно скрытое) когда мы маленькие муравьи на поверхности трубы 1+1 мы видим плоскость — полноценное двухмерие, а если мы люди, то в то же самом видим одномерную трубу, и то что это труба, а не нить, мы можем узнать только за счёт дополнительных экспериментов, например регистрировать частицы-партнёры, о которых статья. На истинно одномерной нити таких партнёров быть не может.
Если муравей рассмотрит остановку частицы, то он увидит, что частица никак сама по себе не изменилась, а просто отклонилась, и при этом излучился безмассовый фотон в своих двух измерениях, а для нас то же самое будет выглядеть как превращение сорта частицы и излучение массивного бозона в нашем одном измерении.
JohnSmith001
03.01.2018 19:02А где примеры частиц-партнеров? Их нет, насколько я понимаю?

Tyusha
04.01.2018 01:12Да, к сожалению акты на такие частицы пылится в бухгалтерии ЦЕРНа незакрытыми. Нужны новая смета и новый бюджет.

photino
04.01.2018 19:12Как это ни странно, их действительно искали — есть довольно много статей от коллабораций с анализом данных по поиску Калуца-Клейновских мод. Но ничего не нашли.

Tyusha
04.01.2018 13:14На материале этой статьи можно даже пояснить, что такое проблема ландшафта в теории струн. Если у нас одно свёрнутое измерение — оно кольцо. Если два, то они уже имеют форму тора (кольцо намотанное на кольце). Тут пока всё однозначно. Если же добавить третье свёрнутое измерение, то во-первых эту форму уже не представить визуально, а во-вторых появляются варианты, в каком порядке три кольца наматывать друг на друга, полученные трёхмерные пространства будут иметь разную топологии. Если же перейти к 7 свёрнутым измерениям теории струн, то там настолько всё сложно становится, что даже классифицировать пространства пока не удаётся. Они называются пространствами Калаби-Яу.
При 7 измерениях даже не понятно, сколько таких пространств возможно. Но в любом случае количество способов скрутить 7 измерений рвёт мозг. Считается, что их то-ли 10^100 то-ли 10^500. А между тем вся физика и весь спектр частиц и взаимодействия сводится в теории струн к выбору нужного пространства Калаби-Яу. А среди их числа всегда найдётся такое, которое объяснит наш мир… и любой другой. Т. е. теория полностью теряет предсказательную силу, т. к. есть козырь на любой наблюдаемый эффект. И это проблема. Такая теория становится нефальсифицируемой, божественной, её нельзя опровергнуть в принципе ничем, притом что ничего полезного она не несёт.
В контексте данной статьи можно сказать, что спектр масс M', M" зависит от способа свёртки дополнительных измерений.


photino
К сожалению, очень часто при написании научно-популярных статей ради упрощения либо что-то важное упускают, либо приводят аналогии, которые не соответствуют реальному положению вещей. В общем, вместе с водой выплескивают и ребенка, но у людей, не разбирающихся в вопросе, возникает иллюзия понимания. Вот и у Страсслера написано
Квантовая механика здесь если и виновата, то косвенно. Эффект возникает из-за компактности дополнительного измерения. Если поместить в пятимерное (время + 3 наши пространственные координаты + компактное дополнительное измерение) классическое электромагнитное поле, то на выходе будем иметь обычные уравнения Максвелла плюс уравнения, описывающие бесконечный набор массивных (с четырехмерной точки зрения) векторных полей. Это происходит потому, что в дополнительном измерении пятимерное поле должно иметь (в простейшем случае) периодические граничные условия, это поле можно разложить в ряд Фурье по координате дополнительного измерения (опять же, в простейшем случае это ряд Фурье, в более сложных случаях наборы собственных функций удобнее выбрать другими). В результате поля, соответствующие гармоникам, будут подчиняться уравнениям, описывающим четырехмерные массивные поля.
Естественно, поместив любое классическое поле в такое пятимерное пространство, получим аналогичный эффект. А вот чтобы описать частицы, нужно эти поля проквантовать, так как именно квантованные поля описывают частицы. То есть эффект дискретности масс в теории с компактным дополнительным измерением возникает не из-за того, что есть реально точечная частица, которая по каким-то причинам не может иметь непрерывный спектр импульса в дополнительном измерении, а потому, что частица описывается с помощью полей, а даже для классических полей дополнительное измерение приводит к квантованию (в смысле дискретизации, а не в смысле отношения к квантовой механике) их импульса (для классических полей тоже можно определить понятие импульса).
Скорее, тут можно привести аналогию с колебаниями закрепленной струны: основной тон — низшая мода, обертоны — Калуца-Клейновские возбуждения.
квантованные
wych-elm
Вот, у нас есть различные поля в пространстве и фактически каждое из них можно квантовать, а почему никто не предположил что возможность квантования полей — это не свойство полей, а свойство самого пространства в котором они находятся. То есть, почему считается что пространство не квантуется? Или я чего-то не понимаю?
photino
Уже давно предположили: Петлевая квантовая гравитация
Tyusha
Стоит отметить, что сегодня «кватование» как таковое есть некая более широкая процедура, нежели построение теории волны-частицы, как это было в начале 20 века. И даже пространство-время может оказаться непричём. Можно формально попытать построить квантовую, чёрт её дери, социологию. Выбрав какую-то модель, которая будет отвечать пяти квантовым постулатам.
Т. е. квантовая теория это сегодня некий математический тип теории, которая сама по себе может быть о чём угодно.
Я вам больше скажу. Существуют разные способы квантовая одного и того же. Кроме того теперь строят изначально квантовые теории без классической аналога.