
Введение
Эта публикация дает простое и интуитивно понятное введение к вопросу об использовании фильтра Калмана. Публикация рассчитана на тех, кто слышал о фильтре Калмана, но не знает, как он работает, а также на тех, кто знает уравнения фильтра Калмана, но не знает, откуда они берутся.
Требуемые знания: знакомство с матричной алгеброй, нормальным многомерным распределением, ковариацией матриц и т. д.
Постановка задачи
Фильтр Калмана имеет множество применений в технике и экономике. Выберем не тривиальную задачу – отслеживание местоположения ракеты запущенyой из страны Y. Обозначим текущее местоположение ракеты
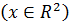 как пару координат широты – a и долготы – b, на контурной карте это
как пару координат широты – a и долготы – b, на контурной карте это 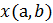 .
.На данный момент времени, точные координаты х неизвестны, но мы можем определить вероятность нахождения ракеты в данной точке
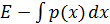 исходя из двумерной плотности вероятности
исходя из двумерной плотности вероятности 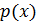 . Предполагая гауссовским закон распределения, значение плотности вероятности в точке можно записать в виде:
. Предполагая гауссовским закон распределения, значение плотности вероятности в точке можно записать в виде: (1)
(1)где:
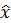 — распределение вероятности местоположения ракеты;
— распределение вероятности местоположения ракеты;? – ковариационная матрица 2?2.
В рассматриваемой модели:
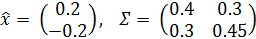 (2)
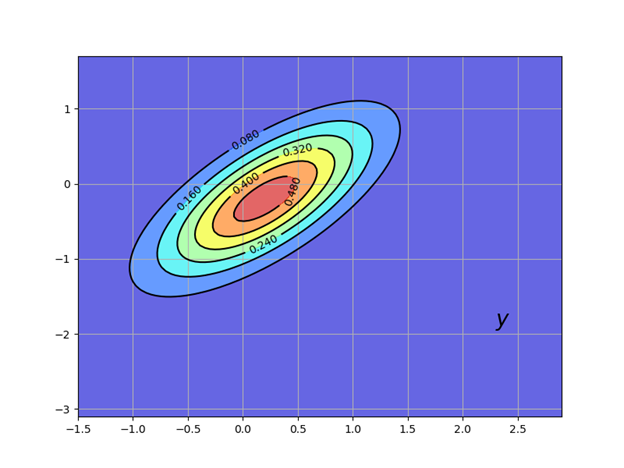
(2)Используем следующий листинг для построения на плоскости эллиптической области распределения вероятности с центром красного цвета.
Листинг решения
from scipy import linalg
import numpy as np
import matplotlib.cm as cm
from matplotlib.mlab import bivariate_normal
import matplotlib.pyplot as plt
# == Настройка гостовской плотности р == #
? = [[0.4, 0.3], [0.3, 0.45]]
? = np.matrix(?)
x_hat = np.matrix([0.2, -0.2]).T
# ==Определим матрицы G и R из уравнения y = G x + N(0, R) == #
G = [[1, 0], [0, 1]]
G = np.matrix(G)
R = 0.5 * ?
# == Матрицы A и Q== #
A = [[1.2, 0], [0, -0.2]]
A = np.matrix(A)
Q = 0.3 * ?
# == Матрицы A и Q == #
y = np.matrix([2.3, -1.9]).T
# == Настройка сетки для построения графика== #
x_grid = np.linspace(-1.5, 2.9, 100)
y_grid = np.linspace(-3.1, 1.7, 100)
X, Y = np.meshgrid(x_grid, y_grid)
def gen_gaussian_plot_vals(?, C):
"µTorrent.lnk "
m_x, m_y = float(?[0]), float(?[1])
s_x, s_y = np.sqrt(C[0, 0]), np.sqrt(C[1, 1])
s_xy = C[0, 1]
return bivariate_normal(X, Y, s_x, s_y, m_x, m_y, s_xy)
#Построить график
fig, ax = plt.subplots(figsize=(8,6))
ax.grid()
Z = gen_gaussian_plot_vals(x_hat, ?)
ax.contourf(X, Y, Z, 6, alpha=0.6, cmap=cm.jet)
cs = ax.contour(X, Y, Z, 6, colors="black")
ax.clabel(cs, inline=1, fontsize=10)
plt.show()Получим:

Определение шага фильтрации
Датчики, установленные на ракете, сообщают координаты её текущего положения
 . Поместим эту точку на график с помощью следующего листинга.
. Поместим эту точку на график с помощью следующего листинга.Листинг решения
fig, ax = plt.subplots(figsize=(8, 6))
ax.grid()
Z = gen_gaussian_plot_vals(x_hat, ?)
ax.contourf(X, Y, Z, 6, alpha=0.6, cmap=cm.jet)
cs = ax.contour(X, Y, Z, 6, colors="black")
ax.clabel(cs, inline=1, fontsize=10)
ax.text(float(y[0]), float(y[1]), "$y$", fontsize=20, color="black")
plt.show()Получим:
Датчики неточны поэтому мы должны интерпретировать выход нашего датчика не как
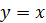 , а следующим образом:
, а следующим образом: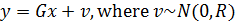 (3)
(3)Здесь матрицы G и R имеют размерность 2?2, а матрица R содержит только положительные элементы. Помеха в виде шумов –
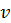 , не зависит от измеряемых координат –
, не зависит от измеряемых координат –  .
.Для объединения плотности вероятности
 и полученного соотношения для y воспользуемся уравнением Байеса используя безусловную
и полученного соотношения для y воспользуемся уравнением Байеса используя безусловную 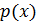 и условную
и условную 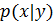 вероятности:
вероятности:
где:

Для определения
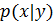 воспользуемся следующими соотношениями и условиями:
воспользуемся следующими соотношениями и условиями: ;
;- с учётом соотношения (3), относительная вероятность
 равна
равна 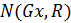 ;
; 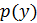 не зависит от
не зависит от  и входит в вычисления только как нормализующая постоянная.
и входит в вычисления только как нормализующая постоянная.
Поскольку мы находимся в линейной и гауссовой структуре, обновленная плотность может быть вычислена путем вычисления линейных регрессий; в частности, известно решение [1]:
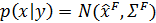
где:
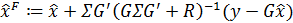
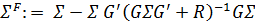 (4)
(4)где:
 — матрица коэффициентов регрессии.
— матрица коэффициентов регрессии.Эта новая плотность
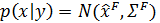 показана на следующем рисунке через контурные линии и цветовую карту. Первоначальная плотность оставлена в виде контурных линий для сравнения.
показана на следующем рисунке через контурные линии и цветовую карту. Первоначальная плотность оставлена в виде контурных линий для сравнения.Листинг решения
fig, ax = plt.subplots(figsize=(8, 6))
ax.grid()
Z = gen_gaussian_plot_vals(x_hat, ?)
cs1 = ax.contour(X, Y, Z, 6, colors="black")
ax.clabel(cs1, inline=1, fontsize=10)
M = ? * G.T * linalg.inv(G * ? * G.T + R)
x_hat_F = x_hat + M * (y - G * x_hat)
?_F = ? - M * G * ?
new_Z = gen_gaussian_plot_vals(x_hat_F, ?_F)
cs2 = ax.contour(X, Y, new_Z, 6, colors="black")
ax.clabel(cs2, inline=1, fontsize=10)
ax.contourf(X, Y, new_Z, 6, alpha=0.6, cmap=cm.jet)
ax.text(float(y[0]), float(y[1]), "$y$", fontsize=20, color="black")
plt.show()Получим:

Наша новая плотность «закручивает» предыдущую
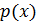 в направлении, определяемом новой информацией
в направлении, определяемом новой информацией  .
.При генерации фигуры мы устанавливаем G как единичную матрицу и

, матрица для
 согласно соотношению (2).
согласно соотношению (2).Прогноз на шаг вперёд
Подведём промежуточные итоги. Нами получено вероятное текущее положение ракеты с использованием информации о начальном и текущем её положении. Это имеет название фильтрация, но не прогнозирование, поскольку фильтруем от шума, но не можем предсказать местоположение ракеты в следующий момент времени.
Давайте предположим, что нам поставлена другая задача: предсказать местоположение ракеты после истечения единицы времени, не имея никакой информации о новом её местоположении.
Для решения этой задачи используем линейную гауссовою модель вида:
 (5)
(5)Наша цель – объединить этот закон движения и наше текущее распределение
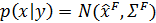 , чтобы придумать новое предсказательное распределение для местоположения ракеты за одну единицу времени.
, чтобы придумать новое предсказательное распределение для местоположения ракеты за одну единицу времени.Ввиду (5) все, что нам нужно сделать, – ввести случайный вектор
 и выработать распределение
и выработать распределение  , где w не зависит от
, где w не зависит от  и имеет распределение
и имеет распределение 
Поскольку в (5) используются линейные комбинации случайных переменных с гауссовыми распределениями, то и
 также является гауссовой переменной.
также является гауссовой переменной.После преобразований соотношений (4) с учётом введенных переменных получим:


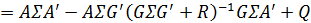
Матрица
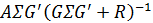 часто записывается как
часто записывается как  и называется усилением Кальмана. Добавлен индекс
и называется усилением Кальмана. Добавлен индекс  , напоминающий нам, что
, напоминающий нам, что  зависит от
зависит от  , но не зависит от
, но не зависит от 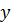 или
или 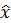
Используя эти обозначения, мы можем суммировать наши результаты следующим образом. Наше обновленное предсказание – имеет плотность вероятности
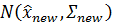 , где:
, где:
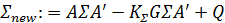 (6)
(6)Плотность
 называется прогностическим распределением. Прогностическое распределение – это новая плотность, показанная на следующем рисунке, где использованы обновлённые параметры:
называется прогностическим распределением. Прогностическое распределение – это новая плотность, показанная на следующем рисунке, где использованы обновлённые параметры: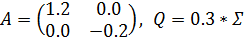
Листинг решения
fig, ax = plt.subplots(figsize=(8,6))
ax.grid()
# Плотность 1
Z = gen_gaussian_plot_vals(x_hat, ?)
cs1 = ax.contour(X, Y, Z, 6, colors="black")
ax.clabel(cs1, inline=1, fontsize=10)
# Плотность 2
M = ? * G.T * linalg.inv(G * ? * G.T + R)
x_hat_F = x_hat + M * (y - G * x_hat)
?_F = ? - M * G * ?
Z_F = gen_gaussian_plot_vals(x_hat_F, ?_F)
cs2 = ax.contour(X, Y, Z_F, 6, colors="black")
ax.clabel(cs2, inline=1, fontsize=10)
# Плотность 3
new_x_hat = A * x_hat_F
new_? = A * ?_F * A.T + Q
new_Z = gen_gaussian_plot_vals(new_x_hat, new_?)
cs3 = ax.contour(X, Y, new_Z, 6, colors="black")
ax.clabel(cs3, inline=1, fontsize=10)
ax.contourf(X, Y, new_Z, 6, alpha=0.6, cmap=cm.jet)
ax.text(float(y[0]), float(y[1]), "$y$", fontsize=20, color="black")
plt.show()Получим:
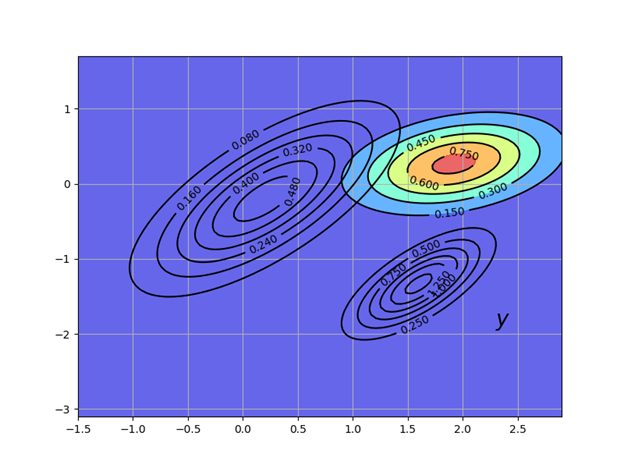
Рекурсивная процедура
Давайте посмотрим на то, что мы сделали. Мы начали текущий период с
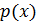 для размещения координат
для размещения координат  ракеты. Затем мы использовали текущее измерение для обновления вероятности до. Наконец, мы использовали закон движения (5) для
ракеты. Затем мы использовали текущее измерение для обновления вероятности до. Наконец, мы использовали закон движения (5) для 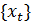 обновить до
обновить до 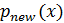 .
.Если мы сейчас переходим к следующему периоду, мы снова готовы взять
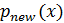 в качестве предшествующего периода. Обозначая
в качестве предшествующего периода. Обозначая 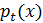 для
для 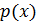 и
и  для
для 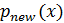 , полная рекурсивная процедура состоит:
, полная рекурсивная процедура состоит:- Начинаем текущий период с предшествующего
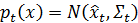
- Получаем текущее измерение
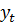
- Вычислить распределение фильтрации
 из
из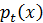 и
и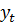 , применяя правило Байеса и условное распределение (3) ;
, применяя правило Байеса и условное распределение (3) ; - Вычислить прогностическое распределение
 из фильтрационного распределения (5);
из фильтрационного распределения (5); - Приращение t на единицу и переход к шагу 1.
Повторяя (6), динамика для
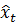 и
и  выглядит следующим образом:
выглядит следующим образом:
 (7)
(7)Это стандартные динамические уравнения для фильтра Калмана (см., например, [2], с. 58)
Конвергенция
Матрицa
 является мерой неопределенности нашего предсказания
является мерой неопределенности нашего предсказания 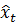 из
из 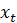 . Помимо особых случаев, эта неопределенность никогда не будет полностью решена, независимо от того, сколько времени истекает.
. Помимо особых случаев, эта неопределенность никогда не будет полностью решена, независимо от того, сколько времени истекает.Одна из причин заключается в том, что наше предсказание
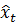 составлено на основе информации, доступной в t-1, а не t. Даже если мы знаем точное значение
составлено на основе информации, доступной в t-1, а не t. Даже если мы знаем точное значение  (чего мы не делаем), из уравнения перехода (5) следует, что:
(чего мы не делаем), из уравнения перехода (5) следует, что:
Поскольку
 не наблюдается при t-1, в любое время предсказание
не наблюдается при t-1, в любое время предсказание 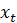 повлечет за собой некоторую ошибку (если
повлечет за собой некоторую ошибку (если  не вырождается).
не вырождается).Однако, конечно, возможно, что
 сходится к постоянной матрице при
сходится к постоянной матрице при  . Чтобы изучить эту тему, давайте разберем второе уравнение в (7):
. Чтобы изучить эту тему, давайте разберем второе уравнение в (7): (8)
(8)Это нелинейное разностное уравнение для
 . Фиксированная точка (8) является постоянной матрицей ? такой, что:
. Фиксированная точка (8) является постоянной матрицей ? такой, что: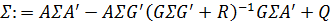
Уравнение (8) известно, как разностное уравнение Риккати дискретного времени. Уравнение (9) называется дискретным временным алгебраическим уравнением Риккати.
Условия, при которых существует неподвижная точка и сходящаяся к ней последовательность
 , обсуждаются в [3] и [4], глава 4.
, обсуждаются в [3] и [4], глава 4.Достаточным (но не необходимым) условием является то, что все собственные значения
 матрицы A удовлетворяют
матрицы A удовлетворяют  (см., например, [4], стр. 77). Это сильное условие гарантирует, что безусловное распределение
(см., например, [4], стр. 77). Это сильное условие гарантирует, что безусловное распределение 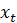 сходится при
сходится при 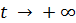 .
.В этом случае для любого начального выбора
 , неотрицательного и симметричного, последовательность
, неотрицательного и симметричного, последовательность  в (8) сходится к неотрицательной симметрической матрице
в (8) сходится к неотрицательной симметрической матрице  , которая является решением (9).
, которая является решением (9).Реализация
Класс Kalman из пакета QuantEcon.py реализует фильтр Kalman на основе линейной модели пространства состояний следующего вида:
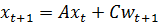

Приведём переход переменных к принятым в публикации обозначениям:
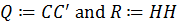
Класс Kalman из пакета QuantEcon.py [5] имеет ряд методов, приведём те, которые относятся к данной публикации:
- before_to_filtered, метод обновляет
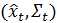 до
до  ;
; - filter_to_forecast, метод обновляет распределение фильтрации до прогнозирующего распределения – которое становится новым ранее
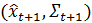 ;
; - update, обновление, которое сочетает в себе последние два метода;
- stationary_values, метод вычисляет решение уравнения (9) и соответствующее (стационарное) усиление Кальмана.
Примеры использования класса Kalman из пакета QuantEcon.py
Пример 1
Рассмотрим следующее простое применение фильтра Калмана взятое из [2], раздел 2.9.2. Предположим, что все переменные являются скалярами, скрытое состояние
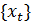 фактически является постоянным, равным некоторому значению
фактически является постоянным, равным некоторому значению  . Динамика состояний отражена в выражении (5) с
. Динамика состояний отражена в выражении (5) с ,
,  и
и 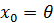 . Уравнение измерения:
. Уравнение измерения:  , где
, где  равно
равно  .
.Задача этого примера с использованием kalman.py построить первые пять предсказательных плотностей
 . При моделировании использовать следующие значения переменных
. При моделировании использовать следующие значения переменных 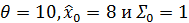 .
.Листинг решения
from quantecon import Kalman
import numpy as np
from quantecon import LinearStateSpace
import matplotlib.pyplot as plt
from scipy.stats import norm
# == параметры == #
? = 10 # Постоянное значение состояния x_t
A, C, G, H = 1, 0, 1, 1
ss = LinearStateSpace(A, C, G, H, mu_0=?)
# ==задание до инициализации фильтра Калмана == #
x_hat_0, ?_0 = 8, 1
kalman = Kalman(ss, x_hat_0, ?_0)
# == наблюдение за измерением в модели пространства состояний== #
N = 5
x, y = ss.simulate(N)
y = y.flatten()
# == настроить график == #
fig, ax = plt.subplots(figsize=(8,6))
xgrid = np.linspace(? - 5, ? + 2, 200)
for i in range(N):
# == записать текущее прогнозируемое среднее и дисперсию== #
m, v = [float(z) for z in (kalman.x_hat, kalman.Sigma)]
# =обновление фильтра == #
ax.plot(xgrid, norm.pdf(xgrid, loc=m, scale=np.sqrt(v)), label=f'$t={i}$')
kalman.update(y[i])
ax.set_title(f'Первые {N} распределений плотности вероятности \n при $\\theta = {?:.1f}$')
ax.legend(loc='upper left')
plt.show()Получим:

Как показано в [2], в разделах 2.9.1-2.9.2, эти распределения асимптотически приближаются к неизвестному значению
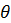 .
.Пример 2
На предыдущем графике приведена некоторая поддержка идеи о том, что интеграл плотности вероятности сходится к
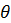 .
.Чтобы проверить идею, нужно выбрать небольшое
 и вычислить интеграл:
и вычислить интеграл:
для
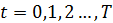 .
.Листинг решения
from quantecon import Kalman
from numpy import*
from quantecon import LinearStateSpace
from scipy.stats import norm
import matplotlib.pyplot as plt
from scipy.integrate import quad
? = 0.1
? = 10 # Постоянное значение состояния x_t
A, C, G, H = 1, 0, 1, 1
ss = LinearStateSpace(A, C, G, H, mu_0=?)
x_hat_0, ?_0 = 8, 1
kalman = Kalman(ss, x_hat_0, ?_0)
T = 600
z = empty(T)
x, y = ss.simulate(T)
y = y.flatten()
for t in range(T):
# Запись текущего предсказанного среднего, дисперсии их плотности распределения
m, v = [float(temp) for temp in (kalman.x_hat, kalman.Sigma)]
f = lambda x: norm.pdf(x, loc=m, scale=sqrt(v))
integral, error = quad(f, ? - ?, ? + ?)
z[t] = 1 - integral
kalman.update(y[t])
fig, ax = plt.subplots(figsize=(8, 6))
ax.set_ylim(0, 1)
ax.set_xlim(0, T)
ax.plot(range(T), z)
ax.fill_between(range(T), zeros(T), z, color="blue", alpha=0.2)
plt.show()Получим:
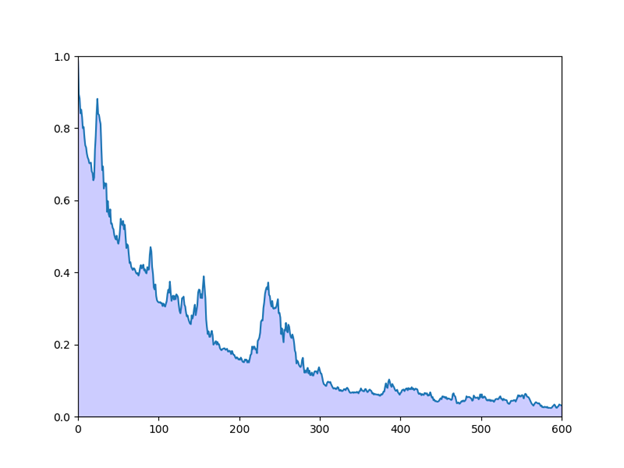
Пример 3
Как обсуждалось выше, последовательность
 не вырождена, то в общем случае невозможно предсказать
не вырождена, то в общем случае невозможно предсказать 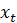 без ошибок в момент времени t-1 (и это было бы так, даже если бы мы могли наблюдать
без ошибок в момент времени t-1 (и это было бы так, даже если бы мы могли наблюдать  ). Давайте теперь сравним предсказание
). Давайте теперь сравним предсказание 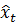 , сделанное фильтром Калмана, против конкурента, которому разрешено наблюдать
, сделанное фильтром Калмана, против конкурента, которому разрешено наблюдать  .
.Этот конкурент будет использовать условное ожидание
 , которое в этом случае является
, которое в этом случае является 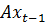 .. Известно, что условное ожидание является оптимальным методом прогнозирования с точки зрения минимизации среднеквадратической ошибки. (Точнее, минимизатор
.. Известно, что условное ожидание является оптимальным методом прогнозирования с точки зрения минимизации среднеквадратической ошибки. (Точнее, минимизатор  по g равен
по g равен  ).
).Таким образом, мы сравниваем фильтр Калмана с конкурентом, который имеет больше информации (в смысле возможности наблюдать скрытое состояние) и ведет себя оптимально с точки зрения минимизации квадратичной ошибки. Наши переходы будут оцениваться по квадрату ошибки.
В частности, ваша задача состоит в том, чтобы генерировать график, отображающий наблюдения как
 , так и
, так и  против t при t=1,...,50.
против t при t=1,...,50.Для параметров задайте
 ,
, 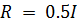 и
и 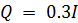 , где I — тождество 2 ? 2.
, где I — тождество 2 ? 2.Задать
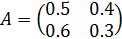 .
.Чтобы инициализировать предыдущую плотность, следует установить:
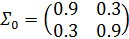 .
.и
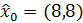 .
.Наконец, установите
 .
.Листинг решения
from scipy.linalg import eigvals
from quantecon import Kalman
import numpy as np
from quantecon import LinearStateSpace
import matplotlib.pyplot as plt
# === Определение A, C, G, H === #
G = np.identity(2)
H = np.sqrt(0.5) * np.identity(2)
A = [[0.5, 0.4],
[0.6, 0.3]]
C = np.sqrt(0.3) * np.identity(2)
# === Настроить модель пространства состояний, начальное значение x_0 установить на ноль=== #
ss = LinearStateSpace(A, C, G, H, mu_0 = np.zeros(2))
# === Определить предыдущую плотность=== #
? = [[0.9, 0.3],
[0.3, 0.9]]
? = np.array(?)
x_hat = np.array([8, 8])
# === Инициализировать фильтр Калмана === #
kn = Kalman(ss, x_hat, ?)
# == Печатать собственные значения A == #
print("Собственные значения A:")
print(eigvals(A))
# == Печать стационарная ?== #
S, K = kn.stationary_values()
print("Дисперсия ошибки стационарного прогноза:")
print(S)
# === Создать сюжет=== #
T = 50
x, y = ss.simulate(T)
e1 = np.empty(T-1)
e2 = np.empty(T-1)
for t in range(1, T):
kn.update(y[:,t])
e1[t-1] = np.sum((x[:, t] - kn.x_hat.flatten())**2)
e2[t-1] = np.sum((x[:, t] - A @ x[:, t-1])**2)
fig, ax = plt.subplots(figsize=(9,6))
ax.plot(range(1, T), e1, 'k-', lw=2, alpha=0.6, label='Ошибка фильтра Калмана')
ax.plot(range(1, T), e2, 'g-', lw=2, alpha=0.6, label='Условная математическая ошибка')
ax.legend()
plt.show()Получим:
Собственные значения A:
[ 0.9+0.j -0.1+0.j]
Дисперсия ошибки стационарного прогноза:
[[0.40329108 0.1050718 ]
[0.1050718 0.41061709]]

Пример 4
Попробуйте изменить коэффициент 0.3 в Q=0.3I вверх и вниз. Для Q=0.5I получим:
Собственные значения A:
[ 0.9+0.j -0.1+0.j]
Дисперсия ошибки стационарного прогноза:
[[0.62286148 0.12527948]
[0.12527948 0.63270989]]

Для Q=0.1I получим:
Собственные значения A:
[ 0.9+0.j -0.1+0.j]
Дисперсия ошибки стационарного прогноза:
[[0.16433113 0.06508848]
[0.06508848 0.16752408]]

Заметим, как диагональные значения в стационарном решении
 (см. (9)) возрастают и убывают в соответствии с этим коэффициентом.
(см. (9)) возрастают и убывают в соответствии с этим коэффициентом.Интерпретация заключается в том, что большая случайность в законе движения для приводит к большей (постоянной) неопределенности в прогнозировании.
- C. M. Bishop. Pattern Recognition and Machine Learning. Springer, 2006.
- L Ljungqvist and T J Sargent. Recursive Macroeconomic Theory. MIT Press, 4 edition, 2018.
- E. W. Anderson, L. P. Hansen, E. R. McGrattan, and T. J. Sargent. Mechanics of Forming and Estimating Dynamic Linear Economies. In Handbook of Computational Economics. Elsevier, vol 1 edition, 1996.
- D. B. O. Anderson and J. B. Moore. Optimal Filtering. Dover Publications, 2005.
- kalman.py.https://github.com/QuantEcon/QuantEcon.py/blob/master/quantecon/kalman.py


Beaglz
Еще про прикладную магию Калмана посредством Excel можно почитать здесь
www.mathfinance.cn/kalman-filter-example