Исходя из этого, возникает задача первичной обработки информации в ИИК – фильтрация сигнала y(t) измерительной информации от случайной помехи e(t). В основном, методы фильтрации основаны на различии частотных спектров функций y(t) и e(t), и помеху считают более высокочастотной.
Синтез оптимального реализуемого фильтра является сложной задачей, для решения которой необходимо точное задание характеристик полезного сигнала и помехи. Поэтому на практике обычно задают передаточную функцию фильтра и ограничиваются параметрическим синтезом, применяя простые алгоритмы фильтрации.
Методы фильтрации осуществляют, как на программном уровне, так и на аппаратном. Например, в датчике BMP280 (BOSCH) имеется возможность подключить БИХ-фильтр на аппаратном уровне, изменяя по необходимости коэффициент фильтрации k, [1].
БИХ-фильтр
Фильтры с бесконечной импульсной характеристикой относятся к рекурсивным фильтрам и вычисляют выходной сигнал на основании значений предыдущих входных и выходных отсчётов. Теоретически, импульсная характеристика БИХ-фильтра никогда не достигает нуля, поэтому выход получается бесконечным по длительности.
В общем виде, алгоритм фильтрации одномерного скалярного цифрового фильтра запишем, как [2]:
, (1),
где T – скалярная функция одной переменной.
Функция T зависит от текущего входного сигнала x[n], и предыдущих: M отсчётов входного сигнала
 и N отсчётов выходного сигнала
и N отсчётов выходного сигнала 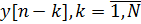
Выход БИХ-фильтра описывают разностным уравнением вида:
 (2),
(2),где x[n], y[n] – вход и выход фильтра, соответственно, {} – набор прямых коэффициентов, M – число прямых коэффициентов, {} – набор обратных коэффициентов, N – число обратных коэффициентов.
Применяя z-преобразование к обеим сторонам уравнения (2), получим:
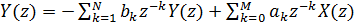 (3).
(3).Тогда передаточная функция фильтра будет выглядеть следующим образом:
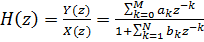 (4)
(4)Алгоритм фильтрации одномерного БИХ-фильтра
В общем виде алгоритм фильтрации одномерного скалярного стационарного рекурсивного фильтра выглядит так:
. (5)
Запишем теперь разностное уравнение для БИХ-фильтра в виде [1]:
 (6),
(6),где k – коэффициент фильтра;
или
(7),
где
 – обратный и прямой коэффициенты фильтра, соответственно.
– обратный и прямой коэффициенты фильтра, соответственно.Из (7) очевидно, что при k=1 выходной сигнал фильтра будет повторять входной, и при увеличении коэффициента фильтра k вес предыдущего фильтрованного сигнала стремится к 1, а вес измеренного значения стремится к 0.
Алгоритм (6) реализован на примере информационно-измерительного канала абсолютного атмосферного давления для датчика BMP280, на программном уровне в среде разработки Arduino Software (IDE), листинг 1. Электрическая схема подключений компонентов ИИК представлена на рис. 1. Общий вид прототипа ИИК абсолютного атмосферного давления представлен на рис. 2. В прототипе предусмотрена возможность изменять коэффициент фильтрации в диапазоне 1…50 с шагом 1, вращением ручки потенциометра. На экране знакового жидкокристаллического дисплея отображается измеренное значение давления (при k = 1) или фильтрованное значение (при k = 2…50), и значение коэффициента фильтрации k.
//ИИК абсолютного атмосферного давления (температуры)
//цель - исследование БИХ-фильтров
//https://github.com/orgua/iLib/blob/master/src/i2c.h
#include "i2c.h"
//https://github.com/orgua/iLib/blob/master/src/i2c_BMP280.h
#include "i2c_BMP280.h"
//https://github.com/arduino-libraries/LiquidCrystal
#include <LiquidCrystal.h>
//https://github.com/orgua/iLib/tree/master/examples/i2c_BMP280
BMP280 bmp280;
const int rs = 12, en = 11, d4 = 6, d5 = 5, d6 = 4, d7 = 3;
//const int rs = PB4, en = PB3, d4 = PD6, d5 = PD5, d6 = PD4, d7 = PD3;
LiquidCrystal lcd(rs, en, d4, d5, d6, d7);
float pascal_f = 100500;
float filter_K = 1;
const int analogInPin = A0; //аналоговый вход от потенциометра
int sensorValue = 0; //сигнал от потенциометра
int outputValue = 0;
void setup()
{
Serial.begin(9600);
//Serial.print("Probe BMP280: ");
if (bmp280.initialize()) {
//Serial.println("Sensor found");
;
}
else
{
Serial.println("Sensor missing");
while (1) {}
}
bmp280.setEnabled(0);
bmp280.triggerMeasurement();
bmp280.setFilterRatio(0);
lcd.begin(16, 2);
lcd.setCursor(0, 0);
lcd.print("measure");
lcd.setCursor(7, 1);
lcd.print("Pa");
lcd.setCursor(10, 0);
lcd.print("filter");
}
void loop()
{
float temperature;
float pascal, hpascal;
sensorValue = analogRead(analogInPin);
outputValue = map(sensorValue, 0, 1023, 1, 50);
filter_K = outputValue;
bmp280.awaitMeasurement();
bmp280.getTemperature(temperature);
temperature -= 1.7; //поправка
bmp280.getPressure(pascal);
pascal -= 50;//поправка
hpascal = pascal/100.;
bmp280.triggerMeasurement();
pascal_f = (pascal_f * (filter_K - 1) + pascal) / filter_K; //(6)
Serial.println(pascal_f,0);
if(pascal_f < 100000)
lcd.setCursor(6, 1);
lcd.print(" ");
lcd.setCursor(0, 1);
lcd.print(pascal_f,0);
if(filter_K < 10)
lcd.setCursor(13, 1);
lcd.print(" ");
lcd.setCursor(10, 1);
lcd.print(filter_K,1);
delay(300);
}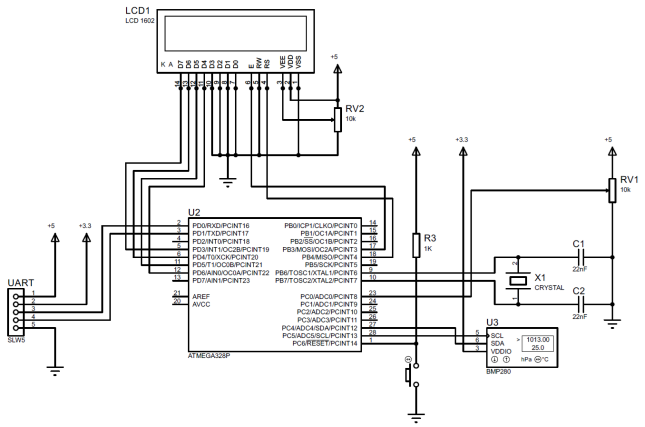
Рис. 1 – Электрическая схема подключений компонентов прототипа ИИК

Рис. 2 – Общий вид прототипа ИИК
Python-cкрипт для исследования БИХ-фильтров
На листинге 2 представлен Python-cкрипт для исследования БИХ-фильтров. Коэффициент фильтрации k прописываем в скрипте. Измеренные значения давления последовательно считываются с виртуального COM-порта и фильтруются. В графическое окно и на консоль выводятся измеренные и фильтрованные значения измеряемого параметра в реальном режиме времени. Результаты эксперимента записываются таблицей в файл, а в графическое окно выводятся временные графики измеренных и фильтрованных значений.
import numpy as np
import matplotlib.pyplot as plt
import serial
from drawnow import drawnow
import datetime, time
k = 6.0 #коэффициент фильтрации + 1
filter_K = 1 + k
#вывод выборки в графическое окно
def cur_graf():
plt.title("BMP280")
plt.ylim( 100450, 100510 )
plt.plot(nw, lw1, "r.-", label='измеренное')
plt.plot(nw, lw1f, "b.-", label='фильтрованное')
plt.legend(loc='best')
plt.ylabel(r'$давление, Па$')
plt.xlabel(r'$номер \ измерения$')
plt.grid(True)
#вывод всех списков в графическое окно
def all_graf():
plt.close()
fig=plt.figure()
ax = fig.add_subplot(111)
fig.subplots_adjust(top=0.85)
ax.set_title("датчик BMP280\n" +
str(count_v) + "-й эксперимент " +
"(" + now.strftime("%d-%m-%Y %H:%M") + ")")
ax.set_ylabel(r'$давление, Па$')
ax.set_xlabel(r'$номер \ измерения$' +
'; (период опроса датчика: {:.6f}, c)'.format(Ts))
ax.text(0.95, 0.03,
"Коэффициент фильтра: " + str(filter_K) + "\n",
verticalalignment='bottom', horizontalalignment='right',
transform=ax.transAxes,
color='black', fontsize=14)
plt.plot( n, l1, "r-", label='измеренное')
plt.plot( n, l1f, "b-", label='фильтрованное')
plt.legend(loc='best')
plt.grid(True)
plt.show()
#определяем количество измерений
# общее количество измерений
str_m = input("введите количество измерений: ")
m = eval(str_m)
# количество элементов выборки
mw = 16
#настроить параметры последовательного порта
ser = serial.Serial()
ser.baudrate = 9600
port_num = input("введите номер последовательного порта: ")
ser.port = 'COM' + port_num
ser
#открыть последовательный порт
try:
ser.open()
ser.is_open
print("соединились с: " + ser.portstr)
except serial.SerialException:
print("нет соединения с портом: " + ser.portstr)
raise SystemExit(1)
#определяем списки
l1 = [] # для значений давления
l1f = [] # для фильтрованных значений давления
t1 = [] # для значений моментов времени
lw1 = [] # для значений выборки давления
lw1f= [] # для фильтрованных значений выборки давления
n = [] # для значений моментов выборки
nw = [] # для значений выборки моментов времени
#подготовить файлы на диске для записи
filename = 'count.txt'
in_file = open(filename,"r")
count = in_file.read()
count_v = eval(count) + 1
in_file.close()
in_file = open(filename,"w")
count = str(count_v)
in_file.write(count)
in_file.close()
filename = count + '_' + filename
out_file = open(filename,"w")
#вывод информации для оператора на консоль
print("\nпараметры:\n")
print("n - номер измерения;")
print("P - давление, Па;")
print("\nизмеряемые значения величины давления\n")
print('{0}{1}\n'.format('n'.rjust(4),'P'.rjust(10)))
#считывание данных из последовательного порта
#накопление списков
#формирование текущей выборки
#вывод значений текущей выборки в графическое окно
i = 0
while i < m:
n.append(i)
nw.append(n[i])
if i >= mw:
nw.pop(0)
line1 = ser.readline().decode('utf-8')[:-2]
t1.append(time.time())
if line1:
l1.append(eval(line1))
lw1.append(l1[i])
if i :
l1f.append( (l1f[i-1]*(filter_K - 1) + l1[i])/filter_K ) #(6)
lw1f.append(l1f[i])
else :
l1f.append(l1[i])
lw1f.append(l1f[i])
if i >= mw:
lw1.pop(0)
lw1f.pop(0)
print('{0:4d} {1:10.2f} {2:10.2f}'.format(n[i],l1[i],l1f[i]) )
drawnow(cur_graf)
i += 1
#закрыть последовательный порт
ser.close()
ser.is_open
time_tm = t1[m - 1] - t1[0]
print("\nпродолжительность времени измерений: {0:.3f}, c".format(time_tm))
Ts = time_tm / (m - 1)
print("\nпериод опроса датчика: {0:.6f}, c".format(Ts))
#запись таблицы в файл
print("\nтаблица находится в файле {}\n".format(filename))
for i in np.arange(0,len(n),1):
count = str(n[i]) + "\t" + str(l1[i]) + "\n"
out_file.write(count)
#закрыть файл с таблицей
out_file.close()
out_file.closed
#получить дату и время
now = datetime.datetime.now()
#вывести график в графическое окно
all_graf()
end = input("\nнажмите Ctrl-C, чтобы выйти ")
Результаты эксперимента
введите количество измерений: 33
введите номер последовательного порта: 6
соединились с: COM6
параметры:
n - номер измерения;
P - давление, Па;
измеряемые значения величины давления
n P
0 100490.00 100490.00
1 100488.00 100489.71
2 100487.00 100489.33
3 100488.00 100489.14
4 100488.00 100488.97
…
30 100486.00 100488.14
31 100492.00 100488.70
32 100489.00 100488.74
продолжительность времени измерений: 16.028, c
период опроса датчика: 0.500875, c
таблица находится в файле 275_count.txt
нажмите Ctrl-C, чтобы выйти


Выводы
Приведенный алгоритм фильтрации очень прост в программной реализации и, практически, может быть использован в ИИК, подобных рассмотренному в этой статье.
В работе принимал участие Лосихин Д.А., с.в. каф. КИТиМ.
Источники информации
Комментарии (17)

BelerafonL
24.06.2018 22:42Да, чет сложновато будет, мы студентам объясняем фильтры так.
Выход фильтра равен самому себе, плюс небольшая поправка, пропорциональная разнице входа и выхода.
y = y + 0.1*(x-y);
Коэффициент перед скобкой подбирать, чем меньше, тем сильнее фильтрует. Готово.
vasimv
25.06.2018 01:35Когда нужно свести вместе, например, данные от гироскопа и компаса/акселерометра — похожий алгоритм применяют. yaw = (yaw + gyro_yaw) + K * compass_yaw. Гироскоп будет в приоритете (как более шустрый), но если от него и придет какая-то ошибка из-за шумов и/или низкой точности, то постепенно выровняется по более медленному компасу.

Arastas
25.06.2018 13:52Как будете объяснять фильтры более высоких порядков?

BelerafonL
25.06.2018 13:57«Если нужен фильтр более высокого порядка, поставьте две таких формулы друг за другом». Для начала так, а если кому что сложнее надо, то да, уже есть книжки с выводом через дискретную область и все такое. На практике студентам хватает первого порядка обычно (для наших задач электропривода).

Arastas
25.06.2018 14:07Чисто занудства ради: не каждый фильтр второго порядка может быть получен как соединение двух фильтров первого порядка.

BelerafonL
25.06.2018 14:11Конечно, никто не спорит, что есть много хороших и разных фильтров, сложных и простых. Но на практике, обычно, для фильтрации измерения температуры и многих других сигналов вот той простой формулы сверху более чем достаточно. Даже высокого порядка не нужно.

CrazyFizik
25.06.2018 14:56Чисто на практике для фильтрации сигналоа и 12-й порядок БИХ-фильтра далеко не предел, ещё и с особыми требованиями к соотношению нулей и полюсов и особы требованиями к особенностям ФЧХ и АЧХ, а получиться фильтра 11-го фильтра — и все будут плясать от счастья.
Для фильтрации данных температурного датчика нужен ФНЧ — и Вы выше приводите реккурентную формулу ФНЧ 1-го порядка с очень фиговым хвостатым АЧХ — это тоже самое что и RC-цепочку на вход датчика повесить — прашивается, причём тут цифровая обработка сигналов?
BelerafonL
25.06.2018 15:09Было бы интересно почитать общеобразовательную статью про реальные задачи, где нужен фильтр 12го порядка и какие нюасны его синтеза возникают на пути. В моей области большинство проблем решаются ФНЧ 1-го порядка, и чем формулы проще и быстрее считаются, тем лучше. RC-цепочка же проигрывает программному эквиваленту гибкостью настройки и возможностью введения/изменения фильтрации сигнала удаленной перепрошивкой.

CrazyFizik
25.06.2018 16:54+1Любая задача где нужен крутой спад АЧХ, полосовая фильтрации, малые неравномерности (риппли) — радиолокация, радиосвязь — в общем везде, где надо получить АЧХ в виде идеального прямоугольник с очень высоким подавление и ещё подумать о ГВЗ, ФЧХ и т. П. Или АЧХ очень специфический формы. Например, в той же базовой станции сотовой связи мощность TX будет 23dBm, а чувствительность RX должна быть не хуже чем -98.8 dBm при SNR порядка 5dB, а полосы у них находятся совсем рядом — это вот требования по уже устаревшему 3G стандарту (на память). В итоге у нас гигантский TX и мизерный RX, и их надо как-то разделять, причём в широкой полосе, причём ещё TX своими интермодуляциями лезет в канал приёмника.
В цифре естественно будут до последнего пытаться использовать FIR, т.к. он хотя бы устойчивый, до тех пор пока умножалки на кристалле не закончаться. Для FIR фильтров порядки исчисляется десятками, сотнями и даже тысячами, IIR фильтр будет получаться поменьше, но тоже явно выше 2-го порядка.
А в аналоговой части, которая стоит дорого и занимает много места — там только IIR, ну вот например в роли дуплексеров базовых станций, про которые я упомянул, обычно используются, т.н. Cavity Filters — эт такие коробочки с полостями, внутри которых ещё и коаксиальный проводник — загуглите, у меня на первой же картинки вываливается фильтр 8-го порядка с 2-мя нулями — а это ещё фиговый фильтр и после него все равно придётся чистить и его все равно надо как-то рассчитывать.
Плюс есть отдельная область — адаптивной фильтрации, где в реальном времени адаптируется коэффициенты фильтра и их много — десятки и сотни (FIR), например, для той же echo cancelation — там задержки могут быть ого-го какими большими, а это наверное самая простая и линейная задача. Кстати нынче модная тема — нейронные сети, как раз и есть ответвление от адаптивной фильтрации — много там коэффициентов? Да до фига — линейный однослойный персептрон с n-входами — это FIR фильтр порядка n (пруфы у Хайкина), Black propagation — ну примерно тоже самое, что и LMS в адаптивнрй фильтрации, добавили обратную связь — и получили уже IIR.
Или High Order Kalman Filters (ой этих каламновских фильтров вообще до фига наплодили) — тоже можно за бих считать — они все большие и сложные, а применяются в той же навигации, ЭКГ и т.д.
Ну а Вы приводите достаточно простой пример и ещё и частный случай: там по-моему формула y[i] = a * x[i] + (1-a) * y[i-1] и там путем математических манипуляций получаем Вашу формулу: y[i] = y[i-1] + a * (x[i] — y[i-1]) — совсем частный случай, так ещё и в нестандартный форме. При этом это даже и не совсем полноценный фильтр (с утилитарной точки зрения конечно) — просто штука которая сглаживает отсчёты и добавляет немного инертности системе (что не всегда хорошо) а вот отфильтровать сигнал в полосе эдак мегагерц в 100 идеальным прямоугольник такой формулой уже не получиться. Я если честно пока Вы про температуру не написали, все никак не мог вспомнить — что это такое и куда это можно впихнуть.
Arastas
25.06.2018 18:27Я в целом согласен, но почти полностью уверен, что адаптивный FIR c LMS настройкой не эквивалентен IIR, так как является нелинейной системой. Или вы что-то другое имели ввиду?

CrazyFizik
25.06.2018 18:59Другое. Я пытался от фильтров перейти к более попсовому примеру, ведь линейный однослойный персептрон обучаемый бэк-ппоопагейшеном — это примерно тоже самое что и адаптивный FIR фильтр обучаемый по LMS — по-моему к обоим руку приложил Уидроу в одно и тоже время(он ещё кстати живой и ведёт свой канал на Ютубе!).
Потом снова берём эту нейросеть, начинаем усложнять её топологии, добавляем обратную связь — получаем реккурентную ИНС которая… ну по факту получается терь IIR фильтр. Ну и возвращаясь к изнальному вопросу — сколько на практике в фильтрах может быть коэффициентов — ну вот у нас сейчас есть те же нейросети которые у всех на слуху, все с их помощью пытаются распознавать котиков, строить регрессионные модели курса биткоина и которые из себя представляют адаптивные IIR и FIR фильтры на стероидах — вот сколько там коэффициентов? Да до фига и нужно ещё больше.
Ну т.е. найти задачу, где нужно фильтры офигенно большого порядка, наткнуться на динамическую систему супер-высокого порядка — это вообще не проблема — таких задач полно, хоть в радиосвязи, хоть в распознавания котиков, хоть в управление роботами (шагающие двуногие фиговины тоже далеко не самые простые системы) — куча их, и все они прыгают вокруг одной математики (только разные задачи и приёмы, но суть также). А вот обратная ситуация — как уменьшить количество умножалое — ха! Это вот уже серьезная проблема.
Есть пара хороших задач, например, сглаживание медленно-меняющихся данных или компенсация постоянной составляющей сигнала, где мы можем обойтись простыми фильтрами 1-го порядка, вот только практических задач где надо использовать фильтры с двух-трехзначным порядком ещё больше!
Поэтому мне пример в котором всю фильтрацию можно раскрыть показав одну формулу — модель RC цепочки — мне не очень понравился, т.к. Надо все объяснять на фундаментальных вещах: свертки там всякие, Фурье, Лапласс и т.д. — простые формулы, простые понятия, которые можно распространить на что угодно. А куда можно распространять один специфический сглаживающий фильтр?

Arastas
25.06.2018 18:24+1Вы приводами занимаетесь? Пожалуйста. Для повышения точности слежения надо было повышать "агрессивность" регулятора (иначе говоря, повышать полосу пропускания, улучшать добротность, повышать быстродействие, много синонимов). Но у механической нагрузки был резонанс, который плавал, в зависимости от внешних параметров, в диапазоне шириной 20Гц. Чтобы этот резонанс не возбуждал систему, весь диапазон вырезался band-stop фильтром 14-го порядка.

CrazyFizik
25.06.2018 19:03Ну кстати да. Хороший пример, причём полоса то узкая — 20Гц всего, а уже надо воротить фильтр уравнение которого уже лень в тетрадку выписывать — слишком длинное

CrazyFizik
25.06.2018 14:33Ой хз. Фильтры студентам объясняются через свертку, Z-преобразование и преобразование Лапласса, да всякие импульсный характеристики и передаточные функции — чай не маленькие уже, а в фильтрах нас интересует только передаточная харакиеристика, а свертку и школьник поймёт — щадерживай умножаю да складывай.
Выход фильтра равен самому себе, плюс небольшая поправка, пропорциональная разнице входа и выхода.
y = y + 0.1*(x-y);
Если честно, то нифига не понятно: где другие X, куда они потерялисись? Какой из двух Y-ов, на сколько задержан? Более того:
1) Для КИХ фильтра это вообще абсолютно неверно — он просто домнажает и складывает все свои задержанные отсчеты
2) Да и для БИХ фильтра вообще-то тоже, хоть он и рекурсивный, но что в какнонической форме, что не в какнонической формах как минимум будет вычитаться сумма задержных выходных отсчетов, помноженных каждый на свой коэффициент, а не просто вход-минус-выход — это уже какой-то странный фильтр получается…
3) неканоничный. Как буд-то бы П-контроллер набухался с фильтром (они иногда встречаются) и решил прикинуться то-ли фильтром первого порядка, то ли второго — он ещё сам не определился :)
В общем какой-то он неканоничный. На П-регулятор который минимизирует невязку — похож, а на фильтр (в прикладной смысле) — не особо, т.к. на беглый взгляд он ничего не фильтрует, зато наверное будет пытаться удерживать систему вокруг SP

FGV
25.06.2018 14:46Коэффициент перед скобкой подбирать, чем меньше, тем сильнее фильтрует. Готово.
Как то совсем не по инженерному. Есть же аналоговый собрат вида 1/(T*p+1), связь с приведенным в статье цифровым:
T=-ПериодВыборкиСигнала/ln(1-k).

dee3mon
25.06.2018 03:10+1Если кто-то решит дальше в цос, то сначала обратите внимание, как в источнике, из которого берете формулы, обозначаются коэффициенты прямой и рекурсивной ветвей фильтра. В этой части в разных книгах полный разброд. В старых книгах, типа Рабинера-Гоулда, прямая ветвь обозначается как Ak, а обратная как Bk. В более современнях (Сергиенке и матлабе например) наоборот, прямая идет как Bk, а рекурсивная как Ak. Также рекурсивная сумма может идти как 1 плюс сумма или как 1 минус сумма в знаменателе.
Если это не проследить, то применение влоб взятых формул может привести к неожиданным результатам.


aamonster
Зачем так сложно и наукообразно про такую простую вещь?