
Системы отсчёта для определения орбиты
Для нахождения траекторий относительных движений в классической механике используется предположение об абсолютности времени во всех системах отсчета (как инерциальных, так и неинерциальных).
Используя данное предположение, рассмотрим движение одной и той же точки в двух различных системах отсчета К и К', из которых вторая движется относительно первой с произвольной скоростью
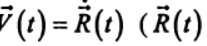 — радиус-вектор, описывающий положение точки начала системы координат К' относительно системы отсчета К).
— радиус-вектор, описывающий положение точки начала системы координат К' относительно системы отсчета К). Будем описывать движение точки в системе К' радиус-вектором
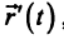 , направленным из начала координат системы К' в текущее положение точки. Тогда движение рассматриваемой точки относительно системы отсчета К описывается радиус-вектором
, направленным из начала координат системы К' в текущее положение точки. Тогда движение рассматриваемой точки относительно системы отсчета К описывается радиус-вектором 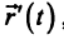 :
: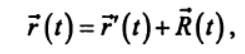 (1)
(1)а относительная скорость
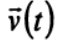
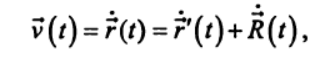 (2)
(2)где
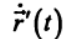 — скорость точки относительно системы К';
— скорость точки относительно системы К'; 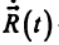 -скорость движения системы отсчета К' относительно системы отсчета К.
-скорость движения системы отсчета К' относительно системы отсчета К.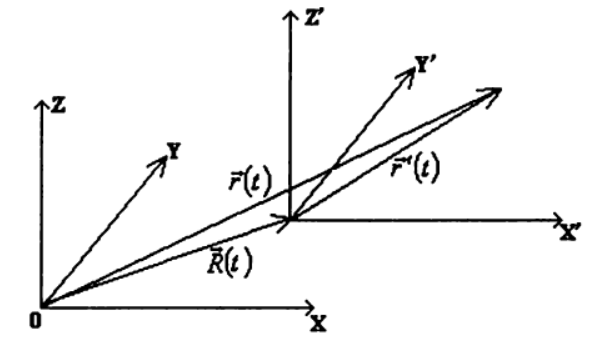
Таким образом, для нахождения закона движения точки в произвольной системе отсчета К необходимо:
1) задать закон движения точки относительно системы отсчета К' (функцию
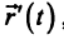 ;
;2) задать закон движения системы отсчета К' относительно системы отсчета К (функцию
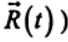 ;
;3) определить закон движения точки относительно системы отсчета К в соответствии с (1).
Построение орбиты Луны в гелиоцентрической системе отсчета
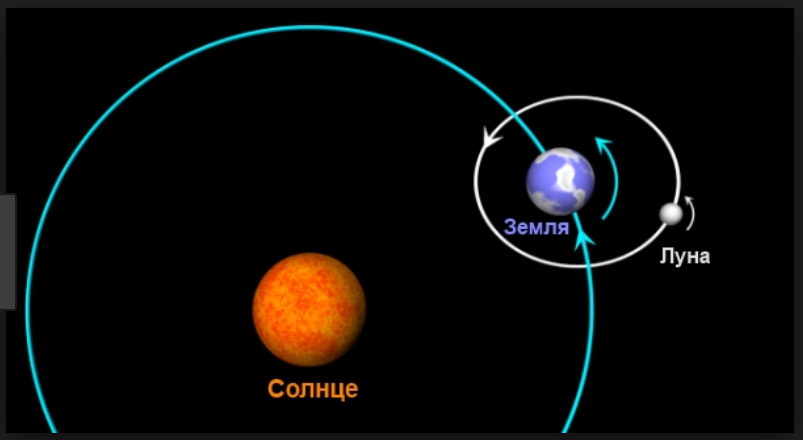
В гелиоцентрической системе отсчета (система К) Земля движется по окружности радиуса
R1 = 1.496*10**8 км (период обращения Т1= 3.156*10**7 с.). Луна, в свою очередь, движется вокруг Земли (система К') по окружности радиуса R2 = 3.844*10**5 км. (период обращения Т2= 2.36*10**6 с. Как известно [1,2], при движении материальной точки по окружности радиуса R с постоянной угловой скоростью
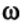 координаты радиус-вектора, проведенного из начала координат к текущему положению точки, меняются по закону:
координаты радиус-вектора, проведенного из начала координат к текущему положению точки, меняются по закону: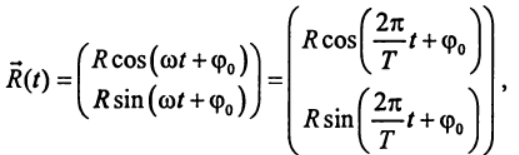 (3)
(3)где
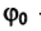 — начальная фаза, характеризующая положение частицы в момент времени t= 0, которую в дальнейшем мы будем полагать равной нулю. Заменяя в (3) R на R1 и R2 и подставляя в (1), получаем зависимость радиус-вектора Луны в гелиоцентрической системе координат от времени:
— начальная фаза, характеризующая положение частицы в момент времени t= 0, которую в дальнейшем мы будем полагать равной нулю. Заменяя в (3) R на R1 и R2 и подставляя в (1), получаем зависимость радиус-вектора Луны в гелиоцентрической системе координат от времени: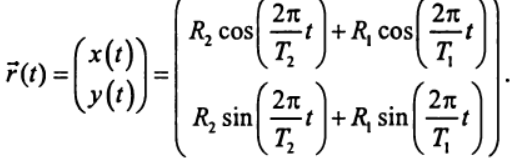 (4)
(4)Выражение (4) задает орбиту Луны
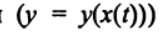 в параметрической форме, где параметром является время. Для построения искомой орбиты средствами Python, зададим радиусы орбит и периоды вращения Земли и Луны:
в параметрической форме, где параметром является время. Для построения искомой орбиты средствами Python, зададим радиусы орбит и периоды вращения Земли и Луны: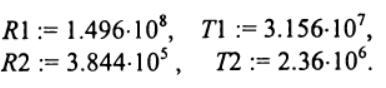
С учётом (4) определим функции зависимости координат от времени:
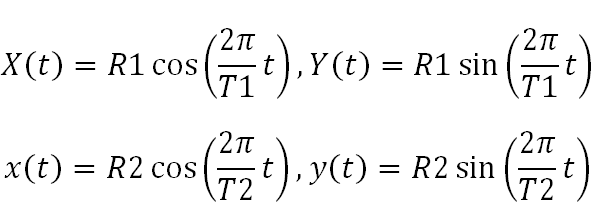 (5)
(5)Используя (5), получим пару координат для орбиты Луны:
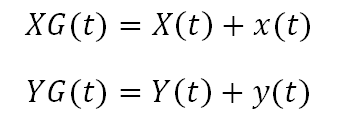 (6)
(6)Зададим число точек, в которых вычисляются координаты N=1000 и дискретное время на интервале периода вращения Земли dt=T1/N. Напишем программу и построим график для положительной области изменения координат:
from numpy import*
from matplotlib.pyplot import*
R1=1.496*10**8
T1=3.156*10**7
R2=3.844*10**5
T2=2.36*10**6
N=1000.0
def X(t):
return R1*cos(2*pi*t/T1)
def Y(t):
return R1*sin(2*pi*t/T1)
def x(t):
return R2*cos(2*pi*t/T2)
def y(t):
return R2*sin(2*pi*t/T2)
k=100
t=[T1*i/N for i in arange(0,k,1)]
X=array([X(w) for w in t])
Y=array([Y(w) for w in t])
x=array([x(w) for w in t])
y=array([y(w) for w in t])
XG=X+x
YG=Y+y
figure()
title("Траектория орбит Земли и Луны.\n Для положительных значений координат")
xlabel('X(t),XG(t)')
ylabel('Y(t),YG(t)')
axis([1.2*10**8,1.5*10**8,0,1*10**8])
plot(X,Y,label='Орбита Земли')
plot(XG,YG,label='Орбита Луны')
legend(loc='best')
grid(True)
show()Получим:
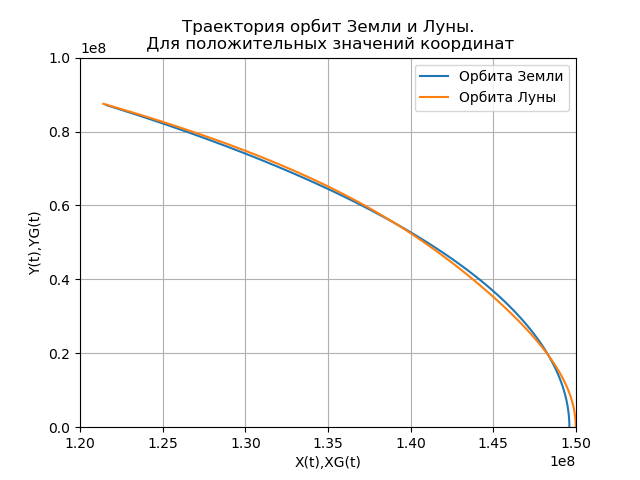
Рис.1
Созданный график позволяет расширить задачу и посмотреть какой будет орбита луны, если радиус орбиты Луны будет равен R2=3.844*10e7. Внесём соответствующие изменения в программу:
from numpy import*
from matplotlib.pyplot import*
R1=1.496*10**8
T1=3.156*10**7
R2=3.844*10**7
T2=2.36*10**6
N=1000.0
def X(t):
return R1*cos(2*pi*t/T1)
def Y(t):
return R1*sin(2*pi*t/T1)
def x(t):
return R2*cos(2*pi*t/T2)
def y(t):
return R2*sin(2*pi*t/T2)
t=[T1*i/N for i in arange(0,N,1)]
X=array([X(w) for w in t])
Y=array([Y(w) for w in t])
x=array([x(w) for w in t])
y=array([y(w) for w in t])
XG=X+x
YG=Y+y
figure()
title("Гелиоцентрическая орбита Земли и Луны")
xlabel('X(t),XG(t)')
ylabel('Y(t),YG(t)')
axis([-2.0*10**8,2.0*10**8,-2.0*10**8,2.0*10**8])
plot(X,Y,label='Орбита Земли')
plot(XG,YG,label='Орбита Луны')
legend(loc='best')
grid(True)
show()Получим:
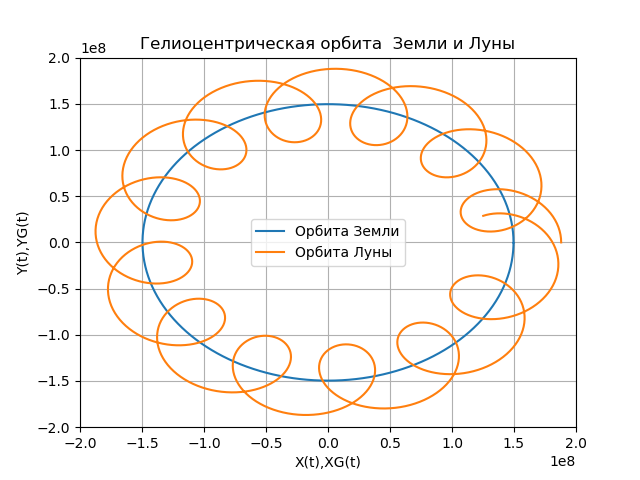
Рис.2
Сравнивая орбиты Луны, представленные на рис. 1 и 2, обнаруживаем их существенные отличия. Для объяснения причины этих отличий необходимо сравнить линейные скорости движения Луны в первом и во втором случае и линейную скорость движения Земли.
Так как направление линейной скорости движения Земли относительно Солнца, как и направление линейной скорости движения Луны относительно Земли, меняется во времени, а скорость остается постоянной по величине.
В качестве количественной характеристики соотношения линейных скоростей движения Луны и Земли в гелиоцентрической системе координат следует выбрать разность между модулем линейной скорости движения Земли и проекцией линейной скорости Луны на направление вектора линейной скорости Земли:
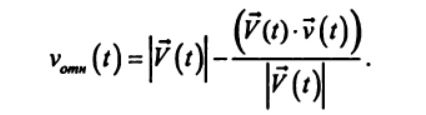 (7)
(7)Определим функции, описывающие законы изменения составляющих скорости Земли и Луны:
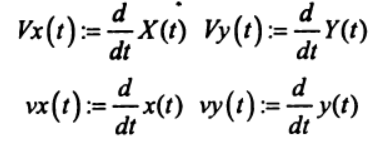 (8)
(8)Чтобы определить результирующую скорость с учётом проекции, воспользуемся соотношением:
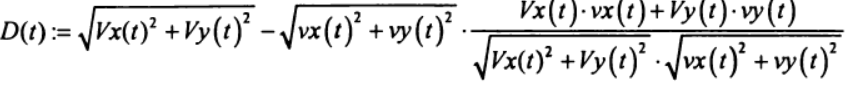 (9)
(9)Напишем программу с учётом(5), (8), (9) и радиуса орбиты Луны R2=3.844*10**5 км.:
from numpy import*
from matplotlib.pyplot import*
R1=1.496*10**8
T1=3.156*10**7
R2=3.844*10**5
T2=2.36*10**6
N=1000.0
k1=2*pi/T1
k2=2*pi/T2
def Vx(t):
return -k1*R1*sin(k1*t)
def Vy(t):
return k1*R1*cos(k1*t)
def vx(t):
return -k2*R2*sin(k2*t)
def vy(t):
return k2*R2*cos(k2*t)
def D(t):
return sqrt(Vx(t)**2+Vy(t)**2)-sqrt(vx(t)**2+vy(t)**2)*(Vx(t)*vx(t)+Vy(t)*vy(t))/((sqrt(Vx(t)**2+Vy(t)**2))*(sqrt(vx(t)**2+vy(t)**2)))
x=[T1*i/N for i in arange(0,N,1)]
y=[D(t) for t in x]
title("Луна движется в одном направлении с Землёй \n Радиус орбиты Луны R2=3.844*10**5 км.")
xlabel('t')
ylabel('D(t)')
plot(x,y)
show()Получим:
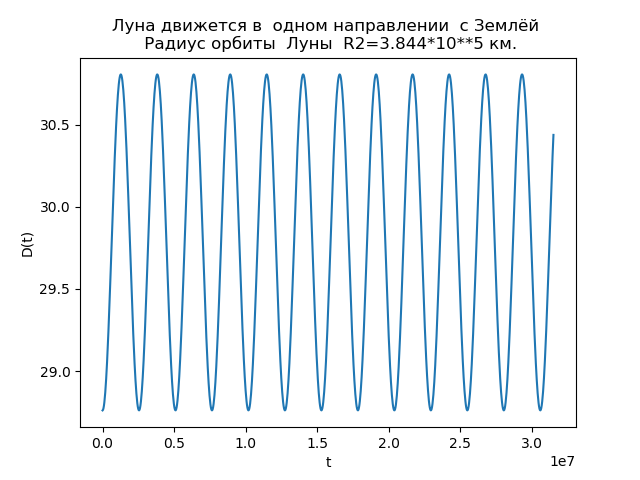
Рис.3.
Напишем программу с учётом (5), (8), (9) и радиуса орбиты Луны R2=3.844*10**7 км:
from matplotlib.pyplot import*
R1=1.496*10**8
T1=3.156*10**7
R2=3.844*10**7
T2=2.36*10**6
N=1000.0
k1=2*pi/T1
k2=2*pi/T2
def Vx(t):
return -k1*R1*sin(k1*t)
def Vy(t):
return k1*R1*cos(k1*t)
def vx(t):
return -k2*R2*sin(k2*t)
def vy(t):
return k2*R2*cos(k2*t)
def D(t):
return sqrt(Vx(t)**2+Vy(t)**2)-sqrt(vx(t)**2+vy(t)**2)*(Vx(t)*vx(t)+Vy(t)*vy(t))/((sqrt(Vx(t)**2+Vy(t)**2))*(sqrt(vx(t)**2+vy(t)**2)))
x=[T1*i/N for i in arange(0,N,1)]
y=[D(t) for t in x]
title(" Периодически Луна движется в противоположном к Земле \n направлению. Радиус орбиты Луны R2=3.844*10**7 км.")
xlabel('t')
ylabel('D(t)')
plot(x,y)
show()Получим:
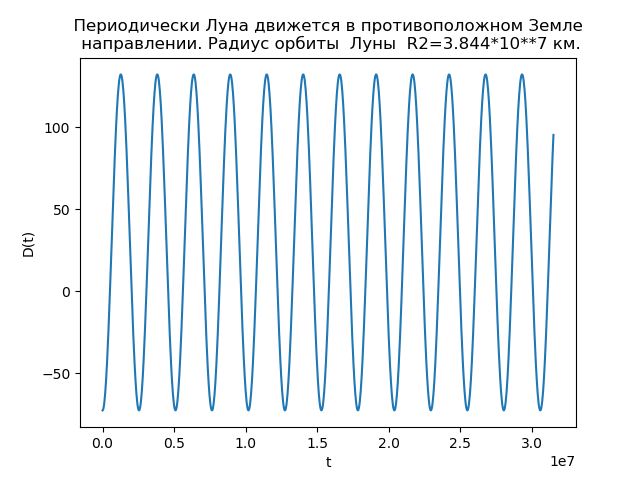
Рис.4.
Анализ зависимостей позволяет объяснить причину отличий орбит. Функция D(t) при R2 =3,844*10**5 км всегда положительна, т. е. Луна всегда движется в направлении движения Земли и петли не образуются. При R2 = = 3,844*10**7 км величина D(t) принимает отрицательные значения, т. е. существуют моменты времени, в которые Луна движется в направлении, противоположном направлению движения Земли, а потому орбита имеет петли.
Построение орбиты Марса в системе отсчета, связанной с Землей
.
В гелиоцентрической системе отсчета (система К) Земля движется по окружности радиуса R1= 1.496*10**8 км, период обращения Т1= 365.24 сут, Марс двигается по эллипсу, большая полуось которого ам = 2.28*10**8 км, период обращения Марса Тм = 689.98 сут., эксцентриситет орбиты е = 0.093 [3]. Движение Земли описывается радиус-вектором R(t), задаваемым выражением (3). В связи с тем, что орбита Марса является эллипсом, зависимости x=x(t), y=y(t) от времени задаются параметрически [4]:
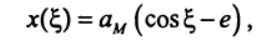 (10)
(10)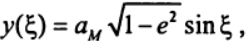 (11)
(11)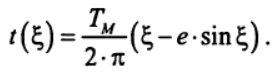 (12)
(12)Полному обороту по эллипсу соответствует изменение параметра
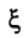 от 0 до
от 0 до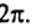 . Для построения орбиты Марса необходимо вычислить в одни и те же моменты времени координаты радиус-векторов, описывающих положение Земли и Марса в гелиоцентрической системе отсчета, затем в соответствии с соотношением
. Для построения орбиты Марса необходимо вычислить в одни и те же моменты времени координаты радиус-векторов, описывающих положение Земли и Марса в гелиоцентрической системе отсчета, затем в соответствии с соотношением 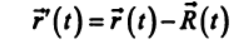 вычислить координаты Марса в системе отсчета, связанной с Землей.
вычислить координаты Марса в системе отсчета, связанной с Землей. Для построения орбиты Марса в системе отсчёта связанной с Землёй воспользуемся ранее приведенными параметрами орбит Земли и Марса, соотношениями (10)-(12), а также соотношениями для координат Земли:
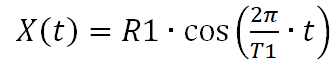 (13)
(13)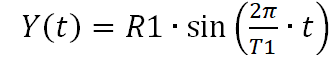 (14)
(14)Следует учесть, что число периодов обращения Марса вокруг Солнца равно K=9, тогда количество точек, в которых следует произвести расчёт и расстояние между ними, будут определяться из соотношений:
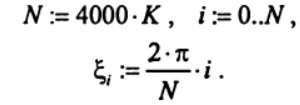 (15)
(15)from numpy import*
from matplotlib.pyplot import*
R1=1.496*10e8
T1=365.24
am=2.28*10e8
Tm=689.98
ee=0.093
N=36000
def x(g):
return am*(cos(g)-ee)
def y(g):
return am*sqrt(1-ee**2)*sin(g)
def t(g):
return Tm*(g-ee*sin(g))/2*pi
def X(g):
return R1*cos(2*pi*t(g)/T1)
def Y(g):
return R1*sin(2*pi*t(g)/T1)
y=array([y(2*pi*i/N) for i in arange(0,N,1)])
x=array([x(2*pi*i/N) for i in arange(0,N,1)])
X=array([X(2*pi*i/N) for i in arange(0,N,1)])
Y=array([Y(2*pi*i/N) for i in arange(0,N,1)])
t=array([t(2*pi*i/N) for i in arange(0,N,1)])
figure()
title("Гелиоцентрические орбиты Земли и Марса")
xlabel('x(g),X(g)')
ylabel('y(g),Y(g)')
plot(x,y,label='ОрбитаМарса')
plot(X,Y,label='ОрбитаЗемли')
legend(loc='best')
figure()
title("Положение Марса в системе отсчёта связанной с Землёй")
xlabel('x1/10e8')
ylabel('y1(g/10e8')
x1=(x-X)
y1=(y-Y)
plot(x1/10e8,y1/10e8)
figure()
title("Зависимость расстояния между Землёй и Марсом \n от времени в годах")
xlabel('t/365.24')
ylabel('sqrt(x1**2+y1**2)/10e8')
y2=sqrt(x1**2+y1**2)/10e8
x2=t/365.24
plot(x2,y2)
show()Получим:
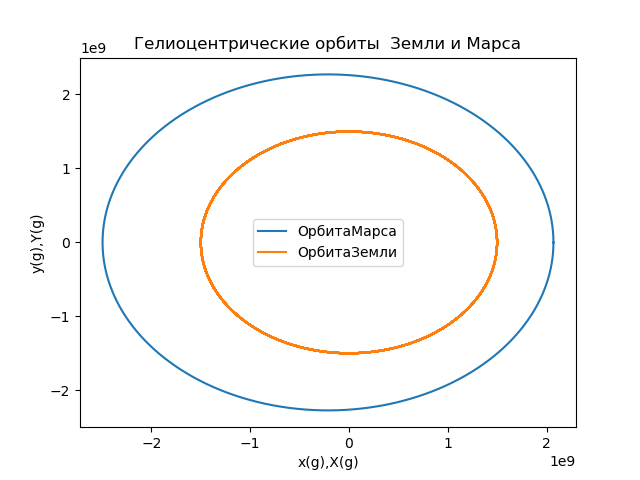
Рис.5
Вычислим координаты радиус-вектора, описывающего положение Марса в системе отсчета связанной с Землей, и построим орбиты (Рис.6), используя соотношение:
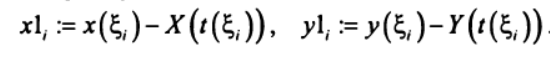 (16)
(16)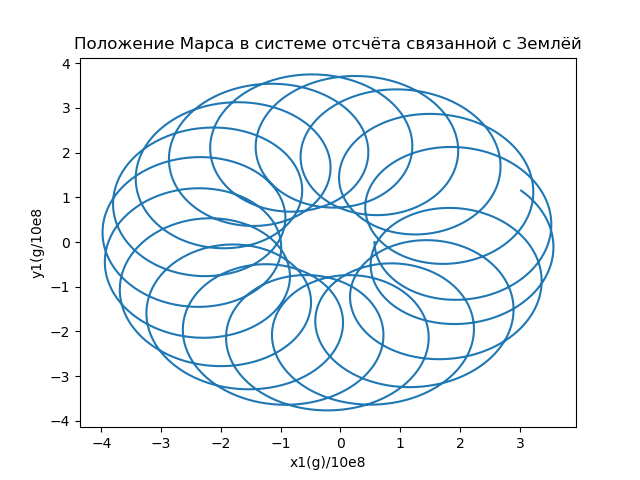
Рис.6
Еще одной важной характеристикой движения Марса (в первую очередь для межпланетных космических полетов) является расстояние между Землей и Марсом s(t), которое определяется модулем радиус-вектора, описывающего положение Марса в системе отсчета, связанной с Землей. Зависимость расстояния между Землей и Марсом от времени, измеряемого в земных годах, представлена на рис.7.
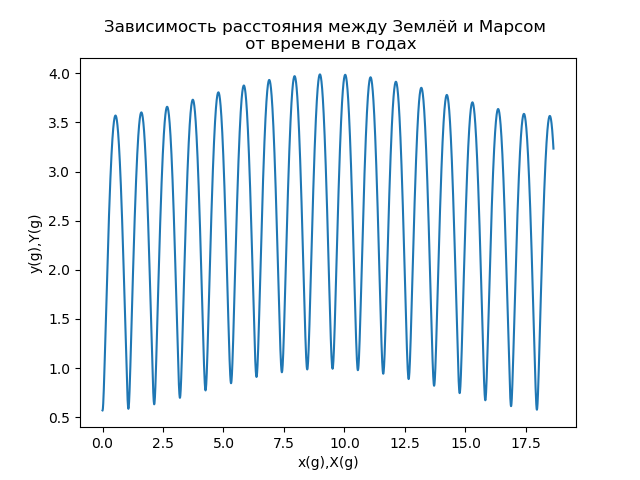
Рис.7
Анализ зависимости, представленной на рис.7, показывает, что расстояние между Землей и Марсом является сложной периодической функцией времени. Если воспользоваться терминологией теории сигналов [5], то о зависимости s(t) можно сказать, что она представляет собой амплитудно-модулированный сигнал, который принято представлять в виде произведения двух функций высокочастотной (несущей) и низкочастотной функции, задающей амплитудную модуляцию (огибающей):
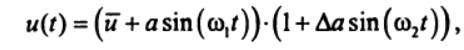 (17)
(17)где
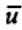 — постоянная составляющая функции u(t); а — амплитуда сигнала; — частота несущей;
— постоянная составляющая функции u(t); а — амплитуда сигнала; — частота несущей; 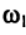
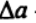 — амплитуда функции, задающая глубину амплитудной модуляции;
— амплитуда функции, задающая глубину амплитудной модуляции; 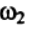 — частота модулирующей функции.
— частота модулирующей функции.Из рис.7 видно, что период несущей составляет примерно 2 года, период модулирующей функции примерно 17 лет]6].
Построение гелиоцентрической орбиты кометы Галлея

В последний раз комета Галлея проходила через свой перигелий (ближайшая к Солнцу точка орбиты) 9 февраля 1986 года. (Само Солнце считается расположенным в начале координат.)
Координаты и компоненты скорости кометы Галлея в тот момент были равны P0 = (0.325514, 0.459460, 0.166229) и v0 = (–9.096111, –6.916686, –1.305721) соответственно, причем расстояние здесь выражено в астрономических единицах длины – а.е.д., или просто а.е. (астрономическая единица, т. е. длина большой главной полуоси земной орбиты), а время – в годах. В этих единицах измерения трехмерные уравнения движения кометы имеют вид:
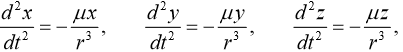 (18)
(18)где:
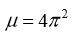 ,
,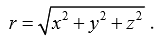
from numpy import*
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
def f(y, t):
y1, y2, y3, y4,y5,y6 = y
return [y2, -(4*pi*pi*y1)/(y1**2+y3**2 +y5**2)**(3/2),y4,-(4*pi*pi*y3)/(y1**2+y3**2 +y5**2)**(3/2),y6,-(4*pi*pi*y5)/(y1**2+y3**2 +y5**2)**(3/2)]
t = linspace(0,300,10001)
y0 = [0.325514,-9.096111, -0.459460,-6.916686,0.166229,-1.305721]
[y1,y2, y3, y4,y5,y6]=odeint(f, y0, t, full_output=False).T
fig, ax = plt.subplots()
plt.title("Орбита кометы Галлея(расстояние в а.е., время в годах) \n Солнце в центре координат")
plt.xlabel('x(t)')
plt.ylabel('y(t)')
fig.set_facecolor('white')
ax.plot(y1,y3,linewidth=1)
circle = Circle((0, 0), 0.2, facecolor='orange')
ax.add_patch(circle)
plt.axis([1,-21,-1,29])
plt.grid(True)
fig, ax = plt.subplots()
plt.title("Орбита кометы Галлея \n Солнце в центре координат")
plt.xlabel('x(t)')
plt.ylabel('z(t)')
fig.set_facecolor('white')
ax.plot(y1,y5,linewidth=1)
circle = Circle((0, 0), 0.1, facecolor='orange')
ax.add_patch(circle)
plt.axis([1,-21,1,-11])
plt.grid(True)
fig, ax = plt.subplots()
plt.title("Орбита кометы Галлея \n Солнце в центре координат")
plt.xlabel('y(t)')
plt.ylabel('z(t)')
fig.set_facecolor('white')
ax.plot(y3,y5,linewidth=1)
circle = Circle((0, 0), 0.2, facecolor='orange')
ax.add_patch(circle)
plt.axis([-1,29,1,-11])
plt.grid(True)
fig, ax = plt.subplots()
plt.title("Проекция скорости движения кометы Галлея \n на плоскости ZOX и ZOY ")
ax.plot(t,y1,linewidth=1)
ax.plot(t,y3,linewidth=1)
plt.show()Получим:
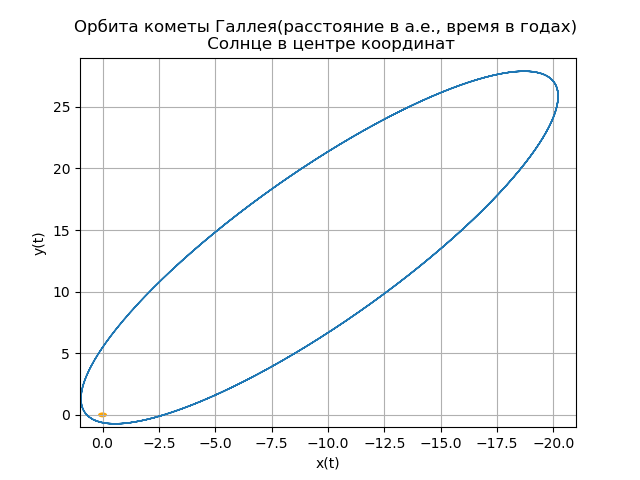

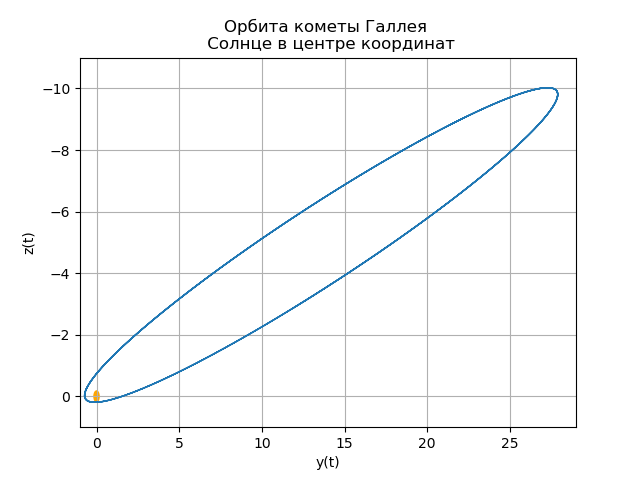
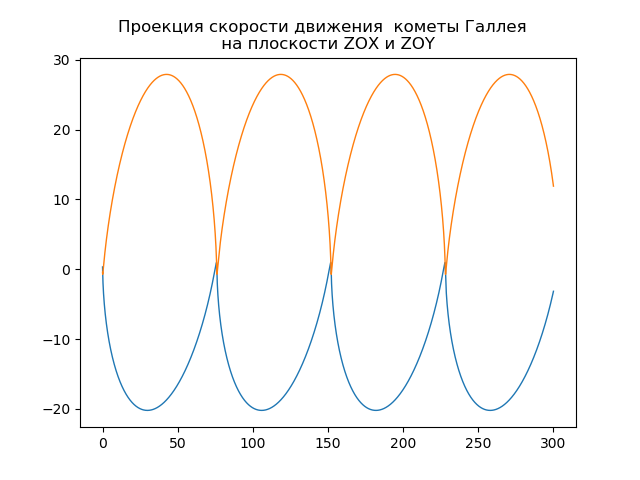
Ваша собственная комета
Попробуйте провести эксперимент. В ночь вы установите свой телескоп на вершине, недалеко расположенной от вашего дома возвышенности. Ночь должна быть ясной, безоблачной, звездной и, если вам улыбнулась фортуна: в 0 часов 30 минут ночи вы заметите новую комету.
После повторных наблюдений в следующие ночи вам удастся вычислить ее координаты в ту первую ночь. Координаты в гелиоцентрической системе координат: P0= (x0, y0, z0) и и вектор скорости v0 = (vx0, vy0, vz0).
Используя эти данные, определите:
- расстояние кометы от Солнца в перигелии (самая близкая к Солнцу точка орбиты) и в афелии (самая дальняя от Солнца точка орбиты);
- скорости кометы при прохождении через перигелий и через афелий;
- период обращения кометы вокруг Солнца;
- следующие две даты прохождения кометы через перигелий.
Если измерять расстояние в астрономических единицах, а время — в годах, то уравнение движения кометы примут вид (18). Для вашей собственной кометы выберите произвольные начальные координаты и скорости того же порядка, что и у кометы Галлея.
В случае необходимости, повторно осуществляйте произвольный выбор начального положения и вектора скорости до тех пор, пока не получите правдоподобную эксцентрическую орбиту, выходящую за пределы орбиты Земли (как у большинства настоящих комет).
Ссылки:
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. 3-е изд. Т. 1.-2. М.: Мир, 1977.
- Матвеев А. Н. Механики и теория относительности. М.: Высш. шк., 1986.
- Физическая энциклопедия. Т. 3. М.: Большая российская энциклопедия, 1992.
- Ландау Л. Д., Лифшиц Е. М. Курс теоретической физики. Механика. М.: Фю-матгиз, 1958.
- Баскаков С. И. Радиотехнические цепи и сигналы. М.: Высш. шк., 1988.
- Поршнев C.В. Компьютерное моделирование физических процессов с использованием пакета mathcad.
Комментарии (57)

a-tk
12.08.2018 13:19Казалось бы, при чём здесь вообще Python?

maisvendoo
12.08.2018 13:32Просто это единственный ЯП, который автор смог освоить, и теперь, на протяжении нескольких десятков публикаций, усиленно этим хвалится.
P.S.: На хабре уже давным-давно сделали возможность вводить формулы. Вот, спрашивается, для кого? Всё равно продолжают лепить картинками

pchelintsev_an
12.08.2018 15:32Юрий, не пробовали исследовать устойчивость построенных орбит? Хотя бы численно — взять небольшую ошибку в начальных условиях и посмотреть, как далеко разбегутся траектории, и найти при этом критический момент времени, когда расстояние между ними по Евклиду превысит допустимой величины. В этом же контексте интересно изучить, как влияет на это дело шаг интегрирования. Например, для гелиоцентрической орбиты кометы Галлея.

Scorobey Автор
12.08.2018 16:22Спасибо за комментарий!
Обязательно попробую, но у других авторов такие орбиты выглядят вот так
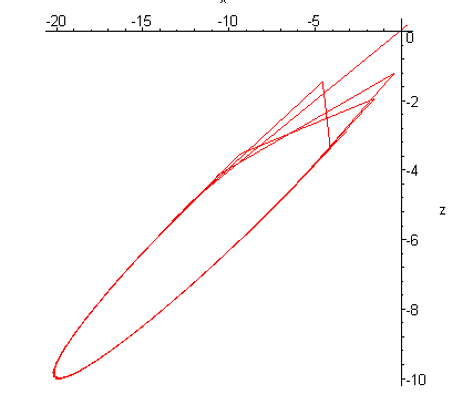

pchelintsev_an
12.08.2018 16:42А «пила» на рисунке — это шаг интегрирования большой?

Scorobey Автор
12.08.2018 17:12Не только, Python позволяет более точно отражать характер соотношений при численном интегрировании, поэтому я и привёл его в названии. Кроме того меньшая ошибка чем в других пакетах (проверял Maple,Mathcad b Matlab) при работе с вложенными функциями. А сама теория небесной механики (в её части) принадлежит Ландау Л. Д., спасибо тем кто это понимает.

maisvendoo
12.08.2018 17:49только, Python позволяет более точно отражать характер соотношений при численном интегрировании
Что позволяет...? Вот с этого места поподробнее, пожалуйста
А сама теория небесной механики (в её части) принадлежит Ландау Л. Д.
Чтоооо? Да как-то и до Ландау, знаете ли, открывали «Нептуны на кончике пера». Вы какую-то ересь несете, уважаемый гн. Тараненко
Scorobey Автор
12.08.2018 18:12+1В части параметрической формы представления орбит: Ландау Л. Д., Лифшиц Е. М. Курс теоретической физики. Механика. М.: Фю-матгиз, 1958.
Что касается численного интегрирования на Python читайте С. К. Буйначев Применение численных методов в математическом моделировании.
Не судите и судимы не будите.
Спасибо за комментарий.

maisvendoo
12.08.2018 18:24+1Что касается численного интегрирования на Python читайте…
Вот в этом и есть квинтэссенция моего неприятия Ваших публикаций. Вы излагаете очевидное, оставляя его очевидным. Вместо развернутого ответа на заданный вопрос (который можно было привести и в статье!) Вы тыкаете в источник, с которым я при желании могу ознакомится и без хабра.
Я вот на протяжении уже 60-й Вашей публикации хочу всё узнать, в чем соль применения питона и не получаю ответа на этот вопрос. Более точно отражает соотношения… Оставьте это для дипломных работ студентов, а здесь люди хотят конкретики
Как вообще универсальный ЯП может что-то отражать? Он отражает ровно то, что Вы заставляете его делать, написав программу, и не более того
Scorobey Автор
12.08.2018 18:53+1Конкретика состоит в решении конкретных задач.Все приведенные публикации решают конкретную задачу которая расширяет сферы использования языка. Неясно правда почему Вы считаете дипломные работы студентов уровнем ниже публикаций на ресурсе. Есть некоторые из них на очень высоком уровне. Откуда такое пренебрежение ???.. На ресурсе студентов больше половины и их интересами тоже нельзя пренебрегать.

maisvendoo
12.08.2018 19:11Вы-то явно не студент. Но как студент изъясняетесь — размыто, не конкретно. Что означает всё-таки
Python позволяет более точно отражать характер соотношений при численном интегрировании
Что вкладывается в понятие «более точно отражать характер соотношений при численном интегрировании»? Каким образом это связано с теми средствами, что предоставляет разработчику питон?

maisvendoo
12.08.2018 17:59Ах, да, не потрудитесь ли объяснить вот это

Как это, вместо гравитационного параметра Солнца сюда затесалось четыре пи в квадрате? Если это какое то нормирование, то интересна размерность переменных в приведенных уравнениях
Scorobey Автор
12.08.2018 18:23+1В математических моделях уравнения приводят к безразмерным параметрам.

maisvendoo
12.08.2018 18:29В математических моделях уравнения приводят к безразмерным параметрам
А так же и не приводятся, если в этом нет нужды
По отношению к чему выполняется нормирование координат и времени в этих уравнениях? Выкладки, которые провел я, вот сейчас на скорую руку не дают приведенной формы уравнений. Где источник выкладок, в котором можно убедится в верности приведенных соотношений?
Scorobey Автор
12.08.2018 18:37+1Правые части системы их трёх дифференциальных уравнений содержат одинаковый численный множитель что тут объяснять. Это изменяет только масштаб.

maisvendoo
12.08.2018 18:56+1Правые части системы их трёх дифференциальных уравнений содержат одинаковый численный множитель что тут объяснять
Людям, читающим данный ресурс, из соображений элементарной вежливости и уважения, принято объяснять многое, например так
Вывод безразмерных уравнений движения кометы

где tau — безразмерное время (в оборотах Земли вокруг Солнца); a — большая полуось орбиты Земли (а.е.); mu — гравитационный параметр Солнца
Scorobey Автор
12.08.2018 19:18+1Причём тут многозначительность и предметная область студен бы после изучения курса обыкновенных дифференциальных уравнений такой бы вопрос не задал. Ответ зависит от цели вопроса. Нельзя быть всегда правым и всё время тестировать и делать выводы. Я всегда отвечаю на содержательные вопросы а если Вы пытаетесь экзаменовать то это не Ваша функция.

maisvendoo
12.08.2018 19:26более точно отражать характер соотношений при численном интегрировании
Вот я и задавал вопрос содержательный, ответа не получил (сам дал ответ). Экзамен не сдан, да, и да, это моя функция, как полноправного члена данного сообщества
Хм, извините, вы пишите публикации на популярном общедоступном ресурсе, и если Вас спрашивают о содержании Ваших статей, об источниках выкладок, смысле параметров — извольте отвечать

c0f04
12.08.2018 19:48Вероятно, от Вас хотят услышать объяснения в отличии вычислений. В Python дробная часть вещественных чисел типа float ограничена 53 битами, а вот целые числа типа int не ограничены размером. Поэтому погрешность вычислений скорее всего будет примерно такой же, как и в других языках (но я сильно не интересовался этим вопросом в Python, могу ошибаться). Преимущества Python обычно в вычислениях с целыми числами.
Но есть возможность повысить точность с помощью классов Decimal и Fraction. Decimal хорошо воспроизводит точность для десятичных чисел, а Fraction может представлять числа в виде рациональных дробей. Но они крайне сильно повлияют на производительность, что для Вас не должно играть большой роли. Если ещё не используете их, рекомендую проверить разницу в точности вычислений по сравнению с float. Мне, по крайней мере было бы интересно.
DancingOnWater
12.08.2018 22:0553 бита на мантису? Т.е. 10 бит на порядок?

c0f04
12.08.2018 23:48Спасибо за интересный вопрос. По факту на мантиссу — 52. 53-й бит неявный и для нормальных чисел равен 1:
- IEEE_754 (см. binary64)
- Double-precision floating-point format
- Floating-point: “The leading 1 is 'implicit' in the significand.” — …huh?
Так что да, 11 бит на порядок, а не 10.
Но, как оказалось есть нормальные числа:
и денормализованные:
Например, 0 — денормализованное число, поэтому неявный бит у него должен смениться на 0.
Про нормальные и денормализованные числа до сего дня, признаться, не знал. По памяти я не помню, сколько в double на мантиссу выделяется, поэтому если б не спросили, я бы и не заметил подвоха.

DancingOnWater
12.08.2018 21:30+3А сама теория небесной механики (в её части) принадлежит Ландау Л. Д.
WTF??? Вы записали уравнение Кеплера от 1619 года.
Smbdy_kiev
13.08.2018 10:22Была взят учебник по теормеху. Очень занятное чтиво, признаться. Да только сами авторы учебника говорили, что это модель, и мы принебрегаем там, например, массой Земли относительно Солнца. Вернее не так. Берём ооооочень массивное тело, а вокруг него ооооочень немассивное. Ну и понятно, что это не отдельная теория Ландау и Лифшица. В общем, много неточностей. Да и не понятно, почему именно Python всех победил.

Victor_koly
13.08.2018 15:35Для 2 тел вполне хорошо работает понятие приведенной массы и все выражается через радиус-вектор между центрами масс тел (НЯП теор. физику, которую начал учить почти 10 лет назад именно с механики и именно в начале механики была задача 2 тел). Из сохранения момента импульса можем легче перейти к координатам (r, phy), правда зависимость от времени там выходит неявная. Как явно доказать, что выходит эллипс — не помню.
Конечно для задачи 3 тел так уже не выходит, т.к. 1 радиус-вектором ничего описать не выйдет.

homocomputeris
12.08.2018 16:49Для гамильтоновых систем нужно использовать геометрические методы интегрирования, а SciPy есть только многошаговые линейные методы.

DancingOnWater
12.08.2018 21:22не пробовали исследовать устойчивость построенных орбит?
Ответ известен давно: уравнения небесной механики неустойчивы по Ляпунову вдоль траектории, по нормали и бинормали все ок.

maisvendoo
13.08.2018 22:27не пробовали исследовать устойчивость…
Не пугайте Юрия Карловича такими страшными словами

kalbas
12.08.2018 17:03Смысл писать свой велосипед, если уже есть великолепнейший www.astropy.org

maisvendoo
12.08.2018 20:14+2Смысл может заключаться в попытках задуть это в уши Минобра. Автор широко взял разбег, и надолго, судя по уровню графомании на ресурсе. А потом мы,
боевые магидействующие преподаватели, страдаем от всяческих нововведений, инициированных подобными «популяризаторами».
iig
13.08.2018 10:39Ну, если вместо древних методичек с фортраном будут новые методички с питоном, не думаю, что хоть один преподаватель от этого пострадает. Хотя, прежде чем выкатывать свой велосипед, возможно, стоит поинтересоваться, что принято использовать для научных расчетов. Так то и на bash можно уравнения решать. Древние математики как-то даже без компьютера обходились.

maisvendoo
13.08.2018 14:54если вместо древних методичек с фортраном будут новые методички с питоном
В данном случае мне всё равно, какой инструмент пропагандирует автор. Любой инструмент в неумелых руках превращается в оружие массового уничтожения молодых умов. Меня возмущает наплевательский подход к фактическому материалу в предметной области, в данном случае в астрономии и механике. Молодежь будет гуглить и нагуглит вот это чтиво, где Луна вращается по окружности на расстоянии 38 млн. км от Земли. Это сродни той самой задачке про периметр прямоугольного треугольника со сторонами 3, 4 и 6 метров. Сбывается предсказание академика Арнольда (земля ему пухом) — в сферу высшего образования лезут дилетанты со своими дилетантскими воззрениями.
Так что фортран там или питон, значения не имеет. Я не против популяризации питона, я против его популяризации таким способом

Chupaka
12.08.2018 18:07Я на рисунке с орбитами Земли и Марса "круговую" орбиту Земли всё равно вижу довольно выразительным эллипсом. Если это популяризация Питона в области рисования окружностей, то она получилась так себе...

AlexPublic
12.08.2018 18:10+1Это не построение орбиты Земли, Луны, Марса и т.п., а какое упражнение в рисование окружностей на Питоне. Реальные орбиты не имеют ничего общего с этим. Для их построения требуется численно решить простейшую систему диф. уравнений второго порядка (я помнится делал подобное руками вместе с визуализацией на OpenGL ещё на 1-ом курсе в рамках лабораторной работы) — сейчас это делается пару строчек на scipy. И то это будет приближением, не учитывающим различные более тонкие поправки (типа ОТО, электромагнитных взаимодействий, гидродинамики и т.д.). Но уже неплохим приближением, как минимум рисующим нормальные эллипсы. А не показанная здесь ерунда с прорисовкой окружностей.

AlexPublic
12.08.2018 19:43Добавление.
Только сейчас заметил, что орбита кометы вычисляется вроде как методом численного решения диф. уравнений. Но опять же и тут получился полный бред. Потому как под системой уравнений я имел в виду не просто 3 пространственные координаты, а все участвующие в движение тела (т.е. 3*N уравнений должно быть) и учёт суммарной гравитационной силы (каждое тело в систем действует на всех остальных). А решать численно указанный пример — это тоже полная чушь, т.к. он элементарно решается аналитически. Т.е. если мы пренебрегаем взаимодействием тел между собой (хотя непонятно как это можно сделать в случае той же луны) и считаем только полёт в гравитационном поле солнца, то никаких численных интегрирований не нужно — уравнение решается аналитически в общем виде (получается тот самый эллипс).
Т.е. в итоге у вас в тех случая, где требуется численное решение системы диф. уравнений, его нет. А там где оно не нужно, оно есть. Феерично. )))
maisvendoo
12.08.2018 20:09А решать численно указанный пример — это тоже полная чушь, т.к. он элементарно решается аналитически
… в классической задаче двух тел
Такую задачу нужно рассматривать в контексте задачи N-тел, Вы совершенно правы, так как динамика кометы определяется возмущениями со стороны, например, планет-гигантов
Да Вы посмотрите на список статей данного автора — темы от небесной механики до ядерных реакторов. Что-то мне сомнительно, что один человек может быть абсолютно компетентен во всех этих вопросах

maisvendoo
12.08.2018 20:55+1решается аналитически
Позволю себе, однако, ремарку.
Нет ничего плохого в том, что человек берет аналитическую задачу и решает её численно, а потом пишет об этом статью. Это очень хороший и сильный прием, я сам часто таковой использую. Но статья должна быть не о том как мы решаем элементарную и давно решенную задачу, а о том, какие выводы мы извлекаем из процесса.
Например, для объяснения принципа построения численных методов решения задач на ЭВМ — нет ничего лучше взяв простую задачу с аналитическим решением разобрать процесс построения численной схемы по косточкам, прояснить нюансы, сравнивая получаемые результаты с известным аналитическим решением. Поиграть с параметрами численной схемы влияющими на точность решения, указать на способы её повышения. Просто, наглядно, не перегружает читателя лишними сущностями.
здесь же подобного не наблюдается. Здесь схема построения всех статей такова:
1. Ура! Питон умеет решать дифуры!
2. Берем процесс Х.
3. Решаем дифуру, описывающую процесс Х на питоне
4. Сдабриваем всё картинками формул, надергаными из книжек
5. Строим корявые графики
Выводы — да какие выводы! Зачем?! Один вывод — питон умеет решать ОДУ для процесса Х. Мы рады за Вас, мы сами давно знаем, что он это умеет.
AlexPublic
12.08.2018 21:23Позволю себе, однако, ремарку.
Нет ничего плохого в том, что человек берет аналитическую задачу и решает её численно, а потом пишет об этом статью. Это очень хороший и сильный прием, я сам часто таковой использую. Но статья должна быть не о том как мы решаем элементарную и давно решенную задачу, а о том, какие выводы мы извлекаем из процесса.
Только при этом довольно трудно обосновать зачем вообще понадобилось численно решение, т.к. аналитическое априори лучше и смысл у численного появляется только в случае невозможности аналитического. Если аудитория это хорошо понимает и воспринимает обсуждаемый пример исключительно как отработку неких технических приёмов, то тогда почему бы и нет…
здесь же подобного не наблюдается. Здесь схема построения всех статей такова:
1. Ура! Питон умеет решать дифуры!
2. Берем процесс Х.
3. Решаем дифуру, описывающую процесс Х на питоне
4. Сдабриваем всё картинками формул, надергаными из книжек
5. Строим корявые графики
На самом деле, если бы обсуждаемая статья была бы вот прямо такой, то я бы и слова против не сказал (ну да, наивно, но почему бы и нет). Но тут же всё совершенно по другому.
Тут большая часть статьи занята рисованием окружностей (называя их при этом орбитами планет)!!!
И только в конце есть небольшой пример численного решения диф. уравнения для кометы, но при этом почему-то без учёта взаимодействия с планетами (хотя именно в учёте этого взаимодействия и есть весь смысл использования численного решения системы диф. уравнений, а без него можно просто подсмотреть готовое аналитическое решение).
В общем дикая статья и видимо ужасно не образованный автор. Хотя заявляемую им изначальную цель (популяризацию Питона) я полностью поддерживаю. Но не так же убого это делать…

maisvendoo
13.08.2018 07:39+1Уважаемый господин Тараненко! Я официально заявляю Вам — вы пишете охинею. Если на другое ещё можно было закрыть глаза, то вот это
Созданный график позволяет расширить задачу и посмотреть какой будет орбита луны, если радиус орбиты Луны будет равен R2=3.844*10e7.
я пропустить уже точно не могу.
И так, Вы фантазируете на тему формы орбиты Луны, варьируя расстояние от Земли до Луны. Задаете радиус в 38,44 млн. километров. А вы в курсе существования понятия о сфере действия тяготения одного тела, относительно другого?
Давайте-ка посчитаем условный радиус сферы влияния Земли (m) относительно Солнца (M)
r = a * (m / M) ^(2/5) = 1,5e8 * (5.98e24 / 1.99e30)^(2/5) = 930000 км
930 тысяч километров! При решении ограниченной задачи трех тел можно считать что за этой границей Земля не притягивает Луну вообще! То есть, находясь на расстоянии в 38 млн. км. от Земля Луна превратится в планету Солнечной системы, а не спутник Земли и будет иметь совершенно другую траекторию. Согласно законам небесной механики, траектория Луны нарисованная Вами существовать не может
Так что мой Вам совет —
вот эту лажу

Victor_koly
13.08.2018 16:01Замечу, что в противоположную сторону (дальше по лучу «Солнце-Земля») расстояние будет немного больше, чем в сторону Солнца. Можно оценить более точно величины.
Центробежную силу я тут не учитываю (может у нас вовсе не подвижный спутник, а мы просто считаем силу действия гравитации на зависший относительно Солнца объект в некий момнет времени), но более точно выражение будет такое. Берем например случай афелия (обозначим буквой a, расстояние от Земли до тела — r), а массы Солнца и Земли — M и m.
Тогда нужно решить уравнение
m/r^2 — M/(a-r)^2 = 0 (случай нахождения тела на линии между Землей и Солнцем)
(M-m)*r^2 + 2am*r — ma^2 = 0
Вышло у меня что-то вроде такого:
r = a*sqrt(m)*(sqrt(M)-sqrt(m))/(M-m) = a*sqrt(m)/(sqrt(M)+sqrt(m)).
А вообще да, погрешность совсем небольшая и на Ваше замечание никак не влияет.
maisvendoo
13.08.2018 18:16Естественно, форма этой условной «сферы» весьма далека от сферической. Выяснение точной формы этой поверхности лежит за гранью практического смысла, для практических расчетов достаточно сферы с радиусом
r = a (m / M)^(2/5)
где a — расстояние между телами, m и M — массы соответственно большего и меньшего тела. Практически это применяется в так называемом методе сопряжения конических сечений для приближенного расчета межпланетных траекторий и оценки устойчивости орбит.

maisvendoo
13.08.2018 18:27+2Ну так на этом приключения статьи господина Тараненко не заканчиваются. Приведу листинги двух его программ
Определение орбит Земли и Луны при R2 = 3.844e5 кмfrom numpy import*
from matplotlib.pyplot import*
R1=1.496*10**8
T1=3.156*10**7
R2=3.844*10**5
T2=2.36*10**6
N=1000.0
def X(t):
return R1*cos(2*pi*t/T1)
def Y(t):
return R1*sin(2*pi*t/T1)
def x(t):
return R2*cos(2*pi*t/T2)
def y(t):
return R2*sin(2*pi*t/T2)
k=100
t=[T1*i/N for i in arange(0,k,1)]
X=array([X(w) for w in t])
Y=array([Y(w) for w in t])
x=array([x(w) for w in t])
y=array([y(w) for w in t])
XG=X+x
YG=Y+y
figure()
title("Траектория орбит Земли и Луны.\n Для положительных значений координат")
xlabel('X(t),XG(t)')
ylabel('Y(t),YG(t)')
axis([1.2*10**8,1.5*10**8,0,1*10**8])
plot(X,Y,label='Орбита Земли')
plot(XG,YG,label='Орбита Луны')
legend(loc='best')
grid(True)
show()

Victor_koly
13.08.2018 20:01+2Значит Луна вертится вокруг Земли на длинной палке.

maisvendoo
13.08.2018 21:22Вообще очень странно, и для меня удивительно, что такую туфту пишет выпускник мехфака УГХТУ, заведующий кафедрой.

Victor_koly
13.08.2018 21:38Гугл (и фото на аве) помог найти жителя моей страны, но может химики резко забыли физику.
P.S. Про заведующих не скажу, но преподы бывают совсем странные.
maisvendoo
13.08.2018 21:51но преподы бывают совсем странные.
Встречал я одного такого — величал себя доктором железнодорожных наук, написал письмо Медведеву (на тот момент президенту), что законы Ньютона неправильные. Доказывал, что силу можно переносить вдоль дуги окружности. Хотя человек очень уважаемый, но возраст и отсутствие занятости свое дело сделали. Грусно




kovserg
Вопрос не раскрыт: как по наблюдением за луной определить расстояние и периоды и потом сравнить с известными данными. Где описание систем координат. И главное практические вопросы не освещены: восход и заход луны и фаза луны, прилив и отлив и т.п. И зачем тут питон. Это всё наши предки умели задолго до питона и компьютеров.
ps: Почему нет ссылок на книжки по астрономии?
maisvendoo
Написана охинея. Луна движется по незамкнутой спирали, из-за того, что к Солнцу она притягивается в 2 раза сильнее, чем к Земле. Отсюда вытекает вращение узлов лунной орбиты с периодом ~18 лет и прочие известные нам эффекты, связанные с периодичностью лунных и солнечных затмений.
Чтобы это не было охинеей нужно оговорится: принимается допущение что Луна движется по окружности… и т.д.
В ту же степь
А ничего, что эксцентриситет земной орбиты равен 0,01671123?
Victor_koly
У Марса в 5.59 раз больше и автор решил пренебречь экс-м орбиты Земли в сравнении с орбитой Марса.
maisvendoo
Ради бога, но так и надо писать: «пренебрегаем...», «принимаем допущение, что… так как...». Так ведь нет же — с бухты барахты в статье утверждается — Земля движется по окружности
maisvendoo
Ещё шедевр
Шо, прямо декартовы координаты и определим? Телескопом? С экваториальной монтировкой?