
«Блюр» в простонародье — эффект размытия, в цифровой обработке изображений. Бывает очень эффектен и сам по себе, и как составляющее анимаций интерфейса, или более сложных производных эффектов (bloom/focusBlur/motionBlur). При всем этом честный блюр в лоб довольно медленен. И часто реализации встроенные в целевую платформу оставляют желать лучшего. То скорость печальна, то артефакты режут глаза. Ситуация рождает множество компромиссных реализаций, лучше или хуже подходящих для определенных условий. Оригинальная реализация с хорошим качеством достоверности и высочайшей скоростью, при этом нижайшей зависимостью от аппаратной части ждет вас под катом. Приятного аппетита!
(Laplace Blur — Предлагаемое оригинальное название алгоритма)
Сегодня мой внутренний демосценер пнул меня и заставил таки написать статью, которую нужно было написать уже полгода назад. Как любитель на досуге разрабатывать оригинальные алгоритмы эффектов, хотел бы предложить общественности алгоритм «почти гаусиан блюра», отличающийся применением исключительно быстрых процессорных инструкций (сдвигов и масок), а потому доступный к реализации вплоть до микроконтроллеров (чрезвычайно быстрый в ограниченном окружении).
По сложившейся у меня традиции написания статей на хабр, я буду приводить примеры на JS, как на языке максимально популярном, и хотите верьте хотите нет, очень удобном для целей быстрого прототипирования алгоритмов. К тому же, возможность реализовать это эффективно на JS пришла вместе с типизированными массивами. На моем не шибко мощном ноуте фулскрин изображение обрабатывается со скоростью 30fps (многопоточность воркеров задействована не была).
Данное описание присутствует здесь скорее для того, чтобы пояснить ход моих мыслей и догадок, которые привели меня к результату. Для тех кому будет интересно:
Оригинальная Функция Гаусса:
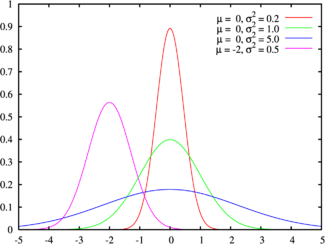
g(x) = a * e ** ( — ((x-b)**2) / c), где
а — амплитуда (если цвет у нас восемь бит на канал, то она = 256)
e — постоянная Эйлера ~2.7
b — сдвиг графика по х (нам не нужен = 0)
с — параметр влияющий на ширину графика связанный с ней как ~w/2.35
Наша частная функция (минус из показателя степени убран с заменой умножения делением):
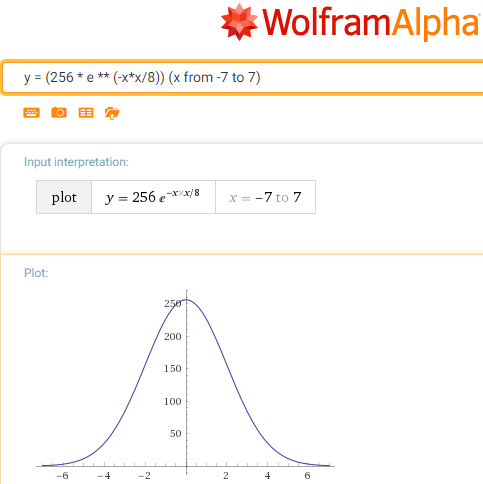
g(x) = 256 / e ** ( x*x / c)
Да начнется грязное аппроксимационное действо:
Заметим, что параметр c — очень близок к полуширине и поставим 8 (это связано с тем, за сколько шагов можно сдвинуть по одному 8 бит канала).
Также грубо заменим e на 2, отметив однако, что это влияет больше на кривизну «колокола» нежели на его границы. На самом деле влияет в 2/e раз, но сюрприз в том, что эта ошибка компенсирует внесенную при определении параметра с, так что граничные условия у нас все еще в порядке, а погрешность появляется лишь в слегка некорректном «нормальном распределении», для графических алгоритмов это будет сказываться на динамике градиентных переходов цветов, но это почти невозможно заметить глазом.
Итак, теперь наша функция такова:
gg(x) = 256 / 2 ** ( x*x / 8) или gg(x) = 2 ** (8 — x*x / 8)
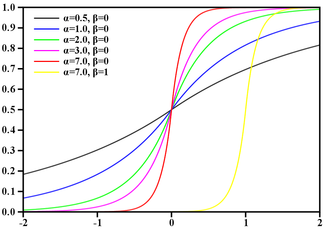
Заметим, что показатель степени (x*x/8) имеет ту же область значения [0-8], что и функция меньшего порядка abs(x), потому последняя является кандидатом на замену. Быстро проверим догадку, глянув как меняется график при ней gg(x) = 256/ (2 ** abs(x)):
GaussBlur vs LaplasBlur:
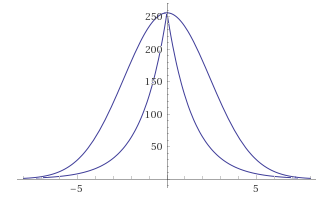
Кажется, отклонения слишком велики, к тому же функция, потеряв гладкость, теперь имеет пик. Но погодите.
Во первых, не будем забывать, что гладкость получаемых при размытии градиентов зависит не от функции плотности вероятности (коей является функция Гаусса), а от ее интеграла — функции распределения. На тот момент я этого факта не знал, но на самом деле, проведя «губительную» аппроксимацию относительно функции плотности вероятности (Гаусса), функция распределения при этом осталась достаточно похожей.
Было:
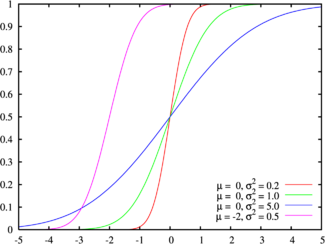
Стало:
Пруф, снятый с готового алгоритма, совпадает:
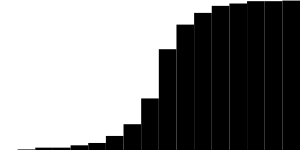
(забегая вперед скажу, что ошибка размытия моего алгоритма относительно Gausian x5 составила всего 3%).
Итак, мы перешли гораздо ближе к функции распределения Лапласа. Кто бы мог подумать, но им можно мыть изображения на 97% не хуже.
Пруф, разницы гаусиан блюра х5 и «Лаплас блюра» х7:

(это не черное изображение! Можете поизучать в редакторе)
Допущение этого преобразования позволило перейти к идее получения значения итеративной фильтрацией, к которому я планировал свести изначально.
Перед повествованием конкретного алгоритма будет честно, если я забегу вперед и сразу опишу его единственный недостаток (хотя реализацию можно исправить, с потерей скорости). Но данный алгоритм реализован с использованием сдвиговой арифметики, и степени 2ки являются его ограничением. Так оригинальный сделан для размытия х7 (что в тестах ближе всего соотноситься с Gausian x5). Связано это ограничение реализации с тем, что при восьмибитном цвете, сдвигая за шаг значение в накопителе фильтра на один бит, всякое воздействие от точки заканчивается максимум за 8 шагов. Я также реализовал чуть более медленную версию через пропорции и дополнительные сложения, которая реализует быстрое деление на 1.5 (получив в итоге радиус х15). Но с дальнейшим применением такого подхода погрешность растет, а скорость падает, что не позволяет его так использовать. С другой стороны, стоит заметить, что х15 уже достаточно, что бы не сильно замечать разницу, получен результат с оригинала или с даунсемплированого изоображения. Так что метод вполне годен, если нужна чрезвычайная скорость в ограниченном окружении.
Итак, ядро алгоритма простое, совершается четыре однотипных прохода:
1. Половина значения накопителя t (изначально равное нулю) складывается с половиной значения очередного пикселя, результат присваивается в него же. Продолжаем так до конца строки изображения. Для всех строк.
По завершению первого прохода изображение оказывается смазано в одну сторону.
2. Вторым проходом делаем то же самое в обратную сторону для всех линий.
Получаем изображение, полностью размытое по горизонтали.
3-4. Теперь делаем то же самое по вертикали.
Готово!
Изначально я использовал двухпроходный алгоритм с реализацией обратного размытия через стек, но он сложен для понимания, не грациозен, и к тому же на нынешних архитектурах оказался медленнее. Возможно, однопроходный алгоритм будет быстрее на микроконтроллерах, плюсом так же станет возможность выводить результат прогрессивно.
Текущий четырехпроходный способ реализации я подглядел на Хабре у предыдущего гуру по алгоритмам размытия. habr.com/post/151157 Пользуясь случаем, выражаю ему свою солидарность и глубокую благодарность.
Но на этом хаки не закончились. Теперь по поводу того, как вычислять все три канала цвета за одну инструкцию процессора! Дело в том, что использованный в качестве деления на два битовый сдвиг позволяет очень хорошо контролировать позиции бит результата. Единственной проблемой становится то, что младшие разряды каналов сползают в соседние старшие, но можно просто обнулить их, чем исправить проблему, с некоторой потерей точности. А согласно описанной формуле фильтра, сложение половины значения накопителя с половиной значения очередной ячейки (при условии обнуления съехавших разрядов) никогда не приводит к переполнению, так что беспокоиться за него не стоит. И формула фильтра для одновременного вычисления всех разрядов становиться такой:
buf32[i] = t = ( ( ( t >> 1 ) & 0x7F7F7F ) + ( ( buf32[i] >> 1 ) & 0x7F7F7F );
Однако требуется еще одно дополнение: опытным путем было выяснено, что потеря точности в данной формуле слишком значительна, визуально ощутимо прыгает яркость картинки. Стало понятно, что теряемый бит нужно округлять до целого, а не отбрасывать. Простым способом сделать это в целочисленной арифметике является прибавление половины делителя перед делением. Делитель у нас двойка, значит прибавлять нужно единицу, во все разряды, — константу 0x010101. Но с любым сложением нужно опасаться получить переполнение. Так что мы не можем использовать такую коррекцию для вычисления половинного значения очередной ячейки. (Если там белый цвет, мы получим переполнение, потому ее мы корректировать не будем). Но оказалось, что основную ошибку вносило многократное деление накопителя, который мы как раз скорректировать можем. Потому что, на самом деле, даже с такой коррекцией, значение в накопителе не поднимется выше 254. Зато при сложении с 0x010101 переполнения гарантировано не будет. И формула фильтра с коррекцией приобретает вид:
buf32[i] = t = ( ( ( ( 0x010101 + t ) >> 1 ) & 0x7F7F7F ) + ( ( buf32[i] >> 1 ) & 0x7F7F7F );
На самом деле формула достаточно хорошо выполняет коррекцию, так что при многократном повторном применении данного алгоритма к изображению, артефакты начинают виднеться только на втором десятке проходов. (не факт что повторение гаусиан блюра не даст подобных артефактов).
Дополнительно, есть замечательное свойство, при множестве проходов. (Являющееся заслугой не моего алгоритма, а самой «нормальности» нормального распределения). Уже на втором проходе Лаплас блюра функция плотности вероятности (если я правильно все прикинул) будет выглядеть как-то так:
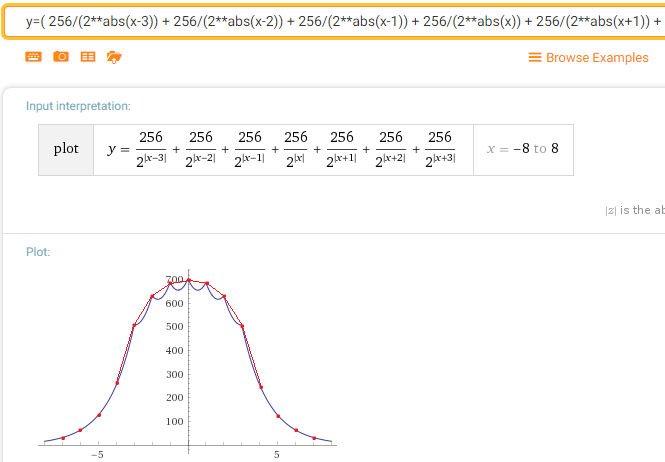
Что, согласитесь, уже очень близко к гаусиане.
Опытным путем я нашел, что использовать модификации с большим радиусом допустимо в паре, т.к. описанное выше свойство компенсирует ошибки, если последний проход является более точным (самый точный это описанный здесь алгоритм х7 блюра).
демо
реп
кодпен
Воззвание для крутых математиков:
Что было бы интересно узнать, насколько корректно использовать такой фильтр сепарабельно, не уверен получается ли там симметричная картина распределения. Хотя на глаз неоднородностей и не видно.
upd: Здесь буду поднимать полезные ссылки, любезно подаренные комментаторами, и найденные у других хабровчан.
1. Как работают intel мастера, опираясь на мощь SSE — software.intel.com/en-us/articles/iir-gaussian-blur-filter-implementation-using-intel-advanced-vector-extensions (спасибо vladimirovich )
2. Теоретическая база по теме «Fast image convolutions» + некоторые ее кастомные применения по отношению к честному гаусиан блюру — blog.ivank.net/fastest-gaussian-blur.html (спасибо Grox )
Предложения, комментарии, конструктивная критика — приветствуются!
Комментарии (35)

Grox
27.10.2018 16:38+7В статье не хватает выводов с ответом на ваши же вопросы «во сколько раз это быстрее, и стоит ли того потеря 1/32 точности.»

impfromliga Автор
27.10.2018 23:42Этот вопрос конечно гипотетический. Потому что даже если Очень строго подходить к оценке, считая например битовую сложность, или хотя бы реализовав на ассемблере и считая такты, остаётся контекст того, что это все таки апроксимация, а не чистый гаус, потому ответ будет в конечном счёте зависит от того отношения скорость/качество которое вы определите для своей задачи как достаточное

Grox
27.10.2018 23:53Тогда стоит хотя бы указать примерный %. Стоит ли вообще думать о таких апроксимациях, или это экономия на спичках?

impfromliga Автор
28.10.2018 00:29-2Поймите здесь не может быть простого ответа. И нет это не экономия на спичках. Но, возвращаясь опять к дисклеймеру важно заметить контекст в котором задача сравнивается. Наилучшее окружение для данного алгоритма (в котором его преимущество относительно растет) это простые инструкции. (отсутствие деления например и плавающей арифметики). Опять же это CPU алгоритм, его нет смысла сравнивать с GPU. (GPU наверняка будет быстрее). Хотя саму функцию фильтра можно перенести на float и на GPU. И возможно она там даже будет лидировать, но от данного алгоритма эта реализация уйдет очень далеко. Можно однако рассматривать его практически как вариант CPU постпроцессинга (как позиционирует Intel например свой алгоритм CPU АнтиАлиасинга MLAA — если не хочется тратить ресурсы GPU, можно помогать ему и постпроцеcсить на CPU)
upd: вот вы же указываете в профиле что писали на Spectrum 128K — должны бы понимать куда он как раз пригодиться. Ядро алгоритма очень простое, можете расчехлить спектрум и проверить.
Grox
28.10.2018 01:27Ну так можно же и на спектруме реализовать честного Гаусса. У вас отличная статья. Просто хотелось бы выводов и сравнений, как в этой статье. Но вы уже ответили ниже, чего вполне достаточно. А на спекки реализовать размытие изображений, только дразниться.

impfromliga Автор
28.10.2018 02:15только дразниться
В каком смысле? Думаете он не успеет? (Я просто по его скоростям и возможностям не шарю) Или имеете ввиду что под него уже ни кому не надо?
Во втором случае хочу немного заступиться, если не за спеку, то хотя бы за алгоритмы в целом. Сами по себе они в принципе бесполезны, но будучи реализованы под одно дают идеи и подходы, чаще всего переносимые под нужды. Хотя бы ради открытия/освежения этих идей и подходов они оправданы.
Grox
28.10.2018 02:36Z80 3,5МГц, 8 бит. Но дело не в этом. Там был экран 256 х 192, где пиксели в блоке 8 х 8 могли иметь только два цвета из палитры в 16 цветов.
Для примера


impfromliga Автор
28.10.2018 02:48+1Понял свою ошибку.
Ну теперь ради фана и желая идти до конца, — пишем Дизеринг-Блюр!
*иронично* Он может быть еще быстрее (Битовая сложность позволяет)
Grox
28.10.2018 17:36Учтите, в Z80 по сравнению с i8080 есть второй набор регистров, что довольно выгодно и другие улучшения.

impfromliga Автор
28.10.2018 00:09-1Иными словами, это вопрос к общественности, с целью услышать эмпирическую оценку, о том насколько более быстрым должен быть на ваш взгляд алгоритм, чтобы оправдать постерю точности в ~3%. Но и все равно, данная реализация обрабатывающая три канала за один проход, имеет ценой константный радиус. А если есть блавающая арифметика, и деление в ней быстрое, то радиус может быть разным. Скорость алгоритма в отрыве от железа возможно оценить только асимптотически, и здесь она О(4nm) или O(n*m) если делать однопроходно (но реализация с лучшей асимптотикой здесь медленнее, профессионал понимает что такое может случаться)
Так, что вы хотели конкретно спросить? Какую конструктивную критику здесь несёте.
На вашу постановку вопроса без критерия, абстрактный ответ в статье дан — это 97% эквивалент гауса с примерно втрое большей скоростью

DaylightIsBurning
28.10.2018 00:31А что на «обычном» железе с аппаратными операциями с плавающей точкой типа AMD x64 + SSE/AVX?

impfromliga Автор
28.10.2018 01:05На обычном железе типа AMD x64 ситуация прикидки на пальцах довольно неточна, в связи с тем, что современные настольные процессоры чрезвычайно усложнились в своем устройстве. Они пытаются угадывать условные переходы, выполнять инструкции параллельно, юзать L кеш, так что иной раз могут вообще выходить цифры будто инструкций выполняется больше чем максимальная частота процессора… а иногда нет.
Подробности на хабре уже писали тут: habr.com/company/otus/blog/343566
Чтоб замерить наверняка нужно писать бенчмарк, но отношения благодаря замене деления на сдвиг, и маски, вычисления без распаковки каналов по отдельности из int, будут примерно те же. Троекратное ускорение и больше. Вполне практично можно сделать процессинг на CPU если он слабо занят, для разгрузки видюхи.

Grox
28.10.2018 01:15«На вашу постановку вопроса без критерия» Это же вы поставили этот вопрос в самом начале статьи. Возможно, я был невнимателен, но про втрое большую скорость вижу ответ только здесь.
Если вы ставите вопросы перед написанием статьи, то стоит давать на них ответы вконце статьи. Даже если точных ответов нет.
impfromliga Автор
28.10.2018 02:08Неудобно мне как то давать столь не точные ответы на техническом ресурсе.
Но если вы настаиваете потеоретизировать на предмет прироста скорости на AMDx64
(снимаю с себя какую либо ответственность за дальнейшие размышления)
То предположив точной выдержку из habr.com/company/otus/blog/343566 о скорости инструкций:
Сдвиг ~1 такт (если автор статьи относил его к простым инструкциям)
Целое деление — 12-44 тактов (DIV/IDIV)
Float деление — до 37-39 тактов (FDIV)
SEE деление — 10-40 тактов
SEE умножение — 0.5-5 тактов
Можно предположить что мой выигрыш против CPU реализации гаусса отсюда habr.com/post/151157 (быстрее этой реализации я не видел, хотя она тоже аппроксимация, но не ограничено точная)
Там в центре стреляет такая функция:
 (Это если что, от инжинеров Intel software.intel.com/en-us/articles/iir-gaussian-blur-filter-implementation-using-intel-advanced-vector-extensions )
(Это если что, от инжинеров Intel software.intel.com/en-us/articles/iir-gaussian-blur-filter-implementation-using-intel-advanced-vector-extensions )
посчитав даже по минимому
4x SSE умножения = +4такта
2х сложения = +2 такта
2х вычитания = +2 такта
(игнорируя чтения которых тут больше, но предположим, что все попало в кеш)
= 8 тактов
х 3 канала
= 24 такта
против
2х сдвига = 2 такта
2х маскирование = 2 такта
2х сложение = 2 такта
= 6 тактов (все три канала сразу)
отсюда грязная оценка может быть даже выше х4 прирост относительно «intel-точного» гаус блюра, но с погрешностью 97% и для константного радиуса, зато с понижением требований к окружению исполнения (не требуется SSE, ни плавающей арифметики, ни даже деления, а уж маски и сдвиги и сложения есть везде)
Grox
28.10.2018 02:23Про AMDx64 спрашивал DaylightIsBurning

impfromliga Автор
28.10.2018 02:55(вопрос наверное забыл поставить)
Я его не знаю, у меня просто в закладках уже была хорошая статья, спросил только своего друга, красноглазого сишника, на предмет оценки ее валидности. Он сказал, что результаты похожи на то что он получал. Но в любом случае на это нельзя сколько нибудь строго опираться.
upd: а все понял. Ну просто вы тоже спрашивали про оценку, я решил ответить сразу в эту ветку (не думаю что я особо много тут комментариев соберу, тема то специфичная)

GeMir
28.10.2018 01:19+1А TeX вам тоже не близок?
$$f(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu^2)}{2\sigma^2}\right)$$

Ну и так далее. Очень уж вырвиглазные у вас формулы.
? — математическое ожидание, ?2 — дисперсия.

windrider
28.10.2018 02:20Как я понимаю, единственный способ увеличивать размытие – делать больше проходов? То есть, чем сильнее блюр, тем он (линейно) медленнее?
И еще нюанс с артефактами: если блюрить белый квадрат, края темнеют:

impfromliga Автор
28.10.2018 02:461.Увеличить размытие в данной реализации нет нельзя, это связанно со скоростным битовым хаком. Данный алгоритм для константного радиуса. Однако константа может быть х7 х15 х31 (однако учтите, что каждая следующая имеет большую погрешность 31 так тот вообще нежелательно использовать без дополнительного прохода х7), если интересно можете попробовать демо тут codepen.io/impfromliga/pen/VERzPJ блюр х7 х15 х31 прибинжен на клавиши 1,2,3
+ в принципе имеющихся уровней размытия достаточно чтобы если нужно больше получать даунсемплированием (масштабировать сжимая -> блюрить -> масштабировать увеличивая) т.к. пикселизация тем менее заметна глазу на картинках, чем более они размыты. (естественно есть потолок у такого способа) реализация такого блюра через даунсемплирование может быть сделано так же однопроходно (встроена в алг, чтоб ни чего не пережимать предварительно, и не тратя памяти и времени, слышал такая практика существует для облегчения шейдеров)
2.Края темнеют (это называется стратегия заполнения, фон за пределами растра считается черным, потому такое размытие вполне честно, стратегии бывают разные, можно поменять алгоритм под белый/серый цвет/ под взятие цвета с противоположной стороны/ под взятие ближайшего крайнего/ под медианку из некоторых пикселей в краевой зоне… по вашему вкусу)
— Здесь чтобы не перегружать суть алгоритма, стратегия была выбрана простейшая


Sabubu
А ваш алгоритм — это случайно не box blur, который используется в т.ч. в браузерах для размытия теней?
en.wikipedia.org/wiki/Box_blur
amritamaz.net/blog/understanding-box-blur
impfromliga Автор
По результату, совершенно нет. Суть бокс бобра как я понимаю в похожем архитектурно способе фильтрации изображения, но он эквивалентен единичной матрице свёртки, что очень примитивно. И даёт заметные квадратные паттерны размытия. Мой же даёт матрицу по распределению Лапласа, которое визуально очень близко к Гаусову. При этом для статичного радиуса х7 возможно доп ускорение на битовых
impfromliga Автор
Поправка, матрицы полностью состоящей из единиц (либо некоей одной константы обычно 1/кол-во элементов матрицы)
Sabubu
Ну ок. А давайте тогда про другой подвох спрошу: ваш метод ведь не учитывает нелинейность пространства sRGB? То есть условно, повышение значения RGB в 2 раза не означает повышения яркости пикселя в те же 2 раза.
aamonster
Эй-эй, так нечестно! Примерно все линейные фильтры делаются без учёта гаммы и т.п. (ещё по древнему-древнему фотошопу помню).
Хотя, возможно, имело бы смысл прогонять через LUT перед фильтром и через обратный после.
impfromliga Автор
Ну и еще надо уточнить. Конкретно для подтыкания коррекций в данную реализацию, скорее всего прийдется отказаться от ускоряющего хака с тремя каналами в одном int. Потому что для коррекции гаммы на вскидку int = LUT[int] будет недостаточно. Если мне не врет память коррекция гаммы связана с тем, что фактическое кол-во света от пиксела это квадрат (его площадь), а значения мы вычитаем линейно. Т.о. что бы без ошибок обрабатывать гамму, потребуется увеличивать битность каналов. (храня в HDR) Либо считать в один проход усложняя алгоритм.
Sabubu
Просто LUT тут маловато, надо расширять диапазон значений, не знаю, хватит тут 16 бит.
impfromliga Автор
aamonster меня опередил, коррекция гаммы в общем случае не относится к алгоритму свёртки/фильтру, она может быть добавленная отдельно к любому. Цветовые профили тоже отдельно реализуются. Сам гаус тоже коррекцию не включает по умолчанию.
Sabubu
Нет, коррекцией гаммы после применения фильтра это не решить. Надо преобразовать значения в линейные, применить эффект, преобразовать значения обратно в sRGB. И чтобы не потерять точность, может понадобиться преобразовать все из 8 в 16-бит (хотя я не уверен).
impfromliga Автор
Именно так как вы и пишите, не затрагивая сам блюр фильтр и можно добавить, только «после» сказали и тут же опровергли вы, а не я. Естественно коррекция на входе и выходе.
Про битность я уточнил как раз перед вами, habr.com/post/427077/#comment_19292437
(И тот факт, что это будет означать, что для удобной коррекции гаммы придется либо отказаться от 3х-канального хака, либо не повышая битность, терпеть большие погрешности)
Кстати для 64бит архитектур возможен качественный запил того же 3х канального хака только с int64 (просто на стадии коррекции понадобиться перепаковать)
Sabubu
> Кстати для 64бит архитектур возможен качественный запил того же 3х канального хака только с int64 (просто на стадии коррекции понадобиться перепаковать)
Ну сейчас все новые CPU 64-битные, мне кажется, стоит на это ориентироваться.
Кстати, вы не думали использовать SIMD-инструкции? Они умеют работать со 128 битами, и даже больше, за раз. То есть вы бы могли сдвигать, суммировать и делать AND сразу 4 32-битным значениям. А в более мощных процессорах по моему и 256 бит за раз можно обработать. Скорость должна получаться зверская. Они доступны в Си в виде функций и макросов.
Не знаю, можно ли их применить на горизонтальный проход, на вертикальный точно можно.
impfromliga Автор
SIMD — Отличная идея для «шейдерного» подхода под CPU, соседние строки/столбцы проходов являются независимыми, потому если оставлять хотя бы 2 прохода, можно. Но на горизонталях вопрос перепаковки (столбцов в строки) встает утяжеляя алгоритм (это даже если все попадает в кеш), так что прирост может на выходе захлебнуться. Надо проверять. В прочем ускорить только вертикальный проход так получиться.
На самом деле я уже пробовал вынимать из ARGB G в отдельный канал, зануляя его в исходнике, чтоб работать с запасом бит, но диже это оказалось медленнее. В исходном алгоритме итак предельно быстрые инструкции
Sabubu
А нельзя ли SIMD'ами оптимизировать именно горизонтальный проход?
У нас формула вида t1 = f(t0) + f(a), где a — старое значение пикселя, t0 и t1 — значения накопителя в разные моменты времени. Вычисление f(a) оптимизируется через SIMD:
— одновременно загружаем 4 соседних пикселя
— одновременно прибавляем 010101
— одновременно делаем сдвиг
— одновременно делаем AND
Остается из непараллельного только сложение с накопителем и обработка значений в накопителе — и то, может и тут как-то схитрить можно? Или переделать формулу? Чтобы мы копировали эти 4 пикселя в другой XMM регистр, сдвигали на 32 бита и складывали.
Что касается сборки пикселей из 4 соседних строк — вроде как тут описан способ загнать 2 32-битных регистра в XMM, может его можно на 4 регистра расширить?
Плюс, там кроме 128-битных есть ведь и 256-битные регистры (AVX). Это уже 8 пикселей за раз можно обрабатывать.
impfromliga Автор
Поканальное деление (на 2 с потерей бита) оптимизировать можно, но даленейшее вычисление зависимо через накопитель. Потому будет какой то оверхед на доп операции, какой — вопрос тестирования. Но может и получиться что то ещё выйграть. В любом случае гарантировано ускорить вертикальный проход в ~четверо было бы неплохо.
Но сейчас основным минусом Алга является константный радиус. Я думаю что возможно рассчитать более качественные константы для больших радиусов.