Классический пример системы с простыми правилами и сложным поведением — клеточные автоматы, именно на них я и ориентировался, пытаясь подобрать правила. Конечно же, для клеточных автоматов правила будут в большинстве случаев проще. Но частицы могут быть красивее!
Под катом много мегабайт гифок.
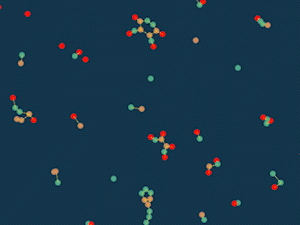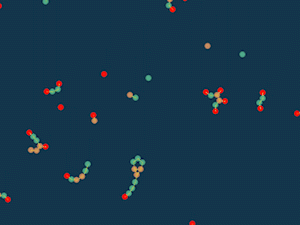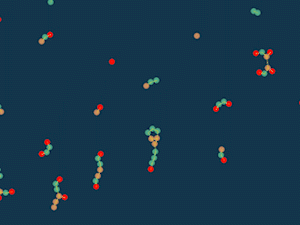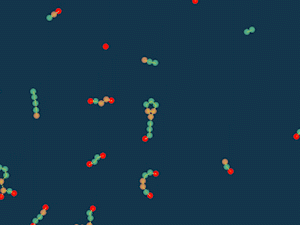
Клеточный суп
Сначала я пошёл по стопам игры «жизнь»: у каждой частицы есть счётчик “перенаселения”, который равен сумме обратных квадратов расстояний до других частиц. Если этот счётчик меньше определённого предела, то есть соседей мало, то частица притягивается к другим частицам, а если соседей много — отталкивается. Если частицы пересекаются, то они отталкиваются в любом случае, чтобы не проходить сквозь друг друга.
Случайно раскидываем частицы по полю и смотрим, что выйдет.

Интересно, что получается что-то похожее на клетки и выглядит уже довольно живо. Можно, например, добавить больше типов частиц. Пусть разные частицы будут по-разному увеличивать число соседей, а какие-то даже смогут его уменьшать.

Теперь наши “клетки” стали многослойными.
Минус подобных правил в том, что получаются довольно хаотичные не очень устойчивые структуры.
Поэтому идём дальше.
Игра в догонялки
Меняем правила игры. Больше не будем считать соседей. Пусть частицы будут просто притягиваться или отталкиваться в зависимости от их типов. Если все частицы одного типа, то тут всего 2 варианта: они либо все отталкиваются, либо все притягиваются.

Если есть больше типов частиц, то тут можно комбинировать, какие к каким будут притягиваться, а от каких отталкиваться.
Любое такое правило можно представить в виде матрицы N*N, где N — количество типов частиц, а в каждой ячейке либо притяжение, либо отталкивание. Притяжение обозначим за 0, а отталкивание — за 1. Тогда любая матрица соответствует определённому числу, например, матрица будет означать 0101, то есть 5 (последняя цифра в двоичном виде — первая в матрице). Количество различных матриц для правил равно . Например, для двух типов частиц получится 16 правил.

Может показаться, что правило 3 такое же, как правило 7, но если перевести их в матрицы, то получится и , а это значит, что в правиле 7 только бежевые притягиваются друг к другу. В то время как в правиле 3, бежевые притягиваются еще и к красным. Но из-за низкой плотности красных это оказывает малозаметный эффект. По-настоящему же одинаковыми правилами можно назвать, например, 3 и 12, так как всё поведение частиц идентично, только цвета поменялись местами. Если оставить только правила с уникальным поведением, то из 16 правил у нас останется 10. Для трёх типов частиц из 512 возможных комбинаций остаётся 104 уникальных, а для четырёх — 3044 из 65536 Получается последовательность 2, 10, 104, 3044.
Но вернёмся к нашим десяти правилам.

В глаза бросается правило 9, которое является матрицей , где одинаковые отталкиваются, а разные притягиваются. Случайно разбросанные частицы быстро образуют “нити” и на этом застывают.
Так же застывают правила 1 и 15: они эквивалентны двум единственным правилам для одного типа частиц (предыдущая анимированная гифка). Обычно застывают все правила, матрицы которых симметричны. Еще есть правила 2, 3, 5, и 11 с несимметричными матрицами. Это значит, что один вид частиц притягивается, ко второму, а второй отталкивается от первого. Начинаются “догонялки”.

Правило 3 слишком стабильное, в нём “догонялки” в какой-то момент прекращаются, а если и возобновляются, то редко и ненадолго. Правило 11 — слишком хаотичное. Остаются 2 и 5.
Можно их как-то скомбинировать, чтобы было еще интереснее. Я подобрал правило 105 для трёх цветов, то есть матрицу , и такое вот поведение:

Это всё выглядит живо, но неустойчиво. А как же определённые повторяющиеся “живые” существа? Как же поиск осцилляторов и глайдеров? Надо снова менять правила!
Плавающая жизнь
Не будем сильно менять правила. Вместо этого добавим новую фичу. Теперь частицы на небольшом расстоянии будут образовывать связи. Если частицы связаны, то они постоянно притягиваются друг к другу. Это притяжение не ослабевает с расстоянием. Но, если расстояние выше определённого порога, то связь рвётся.
Я попробовал разные варианты с тремя цветами и остановился на том, где красные могут образовывать только одну связь, бежевые — три, а голубые — две, то есть можно обозначить максимальные связи в виде .
При этом, красные не могут связываться с другими красными, бежевые и голубые могут иметь не больше двух связей с частицами своего цвета и не больше одной с частицами каждого другого цвета. Это всё в виде матрицы:

Я поигрался с разными правилами притягивания/отталкивания, и мне понравилось , то есть красные притягиваются к голубым, а во всех остальных случаях все отталкиваются.

Кажется, будто эти существа плавают в жидкости или машут крыльями.


Пара осцилляторов и пара глайдеров.
Неподвижные фигуры легко получить: нужно лишь не использовать красный и голубой вместе, так как в этих правилах это единственная комбинация с притяжением.


Но иногда движение возникает и при таких цветах. Некоторые фигуры начинают раскручиваться, отталкиваясь от других, получаются “шестерёнки”.

Заключение
В дальнейшем было бы интересно сравнивать полученные фигуры, собрать статистику по частоте их появления.
Еще можно эти правила использовать как основу для создания более сложных существ с едой, размножением, эволюцией.
Поиграть
Реализация на JS от v1vendi
Исходники
Код на Java
Похожие крутые штуки
Космики
Particle Life
Clusters
Комментарии (61)

pavel_kudinov
28.02.2019 19:54+2
Onigiri Автор
28.02.2019 23:36Действительно очень похоже. Я даже совсем недавно прочитал вашу статью, пока писал свою. Добавил еще на нее ссылку в конце.

Alonerover
01.03.2019 18:11Как вариант — добавить в ваш
«первобытный бульон»валентные связи, и станет можно моделировать молекулярную эволюцию.
habr.com/ru/post/374003

fivehouse
28.02.2019 20:01Прикольно. Но я думаю, что жизнь, или даже ее минимально адекватная модель, должна быть чем-то существенно большим, чем «интересным поведением». Да еще, если поведение было фактически отобрано вручную.
Есть такая тема современных исследований, как эволюция химических молекул еще до появления жизни, какой мы ее знаем. Иными словами ищут кирпичики жизни в несложной органической химии. Интересная визуализация достигнутого в этих исследований была бы очень полезной и поучительной.
k12th
28.02.2019 20:44+10Имеется ввиду игра «Жизнь» Джона Конвея, а не "способ существования белковых тел".

allcreater
01.03.2019 14:49Алгоритмы наподобие этого тем и интересны, что простые закономерности приводят к возникновению объектов со сложными свойствами. Если отбирать поведение вручную, это уже не то.

Sadler
28.02.2019 21:35+1Еще можно эти правила использовать как основу для создания более сложных существ с едой, размножением, эволюцией.
Да, генетика в этой работе прямо напрашивается. А ещё было бы интересно прикрутить какую-то примитивную нервную систему (сенсоры, проводники/нейроны, мышцы), которые позволили бы получить более сложное поведение даже на небольшом числе акторов.
opetrenko
01.03.2019 19:1610E14 атомов — в одной клетке человека.

Sadler
01.03.2019 19:23Я сомневаюсь, что стоит задача сделать реалистичную симуляцию на атомарном уровне или вообще приравнять эти абстрактные точки к реальным атомам, потому и говорю о функциях чуть более высокого порядка, за которыми было бы интересно наблюдать.

Janycz
28.02.2019 21:56+2Кажется, я начал понимать, как отдельные атомы начали образовывать молекулы, а молекулы — более сложные структуры. Хорошая статья.

Al_Azif
03.03.2019 06:59Есть ещё слаевская про «частицы на пальцах», интересная.
sly2m.livejournal.com/644080.html
По поводу симулятора — в теории можно попробовать симулировать законы обьединения, учитывая кол-во электронов на внешних орбиталях. То же самое, только в 3d.
По фану можно взять Houdini и написать там всю эту математику на VEX для частиц.
Тогда ещё и красиво посчитать можно будет.

Londoner
28.02.2019 22:05+2Вспомнил вот это.
В 2002 году Microsoft затеяла игру для программистов многих стран мира. ...Microsoft создала террариум. Всем желающим предложили населить его растениями и животными — травоядными и хищниками.
Программист задавал свойства существа (дальность зрения, максимальная скорость движения, сила атаки, сила защиты и т.п. — общая сумма была ограничена), алгоритмы его поведения (по какой траектории передвигаться; в каких случаях атаковать; есть все, что обнаружишь, или оставить немного на развод и т. п.). Трава росла. Травоядные ели траву. Хищники ели травоядных и друг друга.
Тот, кто больше ел, больше размножался. Задача состояла в том, чтобы размножиться как можно больше, вытесняя конкурирующие разновидности хищников, травоядных и т.п. Игра показала, что россияне плохо умеют изготовлять хищников, зато у них замечательно получаются травоядные. В ходе игры российские «коровы» победили всех конкурентов — за счет уникальной стадности и редкостного умения пакостить травоядным представителям других наций. По сути, российские разработчики были единственными, кто додумался, как сделать травоядных по-настоящему стадными. По правилам игры, животным не разрешалось напрямую обмениваться информацией. Поэтому, пасущаяся с краю стада «корова» не могла сообщить коллегам об увиденной «траве» или приближающихся хищниках.
Россияне придумали следующий алгоритм стадности. Если одна корова видела бегущую корову своего вида — она начинала бежать в том же направлении. Любопытно, что никто, кроме россиян, не додумался до такой идеи. По словам организаторов игры, именно эта не рассуждающая массовость принесла россиянам победу. Второе изобретение российских программистов было поизощреннее. Если в поле зрения их коровы не было травоядных своего вида — а сплошь чужаки, российская корова с максимальной скоростью съедала всю доступную траву, ничего не оставляя «на развод». И погибала от голода вместе с чужаками. Сложная смесь самопожертвования и ксенофобии.
Обратите внимание — жертвуя собой, отечественные травоядные боролись не с хищниками. Они мешали хорошо жить травоядным чужой породы. Конечно, не совсем правильно выводить национальную психологию из несложной разработки нескольких программистов — хотя бы и победителей крупного международного соревнования. Наверное, описанные выше свойства отечественных творений — не общий принцип. Но, возможно, достаточно показательная иллюстрация.

gekt0r
01.03.2019 16:49Считаю последний абзац достаточно оскорбительным

Londoner
01.03.2019 17:17Что именно Вас оскорбило?

gekt0r
01.03.2019 18:59… Конечно, не совсем правильно выводить национальную психологию из несложной разработки нескольких программистов… Но, возможно, достаточно показательная иллюстрация
Автор этих строк оскорбляет целую нацию, тонко намекая на их психологическую предрасположенность «мешать жить травоядным другой породы» (или другими словами «другим народам»). Ведь можно было подчеркнуть в конце именно неординарный способ решения задачи (в условиях которой вроде ничего не говорилось о морали). Ещё хуже то, что автор использовал во всей этой мысли слово «отечественный», что подчёркивает, что он является частью той нации, которую оскорбляет. Получается совсем неприятно.
Индуктивное рассуждение какое-то неуместное у автора тех строк

darkAlert
28.02.2019 22:24+7Есть целая книга «Designing Beauty: The Art of Cellular Automata» под редактурой Andrew Adamatzky. Там много подобной красоты.
Но меня, как человека написавшего диссертацию по теме клеточных автоматов, всегда расстраивает тот факт, что многие относятся к ним как к игрушке. Но клеточные автоматы это серьезная математическая модель, суть которой кратко — «сколь угодно сложное поведение пораждается наборами простых правил» (Стивен Вольфрам). Нейросети это также частный случай клеточных автоматов.
p.s. Никого не хотел обидеть, просто до сих пор вспоминаю отношение некоторых служителей науки, которые слышали термин «клеточные автоматы» и им на ум сразу приходило две вещи — «Жизнь» и «Игра». А у них мол там серьезное мат. моделирование, а вы тут со своими играми… Хотя мой бывший науч. рук рассказывал, что в когда она в 80ых защищалась, то там вообще чуть ли ее не в лженауке объвиняли.
firk
01.03.2019 00:20+1Но меня, как человека написавшего диссертацию по теме клеточных автоматов, всегда расстраивает тот факт, что многие относятся к ним как к игрушке. Но клеточные автоматы это серьезная математическая модель, суть которой кратко — «сколь угодно сложное поведение пораждается наборами простых правил»
Сложная математическая модель, суть которой — сделать себе хорошее развлечение. Ибо что может быть важнее этой цели? Все эти нейросети и т.п., если не прямо, то через несколько звеньев цепи тоже сделаны ради того, чтобы люди могли больше развлекаться.
Не надо это считать каким-то уничижительным признаком.

engine9
01.03.2019 00:21Ох какая милота.
Не совсем в тему, но напомнило игру powder game в ней прорва возможностей и всевозможных симуляций, от тепло- и электропроводности до возможности сгорать и распадаться с выделением частиц. Энтузиасты активно пилят разные интересные сцены, типа атомных реакторов или, например, симуляции электрических схем.
Yermack
01.03.2019 12:22Хотел было поправить, оказывается, такая игра тоже есть, а я вспомнил про Powder toy


Bismuth208
01.03.2019 19:31+3О, помню ее!
Делал там весьма компактный и мощный протонный лазер с фотонной накачкой водорода и титановыми рефлекторами! Странно то, что нигде такой конструкции не видел!
Save id:1358341
Принцип работы:
Фотонный генератор «PCLN + PHOT» испускает фотоны влево и в право, те что уходят налево преотражаются от двух полосок титанового отражателя (до сих пор не знаю, нашел ли кто еще этот баг/фичу).
Фотоны уходящие вправо проходят через разделитель среды “FILT” блока накачки/генератора с водородом «CLNE + H2».
Облученный фотонами водород распадается на протон «PROT» и электрон «ELEC».
Для поглощения избытка электронов и предотвращения детонации водорода используется поглотитель “PVOD”.
Те фотоны, что не распались отражаются от «HSWC» справа и снова проходят через «FILT», отражаются от титана и опять поступают в блок генерации/накачки (и так пока все не распадутся или время жизни фотонов не иссякнет).
Блок накачки/генерации находясь внутри блока нагревателя, подогревается для увеличения КПД. Перегрева водорода и титана не происходит, так как поступающие фотоны и водород успевают охладить начальную часть блока.
Сам нагреватель состоит из генератора плазмы, с которого тепло передается на алмаз «DMND», который передает тепло на «HSWC». Протоны спокойно проходят через последний и снимают тепло.
Собственно на выходе уже будет плотный пучок протонов разогретых до температуры близкой к плазме (~8000-9000).
Время выхода в рабочий режим <1с на core i5-4258U и очень низкая нагрузка на CPU во время работы.
Плавит почти все — мгновенно.
P.S. Цель была сделать компактно и мощно, а не максимально точно. Для повышения копийности в качестве нагревателя можно использовать газ «NBLE», который превращается в плазму при подаче разряда «SPRK».
P.P.S. Тогда мне хотелось играть с лазерами. Этот способ оказался безопаснее.

Kesha_kh
01.03.2019 00:25Результат внешне напоминает игру Cell Lab. Но там моделировалось именно поведение клетки, рост, деление и взаимодействие с другими клетками(поедание их или заражение своей ДНК)

red_andr
01.03.2019 00:41Забавно. Подумалось, что мы живём в одной такой клетке с одним набором правил, а рядом есть вселенные со всеми другими возможными наборами. Но им просто не повезло, что их правила не дают возможности образования таких устойчивых структур как молекулы и звёздные системы. И да, как вы уже поняли, я обожаю антропный принцип ;)

darkAlert
01.03.2019 01:03Космолог Макс Тегмарк высказал предположение, названное гипотезой математической вселенной, что любому математически непротиворечивому набору физических законов соответствует независимая, но реально существующая вселенная.

red_andr
01.03.2019 19:55Я бы даже скорее предположил, что параметры этих законов плавно меняются в пространстве.

shuhray
01.03.2019 01:10Вот один человек так лямбда-термы вычисляет
mathoverflow.net/questions/300273/what-is-chemlambda-in-which-ways-could-it-be-interesting-for-a-mathematician

Vsevo10d
01.03.2019 05:45Я бы все-таки не спешил, как вы и тут в комментариях предлагают, сравнивать это сразу с жизнью. Вы близки, но это только начало пути. Поясню развернуто.
Логика «эти притягиваются, а эти отталкиваются» реализуется наиболее наглядно на молекулярном уровне. Внутри любой молекулы атомы и их группы осциллируют, дрожат, поворачиваются, совершают пружинные и ножницеобразные движения. У каждой группы атомов при определенном соседстве есть такой строго определенный паттерн движений, достаточно хорошо описываемый. На этом эффекте основана вся инфракрасная спектроскопия. Даже небольшие и несложные молекулы — жирные кислоты, органические красители, олигосахариды — демонстрируют такие вещи, как полярность, различную гидрофильность/гидрофобность различных фрагментов и остатков (вспомним, что типичное поверхностно-активное вещество — это гидрофильная заряженная «голова» с гидрофобным углеводородным «хвостом»), сворачиваются в мицеллы. Эти их свойства активно используют для создания моющих средств, эмульгаторов, растворителей. Вещества со сродством к определенным субстратам используют как красители, защитные покрытия.
Дальше-больше: различные аминокислоты имеют разную гидрофильность и различный заряд, что определяет укладку цепочки самыми разнообразными формами, которые все же имеют ряд наиболее «удобных», энергетически выгодных. Так устроены все вторичные белковые структуры, основа самых главных биологических молекул. Все это из разряда «красный отталкивается от голубого и сворачивается в клубок вместе с зеленым».
А жизнь — это уже больше про: питательный субстрат, движение по градиенту концентрации питательного субстрата, хемоаттрактанты, движение за источником тепла/света и фазы фотосинтеза, трофность питания и простейшие биохимические циклы, многоклеточность и эмбриональные индукторы (почитайте про организатор Шпемана например).
То, что вы делаете — очень круто! Продолжайте, попробуйте создать развивающееся многоклеточное, как Марков, например (https://www.youtube.com/watch?v=LA1n6OTF5RI) или пищевую цепочку, как тут: habr.com/ru/post/336330, или автотрофов в среде с меняющимся газовым составом. Переходите от простеньких систем к настоящим живым!
Kirhgoff
01.03.2019 06:11Там выше уже пояснили, имеется в виду «жизнь» Конвея, а не способ существования белковых тел.

tbl
01.03.2019 08:54посмотрел код, сила притяжения или отталкивания обратно-пропорциональна квадрату расстояния между частицами (если между ними нет линка): 1/d2
Интересно было бы поизучать другие анизотропные потенциальные поля, у нас в институте была подобная лаба по компьютерному моделированию частиц, мне попалось задание про поле, в котором взаимодействие частиц было пропорционально sin(?x + ?)/x2. Тоже интересные структуры появлялись.

kablag
01.03.2019 09:39Мне это напомнила вот эту старую игру www.swimbots.com.
В ней реализованно
более сложных существ с едой, размножением, эволюцией.

Kyushu
01.03.2019 11:32Полный восторг.
Сколько частиц можно взять чтобы эта молекулярная динамика работала в реальном времени?
tbl
01.03.2019 12:01до 500 на CPU 15-летней давности обсчитывалось норм в рантайме без рывков, а если на GPU обсчитывать (а расчеты параллелятся хорошо), и сразу же через него отображать, то я думаю, что до 10 миллионов спокойно дожать можно.

Kyushu
01.03.2019 12:25Что хорошо параллелятся согласен, но все же число вычислений пропорционально квадрату числа частиц, хотя сэкономить всегда можно. Срочно переводим в 3D — что, в общем-то совсем не сложно, садимся в трансгалактический аппарат и летаем по разным частям вселенной, отличающимися различными матрицами взаимодействия. Не забываем отослать заявку в 20th Century Fox на для анимации фантастического боевика. Эх, жалко своих дел по горло.

Sadler
01.03.2019 13:02+1Не нужно считать силы взаимодействия в разных частях галактики, достаточно определиться с максимальным расстоянием между взаимодействующими объектами, и можно свести задачу к разбиению пространства, что уже O(log N).

helgisbox
01.03.2019 12:05Прекрасная работа! Когда-то, лет 15 назад тоже нечто подобное делал, только добавил еще на расстояниях меньше радиуса частиц силы отталкивания. При достижении блоком частиц определенной массы они слипались. У вас, как я понял — просто гасится энергия при столкновении (нет отталкивания и нет пролета сквозь). И расцветку-яркость менял в зависимости от кинетической энергии частицы в заданном поле. Но вот по поводу того, что можно несколько цветов сделать для разных типов частиц не придумал.
Надо будет поэкспериментировать. Такие демонстрации являются своеобразными игрушка для нас — программистов ;) Сидишь — играешь с законами своего мира, и получаешь необычный результат.

dfgwer
01.03.2019 13:41+1Пробовали варьировать начальную температуру? И трение поставить на 0, тогда теоретически любая конфигурация будет двигаться вечно.

Zoolander
01.03.2019 16:12+3Создателям клеточных автоматов может пригодиться еще один правило — из живой природы, от настоящих «клеточных автоматов»
Ученые долго не могли понять способности инфузорий-туфелек обучаться. Было давно известно, что при попадании в неблагоприятную среду это одноклеточное существо как бы запоминает это зону и старается держать от нее подальше.
Кроме того, туфельки оказались способны запоминать, какие частицы съедобны, а какие нет. Ученые бросали им смесь разных частиц. Сначала подопытные глотали все подряд, но потом они выбирали только съедобные.
Более того проводились такие опыты — брали пробирку, одну часть освещали, а другую нет (парамеция-туфелька умеет различать освещенность). При заплыве на «неправильную» территорию ученые пропускали сквозь воду микроимпульс тока — не смертельный, но неприятный. Через некоторое время инфузории, рандомно плавающие туда-сюда, перестали заплывать на «опасный» участок. Более того, было видно, что они разворачиваются до того, как пересекут границу освещенности.
Несколько десятилетий подряд исследователи ставили все новые и новые опыты и приходили в восторг от способностей одноклеточных. Эти эксперименты ставили под сомнение сам факт, что для обучения нужен хоть какой-то мозг или хотя бы специализированные нервные клетки (которые появляются толкьо у многоклеточных).
Поскольку это комментарий под статьей о клеточных автоматах, вы уже можете догадаться, какое правило использовали парамеции туфельки.
Действительно, мозг для этого правила был не нужен.
Правило обучающихся туфелек1. Инфузории при попадании в неблагоприятные условия выбрасывают тучи стрекательных палочек.
2. При любом контакте со своими стрекательными палочками — они стремятся покинуть территорию.
Отмечу, что это правило можно отнести к условному классу алгоритмов «пометка территории». Если добавить в клеточные автоматы еще один класс специальных клеток, которые
— не препятствуют движению
— вызывают «желание» у хозяев покинуть территорию
— выбрасываются хозяевами в определенных ситуациях
— не визуализируются в дефолтном режиме — для пущего эффекта у наблюдателя
то мы получим «обучающийся» клеточный автомат, структуры которого будут стремиться избегать участков, где пострадали они или другие структуры предыдущего типа.
v1vendi
01.03.2019 16:43+1Нагло переписал Вашу реализацию на JavaScript :)
v1vendi.github.io/particle_automata
troll_face
01.03.2019 22:01О, спасибо, хоть посмотрел. Правда, Ваша реализация CPU грузит реально «нипадеццки» ;)

v1vendi
02.03.2019 14:03Там довольно забавная ситуация, рендеринг занимает даже больше ресурсов, чем расчёт элементов

troll_face
01.03.2019 18:12Onigiri, Вы бы добавили в README.md на гитхабе инструкцию, как запустить Вашу программку? Думаю, что и ссылка на рабочий апплет (GitHub дает github.io для хостинга, если не ошибаюсь), будет не лишней.
P.S. Еще туда неплохо бы добавить минимальное описание в README.md; если совсем лениво, вставьте ссылку на эту статью (и on English через google translator) ;)

Sk0rpion
01.03.2019 18:12Несколько месяцев назад смотрел описание устройства такой «жизни» на ютуб.
youtu.be/Z_zmZ23grXE
Тем не менее статья отличная, спасибо!

ivanggr
01.03.2019 18:12Почему бы не написать статью в журнал из перечня ВАК? Поработать с источниками — и вперед.

mickvav
01.03.2019 19:26Если у вас покояшиеся объекты начинают раскручиваться, значит ваш код не сохраняет энергию. Консервативную схему применить не пробовали?

Onigiri Автор
02.03.2019 10:49Да, но с сохранением энергии гораздо сложнее будет подобрать красивое поведение. Поэтому, допустим, что энергия незаметно поступает извне :)


podivilov
Но это же просто потрясающе!