Расшифровка видеозаписи лекции.

Теория игр — дисциплина, которая прочно зависла между математикой и социальными науками. Одним канатом к математике, другим канатом — к социальным наукам, прочно прикреплена.

В ней есть теоремы, достаточно серьёзные (теорема существования равновесия), про неё снят фильм «Игры разума», теория игр проявляется в множестве художественных произведений. Если смотреть вокруг, то и дело встречаешь игровую ситуацию. Я собрал несколько сюжетов.

Все мои презентации делает жена. Все презентации могут свободно распространяться, я буду крайне рад, если вы по ней будете читать лекции. Это полностью свободный материал.

Некоторые сюжеты спорные. Модели могут быть разные, можете не соглашаться с моей моделью.

• Теория игр в Талмуде.
• Теория игр в русской классике.
• Телеигра или задача о парковочных местах.
• Люксембург в Евросоюзе.
• Синдзо Абэ и Северная Корея
• Парадокс Брайеса в Метрогородке (Москва)
• Два парадокса Дональда Трампа
• Рациональное безумие (снова Северная Корея)

(В конце поста — опрос про бомбу.)

Талмуд: задача о наследстве

Когда-то было разрешено многоженство (3-4 тыс лет назад). Еврей, когда женился, подписывал брачный договор, сколько выплатят жене, когда он умрет. Ситуация: умирает еврей у которого три жены. Первой завещалось 100 монет, второй — 200, третьей — 300. Но когда открыли наследство, там было меньше 600 монет. Что делать?

Офтоп про подход евреев к решению вопросов:

Шаббат начинается с первой звездой. А за полярным кругом?

1. «Спуститься» по меридиану и ориентироваться по той местности где всё нормально. (не работает с Северным полюсом)
2. Начинать в 00-00 и не париться. (тоже не работает с Северным полюсом), поэтому:
3. Еврею нечего делать за полярным кругом и ездить туда не надо.

1. В Талмуде написано, если наследство меньше 100 монет, то делить поровну.
2. Если до 300 монет, то делим 50-100-150
3. Если 200 монет, делим 50-75-75

Как эти три условия можно склеить в одну формулу?

Принцип, как решать кооперативные игры.

Выписываем претензии каждой жены, претензии пар жен, при условии, что третья всё «погасила». Получаем список претензий, не только единичных, но и «компаний». Берется такое решение, такое разделение наследства, чтобы самая тяжелая претензия была минимально возможной (максимин). В теории игр это изучали, назвали "нуклеолус". Роберт Алман доказал, что все три сценария из Талмуда — строго по нуклеолусу!

Как это может быть? 3000 лет назад? Ни я, никто другой не понимает, как это может быть. (Господь диктовал? Или их математика была намного сложнее, чем мы думаем?)

Николай Васильевич Гоголь

Ихарев. Позвольте вам сделать один вопрос: как поступали вы доселе, чтобы пустить в ход колоды? Подкупать слуг ведь не всегда можно.

Утешительный. Сохрани Бог! да и опасно. Это значит иногда самого себя продать. Мы делаем это иначе. Один раз мы поступили вот как: приезжает на ярмонку наш агент, останавливается под именем купца в городском трактире. Лавки еще не успели нанять; сундуки и вьюки пока в комнате. Живет он в трактире, издерживается, ест, пьет — и вдруг пропадает неизвестно куда, не заплативши. Хозяин шарит в комнате. Видит, остался один вьюк; распаковывает — сто дюжин карт. Карты, натурально, сей же час проданы с публичного торга. Пустили рублем дешевле, купцы миг расхватали в свои лавки. А в четыре дни проигрался весь город!

Это чисто теоретико-числовая двухходовка. У меня тоже была недавно в жизни двухходовка, в Тюмени. Еду в поездом. Я изучаю ситуацию и прошу взять мне верхнее место в купе. Мне говорят: «Не надо экономить, берите нижнее, деньги не вопрос». Я говорю: «Верхнее».

Почему я просил верхнее место? (Подсказка: задачу я выполнил на 3/4)

Пришло время поиграть

Вот написан мой телефон. В самом телефоне нет ни одной непрочитанной смски, звук выключен. В течение минуты вы либо посылаете смс, либо не посылаете. Шоколадку получат те, кто послал смс, но только в том случае, если пославших будет не больше двух. Время пошло.

Минута прошла. 11 смсов:

• Шоколадка!
• Шоколадка
• Изи
• Шшшш
• 123
• Здравствуйте Алексей Владимирович
• Здравствуйте Алексей
• Шоколадка:)
• +
• Combo-breacker
• А

В Майкопе у меня на лекции был глава республики Адыгея и задал содержательный вопрос.

В Красноярске в зале сидели 300 мотивированных школьников. 138 смсов. Я начал их зачитывать, пятый оказался матерным.

Давайте разберем эту игру. Конечно это лохотрон. Ни разу за историю розыгрышей (ближе к 100 раундов) не было, чтобы шоколадка кому-то досталась.

Есть равновесия, когда зал договаривается на каких-то двух людей. Договор должен быть таким, в котором всем выгодно участвовать.

Равновесие — это такой розыгрыш, когда можно объявить стратегии вслух, и от этого они не поменяются.

Пускай шоколадка в 100 раз дороже смса (если в 1000, то результат будет немножко другой). Количество людей в зале не играет почти никакой роли.

Смешанные равновесия. Каждый из вас сомневается и не знает как играть. И он отдает свой ход случаю. Например, рулетке 1/6. Человек решает, что в 1/6 случаев (при многократной игре) он будет посылать смс.

Вопрос: какая «рулетка» будет равновесной?

Мы хотим найти симметричное равновесие. Раздаем всем рулетку 1/р. Надо удостовериться, что люди хотят в такую рулетку сыграть.

Существенная деталь. Если вы её поймете, считай что с теорией игр вы уже познакомились. Я утверждаю, что с равновесием совместимо только одно «р».

Предположим что «р» очень маленькое. Например 1/1000. Тогда получив такую рулетку ты быстро догадаешься, что шоколадки не видать и выкинешь такую рулетку и будешь слать смс.

Если «р» слишком большое, например 1/2. Тогда правильным решением будет не посылать смс и сэкономить рубль. Точно ты не будешь вторым, а скорее всего сорок вторым.

Есть расчет равновесии с одновременным глубоким продумыванием. Но сейчас не о них речь.

Значения «р» должны быть такие, что ваш выигрыш от того, что вы пошлете смс, в среднем будет равен выигрышу от того, что не пошлете.

Посчитаем эту вероятность.

N+2 — количество людей в аудитории.


На видео разбор формул на 33й минуте.

(1+pn)(1+p)^n = 1/100 (вероятность шоколадки=цене смс)

Если рулетка такова, что её независимый запуск всеми остальными участниками приводит к вероятности получения шоколадки в случае вашего отправления смса (равной 0,01).

При цене соотношении цен шоколадка/смс = 100, количество смс будет 7, при 1000 — 10.

Вы видите, что коллективная рациональность страдает. Мы ищем равновесие, когда каждый ведет себя рационально, но как исход, почти наверняка будет смсок больше. Только сговор даст больше результата.

Один из результатов теории игр — идея свободного рынка, что он сам всё наладит — совершенно не верна. Если пустили на самотёк — будет хуже, чем если бы договорились.

Люксембург в Евросоюзе

Приготовились смеяться.

Люксембург входил в Евросоюз.

Совет министров Европейского союза состоял из 6 представителей по одному из каждой страны ЕС (с 1958 по 1973).

Страны были разные и поэтому:

• Франция Германия Италия — по 4 голоса,
• Бельгия, Нидерланды — 2 голоса,
• Люксембург — 1 голос.

Шесть человек принимали решения по всем вопросам 15 лет подряд. Решение принято, если квота достигнута или превзойдена (больше либо равно). Квота = 12…

Не существует ни одной потенциальной ситуации, когда Люксембург может изменить ход решения своим голосом. Сидит человек 15 лет за столом и ничего никогда не решает.

Я когда это узнал, попросил своих знакомых немцев (не было знакомых из Люксембурга) прокомментировать. Они ответили:
— Ты не сравнивай Люксембург с вашим советским лагерем, где математику хорошо знают. Они никакого представления о четности/нечетности не имеют.
— Как, вся страна?!??!?
— Ну да, кроме, может, парочки учителей.

Спросил ещё одного немца, который женат на люксембуржке. Он сказал:
— Люксембург — это страна, которая полностью аполитична, и вообще не следит за внешней политикой. В Люксембурге людей интересует только то, что происходит у них во дворе.

Синдзо Абэ

Я ехал на лекцию по теории игр и увидел новость:


У меня заиграл тревожный звоночек. Что этого не может быть. Никак. КНДР способны сделать атомную бомбу, но доставить её — вряд ли.

Зачем вводить в намеренную дезинформацию?

Правда в том, что ракеты могут долететь до Японии. Это страшно для японцев. Но если это сообщить НАТО, это ни к чему не приведет, а пугая «Европой» — приведет.

Я не настаиваю на правоте, может есть и другие анализы этой новости.

Метрогородок

Когда-то давно шутники назвали улицу «Открытое шоссе», потому что она тупиковая и упирается в лес. Те же шутники назвали район «Метрогородок», потому что там никогда не будет метро."

В начале 90х пробок еще не было и разыгрался следующий сюжет.


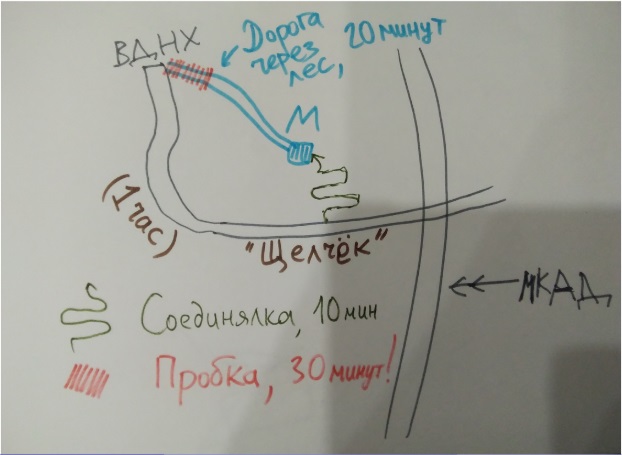
Метрогородок обозначен буквой «М».

Щелковское шоссе соединяет гигантский кластер городов. 700 000 человек, согласно последней переписи.

Из Метрогородка к ВДНХ ведет маленькая извилистая дорожка, без единого светофора. По шоссе ехать час, по дорожке — 20 минут. Часть народа с шоссе начинает «срезать» — результат — 30 мин пробка.

Это точно из теории игр. Если сильно меньше 30 минут пробка — это известно, и тогда еще больше машин сворачивают, чтоб «срезать». Если сильно больше, народ перестает «срезать».

Равновесное значение времени пробки — чисто результат теоретико-числового взаимодействия автомобилистов, которые принимают решение куда ехать. Принцип Вардропа.

Для водителей как был час, так и остался, а для жителей Метрогородка 20 минут превратились в 50. Без «соединялки» 1 час и 20 минут, с «соединялкой» — 1 час и 50 минут. Чистый парадокс Браеса.

А вот пример который стоил премии Данцига. Юрий Евгениевич Нестеров получил высочайшую награду в области математического программирования.

Идея такая. Если появление новой дороги может привести к ухудшению дорожной ситуации, то, наверное, какой-то запрет может привести к улучшению. И Он изобразил конкретику, когда это происходит.

Есть пункт «А» и пункт «Б» и посередине точка, которой нельзя избежать.


В итоге все едут 1 час и 20 минут. Нестеров предложил поставить знак «смены дороги».
В итоге машины поделились на две категории, кто ехал прямо, а потом в объезд (4000) и тех, кто ехал в объезд, а потом прямо (4000) и при этом пробок на узкой прямой дороге не возникало. И в итоге все участники дорожного движения едут 1 час.

Трамп

За Трампа проголосовало меньше, чем против него.

Выборщики.


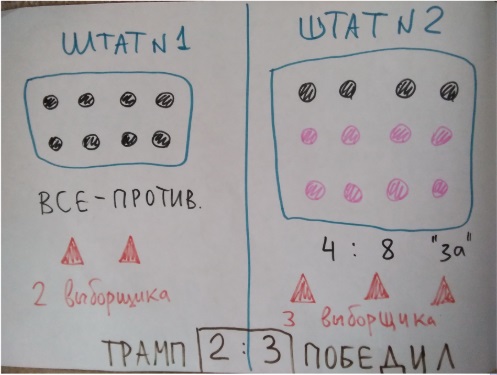
В первом штате 8 млн чел, все «против» Трампа. 2 выборщика.
Во втором штате 12 млн чел, 8 — «за», 4 — «против». 3 выборщика и все обязаны голосовать за Трампа.
В итоге 2:3 по выборщикам в пользу Трампа, хотя за него проголосовало 8 а против него 12 млн.

Скандальный кандидат

Бывает, что какой-то кандидат по опросам не проходит. Или про «Брекзит» по опросам не должен был произойти. Есть недоброкачественные опросы (когда выпиливают неугодные мнения из выборки), но профессиональные социологи так делают редко.

Человек живет как будто в кафтане, говорит одно, а перед урной сбрасывает кафтан и голосует по-другому. В кафтане удобно жить, у него есть некое социальное окружение: работодатель, семья, родители.

Вот модель моего знакомого, потому что у меня нет фейсбука. Все эти люди, так или иначе, на него влияют.


Мнения 500 человек важны. И если мы с ним обсуждаем политику и сильно расходимся, это представляет некоторую небольшую дискомфортную составляющую.

Модель социального раскола.

Примеры:

• Брекзит
• Русско-украинский раскол
• Выборы США

Есть люди, которые принципиально не участвуют в спорах, это их позиция, не потому что у них нет своего мнения, а потому что издержки от выражения своей точки зрения очень велики.

Можно написать функцию выигрыша:


Есть матрица взаимодействий a_ij (много миллионов на много миллионов). В каждой клеточке написано, как каждый человек на каждого влияет и с каким знаком. Сильно несимметричная матрица. Один может влиять на очень многих, но на одного влияют человек 200.

Мы умножаем внутреннее состояние v_i человека на то, что он сказал вслух ?_i.

Равновесие — это когда каждый принял решение, какое ? транслировать вслух.

Могут даже думать одновременно про одно, а вслух говорить одновременно другое. Оба врут, но солидаризируются.

Еще добавляются шумы. И вычисляется с какой вероятностью вы промолчите, скажете «за» или «против». На этот набор вероятностей возникают уравнения.


С пассионарных и фанатиков надо начинать просчитывать равновесие.


Телевизор — это магнитное поле, которое смещает внутреннее мнение.


Вероятность того, что вы будете топить «за» какую-то конкретную сторону, равна вероятности того, что разница белых шумов будет больше, чем выигрыш. Всё определяется значением внутри скобок, а это получается в зависимости от остальных. В итоге система уравнений.

При формуле моделирования белого шума:


Получается по два уравнения на каждого человека, 100 млн человек — 200 млн уравнений. Очень много.

Возможно, настанет момент, когда можно будет взять данные соцопросов, исследовать количественные показатели социальной сети знакомств и сказать: «В этой системе соцопрос на 7% снизит количество голосов за данного кандидата.»

Теоретически это может быть. Я не знаю сколько будет препятствий на пути туда.

Выводы

Люди стесняются своей поддержки «скандального» кандидата (Жириновский, Навальный и т.п.), но у избирательной урны «дают выход протесту». Решив эту систему уравнений, мы смогли бы количественно оценить отклонения результатов опросов от результатов реального голосования. Но нам мешает сложность устройства социальных сетей.

Модель рационального безумия

Многие люди поражаются «бесстрашию» руководства Северной Кореи, проводящей испытания своего ядерного оружия «под носом» у США. Особенно, учитывая судьбу Каддафи, Саддама Хусейна и др. Неужели Ким Чен Ын сошёл с ума? Однако в его «безумном» поведении вполне может быть рациональное зерно.

Это модель Цезаря, сжигающего мосты.


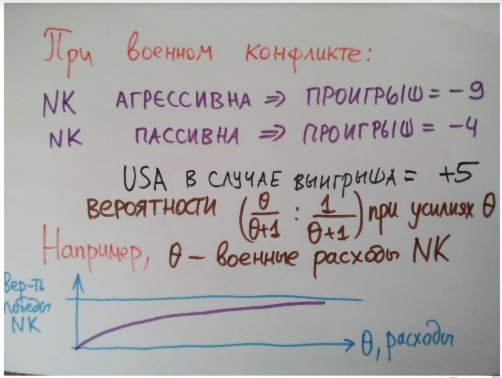
В случае войны, страну с ядерным оружием уничтожат полностью. Если у нее нет ядерного оружия, можно победить и без полного уничтожения. Если руководитель страны знает, что «либо пан, либо пропал», то на войну будут пущены огромные ресурсы. А если так, то противоположная сторона испугается этих больших ресурсов, потому что у неё самой будет большой проигрыш от войны.


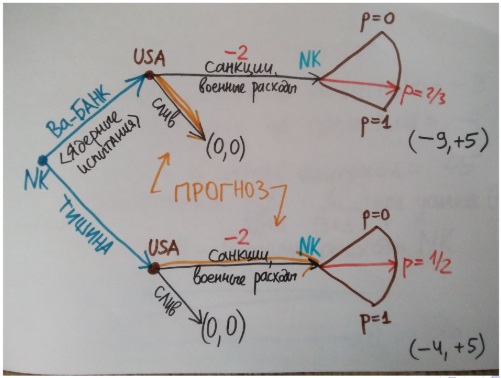
Дерево игры и прогноз.

P.S.

Поднимите руку, кто считает что в ближайшие пять лет будет скинута атомная бомба?
Я считаю 50%. Пол руки бы я поднял.