Научно-исследовательская работа, пожалуй, самая интересная часть нашего обучения. Идея в том, чтобы ещё в университете попробовать себя в выбранном направлении. Например, студенты с направлений Software Engineering и Machine Learning часто идут делать НИРы в компании (в основном, JetBrains или Яндекс, но не только).

В этом посте я расскажу о своём проекте по направлению Computer Science. В рамках работы я изучил и реализовал на практике подходы к решению одной из самых известных NP-трудных задач: задаче о вершинном покрытии.

Сейчас очень быстро развивается интересный подход к NP-трудным задачам — параметризованные алгоритмы. Я постараюсь ввести вас в курс дела, рассказать несколько простых параметризованных алгоритмов и описать один мощный метод, который очень мне помог. Свой результаты я представил на соревновании PACE Challenge: по итогам открытых тестов мое решение занимает третье место, а окончательные результаты будут известны 1 июля.

О себе

Меня зовут Василий Алфёров, я сейчас заканчиваю третий курс НИУ ВШЭ — Санкт-Петербург. Алгоритмами я увлекаюсь ещё со школьных времён, когда учился в московской 179 школе и успешно участвовал в олимпиадах по информатике.

Конечное количество специалистов по параметризованным алгоритмам заходят в бар...

Пример взят из книги «Parameterized algorithms»

Представьте, что вы — охранник бара в небольшом городе. Каждую пятницу половина города приходит в ваш бар расслабиться, что доставляет вам немало хлопот: нужно выкидывать из бара буйных посетителей, чтобы не допустить драк. В конце концов, вам это надоедает и вы решаете принять превентивные меры.

Так как город у вас маленький, вы точно знаете, какие пары посетителей с большой вероятностью передерутся, если попадут в бар вместе. У вас есть список из n человек, которые придут сегодня вечером в бар. Вы решаете не пустить в бар каких-нибудь горожан таким образом, чтобы никто не подрался. В то же время ваше начальство не хочет терять прибыль и будет недовольно, если вы не пустите в бар больше чем k человек.

К сожалению, задача, стоящая перед вами — классическая NP-трудная задача. Вы могли знать её как Vertex Cover, или как задачу о вершинном покрытии. Для таких задач в общем случае неизвестны алгоритмы, работающие за приемлемое время. Если быть точным, то недоказанная и довольно сильная гипотеза ETH (Exponential Time Hypothesis) говорит, что эта задача не решается за время $$, то есть что заметно лучше полного перебора ничего нельзя придумать. Например, пусть к вам в бар собирается прийти n = 1000 человек. Тогда полный перебор составит $$ вариантов, что есть примерно $$ — безумно много. К счастью, ваше руководство поставило вам ограничение k = 10, так что количество комбинаций, которые вам нужно перебрать, гораздо меньше: количество подмножеств из десяти элементов равно $$. Это уже лучше, но всё равно не досчитается за день даже на мощном кластере.

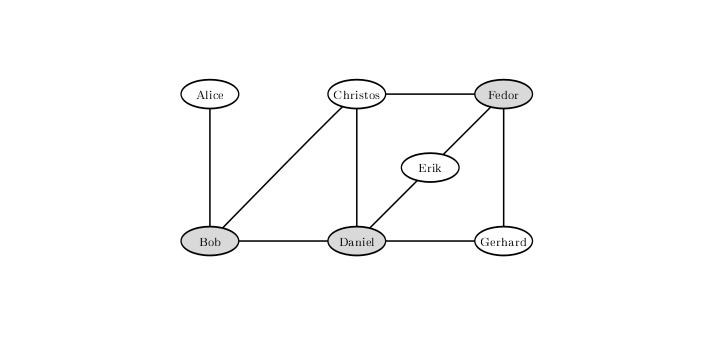
Чтобы исключить вероятность драки при такой конфигурации натянутых отношений между посетителями бара, нужно не впускать Боба, Дэниела и Фёдора. Решения, при котором за бортом останутся всего двое, не существует.

Значит ли это, что пора сдаться и впустить всех? Рассмотрим другие варианты. Ну, например, можно не впустить только тех, кто вероятно подерется с очень большим количеством народу. Если кто-то может подраться хотя бы с k + 1 другим человеком, то его точно пускать нельзя — иначе придётся не пустить всех k + 1 горожан, с кем он может подраться, что уже точно расстроит руководство.

Пусть вы выкинули всех, кого могли, по этому принципу. Тогда все остальные могут подраться не более чем с k людьми. Выкинув из них k человек, вы можете предотвратить не более чем $$ конфликтов. Значит, если всего больше чем $$ человек участвует хотя бы в одном конфликте, то вы точно не сможете предотвратить их все. Так как, понятное дело, совсем неконфликтных людей вы обязательно пустите, то вам нужно перебрать все подмножества размером десять из двухсот людей. Их примерно $$, а такое количество операций уже можно перебрать на кластере.

Если можно безопасно взять совсем не конфликтных личностей, то что про тех, кто участвует лишь в одном конфликте? На самом деле, их тоже можно впустить, закрыв двери перед их оппонентом. И правда, если Алиса конфликтует только с Бобом, то если мы впустим из них двоих Алису, мы не проиграем: у Боба могут быть другие конфликты, а у Алисы их точно нет. Тем более нам бессмысленно не пускать обоих. После таких операций остаётся не более $$ гостей с нерешённной судьбой: всего у нас $$ конфликтов, в каждом двое участников и каждый участвует хотя бы в двух. Значит, остаётся перебрать всего лишь $$ вариантов, что вполне может посчитаться за полдня на ноутбуке.

На самом деле, простыми рассуждениями можно добиться еще более привлекательных условий. Заметим, что нам обязательно нужно решить все споры, то есть из каждой конфликтующей пары выбрать хотя бы одного человека, которого мы не впустим. Рассмотрим такой алгоритм: возьмём любой конфликт, из которого удалим одного участника и рекурсивно запустимся от остатка, потом удалим другого и тоже рекурсивно запустимся. Поскольку мы на каждом шаге кого-то выкидываем, дерево рекурсии такого алгоритма — бинарное дерево глубины k, поэтому суммарно алгоритм работает за $$, где n — количество вершин, а m — количество ребер. На нашем примере это порядка десяти миллионов, что за доли секунды посчитается не только на ноутбуке, но даже на мобильном телефоне.

Приведённый выше пример — это пример параметризованного алгоритма. Параметризованные алгоритмы — это алгоритмы, которые работают за время f(k) poly(n), где p — полином, f — произвольная вычислимая функция, а k — какой-то параметр, который, вполне возможно, будет много меньше размера задачи.

Все рассуждения до этого алгоритма приводят пример кернелизации — одной из общих техник для создания параметризованных алгоритмов. Кернелизация — это уменьшение размера задачи до значения, ограниченного функцией от параметра. Полученную задачу часто называют ядром. Так, простыми рассуждениями про степени вершин мы получили квадратичное ядро для задачи Vertex Cover, параметризованной размером ответа. Существуют и другие параметры, которые можно выбрать для этой задачи (например, Vertex Cover Above LP), но мы будем обсуждать именно такой параметр.

Pace Challenge

Соревнование PACE Challenge (The Parameterized Algorithms and Computational Experiments Challenge) зародилось в 2015 году, чтобы установить связь между параметризованными алгоритмами и подходами, используемыми на практике для решения вычислительных задач. Первые три соревнования были посвящены поиску древесной ширины графа (Treewidth), поиску дерева Штейнера (Steiner Tree) и поиску множества вершин, разрезающего циклы (Feedback Vertex Set). В этом году одной из задач, в которых можно было попробовать свои силы, была описанная выше задача о вершинном покрытии.

Соревнование с каждым годом набирает популярность. Если верить предварительным данным, то в этом году только в соревновании по решению задачи вершинного покрытия приняло участие 24 команды. Стоит отметить, что соревнование длится не несколько часов и даже не неделю, а несколько месяцев. У команд есть возможность изучить литературу, придумать свою оригинальную идею и попытаться ее реализовать. По сути, данное соревнование представляет из себя исследовательскую работу. Идеи самых эффективных решений и награждение победителей пройдет совместно с конференцией IPEC (International Symposium on Parameterized and Exact Computation) в рамках самого большого ежегодного алгоритмического собрания в Европе ALGO. Более подробную информацию про само соревнование можно найти на сайте, а результаты прошлых лет лежат тут.

Схема решения

Чтобы справиться с задачей о вершинном покрытии, я попробовал применить параметризованные алгоритмы. Они, как правило, состоят из двух частей: правил упрощения (которые в идеале приводят к кернелизации) и правил расщепления. Правила упрощения — это предобработка входа за полиномиальное время. Цель применения таких правил — сведение задачи к эквивалентной задаче меньшего размера. Правила упрощения — это наиболее затратная часть алгоритма, и применение именно этой части ведет к общему времени работы $$ вместо простого полиномиального времени. В нашем случае правила расщепления основаны на том, что для каждой вершины нужно взять в ответ либо её, либо её соседа.

Общая схема такая: применяем правила упрощения, потом выбираем какую-то вершину, и делаем два рекурсивных вызова: в первом мы берём её в ответ, а в другом мы берём всех её соседей. Это мы называем расщепиться (бранчиться) по этой вершине.

В эту схему будет внесено ровно одно дополнение в следующем параграфе.

Идеи для правил расщепления (бранчинга)

Давайте обсудим, как выбрать вершину, по которой будет происходить расщепление.
Основная идея очень жадная в алгоритмическом смысле: давайте возьмём вершину максимальной степени и расщепимся именно по ней. Почему кажется, что так лучше? Потому что во второй ветке рекурсивного вызова мы таким образом уберём очень много вершин. Можно рассчитывать, что останется маленький граф и на нём мы отработаем быстро.

Этот подход с уже обсуждёнными простыми техниками кернелизации показывает себя неплохо, решает какие-то тесты размером в несколько тысяч вершин. Но, например, плохо работает для кубических графов (то есть графов, степень каждой вершины которых равна трём).
Есть ещё одна идея, основанная на достаточно простой мысли: если граф несвязный, задачу на его компонентах связности можно решать независимо, объединив ответы в конце. Это, кстати, и есть небольшая обещанная модификация в схеме, которая существенно ускорит решение: раньше в таком случае мы работали за произведение времён подсчёта ответов компонент, а теперь работаем за сумму. А для ускорения бранчинга нужно превратить связный граф в несвязный.

Как это сделать? Если в графе есть точка сочленения, нужно побранчиться именно по ней. Точка сочленения — это такая вершина, при удалении которой граф теряет связность. Найти в графе все точки сочленения можно классическим алгоритмом за линейное время. Такой подход заметно ускоряет бранчинг.

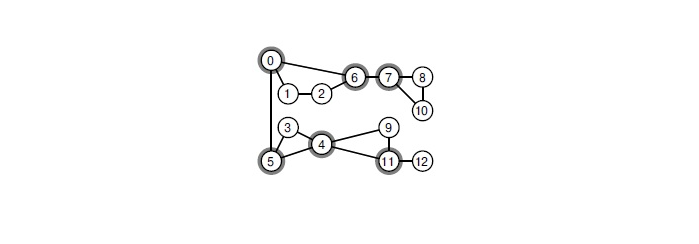
При удалении любой из выделенных вершин граф распадётся на компоненты связности.

Это мы сделаем, но хочется большего. Например, искать в графе небольшие вершинные разрезы и проводить расщепление по вершинам из него. Самый эффективный известный мне способ найти минимальный глобальный вершинный разрез — воспользоваться деревом Гомори-Ху, которое строится за кубическое время. В PACE Challenge типичный размер графа — несколько тысяч вершин. При таком раскладе в каждой вершине дерева рекурсии нужно выполнить миллиарды операций. Получается, что решить задачу за отведенное время просто невозможно.

Попробуем оптимизировать решение. Минимальный вершинный разрез между парой вершин можно найти любым алгоритмом, строящим максимальный поток. Можно напустить на такую сеть алгоритм Диница, на практике он работает очень быстро. У меня есть подозрение, что теоретически можно доказать оценку на время работы $$, что уже вполне приемлемо.

Я пробовал несколько раз искать разрезы между парами случайных вершин и брать из них самый сбалансированный. К сожалению, на открытых тестах PACE Challenge это дало плохие результаты. Я сравнивал с алгоритмом, щепившимся по вершинам максимальной степени, запуская их с ограничением на глубину спуска. После алгоритма, пытающегося найти разрез таким образом, оставались графы большего размера. Это связано с тем, что разрезы получались очень несбаллансированными: удалив 5-10 вершин, удавалось отщеплять всего лишь 15-20.

Стоит заметить, что в статьях про теоретически самые быстрые алгоритмы используются гораздо более продвинутые техники выбора вершин для расщепления. Такие техники имеют очень сложную реализацию и зачастую плохие оценки по времени и памяти. Мне не удалось выделить из них вполне приемлемые для практики.

Как применять правила упрощения

У нас уже есть идеи кернелизации. Напомню:

1. Если есть изолированная вершина, удалить её.
2. Если есть вершина степени 1, удалить её и взять её соседа в ответ.
3. Если есть вершина степени хотя бы k + 1, взять её в ответ.

С первыми двумя всё понятно, с третьей есть одна хитрость. Если в шуточной задаче про бар нам было дано ограничение сверху на k, то в PACE Challenge надо просто найти вершинное покрытие минимального размера. Это типичное преобразование задач поиска (Search Problem) в задачи решения (Decision Problem), часто между двумя видами задач не делают разницы. На практике, если мы пишем решатель задачи о вершинном покрытии, разница может быть. Например, как в третьем пункте.

С точки зрения реализации, можно поступить двумя способами. Первый подход называется Iterative Deepening. Он состоит в следующем: мы можем начать с какого-то разумного ограничения снизу на ответ, и дальше запускать наш алгоритм, используя это ограничение как ограничение на ответ сверху, не спускаясь в рекурсии ниже, чем на это ограничение. Если мы нашли какой-то ответ, он гарантированно оптимальный, иначе же можно увеличить это ограничение на единичку и снова запуститься.

Другой подход — хранить какой-то текущий оптимальный ответ и искать ответ меньшего размера, при нахождении изменяя этот параметр k для большего отсечения лишних веток в поиске.

Проведя несколько ночных экспериментов, я остановился на комбинации этих двух способов: сначала я запускаю свой алгоритм с каким-то ограничением на глубину поиска (подбирая её так, чтобы это заняло ничтожное время по сравнению с основным решением) и использую лучшее найденное решение как ограничение сверху на ответ — то есть на то самое k.

Вершины степени 2

С вершинами степени 0 и 1 мы разобрались. Оказывается, что так можно сделать и с вершинами степени 2, но для этого от графа потребуются более сложные операции.

Чтобы это объяснить, надо как-то обозначить вершины. Назовём вершину степени 2 вершиной v, а её соседей — вершинами x и y. Дальше у нас будет два случая.

1. Когда x и y — соседи. Тогда можно взять в ответ x и y, а v удалить. И правда, из этого треугольника хотя бы две вершины нужно взять в ответ и мы точно не проиграем, если возьмём x и y: у них, вероятно, есть ещё соседи, а у v их нет.
2. Когда x и y — не соседи. Тогда утверждается, что все три вершины можно склеить в одну. Идея в том, что в таком случае есть оптимальный ответ, в который мы возьмём либо v, либо обе вершины x и y. Причём в первом случае нам придётся взять в ответ всех соседей x и y, а во втором не обязательно. Это в точности соответствует случаям, когда мы не берём склеенную вершину в ответ и когда берём. Осталось лишь заметить, что в обоих случаях ответ от такой операции уменьшается на единицу.

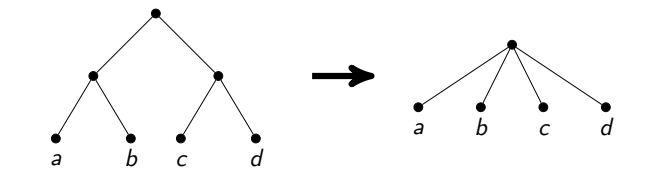
Стоит заметить, что такой подход за честное линейное время довольно сложно аккуратно реализовать. Склейка вершин — сложная операция, нужно скопировать списки соседей. Если это сделать неаккуратно, можно получить асимптотически неоптимальное время работы (например, если после каждой склейки копировать много рёбер). Я остановился на поиске целых путей из вершин степени 2 и разборе кучи частных случаев, вроде циклов из таких вершин или из всех таких вершин кроме одной.

Кроме того, нужно чтобы эта операция была обратимой, чтобы во время возврата из рекурсии мы восстановили граф в исходном виде. Для обеспечения этого я не очищал списки рёбер слитых вершин, после чего я просто знал, какие рёбра нужно куда направить. Такая реализация графов также требует аккуратности, но зато обеспечивает честное линейное время. А для графов из нескольких десятков тысяч рёбер вполне влезает в кэш процессора, что даёт большие преимущества в скорости.

Линейное ядро

Наконец, самая интересная часть ядра.

Для начала вспомним, что в двудольных графах минимальное вершинное покрытие можно искать за $$. Для этого нужно воспользоваться алгоритмом Хопкрофта-Карпа для того, чтобы найти там максимальное паросочетание, а потом воспользоваться теоремой Кёнига-Эгервари.

Идея линейного ядра такова: сначала раздвоим граф, то есть вместо каждой вершины v заведём две вершины $$ и $$, а вместо каждого ребра u — v заведём два ребра $$ и $$. Полученный граф будет двудольным. Найдём в нём минимальное вершинное покрытие. Какие-то вершины исходного графа попадут туда дважды, какие-то только один раз, а какие-то — ни разу. Теорема Немхаузера-Троттера утверждает, что в таком случае можно удалить вершины, которые не попали ни разу и взять в ответ те, которые попали дважды. Более того, она говорит, что из оставшихся вершин (тех, что попали однажды) нужно взять в ответ хотя бы половину.

Только что мы научились оставлять в графе не больше чем 2k вершин. И правда, если в остатке ответ — хотя бы половина всех вершин, то всего вершин там не больше чем 2k.

Здесь мне удалось сделать небольшой шаг вперёд. Понятно, что построенное таким образом ядро зависит от того, какое именно минимальное вершинное покрытие в двудольном графе мы взяли. Хочется взять такое, чтобы количество оставшихся вершин было минимальным. Раньше это умели делать лишь за время $$. Я же придумал реализацию этого алгоритма за время $$, таким образом, это ядро можно искать на графах в сотни тысяч вершин на каждом этапе бранчинга.

Результат

Практика показывает, что моё решение хорошо работает на тестах в несколько сотен вершин и несколько тысяч рёбер. На таких тестах вполне можно ожидать, что решение найдётся за полчаса. Вероятность нахождения ответа за приемлемое время в принципе возрастает если в графе достаточно много вершин большой степени, например степени 10 и выше.

Для участия в соревновании решения нужно было отправить на optil.io. Судя по представленной там табличке, моё решение на открытых тестах занимает третье место из двадцати с большим отрывом от второго. Если быть совсем честным, то не совсем понятно, как будут оцениваться решения на самом соревновании: например, моё решение проходит меньше тестов, чем решение на четвёртом месте, но на тех, которые проходит, работает быстрее.

Результаты на закрытых тестах станут известны первого июля.