Как можно более равномерное распределение точек на сфере — невероятно важная задача в математике, науке и компьютерных системах, а наложение сетки Фибоначчи на поверхность сферы при помощи равновеликой проекции — чрезвычайно быстрый и эффективный метод аппроксимации для её решения. Я покажу, как благодаря незначительным изменениям его можно сделать ещё лучше.

Какое-то время назад этот пост появился на главной странице Hacker News. Его обсуждение можно прочитать здесь.
Задача равномерного распределения точек на сфере имеет очень долгую историю. Это одна из самых хорошо исследованных задач в математической литературе по сферической геометрии. Она имеет критическую важность во многих областях математики, физики, химии, в том числе в вычислительных методах, теории приближений, теории кодирования, кристаллографии, электростатике, компьютерной графике, морфологии вирусов и многих других.
К сожалению, за исключением нескольких особых случаев (а именно платоновых тел) невозможно идеально ровно распределить точки на сфере. Кроме того, решение задачи сильно зависит от критерия, который используется для оценки однородности. На практике используется множество критериев, в том числе:
Очень важно уяснить этот аспект: обычно не существует единственного оптимального решения этой задачи, потому что оптимальное решение, основанное на одном критерии, часто не является оптимальным распределением точек для других. Например, мы также выясним, что оптимизация упаковки необязательно создаёт оптимальную выпуклую оболочку и наоборот.
Ради краткости в этом посте мы рассмотрим только два критерия: минимальное расстояние упаковки и выпуклую оболочку/сетку Делоне (объём и площадь).
В разделе 1 мы покажем, как можно изменить каноническую сетку Фибоначчи для построения улучшенного распределения упаковки. В разделе 2 мы покажем, как можно изменить каноническую сетку Фибоначчи для построения улучшенных параметров выпуклых оболочек (объёма и площади поверхности).
Часто эту задачу называют задачей Тэммса в честь ботаника Тэммса, искавшего объяснение структуры поверхности пыльцевых зёрен. Критерий упаковки требует от нас максимизировать наименьшее расстояние между соседями для точек. То есть
Это значение уменьшается со скоростью , поэтому полезно будет определить нормализованное расстояние, а также асимптотический предел нормализованного расстояния как
Сетка Фибоначчи
Одно очень элегантное решение моделирует узлы, встречающиеся в природе, например, распределение семян в подсолнухе или сосновой шишке. Это явление называется спиральным филлотаксисом. Коксетер показал, что такие структуры имеют фундаментальную связь с рядом Фибоначчи, и золотым сечением .
В литературе встречается два схожих определения множества точек сферической сетки Фибоначчи. Исходное определено строго для , равного одному из членов ряда Фибоначчи, , и хорошо изучено в теории чисел.
Второе определение обобщает формулу до произвольного количества и используется в вычислениях чаще:
где
Ниже показан пример таки сеток Фибоначчи. Преобразованием можно превратить эти множества точек в хорошо известные нам спирали Фибоначчи

Аналогичным образом эти множества точек можно перенести из единичного квадрата на сферу при помощи цилиндрической равновеликой проекции:
Множество различный версий код на Python для неё можно найти на stackoverflow: Evenly distributing points on a sphere.
Даже несмотря на то, что сферические множества Фибоначчи глобально не являются наилучшим распределением сэмплов на сфере (потому что их решения не совпадают с решениями для платоновых тел при ), они обладают превосходными свойствами сэмплирования и очень легки в построении по сравнению с другими, более сложными схемами сферического сэмплирования.
Так как перенос из единичного квадрата на поверхность сферы выполняется проекцией с сохранением площади, можно ожидать, что если исходные точки распределены равномерно, то они также будут достаточно хорошо распределены и на поверхности сферы. Однако это не означает, что распределение будет доказуемо оптимальным.
Такой перенос страдает от двух различных, но взаимосвязанных проблем.
Во-первых, это наложение выполняется с сохранением площади, а не расстояния. Учитывая то, что в нашем случае условием является максимизация минимального попарного расстояния между точками, то такие условия и взаимосвязи необязательно будут выполняться после проецирования.
Вторую проблему сложнее всего решить с точки зрения практики: наложение имеет на каждом полюсе две вырожденные точки. Рассмотрим две точки, находящиеся очень близко к полюсу, но отличающиеся на 180 градусов по долготе. На единичном квадрате (и на цилиндрической проекции) они будут соответствовать двум очень далёким друг от друга точкам, однако при наложении на поверхность сферы они могут быть соединены очень малой дугой, проходящей через северный полюс. Из-за этой конкретной проблемы многие спиральные наложения оказываются недостаточно оптимальными.
Сферическая спираль Фибоначчи, полученная из уравнения 1, даёт значение для всех , то есть .
Сетка 1
Более распространённая версия (особенно в компьютерных системах), создающая более хорошее значение , имеет вид:
Она располагает точки в средних точках интервалах (по правилу средней точки в квадратной формуле Гаусса), поэтому для , значения первой координаты будут такими:
Сетка 2.
Ключевым моментом для дальнейшего улучшения уравнения 2, является осознание того, что всегда соответствует расстоянию между точками и , которые находятся на полюсах. То есть для улучшения точки рядом с полюсами должны быть разнесены ещё дальше.
Если мы определим следующее распределение:
— кривые для различных значений. (синяя); (оранжевая); (зелёная); и (красная). Можно увидеть, что даёт результаты ближе к асимптотическим результатам. То есть при следующее простое выражение генерирует значительно более хорошие результаты по сравнению с канонической сферической сеткой Фибоначчи:
То есть при значения первой координаты будут равны:
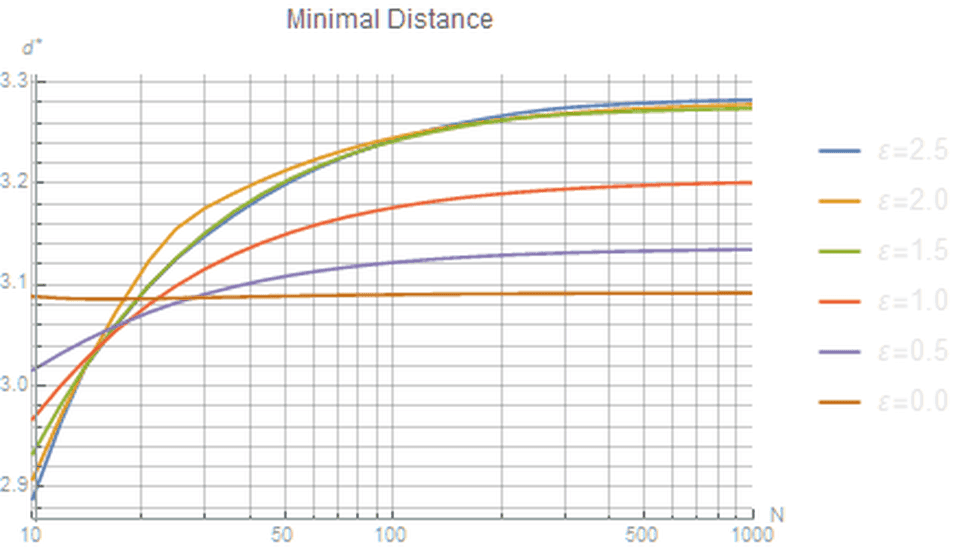
Рисунок 1. Различные значения при разных значениях . Чем больше значение, тем оптимальнее конфигурации. Мы видим, что обеспечивает решение, близкое к оптимальному.
Сетка 3.
Как сказано выше, одна из самых серьёзных проблем равномерного распределения точек на сфере заключается в том, что оптимальность распределения критически зависит от используемой целевой функции. Оказывается. что локальные величины наподобие иногда почти «не прощают ошибок» — единственная точка в недостаточно оптимальной позиции может катастрофически снизить оценку всего распределения точек.
В нашем случае вне зависимости от величины значение обычно определяется четырьмя точками, наиболее близкими к каждому из полюсов, особенно и . Однако об этой сетке также известно то, что наибольший многоугольник Вороного находится на полюсе. Таким образом, пытаясь максимизировать разделением изначальных полярных точек в ряду, мы на самом деле ещё больше увеличиваем пустоту на полюсе! Поэтому мы представили альтернативу сетке 2, которая в общем случае более предпочтительна, потому что она не демонстрирует такой большой пустоты рядом с полюсами.
Она почти идентична сетке 2, но имеет два отличия. Во-первых, она использует при . Во-вторых, кроме этих точек первая и последняя точки располагаются на каждом из полюсов.
То есть:
Удивительное свойство этого метода построения заключается в том, что несмотря на то, что его создание было мотивировано желанием минимизировать пустоты на полюсах, он на самом деле имеет наилучшее среди всех методов значение и с !
То есть при значения первой координаты будут такими:
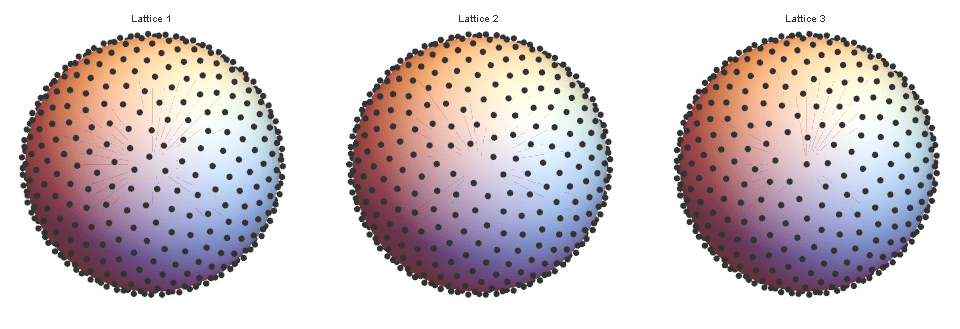
Рисунок 2. Различные конфигурации сеток. Каноническая сетка Фибоначчи слева. Заметьте, что несмотря на то, что у средней сетки улучшено, на полюсе у неё есть заметная пустота. Сетка 3 не имеет пустоты на полюсе и обладает наилучшим значением .
Сравнение
При больших значениях это значение чрезвычайно хорошо сравнимо с другими методами, например, геодезическими куполами, которые основаны на триангулированных проекциях с граней платоновых тел на поверхность сферы. Неудивительно что самые качественные геодезические купола построены на основе икосаэдра или додекаэдра.
Основанные на икосаэдре геодезические купола при различных значениях .
Основанные на додекаэдре геодезические купола при различных значениях .
Кроме того, усечённый икосаэдр, соответствующий форме фуллерена , имеет всего лишь .
То есть при сетки на основе уравнения 3 лучше любых геодезических многограннико.
По данным из первого источника в представленном ниже списке справочной литературы, некоторые из современных методов, которые обычно сложны и требуют рекурсивного и/или динамического программирования, имеют следующие показатели.
Вывод из раздела 1
В предыдущем разделе мы оптимизировали распределение по , однако эти модификации ухудшают другие показатели, например объём выпуклой оболочки (сетки Делоне). В этом разделе рассказывается, как равномерно распределить точки на сфере таким образом чтобы оптимизировать (максимизировать) такой более глобальный показатель, как объём выпуклой оболочки.
Обозначим как выпуклую оболочку точек,
сюда включён фактор нормализации , потому что абсолютное расхождение снижается со скоростью .
Поведение при различных можно увидеть на рисунке 3 (синяя линия).
Для снижения рассогласованности объёмов необходимо заметить, что несмотря на использование , из логичности золотого сечения при необязательно следует, что оно является наилучшим значением для конечного . Говоря по-научному, можно сказать, что нужно учесть влияние коррекции конечности членов.
Давайте обобщим уравнение 1 следующим образом:
где определим как
где
где — функция округления до ближайшего целого в меньшую сторону.
На рисунке 3 показано, насколько значительно оптимизируется рассогласованность объёмов для половины значений .
Причина этого заключается в малоизвестном факте: все числа , удовлетворяющие особому преобразованию Мёбиуса, исходя из иррациональности эквивалентны .
Следовательно, причина того, что и так хорошо подходят друг другу, заключается в том, что
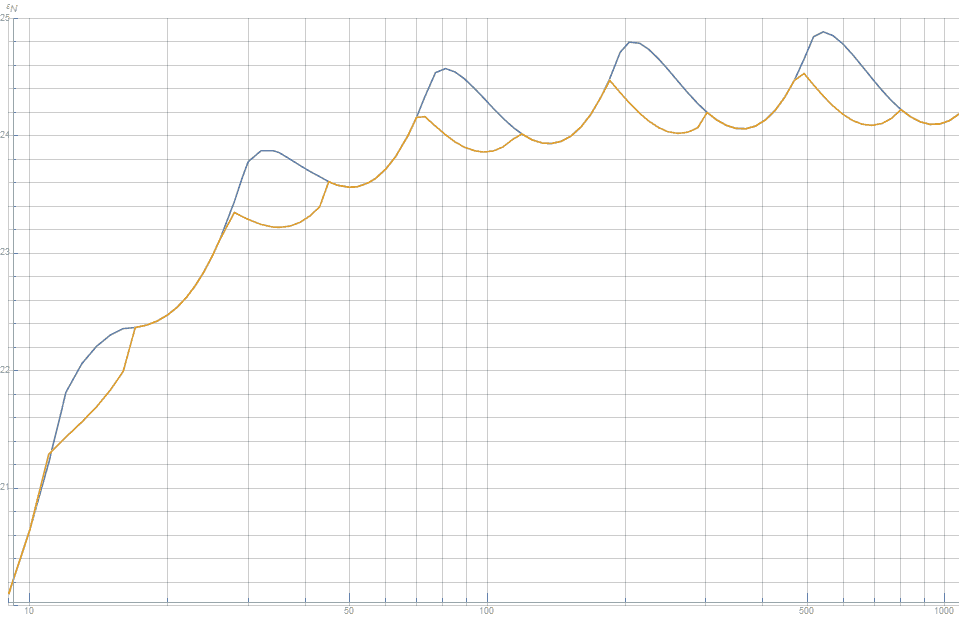
Рисунок 3. Рассогласованность между объёмом выпуклой оболочки из точек и объёмом единичной сферы. Учтите, что чем она меньше, тем лучше. Рисунок показывает, что гибридная модель (оранжевая линия), основанная на и , обеспечивает более качественное распределение точек, чем каноническая сетка Фибоначчи (голубая линия).
Для оставшейся половины мы сначала определим вспомогательный ряд , являющийся разновидностью ряда Фибоначчи
То есть
Все дроби этого ряда имеют изящные непрерывные дроби, а в пределе сходятся к . Например,
Теперь мы можем полностью обобщить следующим образом:
В таблице ниже показаны значения для различных .
Из рисунка 4 видно, что относительно объёма выпуклой оболочки это новое распределение лучше, чем каноническая сетка для всех значений
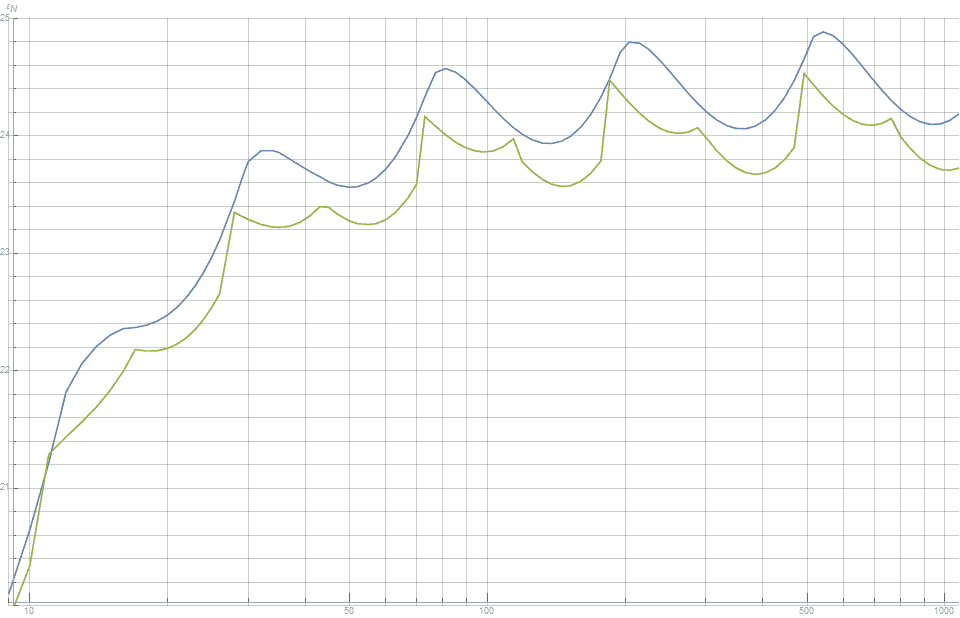
Рисунок 4. Рассогласование между объёмом выпуклой оболочки и объёмом единичной сферы. Чем меньше значения, тем лучше. Это говорит нам, что предлагаемый новый метод (зелёная линия) постоянно обеспечивает лучшее по сравнению с канонической сеткой Фибоначчи (синяя линия) распределение.
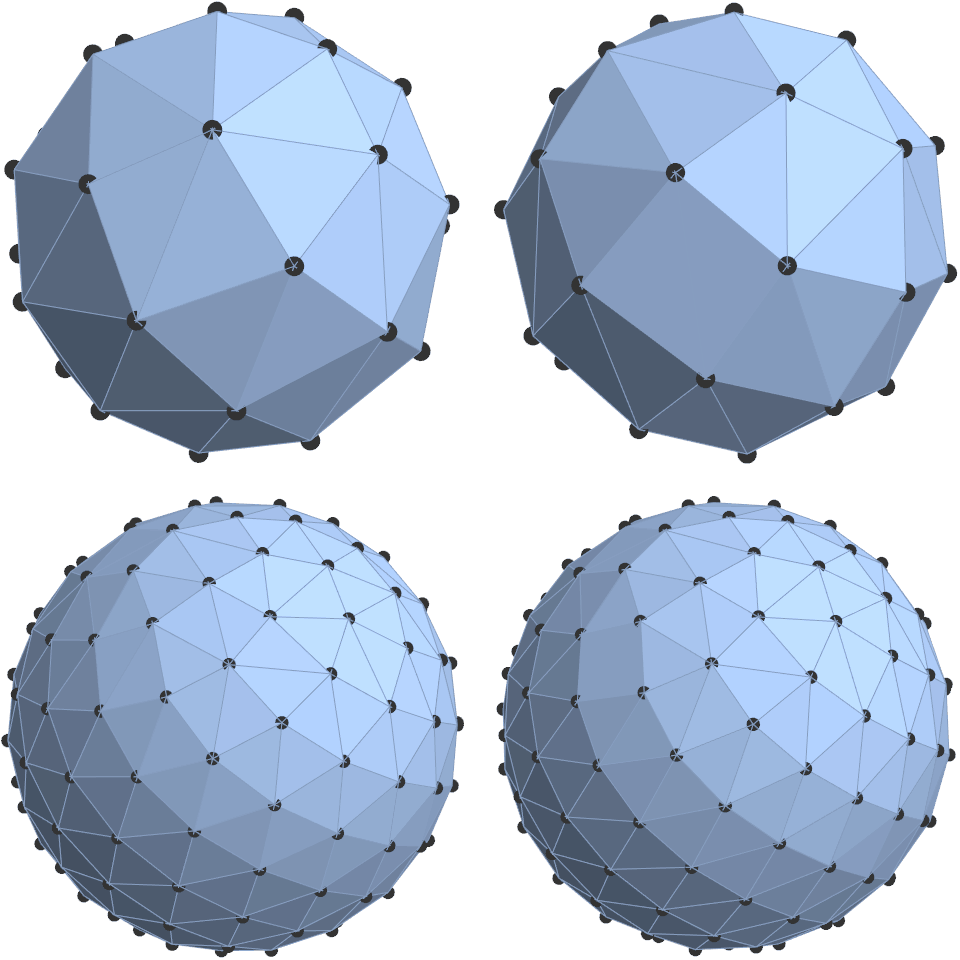
Рисунок 5. Наглядное сравнение канонической сетки (слева) с новой модифицированной сеткой (справа) при n=35 и n=150. Визуально различия почти незаметны. Однако в условиях, требующих максимальной эффективности, модифицированная версия (справа) обеспечивает небольшое, но поддающееся количественному измерению улучшению и в объёме, и в площади поверхности выпуклой оболочки.
Любопытно, что это распределение также незначительно, но неуклонно снижает рассогласование между площадью поверхности выпуклой оболочки и площадью поверхности единичной сферы. Это показано на рисунке 6.
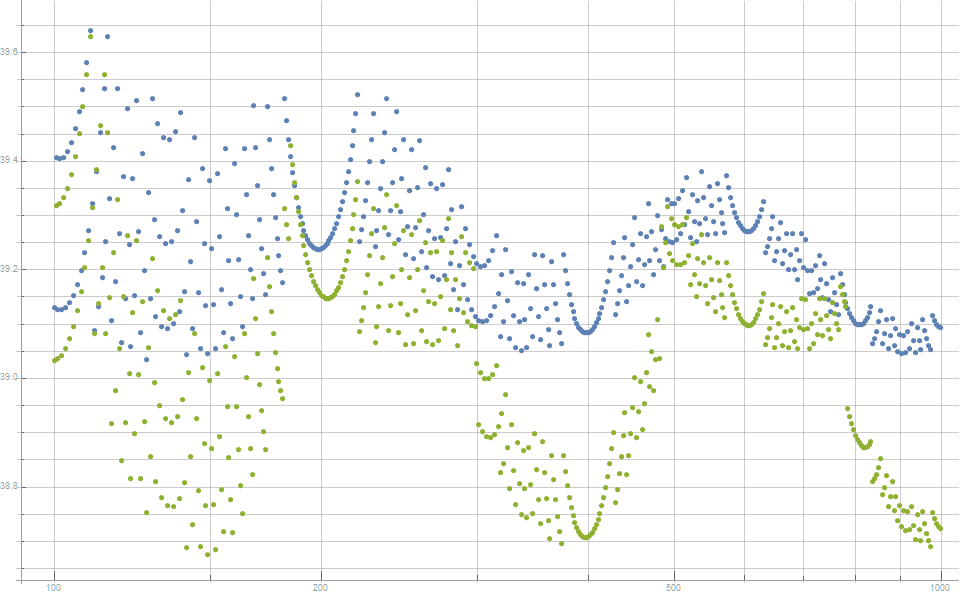
Рисунок 5. Нормализованное рассогласование площадей между площадью поверхности выпуклой оболочки (сетки Делоне) и площадью поверхности единичной сферы. Чем ниже значения, тем лучше. Это показывает, что предложенная новая модификация (зелёные точки) демонстрирует небольшое, но постоянное снижение разности площадей поверхностей по сравнению с канонической сеткой Фибоначчи (синие точки)
Вывод из раздела 2
Источники

Какое-то время назад этот пост появился на главной странице Hacker News. Его обсуждение можно прочитать здесь.
Введение
Задача равномерного распределения точек на сфере имеет очень долгую историю. Это одна из самых хорошо исследованных задач в математической литературе по сферической геометрии. Она имеет критическую важность во многих областях математики, физики, химии, в том числе в вычислительных методах, теории приближений, теории кодирования, кристаллографии, электростатике, компьютерной графике, морфологии вирусов и многих других.
К сожалению, за исключением нескольких особых случаев (а именно платоновых тел) невозможно идеально ровно распределить точки на сфере. Кроме того, решение задачи сильно зависит от критерия, который используется для оценки однородности. На практике используется множество критериев, в том числе:
- Упаковка и покрытие
- Выпуклые оболочки, ячейки Вороного и треугольники Делоне
- Ядра -энергии Риса
- Кубатура и определители
Очень важно уяснить этот аспект: обычно не существует единственного оптимального решения этой задачи, потому что оптимальное решение, основанное на одном критерии, часто не является оптимальным распределением точек для других. Например, мы также выясним, что оптимизация упаковки необязательно создаёт оптимальную выпуклую оболочку и наоборот.
Ради краткости в этом посте мы рассмотрим только два критерия: минимальное расстояние упаковки и выпуклую оболочку/сетку Делоне (объём и площадь).
В разделе 1 мы покажем, как можно изменить каноническую сетку Фибоначчи для построения улучшенного распределения упаковки. В разделе 2 мы покажем, как можно изменить каноническую сетку Фибоначчи для построения улучшенных параметров выпуклых оболочек (объёма и площади поверхности).
Раздел 1. Оптимизация расстояния упаковки
Часто эту задачу называют задачей Тэммса в честь ботаника Тэммса, искавшего объяснение структуры поверхности пыльцевых зёрен. Критерий упаковки требует от нас максимизировать наименьшее расстояние между соседями для точек. То есть
Это значение уменьшается со скоростью , поэтому полезно будет определить нормализованное расстояние, а также асимптотический предел нормализованного расстояния как
Сетка Фибоначчи
Одно очень элегантное решение моделирует узлы, встречающиеся в природе, например, распределение семян в подсолнухе или сосновой шишке. Это явление называется спиральным филлотаксисом. Коксетер показал, что такие структуры имеют фундаментальную связь с рядом Фибоначчи, и золотым сечением .
В литературе встречается два схожих определения множества точек сферической сетки Фибоначчи. Исходное определено строго для , равного одному из членов ряда Фибоначчи, , и хорошо изучено в теории чисел.
Второе определение обобщает формулу до произвольного количества и используется в вычислениях чаще:
где
Ниже показан пример таки сеток Фибоначчи. Преобразованием можно превратить эти множества точек в хорошо известные нам спирали Фибоначчи

Аналогичным образом эти множества точек можно перенести из единичного квадрата на сферу при помощи цилиндрической равновеликой проекции:
Множество различный версий код на Python для неё можно найти на stackoverflow: Evenly distributing points on a sphere.
Даже несмотря на то, что сферические множества Фибоначчи глобально не являются наилучшим распределением сэмплов на сфере (потому что их решения не совпадают с решениями для платоновых тел при ), они обладают превосходными свойствами сэмплирования и очень легки в построении по сравнению с другими, более сложными схемами сферического сэмплирования.
Так как перенос из единичного квадрата на поверхность сферы выполняется проекцией с сохранением площади, можно ожидать, что если исходные точки распределены равномерно, то они также будут достаточно хорошо распределены и на поверхности сферы. Однако это не означает, что распределение будет доказуемо оптимальным.
Такой перенос страдает от двух различных, но взаимосвязанных проблем.
Во-первых, это наложение выполняется с сохранением площади, а не расстояния. Учитывая то, что в нашем случае условием является максимизация минимального попарного расстояния между точками, то такие условия и взаимосвязи необязательно будут выполняться после проецирования.
Вторую проблему сложнее всего решить с точки зрения практики: наложение имеет на каждом полюсе две вырожденные точки. Рассмотрим две точки, находящиеся очень близко к полюсу, но отличающиеся на 180 градусов по долготе. На единичном квадрате (и на цилиндрической проекции) они будут соответствовать двум очень далёким друг от друга точкам, однако при наложении на поверхность сферы они могут быть соединены очень малой дугой, проходящей через северный полюс. Из-за этой конкретной проблемы многие спиральные наложения оказываются недостаточно оптимальными.
Сферическая спираль Фибоначчи, полученная из уравнения 1, даёт значение для всех , то есть .
Сетка 1
Более распространённая версия (особенно в компьютерных системах), создающая более хорошее значение , имеет вид:
Она располагает точки в средних точках интервалах (по правилу средней точки в квадратной формуле Гаусса), поэтому для , значения первой координаты будут такими:
Сетка 2.
Ключевым моментом для дальнейшего улучшения уравнения 2, является осознание того, что всегда соответствует расстоянию между точками и , которые находятся на полюсах. То есть для улучшения точки рядом с полюсами должны быть разнесены ещё дальше.
Если мы определим следующее распределение:
— кривые для различных значений. (синяя); (оранжевая); (зелёная); и (красная). Можно увидеть, что даёт результаты ближе к асимптотическим результатам. То есть при следующее простое выражение генерирует значительно более хорошие результаты по сравнению с канонической сферической сеткой Фибоначчи:
То есть при значения первой координаты будут равны:

Рисунок 1. Различные значения при разных значениях . Чем больше значение, тем оптимальнее конфигурации. Мы видим, что обеспечивает решение, близкое к оптимальному.
Сетка 3.
Как сказано выше, одна из самых серьёзных проблем равномерного распределения точек на сфере заключается в том, что оптимальность распределения критически зависит от используемой целевой функции. Оказывается. что локальные величины наподобие иногда почти «не прощают ошибок» — единственная точка в недостаточно оптимальной позиции может катастрофически снизить оценку всего распределения точек.
В нашем случае вне зависимости от величины значение обычно определяется четырьмя точками, наиболее близкими к каждому из полюсов, особенно и . Однако об этой сетке также известно то, что наибольший многоугольник Вороного находится на полюсе. Таким образом, пытаясь максимизировать разделением изначальных полярных точек в ряду, мы на самом деле ещё больше увеличиваем пустоту на полюсе! Поэтому мы представили альтернативу сетке 2, которая в общем случае более предпочтительна, потому что она не демонстрирует такой большой пустоты рядом с полюсами.
Она почти идентична сетке 2, но имеет два отличия. Во-первых, она использует при . Во-вторых, кроме этих точек первая и последняя точки располагаются на каждом из полюсов.
То есть:
Удивительное свойство этого метода построения заключается в том, что несмотря на то, что его создание было мотивировано желанием минимизировать пустоты на полюсах, он на самом деле имеет наилучшее среди всех методов значение и с !
То есть при значения первой координаты будут такими:

Рисунок 2. Различные конфигурации сеток. Каноническая сетка Фибоначчи слева. Заметьте, что несмотря на то, что у средней сетки улучшено, на полюсе у неё есть заметная пустота. Сетка 3 не имеет пустоты на полюсе и обладает наилучшим значением .
Сравнение
При больших значениях это значение чрезвычайно хорошо сравнимо с другими методами, например, геодезическими куполами, которые основаны на триангулированных проекциях с граней платоновых тел на поверхность сферы. Неудивительно что самые качественные геодезические купола построены на основе икосаэдра или додекаэдра.
Основанные на икосаэдре геодезические купола при различных значениях .
Основанные на додекаэдре геодезические купола при различных значениях .
Кроме того, усечённый икосаэдр, соответствующий форме фуллерена , имеет всего лишь .
То есть при сетки на основе уравнения 3 лучше любых геодезических многограннико.
По данным из первого источника в представленном ниже списке справочной литературы, некоторые из современных методов, которые обычно сложны и требуют рекурсивного и/или динамического программирования, имеют следующие показатели.
Вывод из раздела 1
Сетка 3, созданная по уравнению 3, является модификацией канонической сетки Фибоначчи, обеспечивающей гораздо более качественную упаковку распределения точек. То есть
Раздел 2. Оптимизация выпуклой оболочки (сетки Делоне)
В предыдущем разделе мы оптимизировали распределение по , однако эти модификации ухудшают другие показатели, например объём выпуклой оболочки (сетки Делоне). В этом разделе рассказывается, как равномерно распределить точки на сфере таким образом чтобы оптимизировать (максимизировать) такой более глобальный показатель, как объём выпуклой оболочки.
Обозначим как выпуклую оболочку точек,
сюда включён фактор нормализации , потому что абсолютное расхождение снижается со скоростью .
Поведение при различных можно увидеть на рисунке 3 (синяя линия).
Для снижения рассогласованности объёмов необходимо заметить, что несмотря на использование , из логичности золотого сечения при необязательно следует, что оно является наилучшим значением для конечного . Говоря по-научному, можно сказать, что нужно учесть влияние коррекции конечности членов.
Давайте обобщим уравнение 1 следующим образом:
где определим как
где
где — функция округления до ближайшего целого в меньшую сторону.
На рисунке 3 показано, насколько значительно оптимизируется рассогласованность объёмов для половины значений .
Причина этого заключается в малоизвестном факте: все числа , удовлетворяющие особому преобразованию Мёбиуса, исходя из иррациональности эквивалентны .
Следовательно, причина того, что и так хорошо подходят друг другу, заключается в том, что

Рисунок 3. Рассогласованность между объёмом выпуклой оболочки из точек и объёмом единичной сферы. Учтите, что чем она меньше, тем лучше. Рисунок показывает, что гибридная модель (оранжевая линия), основанная на и , обеспечивает более качественное распределение точек, чем каноническая сетка Фибоначчи (голубая линия).
Для оставшейся половины мы сначала определим вспомогательный ряд , являющийся разновидностью ряда Фибоначчи
То есть
Все дроби этого ряда имеют изящные непрерывные дроби, а в пределе сходятся к . Например,
Теперь мы можем полностью обобщить следующим образом:
В таблице ниже показаны значения для различных .
Из рисунка 4 видно, что относительно объёма выпуклой оболочки это новое распределение лучше, чем каноническая сетка для всех значений

Рисунок 4. Рассогласование между объёмом выпуклой оболочки и объёмом единичной сферы. Чем меньше значения, тем лучше. Это говорит нам, что предлагаемый новый метод (зелёная линия) постоянно обеспечивает лучшее по сравнению с канонической сеткой Фибоначчи (синяя линия) распределение.

Рисунок 5. Наглядное сравнение канонической сетки (слева) с новой модифицированной сеткой (справа) при n=35 и n=150. Визуально различия почти незаметны. Однако в условиях, требующих максимальной эффективности, модифицированная версия (справа) обеспечивает небольшое, но поддающееся количественному измерению улучшению и в объёме, и в площади поверхности выпуклой оболочки.
Любопытно, что это распределение также незначительно, но неуклонно снижает рассогласование между площадью поверхности выпуклой оболочки и площадью поверхности единичной сферы. Это показано на рисунке 6.

Рисунок 5. Нормализованное рассогласование площадей между площадью поверхности выпуклой оболочки (сетки Делоне) и площадью поверхности единичной сферы. Чем ниже значения, тем лучше. Это показывает, что предложенная новая модификация (зелёные точки) демонстрирует небольшое, но постоянное снижение разности площадей поверхностей по сравнению с канонической сеткой Фибоначчи (синие точки)
Вывод из раздела 2
Сетка, соответствующая уравнению 6, является модификацией канонической сетки Фибоначчи, создающей значительно лучшее распределение точек, исходя из объёма и площади поверхности выпуклой оболочки (сетки Делоне).
Источники
- A Comparison of popular point confugrations on S^2“:
- web.archive.org/web/20120421191837
- www.cgafaq.info/wiki/Evenly_distributed_points_on_sphere
- perswww.kuleuven.be/~u0017946/publications/Papers97/art97a-Saff-Kuijlaars-MI/Saff-Kuijlaars-MathIntel97.pdf
- projecteuclid.org/download/pdf_1/euclid.em/1067634731
- maths-people.anu.edu.au/~leopardi/Leopardi-Sphere-PhD-Thesis.pdf
- www.irit.fr/~David.Vanderhaeghe/M2IGAI-CO/2016-g1/docs/spherical_fibonacci_mapping.pdf
- arxiv.org/pdf/1407.8282.pdf
- maths-people.anu.edu.au/~leopardi/Macquarie-sphere-talk.pdf


Griboks
Любопытно, разве Монте-Карло не даёт идеального распределения при больших N?
Soffort
Ага. С определённой вероятностью, зависящей от величины N :)
Phaker
С нулевой вероятностью. Каковы шансы, случайно выбирая точки на отрезке [0, 1], заполнить его строго равномерно (все расстояния между соседними парами точек равны)? Шансов нет.
Soffort
Строго математически — шансы нулевые. Но если нам «ехать», т.е. для практических целей, то можно попробовать. Хоть и не нужно, если уже есть готовые алгоритмы.
Griboks
Почему с нулевой? Мы говорим про сферу, а не отрезок. Хотите узнать вероятность? Возьмите интеграл объёма границы (толщины) сферы.
Griboks
Не заметил. Вероятность, согласно центральной предельной теореме, стремиться к 1. Ну а c вычислительной точки зрения, она равняется 1. Впрочем, я сгенерировал случайные точки, можете сами проверить.
mayorovp
Какое нафиг стремление к 1?
Посмотрите внимательнее чего именно пытаются добиться в этой статье. А пытаются добиться чтобы точки на сфере шли как можно более ровной сеткой.
Случайные же точки выглядит как-то так (взял первую попавшуюся картинку, можете попробовать нарисовать ваши точки — должно получиться что-то похожее):
Griboks
Ну давайте проверим: берём отрезок от 0 до 1 и рассыпаем на него точки.
Количество точек / Среднее / Дисперсия / Отношение дисперсии к среднему
N=10^1 Mx=0.1057107049613101 Dx=0.014991353458562295 DMRx=0.14181490383636264
N=10^2 Mx=0.009925959274512302 Dx=0.00010322180977963227 DMRx=0.010399177240700892
N=10^3 Mx=0.0009988373664351917 Dx=1.0482468240416785e-06 DMRx=0.0010494669695656532
N=10^4 Mx=9.999876742558959e-05 Dx=9.68829614329053e-09 DMRx=9.6884155602215e-05
N=10^5 Mx=1.000006934144877e-05 Dx=9.968157388129179e-11 DMRx=9.968088267960981e-06
N=10^6 Mx=1.0000006018870852e-06 Dx=9.99976735903523e-13 DMRx=9.999761340308023e-07
N=10^7 Mx=9.999998466395956e-08 Dx=9.998199637750894e-15 DMRx=9.998201171079068e-08
Кокой вывод можно сделать? Генератор случайных чисел на компьютере не идеальный + точность == порядку N + отношение Dx/Mx уменьшается с ростом количества точек и стремиться к нулю. Следовательно, при большом количестве точек погрешность занимает больше 32 бит и обнуляется. Получаем абсолютно равномерное распределение.
mayorovp
Вот только если уж говорить про и правда большие N — то разрядность тоже должна стремиться к бесконечности (в том числе разрядность ГСЧ!). Иначе вся случайность вырождается в равномерную сетку из 232 ячеек, а этот вариант никому не интересен.
Griboks
Однако количество разрядов погрешности растёт быстрее, поэтому можно ограничиться, например, 32 битами (а в общем случае условием задачи) и быть уверенными, что это равномерное распределение без дополнительных критериев. Или вы не согласны?
amphasis
Вам же объяснили, что это не то равномерное распределение которого пытаются добиться в статье. Вы говорите о равномерном распределении случайной величины. В статье говорится о минимизации разброса расстояний между соседними точками на сфере, что, предвещая ваш следующий комментарий, для краткости и удобства читателя назвали равномерным распределением точек на сфере.
Griboks
1. Я говорю о псевдонормальном распределении случайной величины расстояния между соседними точками (см. центральную предельную теорему).
2. В статье говорится о равномерном (но не статистическом; однородном, если хотите) распределении точек (см. заголовок и вступление).
3. В качестве меры равномерности предлагаются 4 критерия, 2 из которых рассматриваются на примерах.
4. Я показываю теоретически и проверяю практически, что методом Монте-Карло возможно равномерно распределить точки при большом их количестве.
Теперь, пожалуйста, объясните мне ещё раз, что вы пытались сказать, и почему этот ваш разброс расстояний между соседними точками в 9.9e-08 нельзя назвать удовлетворительным?
amphasis
А вы попробуйте посчитать не абсолютную величину разброса, а разброс относительно среднего расстояния между точками (причем не на отрезке, а хотя бы на плоскости).
Почитайте введение внимательнее, там довольно ясно описано к какому распределению стремятся.
Griboks
Хорошо, получается ~ 100%. Вы предлагаете брать не среднее расстояние, а минимальное? Ну хорошо, давайте возьмём:
N=10^1 Min=0.016212136413931155 Max=0.37461837137749365 Mean=0.09401552286663975
N=10^2 Min=1.9124122053626458e-05 Max=0.04580802524341976 Mean=0.01002876616106881
N=10^3 Min=5.292099047871091e-07 Max=0.00662962744940665 Mean=0.0010004000030152745
N=10^4 Min=3.842715812218955e-09 Max=0.0008187438221771703 Mean=0.00010000210209493355
N=10^5 Min=1.6746826148050786e-11 Max=0.00011494501323361384 Mean=9.999970245561979e-06
N=10^6 Min=6.814548925149211e-13 Max=1.3744202724041976e-05 Mean=9.999999409152049e-07
N=10^7 Min=3.4083846855992306e-14 Max=1.929901522923494e-06 Mean=1.0000000462518477e-07
Какой из этого мне надо сделать вывод?
amphasis
Griboks
А у вас есть требуемое граничное значение dN для сферы моего радиуса и моего N, чтобы так говорить? Думаю, тут дело не в относительной погрешности, а в точности. В этом ведь и есть суть центральной предельной теоремы: количество перерастает в качество.
mayorovp
Почему вы так уверены, что количество разрядов погрешности растёт быстрее?
Griboks
Посчитал. У вас получились другие результаты?
mayorovp
Вы считали численно? А у использованного ГСЧ было сколько разрядов?
Вы постулировали что 32 разряда вам хватит — максимум, и получили в результате что 32 разряда вам хватит.
Griboks
Думаю, так получилось потому, что я заранее определил точность, как в реальной задаче. А может просто так сгенерировалось.
Griboks
Еще раз проверил. Вы были правы — растёт одинаково, вырождается в сетку. Однако, мы всё-равно можем изменять масштаб это сетки, пока она не будет казаться однородной.
amphasis
Но ведь в этом случае во-первых проще сразу взять нужную сетку, во-вторых при натягивании этой сетки на сферу все равно придется бороться с неоднородностями вызванными преобразованием координат.
Griboks
1. нужную сетку нужно как-то сгенерировать
2. речь идёт об изначально сферической сетке в 3d
mayorovp
Ах да, вот еще момент. Отношение дисперсии к матожиданию ничего не означает, это величины разных порядков. Надо смотреть на отношение стандартного отклонения к матожиданию.
ialexander
Там немного другая задача. Там пытаются равномерно распределить N точек на сфере. Есть разные критерии равномерности — например, минимальное расстояние между двумя точками. Таким образом, максимизируя минимальное расстояние между точками, мы располагаем точки по узлам сетки, с равным расстоянием между соседними узлами. Это оптимальное решение.
Предлагаемый в статье подход даёт приемлемое решение для любых N, в числе малых в районе 10.
Положим Монте-Карло может для больших N разместить точки близко к узлам равномерной сетки. Но Монте-Карло работает только для (очень) больших N. Его бессмысленно использовать даже для N в районе 1000.
Griboks
Спасибо за внятный ответ. Сразу становится понятно, почему его не упомянули.
Phaker
Промахнулся, удалил.