Какой маршрут будет самым безопасным, где больше всего врагов и где ближайшая аптечка? Все эти часто встречающиеся задачи о пространственных связях можно эффективно решать при помощи математических разбиений под названием «диаграммы Вороного». Из этого поста вы узнаете, как анализировать игровые карты и получать информацию, обеспечивающую реализм и успех искусственного интеллекта.

---

Пространственные отношения

Пространственное отношение — это любая информация, описывающая, как связан один объект в пространстве с другим. Примеры: расстояние между ними, площадь покрываемого каждым из них пространства и пересечение этих площадей, количество таких объектов, расположенных в одной области.

Такие отношения постоянно используются в видеоиграх и могут предоставлять очень полезную информацию ИИ, а также самому игроку.

---

У Вороного есть ответ

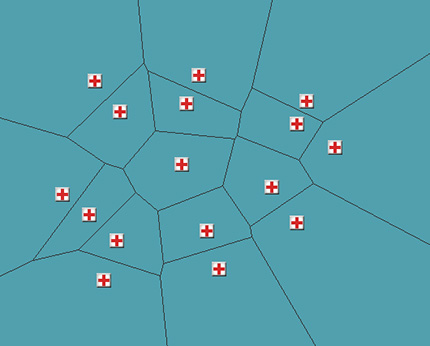
Диаграмма Вороного описывает пространственное отношение между близко расположенными точками или их их ближайшими соседями. Это множество соединённых многоугольников, полученных из точек или локаций. Каждая линия «области» Вороного находится посередине между двумя точками.

Чтобы разобраться, взглянем на картинку:


Как видите, каждая линия находится ровно посередине между двумя точками, и все они соединяются в центре. Добавим в сцену ещё несколько точек и посмотрим, что произойдёт:


Картина стала интереснее! У нас уже появляются настоящие области.

О чём же нам говорит каждая из областей? Мы знаем, что находясь в области, гарантированно расположены ближе всего к одной точке, которая тоже находится в области. Это многое говорит нам о том, что находится поблизости; таково фундаментальное пространственное отношение в диаграммах Вороного.

---

Выворачиваем Вороного наизнанку: триангуляция Делоне

Система, обратная диаграмме Вороного, называется триангуляцией Делоне. Эта диаграмма состоит из линий от каждой точки до её ближайших соседей, и каждая линия перпендикулярна пересекаемому ею ребру Вороного. Вот как это выглядит:


Белым обозначены линии Делоне. Каждая линия Делоне соответствует одному и только одному ребру Вороного. Поначалу кажется, что некоторые из них пересекают несколько рёбер, но приглядевшись, вы поймёте, что это не так.


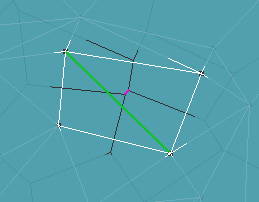
На рисунке зелёная линия Делоне соответствует розовому ребру Вороного. Просто представьте, что розовое ребро идёт дальше, и вы увидите, что они пересекаются.

Благодаря триангуляции Делоне мы видим, что вместо многоугольников у нас теперь есть множество треугольников. Это невероятно полезно, потому что мы разделили область на треугольники, которые можно рендерить. Эту методику можно применять для тесселяции или триангуляции фигур. Отлично!

Кроме того, это отличный способ создания из множества точек графа на случай, если мы захотим перемещаться от одной точки к другой. Например, точки могут обозначать города.

---

Структура данных Вороного

Мы уже знаем, как выглядит диаграмма Вороного; теперь давайте посмотрим, как будет выглядеть её структура данных. Сначала нам нужно сохранить точки, являющиеся основой диаграммы Вороного:

class VoronoiPoint {
    float x
    float y
    VoronoiRegion* region
}

Каждая VoronoiPoint имеет локацию (x, y) и ссылку на область, в которой она находится.

Далее нам нужно описать VoronoiRegion:

class VoronoiRegion {
    VoronoiPoint* point
    Edge *edges[] // our list of edges
}

Область хранит ссылку на её VoronoiPoint, а также на список ограничивающих её рёбер VoronoiEdges.

Посмотрим, как выглядит VoronoiEdges:

class VoronoiEdge {
    VoronoiPoint* pointA
    VoronoiPoint* pointB
    float distance // distance between point A and point B
    float x1, z1, x2, z2 // to visualize start & end of the edge
}

Ребро знает задающие её две точки, а также расстояние между ними. Для визуального отображения, а также для построения формы многоугольной области нам нужно хранить начальную и конечную точки ребра.

И на этом всё. Имея эту информацию, мы можем запросто построить диаграмму Вороного. Ниже мы узнаем, как диаграмма Вороного генерируется. Но пока посмотрим на паре примеров, как можно использовать эти данные.

---

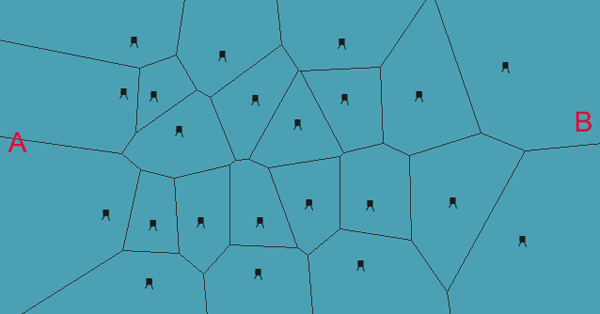
Поиск ближайшей аптечки

Снова взглянем на диаграмму Вороного для точек.


Если каждая точка обозначает аптечку, то мы довольно быстро можем определить, где находится ближайшая к нам, но сначала нужно определить область, в которой мы находимся. Диаграммы Вороного не обеспечивают эффективного способа определения области, однако для ускорения поиска мы можем хранить ссылку на каждую область в дереве квадрантов или в R-дереве. А узнав область, мы сможем узнать её соседей, и соседей её соседей.

Например, если аптечки в вашей области больше нет, то вам нужно найти путь к другой ближайшей. Из структуры данных и показанного выше псевдокода можно понять, что зная область, мы можем узнать её рёбра. А при помощи этих рёбер мы можем получить соседей. Будем брать ближайшего соседа и смотреть, есть ли в нём аптечка.

Здесь также можно применить триангуляцию Делоне. Она состоит и линий между аптечками. Тогда её можно обойти при помощи алгоритма поиска пути A*, чтобы найти ближайшую аптечку.

---

Поиск безопасного маршрута

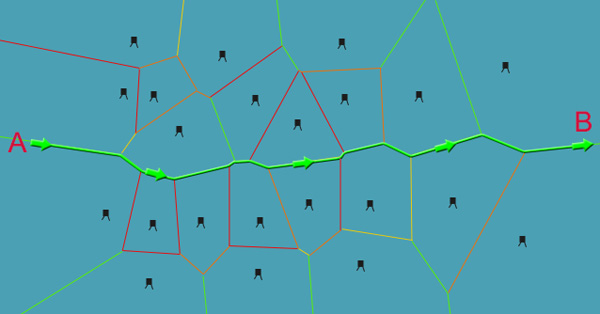
Заменим все аптечки вражескими сторожевыми вышками. Вам нужно найти самый безопасный маршрут между ними, чтобы не быть пойманным. Стандартный способ обхода графа в видеоиграх — использование алгоритма A*. Так как диаграмма Вороного — это граф, реализовать поиск очень легко. Нам всего лишь потребуется алгоритм A*, поддерживающий общие структуры графов; планируйте всё заранее, и это поможет вам в будущем.

Подготовив граф, нужно назначить каждому ребру вес. Для нас значением веса будет расстояние до этих сторожевых вышек, и получить его можно непосредственно из структуры данных: каждое VoronoiEdge уже знает своё расстояние между двумя точками. Обычно чем меньше значение на ребре A*, тем лучше, но в нашем случае лучше будет большее значение, потому что оно обозначает расстояние до башни.

Вот как выглядит начальный граф, если мы хотим переместиться из точки A в точку B:


Приложив к каждому ребру вес, мы увидим, какой маршрут лучше будет выбрать:


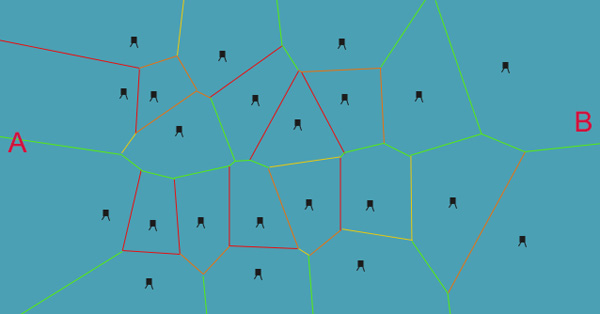
Красные рёбра обозначают ближайшие контакты с башнями. Оранжевым обозначены более дальние; жёлтым ещё более дальние, и, наконец, зелёные — самые безопасные. После выполнения A* с этими весами мы получим следующий путь:


При таком использовании весов будет выбран не самый быстрый, а самый безопасный путь, что нам и нужно. ИИ следует придерживаться этого пути и не отклоняться от него!

Можно сделать ещё один шаг, чтобы гарантировать безопасный путь: устранить все рёбра, находящиеся ближе, чем минимальное безопасное расстояние. Например, если каждая сторожевая башня имеет радиус видимости 30 единиц, то все рёбра, расстояние до точек которых меньше, можно будет удалить из графа и не обходить их.

Также можно использовать этот метод для поиска самого широкого маршрута для крупных юнитов, неспособных проходить через узкие места. У каждого ребра есть расстояние между двумя точками, поэтому мы знаем, смогут ли они пройти в этом пространстве.

Можно совершить и обратную операцию — использовать триангуляцию Делоне диаграммы, и получить линии, идущие от каждой сторожевой башни. ИИ охранников сможет быстро определять, какие другие башни находятся поблизости и при необходимости направиться к ним на помощь.

---

Поиск плотно расположенный набор предметов

Допустим, нам нужно сбросить с самолёта посылку с кошачьей мятой для кучи сидящих на земле котиков. Куда лучше всего её сбросить, чтобы ею воспользовалось наибольшее количество кошек? Это может оказаться чрезвычайно затратными расчётами. Но, к счастью, мы можем сделать обоснованное предположение при помощи триангуляции Делоне.

Подсказка: не забывайте, что триангуляция Делоне — это просто инверсия диаграммы Вороного. Она образована соединением каждой точки Вороного с соседними точкаи, полученными из списка рёбер.

Получив эту коллекцию треугольников, можно исследовать площадь, покрываемую каждым из треугольников. Если мы найдём треугольник с наименьшей площадью, тогда у нас есть три ближайшие точки, или кошки. Это может и не быть самое плотное в среднем скопление на поверхности, но станет неплохим предположением. Если бы мы могли сбрасывать несколько посылок с мятой, то просто пометили бы уже выбранные треугольники и перешли бы к следующим по увеличению размера.

Обозначение таких областей также называется описанными окружностями триангуляции Делоне. Каждая окружность — это наибольшая окружность, которая может поместиться в точках треугольника. Вот изображение описанных окружностей для диаграммы Вороного:


Можно использовать точный центр окружностей для определения центра области сброса посылки с кошачьей мятой. На самом деле радиус окружности — это более подходящий способ для определения наилучшего треугольника для сброса вместо площади треугольника, особенно если две точки треугольника очень близки друг к другу, а третья находится далеко; тогда получается очень острый треугольник с малой площадью, но определяющие его точки на самом деле очень далеко друг от друга.

---

Реализация диаграмм Вороного

Существует несколько способов генерации диаграмм Вороного, и выбор используемой методики зависит от времени, в которое мы получаем данные.

Алгоритм Форчуна

Самый быстрый способ называется алгоритмом Форчуна. Он выполняется за O(n log(n)) и требует, чтобы все точки, используемые для генерации графа, были известны на момент начала генерации. Если позже вы будете добавлять новые точки, то придётся заново генерировать весь граф. Если точек мало, то это может и не вызывать проблем, но если их у вас 100 тысяч, то это может занять много времени!

Реализация этого алгоритма нетривиальна. Необходимо пересекать параболы и учитывать особые случаи. Однако это самый быстрый метод. К счастью, существует множество реализации этого алгоритма с открытым кодом, которые можно использовать, и я привёл ссылки на них ниже.

Давайте посмотрим, как он работает.

Алгоритм заключается в скольжении линии (вертикальной или горизонтальной) по области с точками. Когда он встречает точку, то начинает рисовать из неё параболу, которая продолжается заметающей линией. Вот анимация этого процесса:


Пересекающиеся параболы образуют рёбра Вороного. Но почему параболы?

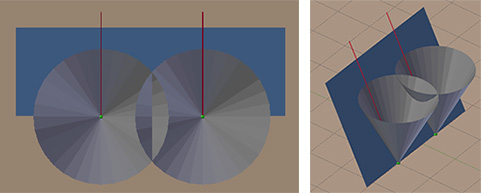
Чтобы понять это, представьте каждую точку как содержащую надувной шар, который раздувается, пока не столкнётся с другим шаром. Можно перенести эту идею на окружности, расширяющиеся на 2D-плоскости. Мы сделаем ещё один шар вперёд и разместим в каждой точке перевёрнутый конус с углом наклона 45 градусов, увеличивающийся до бесконечности. Затем представим заметающую прямую в виде линии, тоже под 45 градусов, которая скользит вдоль, пока не столкнётся с конусами. Так как плоскость и конусы расположены под одним углом, при пересечении они образуют параболы.


Увеличиваясь вверх, конусы рано или поздно пересекутся с одним или несколькими другими конусами. Если мы взглянем на места пересечения конусов, или окружностей, то получим прямые линии рёбер Вороного. На рисунке красной линией обозначено место пересечения конусов. Если конусы будут расти ещё дальше (вертикально вверх в бесконечность), то красная линия будет продолжать растягиваться.


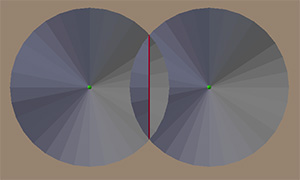
Когда плоскость скользит и происходит первый контакт с конусом, получившаяся линия будет такой:


При дальнейшем движении плоскости по конусам мы увидим, как образуются параболы:


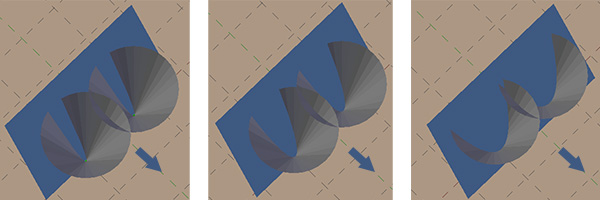
Плоскость продолжает двигаться по сцене. Для каждой встреченной точки она исследует соседние точки на заметающей линии, уже имеющие параболы и начинает новую параболу в этой точке. Она продолжает двигаться дальше и расти, пока эта новая парабола не начнёт накладываться не на ту, на которую накладывалась раньше. Затем эта предыдущая парабола закрывается. Это точка, в которой встречаются линии Вороного трёх точек.

Как сказано выше, это довольно сложно понять, поэтому вот ссылки на реализации с открытым кодом, которые можно использовать и изучать:

• Java на GitHub. Авторы: Benny Kj?r Nielsen и Allan Odgaard https://github.com/sorbits/visual-fortune-algorithm/tree/master
  
• Python на GitHub: https://github.com/MikkoJo/Voronoi. Автор: Mikko Johansson
• Подробная реализация алгоритма Форчуна: http://blog.ivank.net/fortunes-algorithm-and-implementation.html

Инкрементная вставка треугольников

Другой метод заключается в инкрементной вставке по одной точке за раз, начиная с базового треугольника из трёх точек за пределами возможной области всех других точек. Этот метод выполняется с O(n^2) и не требует наличия всех точек на момент генерации.

При вставке новой точки она определяет существующую область, в которую она попадает. Эта область затем подразделяется и создаются новые области.

Вот пример с открытым исходным кодом для использования и изучения:

• Исходник на Java. Автор: Paul Chew. Для свободного использования. Скачать ZIP-файл. Источник: http://www.cs.cornell.edu/home/chew/Delaunay.html

---

Заключение

Теперь вы должны представлять, что могут дать диаграммы Вороного вашей игре и её ИИ. При наличии правильно структурированного графа узлов и рёбер можно запрашивать важную информацию, чтобы все получили свои аптечки, кошачью мяту и пробрались мимо вражеских башен.