17.09.2019 09:30
ru_vds 41 14400 Источник
Посмотрим правде в глаза: никто не любит дробные числа — даже компьютеры.

Когда речь заходит о языке программирования COBOL — первый вопрос, который всплывает у всех в голове, всегда выглядит так: «Почему человечество всё ещё использует этот язык во множестве жизненно важных областей?». Банки всё ещё пользуются COBOL. Около 7% ВВП США зависит от COBOL в деле обработки платежей от CMS. Налоговая служба США (IRS), как всем хорошо известно, всё ещё использует COBOL. В авиации тоже используется этот язык (отсюда я узнала одну интересную вещь на эту тему: номер бронирования на авиабилетах раньше был обычным указателем). Можно сказать, что множество весьма серьёзных организаций, идёт ли речь о частном или государственном секторе, всё ещё используют COBOL.



> Вторая часть

Автор материала, первую часть перевода которого мы сегодня публикуем, собирается найти ответ на вопрос о том, почему COBOL, язык, который появился в 1959 году, всё ещё настолько распространён.

Почему COBOL всё ещё жив?


Традиционный ответ на этот вопрос глубоко циничен. Организации — это лень, некомпетентность и тупость. Они гонятся за дешевизной и не склонны к тому, чтобы вкладывать деньги в переписывание своих программных систем на чём-то современном. В целом можно предположить, что причина того, что работа столь значительного количества организаций зависит от COBOL, представляет собой комбинацию инерции и недальновидности. И в этом, конечно, есть доля истины. Переписывание больших объёмов запутанного кода — это масштабная задача. Это дорого. Это сложно. И если существующее ПО, по-видимому, работает хорошо, у организации не будет особенно сильной мотивации для инвестирования в проект по обновлению этого ПО.

Всё это так. Но когда я работала на IRS ветераны COBOL рассказывали о том, что они пытались переписать код на Java и оказалось, что Java не может правильно выполнять вычисления.

Для меня это звучало крайне странно. Настолько странно, что у меня сразу же возникла паникёрская мысль: «Господи, значит IRS округляла всем налоговые платежи в течение 50 лет!!!». Я просто не могла поверить в то, что COBOL способен обойти Java в плане математических вычислений, необходимых IRS. В конце концов — людей-то в космос они не запускали.

Один из интересных побочных эффектов того, что летом я изучала COBOL, заключается в том, что я начала понимать следующее. Дело не в том, что Java не может правильно выполнять математические вычисления. Дело в том — как именно Java делает вычисления корректными. И когда понимаешь то, как вычисления выполняются в Java, и то, как то же самое делается в COBOL — начинаешь понимать и то, почему многим организациям так сложно избавиться от своего компьютерного наследия.

Над какими «i» надо расставить точки?


Я сейчас немного отойду от рассказа о COBOL и расскажу о том, как компьютеры хранили информацию до того, как двоичное представление данных стало стандартом де-факто (а вот материал о том, как пользоваться интерфейсом z/OS; это — нечто особенное). Я так думаю, что в деле рассмотрения нашего вопроса полезно будет уклониться от основной темы в эту сторону. В вышеупомянутом материале я рассказывала о различных способах использования двоичных переключателей для хранения чисел в двоичной, троичной, десятичной системах счисления, для хранения отрицательных чисел — и так далее. Единственное, чему я не уделила достаточно внимания — это то, как хранятся десятичные числа.

Если бы вы проектировали собственный двоичный компьютер — то вы могли бы начать работу с принятия решения о том, что будете пользоваться двоичной системой счисления. Биты слева от точки представляют целые числа — 1, 2, 4, 8. А биты справа — дробные числа — 1/2, 1/4, 1/8…


2.75 в двоичном представлении

Проблема тут заключается в том, чтобы понять — как хранить саму десятичную точку (на самом деле — мне следовало бы сказать «двоичную точку» — ведь, в конце концов, говорим-то мы о двоичных числах). Это — не какая-нибудь «компьютерная алхимия», поэтому вы вполне можете догадаться о том, что я говорю о числах с плавающей точкой и о числах с фиксированной точкой. В числах с плавающей точкой двоичная точка может быть поставлена где угодно (то есть — она может «плавать»). Положение точки сохраняется в виде экспоненты. Возможность перемещать точку даёт возможность хранения более широкого диапазона чисел, чем доступно при отсутствии подобной возможности. Десятичную точку можно переместить в самую заднюю часть числа и выделить все биты для хранения целых значений, представляя очень большие числа. Точку можно сместить в переднюю часть числа и выражать очень маленькие значения. Но эта свобода даётся ценой точности. Взглянем ещё раз на двоичное представление числа 2.75 из предыдущего примера. Переход от четырёх до восьми — это гораздо больше, чем переход от одной четвёртой к одной восьмой. Возможно, нам легче будет себе это представить, если переписать пример так, как показано ниже.


Я выбрала расстояния между цифрами на глаз — просто чтобы продемонстрировать мою идею

Разницу между числами несложно вычислить самостоятельно. Например, расстояние между 1/16 и 1/32 — это 0.03125, но расстояние между 1/2 и 1/4 — это уже 0.25.

Почему это важно? В случае двоичного представления целых чисел это значения не имеет — расстояние между соседними числами двоичной записи можно легко компенсировать, заполнив их соответствующими комбинациями битов и не потеряв в точности. Но в случае с представлением дробных чисел не всё так просто. Если попытаться «заполнить» «дыры» между соседними числами — что-нибудь может «провалиться» (и на самом деле проваливается) в эти дыры. Это ведёт к тому, что в двоичном формате не удаётся получить точные представления дробных чисел.

Это иллюстрирует классический пример числа 0.1 (одна десятая). Как представить это число в двоичном формате? 2-1 — это 1/2, или 0.5. Это — слишком большое число. 1/16 — это 0.0635. Это — слишком мало. 1/16+1/32 — это уже ближе (0.09375), но 1/16+1/32+1/64 — это уже больше, чем нам нужно (0.109375).

Если вы полагаете, что эти рассуждения можно продолжать бесконечно — то вы правы — так оно и есть.

Тут вы можете сказать себе: «А почему бы нам просто не сохранить 0.1 точно так же, как мы храним число 1? Число 1 мы можем сохранить без всяких проблем — так давайте просто уберём десятичную точку и будем хранить любые числа так же, как храним целые числа».

Это — отличное решение данной проблемы за исключением того, что оно требует фиксации двоичной/десятичной точки в некоем заранее заданном месте. В противном случае числа 10.00001 и 100000.1 будут выглядеть совершенно одинаково. Но если точка зафиксирована так, что на дробную часть числа выделено, скажем, 2 знака, то мы можем округлить 10.00001 до 10.00, а 100000.1 превратится 100000.10.

Только что мы «изобрели» числа с фиксированной точкой.

С представлением разных значений с помощью чисел с фиксированной точкой мы только что разобрались. Делать это просто. Можно ли, используя числа с фиксированной точкой, облегчить решение ещё каких-нибудь задач? Вспомним тут о наших хороших друзьях — о двоично-десятичных числах (Binary Coded Decimal, BCD). Кстати, чтобы вы знали, именно эти числа используются в большинстве научных и графических калькуляторов. От этих устройств, что совершенно ясно, ждут правильных результатов вычислений.


Калькулятор TI-84 Plus

Рекуррентное соотношение Мюллера и Python


Числа с фиксированной точкой считают более точными из-за того, что «дыры» между числами постоянны, и из-за того, что округление происходит лишь тогда, когда нужно представить число, для которого просто не хватает места. Но при использовании чисел с плавающей точкой мы можем представлять очень большие и очень маленькие числа, используя один и тот же объём памяти. Правда, с их помощью нельзя представить все числа в доступном диапазоне точно и мы вынуждены прибегать к округлению для того, чтобы заполнить «дыры».

COBOL был создан как язык, в котором, по умолчанию, используются числа с фиксированной точкой. Но значит ли это, что COBOL лучше современных языков подходит для выполнения математических вычислений? Если мы зацепимся за проблему наподобие результата вычисления значения 0.1+0.2 — то может показаться, что на предыдущий вопрос надо ответить «да». Но это будет скучно. Поэтому давайте пойдём дальше.

Мы собираемся поэкспериментировать с COBOL, используя так называемое рекуррентное соотношение Мюллера (Muller’s Recurrence). Жан-Мишель Мюллер — это французский учёный, который, возможно, сделал важнейшее научное открытие в сфере информационных технологий. Он нашёл способ нарушить правильность работы компьютеров с использованием математики. Я уверена, что он сказал бы, что изучает проблемы надёжности и точности, но нет и ещё раз нет: он создаёт математические задачи, которые «ломают» компьютеры. Одна из таких задач — это его рекуррентная формула. Выглядит она так:


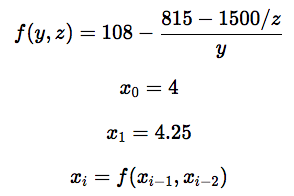
Этот пример взят отсюда

Формула совсем не кажется страшной. Правда? Эта задача подходит для наших целей по следующим причинам:

  • Тут используются лишь простые правила математики — никаких сложных формул или глубоких идей.
  • Мы начинаем с числа, имеющего две цифры после десятичной точки. В результате легко представить себе то, что мы работаем со значениями, представляющими некие денежные суммы.
  • Ошибка, которая получается в результате вычислений — это не маленькая ошибка округления. Это — отклонение от правильного результата на целые порядки.

Вот небольшой скрипт на Python, которые вычисляет результаты рекуррентного соотношения Мюллера, используя числа с плавающей и фиксированной точкой:

from decimal import Decimal
def rec(y, z):
 return 108 - ((815-1500/z)/y)
 
def floatpt(N):
 x = [4, 4.25]
 for i in range(2, N+1):
  x.append(rec(x[i-1], x[i-2]))
 return x
 
def fixedpt(N):
 x = [Decimal(4), Decimal(17)/Decimal(4)]
 for i in range(2, N+1):
  x.append(rec(x[i-1], x[i-2]))
 return x
N = 20 
flt = floatpt(N)
fxd = fixedpt(N)
for i in range(N):
 print str(i) + ' | '+str(flt[i])+' | '+str(fxd[i])

Вот что получается в результате работы этого скрипта:

i  | floating pt    | fixed pt
-- | -------------- | ---------------------------
0  | 4              | 4
1  | 4.25           | 4.25
2  | 4.47058823529  | 4.4705882352941176470588235
3  | 4.64473684211  | 4.6447368421052631578947362
4  | 4.77053824363  | 4.7705382436260623229461618
5  | 4.85570071257  | 4.8557007125890736342039857
6  | 4.91084749866  | 4.9108474990827932004342938
7  | 4.94553739553  | 4.9455374041239167246519529
8  | 4.96696240804  | 4.9669625817627005962571288
9  | 4.98004220429  | 4.9800457013556311118526582
10 | 4.9879092328   | 4.9879794484783912679439415
11 | 4.99136264131  | 4.9927702880620482067468253
12 | 4.96745509555  | 4.9956558915062356478184985
13 | 4.42969049831  | 4.9973912683733697540253088
14 | -7.81723657846 | 4.9984339437852482376781601
15 | 168.939167671  | 4.9990600687785413938424188
16 | 102.039963152  | 4.9994358732880376990501184
17 | 100.099947516  | 4.9996602467866575821700634
18 | 100.004992041  | 4.9997713526716167817979714
19 | 100.000249579  | 4.9993671517118171375788238

Вплоть до 12 итерации ошибка округления выглядит более или менее незначительной, но потом начинается настоящий ад. Вычисления с плавающей точкой сходятся к числу, которое в двадцать раз больше того, что получается при вычислениях с фиксированной точкой.

Возможно, вы думаете, что маловероятно чтобы кто-то выполнял столь масштабные рекурсивные вычисления. Но именно это стало причиной катастрофы 1991 года, приведшей к гибели 28 человек, когда система управления ракетой Patriot неправильно рассчитала время. Оказалось, что вычисления с плавающей точкой случайно принесли немало вреда. Вот отличный материал о том, что, возможно, высокопроизводительные вычисления — это всего лишь более быстрый способ получения неправильных ответов. Почитайте эту работу в том случае, если вы хотите получить больше сведений об обсуждаемой тут проблеме и увидеть больше примеров.

Неприятность заключается в том, что объём оперативной памяти, который имеется у компьютеров, не бесконечен. Поэтому невозможно хранить бесконечное количество десятичных (или двоичных) позиций. Вычисления с фиксированной точкой могут быть точнее вычислений с плавающей точкой в том случае, если есть уверенность в том, что низка вероятность того, что понадобится больше чисел после точки, чем это предусматривает используемый формат. Если число в этот формат не поместится — оно будет округлено. Надо отметить, что ни вычисления с фиксированной точкой, ни вычисления с плавающей точкой не защищены от проблемы, которую демонстрирует рекуррентное соотношение Мюллера. И те и другие в итоге дают неверные результаты. Вопрос заключается в том — когда это происходит. Если увеличить число итераций в Python-скрипте, например, с 20 до 22, то итоговое число, полученное при вычислениях с фиксированной точкой, составит 0.728107. 23 итерации? -501.7081261. 24? 105.8598187.

В разных языках эта проблема проявляется по-разному. Некоторые, вроде COBOL, позволяют работать с числами, параметры которых заданы жёстко. А в Python, например, есть значения по умолчанию, которые могут быть настроены в том случае, если у компьютера есть достаточно памяти. Если мы добавим в нашу программу строчку getcontext().prec = 60, сообщив десятичному модулю Python о том, чтобы он использовал бы 60 позиций после точки, а не 28, как делается по умолчанию, то программа сможет без ошибок выполнить 40 итераций рекуррентного соотношения Мюллера.

Продолжение следует…

Уважаемые читатели! Сталкивались ли вы с серьёзными проблемами, возникшими из-за особенностей вычислений с плавающей точкой?

Комментарии (41)


  1. worldmind
    17.09.2019 17:16
    #20633239

    Я был лучшего мнения о Decimal, но выход есть, немного переписал код и добавил рацинальных чисел.


  1. CrushBy
    17.09.2019 17:55
    #20633443

    Ну в Java, например, для решения этой проблемы есть BigDecimal. А вообще, проблема настолько общеизвестна и известно как решаема, что не думаю, что задержки с переходом с COBOL'а связаны именно с этим.


    1. SADKO
      17.09.2019 20:15
      #20633985

      Ну, там ещё нюансы округления в операциях, но опять-таки ничего нерешаемого…
      … проблемы не в яп, а в узком кругозоре не стреляных программистов, это если за фин сектор говорить, в науке же бывает что и бородатые деды не в состоянии оценить глубины последствий от принятых допущений.


  1. Hemulo
    17.09.2019 19:21
    #20633799

    Интересно, как бы это выглядело бы в Lisp, в котором поддержка рациональных дробей есть «из коробки»?

    В своё время, когда я впервые столкнулся с Lisp-ом (а именно с диалектом Scheme, но и в Comon Lisp и в Clojure, всё вроде так же), меня очень впечатлило что работа с дробями там совершенно прозрачная.

    можно писать что-то типа:
    (+ 1/2 1/4 1/4) и получить 1
    или
    (+ 1 1/5 1/10) и получить 13/10
    ну и т.п.


    1. Pand5461
      17.09.2019 22:18
      #20634445
      +3

      Да и в Питоне можно (https://docs.python.org/3/library/fractions.html).
      Что будет — понятно. Будет "правильно" сходиться к 5, становясь всё медленнее с каждой итерацией по мере роста числителя и знаменателя.
      На самом деле, 100 для той дроби является также стационарной точкой, так что ответ не настолько неверен, как пытаются представить.


      Как выглядит в Julia с рациональной арифметикой:


      Заголовок спойлера
      muller(y, z) = 108 - (815 - 1500 / z) / y

function muller_seq(n)
    x = [4, 17//4]
    for i = 3:n
        push!(x, muller(x[end], x[end-1]))
    end
    x
end

let ms = muller_seq(25)
    for i in 1:25
        println("$i $(ms[i])")
    end
end

1 4//1
2 17//4
3 76//17
4 353//76
5 1684//353
6 8177//1684
7 40156//8177
8 198593//40156
9 986404//198593
10 4912337//986404
11 24502636//4912337
12 122336033//24502636
13 611148724//122336033
14 3054149297//611148724
15 15265963516//3054149297
16 76315468673//15265963516
17 381534296644//76315468673
18 1907542343057//381534296644
19 9537324294796//1907542343057
20 47685459212513//9537324294796
21 238423809278164//47685459212513
22 1192108586037617//238423809278164
23 5960511549128476//1192108586037617
24 29802463602463553//5960511549128476
25 149012035582781284//29802463602463553


      1. red_andr
        18.09.2019 00:09
        #20634717
        +2

        На самом деле это метод решения уравнений Мюллера. И находятся корни следующего уравнения:
        x3 — 108x2 + 815x — 1500 = 0
        У которого их три. Да, «правильный»: 5, другой как раз 100 и ещё один: 3. То есть, оба варианта вычислений дают правильное решение, если, конечно, задача состоит именно в нахождении корней. Кстати, в этом примере вариант с фиксированной точкой тоже сходится к 100 после 30 итераций. Всё зависит от числа знаков после запятой, то есть точности. Только вариант с fractions всегда будет давать 5. Так как метод Мюллера известен своими проблемами с уравнениями порядка три и выше, лучше на практике использовать более стабильные методы.


    1. Rigidus
      19.09.2019 14:43
      #20642121

      (defun rec (y z)                                                                   
  (- 108 (/ (- 815 1500) y)))                                                      
                                                                                   
(defun floatpt (N)                                                                 
  (let ((x (list 4 4.25)))                                                         
    (loop :for i :from 2 :to (+ N 1) :do                                           
         (setf x (append x (list (rec (nth (- i 1) x)                              
                                      (nth (- i 2) x))))))                         
    x))                                                                            
                                                                                   
(defun fixedpt (N)                                                                 
  (let ((x (list 4 17/4)))                                                         
    (loop :for i :from 2 :to (+ N 1) :do                                           
         (setf x (append x (list (rec (nth (- i 1) x)                              
                                      (nth (- i 2) x))))))                         
    x))                                                                            
                                                                                   
                                                                                   
(let* ((max 25)                                                                    
       (flt (floatpt max))                                                         
       (fxd (fixedpt max)))                                                        
  (format t "~%")                                                                  
  (loop :for i :from 0 :to max :do                                                 
       (format t "~%~2,'0d | ~30,20f  | ~30,20f"                                   
               i (nth i flt) (float (nth i fxd)))))

      =>

      00 | 004.00000000000000000000 | 004.00000000000000000000
      01 | 004.25000000000000000000 | 004.25000000000000000000
      02 | 269.17645000000000000000 | 269.17648000000000000000
      03 | 110.54480000000000000000 | 110.54480000000000000000
      04 | 114.19658000000000000000 | 114.19659000000000000000
      05 | 113.99843000000000000000 | 113.99843000000000000000
      06 | 114.00886000000000000000 | 114.00886000000000000000
      07 | 114.00831000000000000000 | 114.00831000000000000000
      08 | 114.00833000000000000000 | 114.00833000000000000000
      09 | 114.00833000000000000000 | 114.00833000000000000000
      10 | 114.00833000000000000000 | 114.00833000000000000000
      11 | 114.00833000000000000000 | 114.00833000000000000000
      12 | 114.00833000000000000000 | 114.00833000000000000000
      13 | 114.00833000000000000000 | 114.00833000000000000000
      14 | 114.00833000000000000000 | 114.00833000000000000000
      15 | 114.00833000000000000000 | 114.00833000000000000000
      16 | 114.00833000000000000000 | 114.00833000000000000000
      17 | 114.00833000000000000000 | 114.00833000000000000000
      18 | 114.00833000000000000000 | 114.00833000000000000000
      19 | 114.00833000000000000000 | 114.00833000000000000000
      20 | 114.00833000000000000000 | 114.00833000000000000000
      21 | 114.00833000000000000000 | 114.00833000000000000000
      22 | 114.00833000000000000000 | 114.00833000000000000000
      23 | 114.00833000000000000000 | 114.00833000000000000000
      24 | 114.00833000000000000000 | 114.00833000000000000000
      25 | 114.00833000000000000000 | 114.00833000000000000000


      1. mayorovp
        19.09.2019 15:10
        #20642261

        А разве функция fixedpt не должна называться по-другому?


        1. Rigidus
          19.09.2019 15:16
          #20642303

          Возможно, но я стремился быть ближе к Python-версии.

          Как показывает результат — CommonLisp не уступает COBOL


          1. mayorovp
            19.09.2019 15:19
            #20642327

            Если вы стремились быть ближе к Python-версии — то и использовать надо было фиксированную точку вместо рациональных чисел...


      1. Pand5461
        19.09.2019 17:10
        #20642955

        У вас не fixed-point, а рациональная аримфметика тут.
        И nconc прям просится, а лучше push и nreverse.


  1. dimsoft
    17.09.2019 20:10
    #20633973

    Я в прошлом веке, чтобы уйти за 32 битные числа переписал на символьное хранение значений переменных и вместо ограничения в 2^32 расширил возможности вычисления до 10^256


    1. mayorovp
      18.09.2019 09:49
      #20635443

      Это называется "длинная арифметика". Кстати, вы зря взяли основание 10, основание 109 работает куда быстрее.


      1. dimsoft
        18.09.2019 10:25
        #20635647

        Я просто от встроенных переменных перешел на хранения цифр числа как символов, а в символьную переменную входило 256 символов.


        1. mayorovp
          18.09.2019 10:33
          #20635689

          Наверное, вы имеете в виду строковую переменную, в символьную только одна цифра влезает. Да, так можно делать, но лучше всё-таки использовать массивы и основание 109. Так можно в той же самой памяти хранить числа до 109*64 = 10576, притом это будет работать намного быстрее.


          1. dimsoft
            18.09.2019 10:41
            #20635743

            Не совсем понял, как?


            1. mayorovp
              18.09.2019 10:55
              #20635807

              Судя по упоминанию "в символьную переменную входило 256 символов", речь идёт о Паскале.


              Так вот, вместо string надо использовать array [0..63] of longint, а дальше то же самое. Только надо не забывать приводить разряды к int64 перед умножением, чтобы не было переполнения.


              Если используется версия языка без int64 — надо использовать array [0..127] of integer и основание 10000.


  1. math_coder
    17.09.2019 21:17
    #20634241
    +1

    Так я не понял, они (эти самые некие программисты) что, пытались считать финансы, используя вычисления с плавающей точкой? Ну, тогда они некомпетентны как программисты, но разве это причина не переходить на Java?


    1. chieftain_yu
      18.09.2019 09:22
      #20635329

      Ну, есть и пользовательский софт с такой проблемой.


      Я пользуюсь одной программой учёта финансов. Платной.
      В ней есть функция расчета стоимости по цене и количеству. Вводишь, скажем, объем и цену за литр топлива — и оно показывает рубли и копейки.
      И как-то раз возникло у меня расхождение на копейку.
      Сверил банковскую выписку и расходы — совпадает. А копейки нет.


      В итоге выяснил, что если вбить в записи расхода ровно ту же сумму руками — копейка появляется. Сообразил, что хранят они все же не целые копейки, а дробные.


      Написал в поддержку, получил стандартный ответ на тему "нам очень важно ваше мнение, оно будет перенаправлено в первую освободившуюся мусорную корзину".


      Правда, возможно, они это в новой версии починили, но тратить кровные на выяснение мне жалко.


  1. abar
    17.09.2019 22:26
    #20634465
    +1

    Вопрос к аудитории — а зачем переписывать то, что работает? Если у вас есть на это аргументы, то работа в банке — не для вас.

    Знаю банк, в котором есть сервисы, написанные с 80-ых еще на Коболе и выполняют все поставленные перед ними задачи. Есть сервисы на голой энтерпрайзной Джаве ранних версий, написанные лет 10-15 назад, которые, как ни странно тоже выполняют все задачи, и обладают просто феноменальным запасом по прочности. И есть часть сервисов, написанных на последних версиях Джавы и Котлина, со всеми Спринг Бутами, Хибирнейтами, современными фреймворками для фронтенда и обернутые в докер. Эти сервисы призванны обслуживать сиюминутные потребности бизнеса и спроектированные кое-как. Угадайте, где быстрее всего тухнет код? Так что не в языке дело, совсем не в языке.


    1. eumorozov
      18.09.2019 09:46
      #20635427
      +1

      Думаю, проблемы наверняка есть. Например, высокая стоимость и низкая доступность разработчиков и инструментов. Сложность интеграции с современными системами. Сложность поддержки наверняка тоже очень высока, так как более, чем уверен, что никаких фреймворков для юнит-тестов или каких-либо других для КОБОЛа не существует, и так далее.


      Не удивлюсь, если они рады были бы освободиться от этой легаси, но никак не могут.


    1. xFFFF
      18.09.2019 11:49
      #20636111

      Всё развивается, и рано или поздно приходится дописывать новые фишки. Системы на коболе имеют типичные проблемы легаси кода. Через какое-то время разработчики уходят, и уже никто точно не знает, как это всё работает. Новых разработчиков найти сложно. Переписать всё на современные технологии получается вдвойне сложней.


    1. rinnaatt
      18.09.2019 12:07
      #20636195

      Я тоже думаю, что проблема не в языке, а в доступности квалифицированных разработчиков. COBOL — древний язык, значит на нём кодили опытные программисты изрядного возраста, а раньше в программисты шли подготовленные кадры с математическим образованием, и таких было большинство.
      Сейчас все эти новые языки программирования и фреймворки на них призваны упрощать процесс написания кода, и теперь кодить могут все кому не лень, и получаем, что большинство программистов обладает низкой квалификацией — отсюда и проблемы.


      1. lz961
        18.09.2019 12:52
        #20636457

        Вопрос со стороны, в чем проблема выучить COBOL и разобраться в применявшихся ранее практиках программирования?


        1. eumorozov
          18.09.2019 14:46
          #20637047
          +1

          В том что эта инвестиция времени во-первых, может не окупиться (спрос все равно ограниченный — работодателей по пальцам пересчитать на весь мир), во-вторых, это может оказаться ужасно скучным. Все равно что сейчас, например, самому шить себе одежду из звериных шкур. Сразу же возникнет желание плюнуть на это занятие и пойти в ближайший торговый центр.


          1. lz961
            18.09.2019 19:10
            #20638607

            Рассмотрим COBOL как часть ТЗ, почему бы нее потратить время на его изучение (а он вряд ли сильно отличается от того-же Паскаля в принципиальном плане) за счет работодателя? К тому же COBOL все-таки не аналог одежде из звериной шкуры — автор текста, по видимому, клонит к тому что принципиальным плюсом COBOL были вещественные типы с фиксированной точкой, которых нет ни в замшелом, но по прежнему эффективном Фортране (как с точки зрения написания кода для частых, но важных задач, так и с точки зрения производительности), ни в С, но которые могут быть достаточно эффективны с точки зрения производительности, а главное, незаменимы (по сути) в финансовых расчетах.


            1. eumorozov
              18.09.2019 19:28
              #20638689
              +2

              Не знаю. Есть вещи, которые просто неинтересны людям. Никто не любит работать с legacy-кодом. Потому что это скучно, это бесперспективно, потому что понимаешь, что вручную пыхтишь, чтобы реализовать закат солнца, который в других языках реализован уже 30 лет назад.


              И вообще, меня очень удивляет эта статья. По идее, если так уж было необходимо, то логику кодирования чисел COBOL можно было бы реализовать в любом современном языке программирования. Скорее всего, это просто никому не нужно — не стоит игра свеч. Просто ждут, когда умрут окончательно эти 15-20 оставшихся систем на коболе, да и все.


            1. 0xd34df00d
              19.09.2019 03:19
              #20639935

              Потому что за счёт работодателя лучше изучать что-нибудь другое.


      1. Keynessian
        18.09.2019 22:00
        #20639269

        COBOL — древний язык, значит на нём кодили опытные программисты изрядного возраста, а раньше в программисты шли подготовленные кадры с математическим образованием, и таких было большинство.
        Сейчас все эти новые языки программирования и фреймворки на них призваны упрощать процесс написания кода, и теперь кодить могут все кому не лень, и получаем, что большинство программистов обладает низкой квалификацией

        Учитывая, что даже на Хабре встречаются те, кто считает, что поскольку они знают фреймворк, то им не нужны ни высшее образование, ни даже математика.


  1. denisromanenko
    18.09.2019 02:47
    #20634887

    Всегда не понимал одного — уже более десяти лет развиваются всякие транспайлеры, позволяющие перевести на JS код из кучи языков и диалектов с самыми безумными фишками.


    А в банковском и государственном секторе все воют от того, что последний программист на коболе в округе умер в возрасте 93-х лет.


    Неужели нельзя сделать хорошо отлаженный транспайлер для кобола (язык то не развивается, статичный) — а уж он хоть из Lua пускай транспилирует.


    1. mayorovp
      18.09.2019 10:02
      #20635519

      Проблема транспайлера для Кобола — в том, что исходный код программы останется на Коболе, а именно этого и хочется избежать. Плюс, сам язык может быть сколько угодно устоявшимся — но транспайлер для него всё равно будет сырым и со своими возможными ошибками.


    1. kingleonfromafrica
      18.09.2019 10:35
      #20635707

      Это вообще первый самый очевидный вопрос в данном случае, но не всё так просто в крупных конторах :)


      В начале нулевых 2 (ДВА) года вели переговоры с крупным территориальным подразделение МВД о таком методе перехода на что то более современное чем их глюкавое ПО под DOS…
      Это не закончилось вообще ни чем — ни кто не взял на себя ответственность.


      Год назад я писал ПО для анализа статистических данных и формирования отчетности из СУБД написанной на FoxPro и используемой в колониях ФСИН…
      Когда то давно кто то весьма грамотно спроектировал структуру БД, но потом коллектив сменился и всё было обильно унавожено костылями типа хранения текстовой конкатенации ИНДЕКСОВ статей УК, по которым был осужден зэк, в поле основной таблицы. И это только один пример.
      Понятно, что всё глючило и тормозило, но разговор сейчас не об этом. Я сразу предложил переписать всё, реализовав хотя бы просто на Access. Там довольно всё очевидно и я озвучивал сроки в месяц на написание и месяц на отладку в полубоевом режиме.
      Всё всех устраивало, но вопрос так же точно подвис в воздухе и ни чем не закончился.


      По моему мнению суть проблемы тут в том, что руководители профильных подразделений в крупных конторах не имеют необходимой компетенции и поступают по принципу "работает — не трогай". А, меняется что то только если уж совсем всё просто падает.


    1. Keynessian
      18.09.2019 23:11
      #20639549

      Неужели нельзя сделать хорошо отлаженный транспайлер для кобола (язык то не развивается, статичный) — а уж он хоть из Lua пускай транспилирует.

      А с упомянутой в статье математикой как быть?
      Поменять всю математику на вызовы специальной библиотеки?


  1. Tsvetik
    18.09.2019 07:51
    #20635131

    Так какому число должно сходиться это соотношение, к 5 или к 100?


    1. GarryC
      18.09.2019 09:46
      #20635433

      x^3+108*x^2-815*x+1500=(x-3)*(x-5)*(x-100), так что к обоим сходится.


    1. mayorovp
      18.09.2019 09:51
      #20635459

      При строго указанных начальных значениях — к 5. Но при любой погрешности в них — к 100.


      1. GarryC
        18.09.2019 10:57
        #20635811

        Ну к 3 тоже должно устойчиво сходиться, все зависит от заданного направления.


        1. mayorovp
          18.09.2019 11:08
          #20635873

          Насколько я помню, там устойчивая точка только 100.


          1. GarryC
            18.09.2019 11:32
            #20635989

            Ну тогда очень неудачная рекурсия, в обоих точках ( 3 и 100) производная функции больше нуля и должны себя вести одинаково.


            1. mayorovp
              18.09.2019 11:39
              #20636039

              А при чём тут вообще производная многочлена?


              Если представить xi как отношение yi+1/yi, то быстро окажется что yi = a 3i + b 5i + c 100i, где коэффициенты a, b и c зависят от начальных условий. А отношение соседних членов этой последовательности в общем случае (т.е. при ненулевом c) сходится к 100.


  1. b360124
    18.09.2019 14:11
    #20636849

    Интересно, а как на Javascript можно решить задачку ?


    const floatpt = n => {
  const x = [4, 4.25];
  for (let i = 2; i < n; ++i) {
    x.push(rec(x[i - 1], x[i - 2]));
  }
  return x;
};

const N = 20;
const flt = floatpt(N);

flt.forEach((el, index) => console.log(index, el));