Значительная часть геофизических публикаций в "солидных" журналах используют широко известную поправку к гравитационным данным — редукцию Буге. И все глобальные модели гравики ее используют. Наверное, это что-то очень важное и основано на детально проработанной теории? Давайте посмотрим, как можно графически проиллюстрировать смысл этой поправки. На рисунке показана идеальная плоскопараллельная пластина радиусом 200км, применяемая для вычисления поправки Буге согласно определению:

Рисунок из книги К.Ф. Огородникова «На чем Земля держится», 1953 г.
Да, вы не ошиблись — это поправка для плоской Земли и она не имеет смысла для сферической Земли! Все цитаты ниже приведены из одного издания, указанного ниже в списке литературы.
Поправка за влияние рельефа «выравнивает» реальный промежуточный слой до идеализированной плоскопараллельной пластины. Полученная аномалия силы тяжести носит имя П. Буге (1698 – 1758).
Для съемок масштаба 1:50 000 и мельче радиус учитываемой области влияния рельефа местности при вычислении поправок должен быть равен 200 км.
Но почему так произошло? Ответ простой — так сложилось исторически:
Изначально измерения силы тяжести использовались только для геодезических целей. Пьер Буге (Pierre Bouguer), вероятно, впервые выполнил гравиметрические наблюдения, в экспедиции, организованной французской Академией наук в Перу в 1735–1743 гг. (Li, Gotze, 2001; Гравиметрия и геодезия, 2010).
Принятые процедуры обработки гравиметрических данных и вычисления аномалий Буге формализовались в 1920-1930-х гг., когда происходило становление гравиразведки как одного из геофизических методов исследования недр Земли. Съемки имели локальный характер, при обработке полевых данных допускались многочисленные упрощения, соответствующие точности измерительной аппаратуры. Формулы вычисления поправок (редукций) в наблюденные значения силы тяжести опирались на существующие в то время сведения о форме Земли, абсолютном значении силы тяжести и максимально облегчали вычислительные процедуры, выполнявшиеся вручную. Несмотря на допущения и упрощения, эти правила вычисления аномалий силы тяжести с минимальным изменением продолжают использоваться и в настоящее время для решения большого круга геолого-геофизических задач и включены практически во все отечественные учебники по гравиразведке, инструкции и ГОСТы (Инструкция ..., 1980; Гравиразведка, 1990; ГОСТ Р 52334-2005).
Может быть, результат оправдывает принятые допущения? Проверим корреляцию между Буге гравикой и топографией (рельефом, или DEM) для глобальной модели WGM2012. Согласно определению поправки Буге, мы ожидаем отсутствие корреляции для пространственного масштаба менее 200км (радиус вычисления поправки Буге):
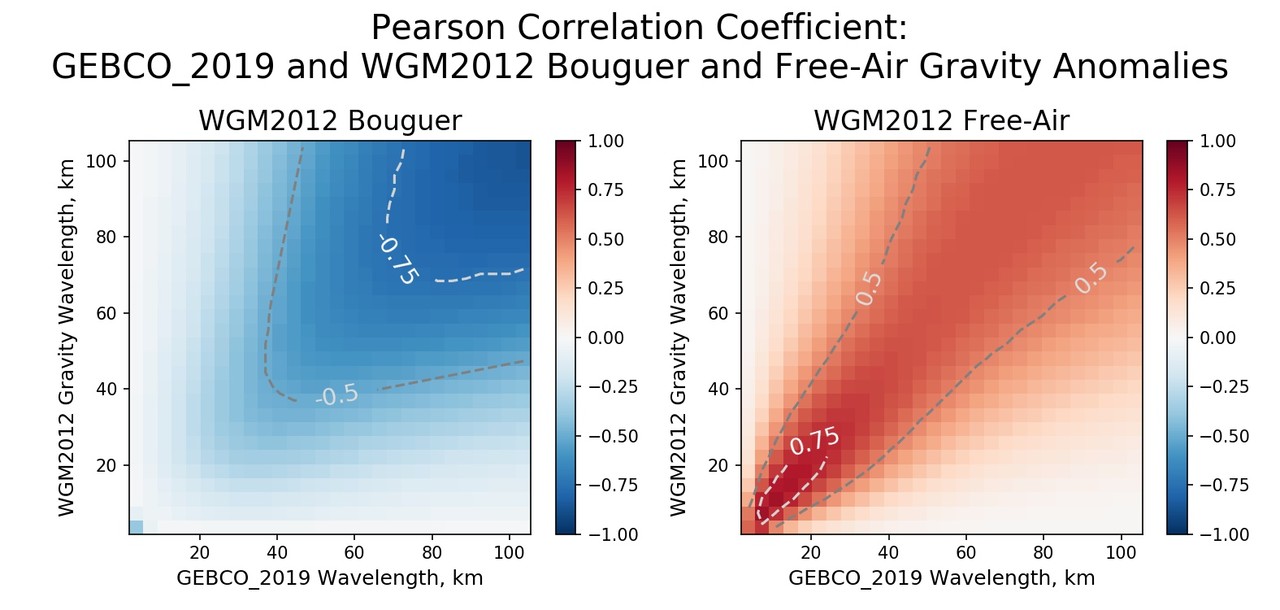
Оказывается, результат (с поправкой Буге) значительно коррелирован с топографией, начиная с масштаба 40км и высоко коррелирован с масштаба 80км — таким образом, результат полностью противоречит исходному определению.
Заметим, что также наблюдается высокая корреляция и для малых масштабов — это результат использования разномасштабных исходных данных (гравики и топографии) — они приведены к растрам одного разрешения, но пространственный спектр данных топографии в этой области вырожден. Это прямой результат принятого отношения к данным — в геофизике не принято проверять ни исходные данные, ни полученные результаты. Мне не удалось найти ни одной статьи по геофизике, где авторы озаботились бы проверить пространственные спектры исходных данных. Господа специалисты по data science — вас очень ждут и в этой индустрии!
Update Как мне подсказывают в комментариях, вопрос веры здесь и вообще дискуссионный. Сформулирую точнее: геофизики верят, что с точностью до миллиметров высоты в области радиусом 200км Земля плоская — так как только в этом случае при современной точности гравиметрических изменений обсуждаемая поправка применима. Лично для меня это означает ровно то, что написано в заголовке статьи!



MadridianFox
И всё же. Почему геофизики верят в плоскую землю? И верят ли?
N-Cube Автор
В статье дан ответ — верят, потому что так сложилось исторически. Как доказать, что верят? А потому, что используют именно поправку для плоской Земли. Для сферической Земли поправка Буге значительно отличается:
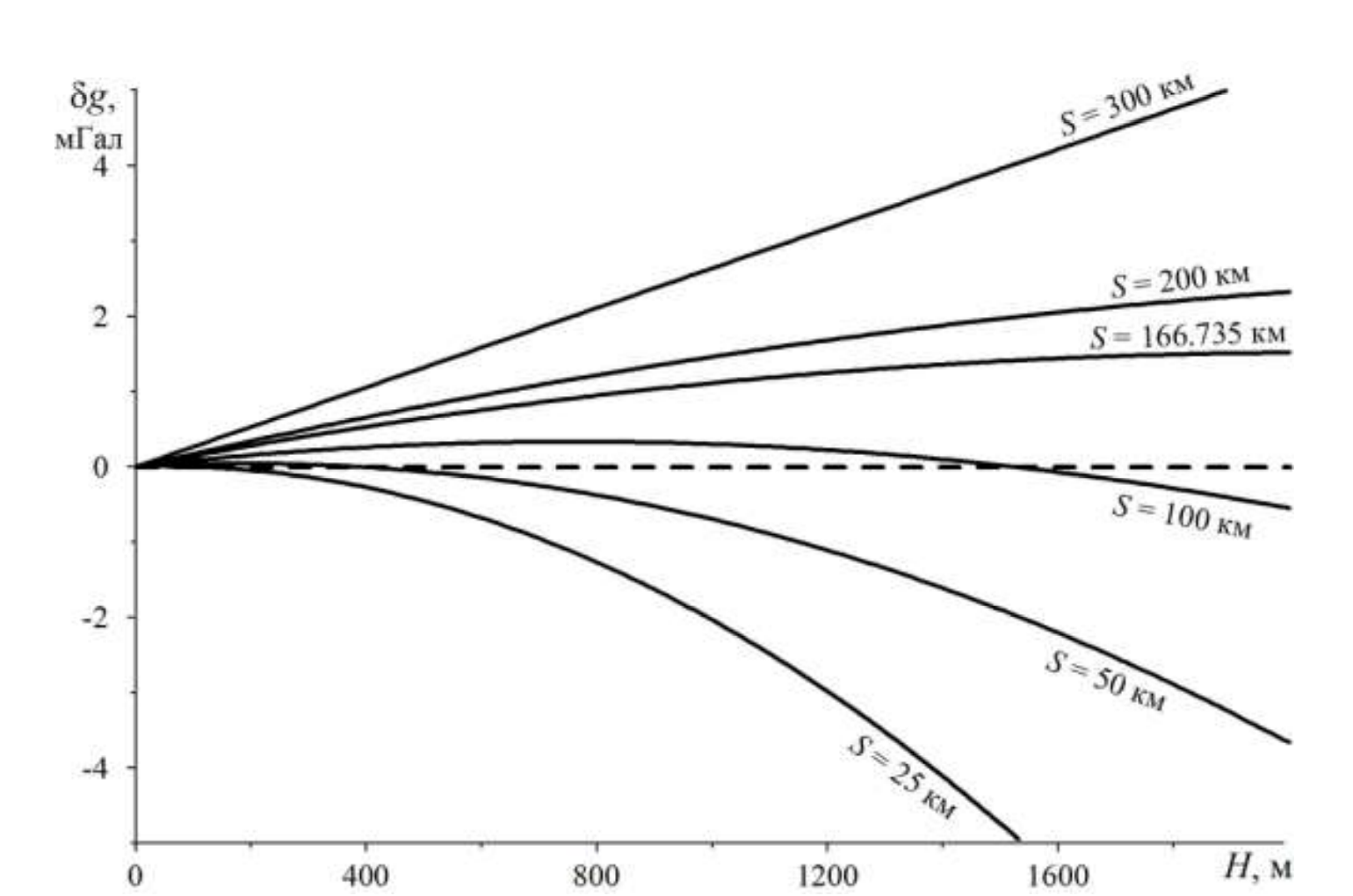
Рис. 1.8. Разность поправок за сферический и плоский промежуточный слой в зависимости от высоты пункта гравиметрических наблюдений (Бычков, С. Г., 2015)
Итак, по факту, геофизики верят в плоскую Землю, так как используют формулы для плоской Земли вместо сферической.