
Оптимизация в бизнесе в подавляющем числе случаев связана с применением метода линейного программирования. Метод достаточно понятен. Кроме того, имеется теорема существования и единственности решения.
Однако на практике все обстоит не совсем просто.
Первая проблема — это нелинейность реальных условий. Для того, чтобы метод линейного программирования можно было применить, они должны быть линеаризованы. Имеются способы правдоподобного задания нелинейности через линейные уравнения и неравенства за счет введения новых переменных, задания весовых коэффициентов и т.п. При решении производственных задач в этом случае необходимо оперировать большим количеством переменных и соответственно уравнений (неравенств).
В теории решения экстремальных задач имеется теорема об устойчивости решения задач линейного программирования. Согласно ей решение устойчиво только при условии выпуклости области определения задачи. При большом количестве переменных и неравенств установить, выпукла ли область определения задачи, не представляется возможным. При этом вероятность не выпуклости велика.
В случае если задача не устойчива, то в зависимости от начальной точки обхода вершин будет получаться разный результат.
Вторая проблема — ограничение переменной снизу (x>h>0). Любая реализация метода линейного программирования всегда обеспечит не нулевое значение x. Если x будет в точности равно h, то это означает, что значение переменной x по сути должно быть нулевым. На практике такие «фиктивные» объемы (эксцесс метода) разбрасывают по «содержательным» переменным. Следствие такой практики — эрозия понятия оптимального решения, что особенно важно, если такое решение одно из многих в цепочке решений.
Третья проблема — управленческая. Метод линейного программирования дает только один результат. А как посмотреть близкие результаты к оптимальному? Например, в полученном решении рейтинг поставщика плохой. Как понять, есть ли близкие решения, но для надежных поставщиков.
Транспортная задача
Пример соответствует транспортной задаче линейного программирования.
Имеется 5 перевозчиков (задача ставилась для перевозки угля), у которых действует двух тарифный расчет. Границы тарифов и сами тарифы можно менять (они заданы параметрически).

Перевозки задаются как точка-точка (по принятой методике при перевозке угля) и объем.
Общий вид интерфейса.

Область задания перевозок.
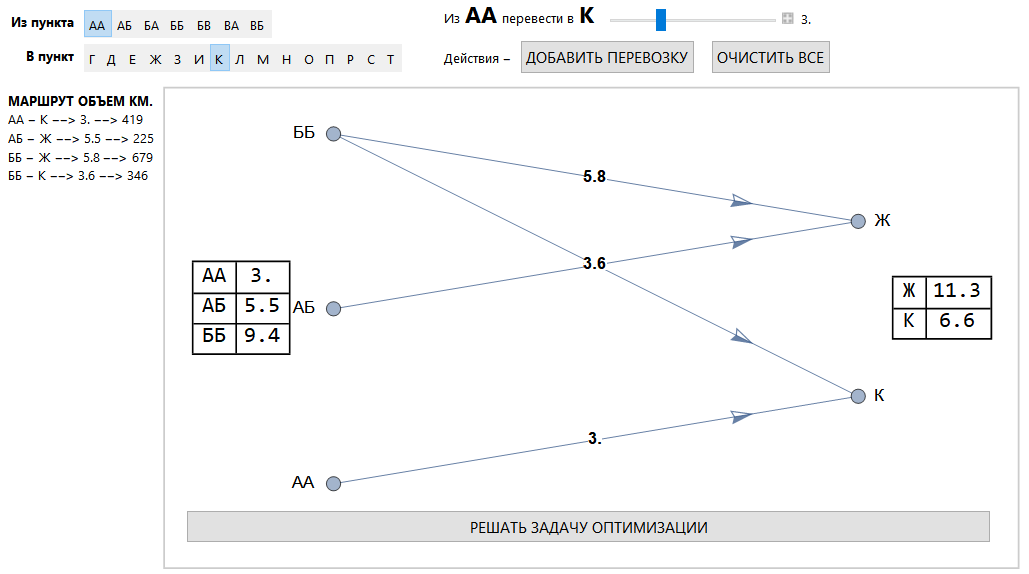
Кластерный метод решения
Вместо одной задачи линейного программирования решается кластер задач, количество которых соответствует всем возможным сочетаниям тарифов. В приведенной выше перевозке их 127 (второе значение в верхнем левом прямоугольнике).

Оптимальные решения выбираются из совокупности оставшихся корректных задач. Каждая задача дает оптимальное решение для конкретного сочетания тарифов. Выведенные выше решения составляют некоторый диапазон максимумов.
Чем хорош кластерный метод:
- появляется понимание устойчивости решения.
- нет «фиктивных» объемов по переменным, ограниченным снизу, так как будет существовать другое сочетание, где такое условие отсутствует (так как такая переменная отсутствует).
- можно вводить субъективные условия (рейтинги, предпочтения) в рамках применения стандартного метода линейного программирования.
При большем количестве перевозок имеем следующую картину (фрагмент).
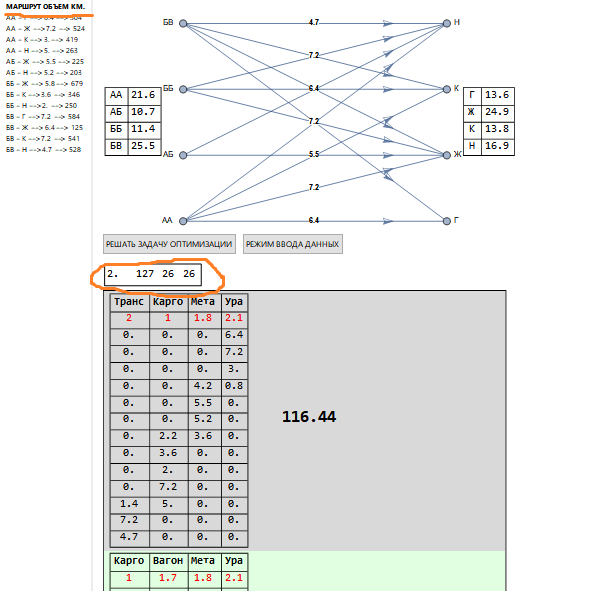
В верхнем левом углу в прямоугольнике над решениями (выделено оранжевым) указаны другие величины, чем ранее: 127 — сочетаний (как и раньше, что связано со структурой тарифных сеток), 26 — соответствует количеству оставшихся корректных задач, которые решаются. Под названием фирмы-перевозчика красным указан используемый тариф, а столбцы перевозок соответствуют перечню маршрутов (подчеркнуто оранжевым).
Важно отметить, что применяемый метод позволяет понять полученный результат, оценить аналогичные решения и использовать свой профессиональный опыт при выборе альтернатив, учитывая тонкости ведения конкретного бизнеса.


malkovsky
Линейное программирование покрывает большой пласт задач, но не точно не большинство потребностей бизнеса. Как минимум можно посмотреть на стандартные пакеты для оптимизации и что они умеют. Вот например Gurobi поддерживает линейное, квадратичное и смешанное программирование. Вообще в науке линейное программирование сейчас подпадает под более широкий класс задач выпуклой оптимизации — для них работает тот же эффективный метод внутренней точки, собственно это помогло бы с вашей первой проблемой. Если хотите попробовать как-то применять выпуклую оптимизацию на практике, советую посмотреть на cvxpy/cvxopt. Отдельно стоит выделить оптимизационные пакеты для машинного обучения (tensorflow, pytorch,… ), они вообще работают с произвольными функциями, но без ограничений. Они заточены под другой пласт задач, но тоже более чем используются на практике.
Честно говоря, ни из картинок, ни из текста почти не понятно, чего вы вообще пытаетесь добиться. Все, что понял лично я — это то, что вместо одной оптимизационной задачи вы решали сразу несколько и за счет этого получили больше информации о возможных стратегиях закупки. Думаю, что довольно наивно считать это чем-то прорывным. Более того, я уверен, что многие проблемы можно было бы решить более детальным моделированием, например почему бы не добавить рейтинг поставщика в целевую функцию?
Что вы понимаете под устойчивостью? В задаче линейного программирования ограничения всегда задают выпуклое множество.
anonymous Автор
Сначала конкретные вопросы.
1. Для решения задачи использовалась WolframMathematica. Она «умеет» многое.
2. Добиваюсь преодоления проблем, обозначенных вначале.
3. Устойчивость в задаче линейного программирования — это получение одинакового результата вне зависимости от начальной точки и метода обхода вершин (по тексту было уточнено).
4. Почему любая система линейных уравнений и неравенств должна порождать выпуклую область?
5. Проблема и условия устойчивости. Васильев Ф.П., Иваницкий А.Ю. Линейное программирование (1998).
Философские вопросы.
1. Линейное программирование не покрывает большинство потребностей в бизнесе (я такое не писал — видно по ссылке). Более того, оно не соответствует сути большинства задач, подразумевающих наличие нелинейности. При этом оно распространено, так как более менее понятно. Работа показывает как не очень пригодным методом добиваться вполне полезных результатов.
2. Нельзя правильно использовать результат, который непонятно как получен. Получая «оптимальное» решение неким стандартным методом, вы, на самом деле, не знаете, что получили. Чтобы в бизнесе применять оптимальное решение оно должно быть: понятно для лица принимающего решения (связано с промежуточными результатами и интерфейсом взаимодействия в процессе вычислений), учитывать имеющуюся практику (это не только математическая задача) и получено несколькими разными (альтернативными) математическими методами.
malkovsky
Посмотрел в книге, там под устойчивостью подразумевается совершенно другое — как изменится решение, если мы немного поменяем параметры задачи. Вообще обычно это называется «Sensitivity analysis».
Потому что пересечение выпуклых множеств выпукло
Ну так используйте нелинейное!
Тут то в чем проблема? Если переменные задачи не имеют интерпретацию вида «купить у поставщика АА такой объем угля», «перевезти из пункта А в пункт Б столько то угля», то это не проблема математического метода, это проблема моделирования.
anonymous Автор
1. Пример не выпуклой области. Пусть на трех одинаковых переменных одно подразделение определяет то, что оно хочет достичь, а другое то, что оно хочет избежать. Пусть в итоге получаем два треугольника (выпуклые): «достичь» и «избежать». В итоге задача определена на пересечении двух треугольников — можно дорисовать возможные общие не выпуклые области.
2. Вторая проблема — это наличие интервальных ограничений для переменной (сверху и снизу или только снизу).
3. В больших компаниях производственно-коммерческие ограничения обычно связаны с 2-5 тысячами переменных. Исторически они привыкли к линейному программированию. Линейность метода психологически делает результаты для бизнеса более правдоподобными.
4. Любой метод оптимизации связан с необходимыми условиями и структурами данных, в которые надо «втиснуть» реальную задачу. Для одного метода обычно это удается сделать только для части сложной задачи. Поэтому при решении одной задачи приходится задействовать несколько подходящих методов (последовательно или параллельно). Если при этом помнить, что каждый алгоритм имеет особенности реализации (явные или подразумеваемые), то без использования альтернативных методов и проверок обойтись нельзя.
5. Нелинейность тоже надо формализовать. Если делать это с помощью производственных функций, то получаем одновременно математические проблемы устойчивости, связанные с возможными «шевелениями» параметров производственной функции (в том виде как Вы их увидели) и содержательные проблемы бизнеса — а так ли все обстоит на самом деле как задано в производственной функции?
6. Спасибо за комментарии. Когда привыкаешь к материалу, то часто пропускаешь важные позиции.
malkovsky
1. Предполагаю, что вы имеете в виду следующий пример: есть два треугольника с вершинами (0, 0), (2, 0), (0, 2) и (1, 1), (1, 0), (0, 1) соответственно; наша область — это пересечение первого треугольника и дополнения второго. Такая область действительно невыпукла, как и дополнение второго треугольника. Дополнение треугольника невозможно получить набором линейных неравенств.
2. Ну это точно никакая не проблема, если у вас задача в духе cx->min, Ax<=b, x>=h, то последнее ограничения можно просто добавить к Ax<=b. Ну или можно сделать замену y=x-h, тогда исходная задача переписывается в виде cy->min, Ay<=b+Ah, y>=0. В любом случае это какие-то азы приведения задачи к нужному виду (канонической или стандартной форме).
По поводу остального — вы приводите поверхностные выводы, понять которые без деталей невозможно. Я не понимаю, про какие «необходимые условия и структуры данных» и «формализацию нелинейности» вы говорите.
anonymous Автор
Теоретически Вы совершенно правы, совокупность линейных неравенств порождает выпуклую область, пустое множество или в некоторых местах открытую область (не выпуклую область).
Но построить и оценить область определения системы линейных неравенств больше 2-3 переменных (если не брать простые примеры при обучении студентов) достаточно проблематично. Алгоритмы линейной оптимизации начинают с некоторой вершины и следуют по прямой, заданной соответствующим уравнением, до следующей ближайшей точки пересечения (вершины), а не по вершинам итоговой гипотетической выпуклой области. Если по смыслу есть коллизия в условиях, как я описывал ранее, то алгоритм пойдет по периметру не выпуклой области.
malkovsky
Это называется Симплекс-метод, обоснование которого опирается на то, что набор линейных равенств и неравенств всегда задает выпуклый многогранник.