Привет, Хабр!

Не так давно писал в качестве pet-проекта гиперказуальную игру с примитивной механикой, а именно: максимально быстро и точно повторить кривую линию. Идея максимально простая, но задача сравнения двух кривых оказалась довольно интересной. В этой статье я опишу разные идеи, которые рассматривал (в основном провальные) и конечный вариант, к которому я пришел.

Что сравниваем?

Механика игры простейшая: на экране появляется произвольная кривая и надо провести по ней пальцем максимально точно. Поэтому мы можем заранее предполагать, что ориентация и размер кривых должны быть близки. Однако в кривых может быть разное количество точек, что необходимо учитывать при сравнении. Также нет смысла вводить ограничение на положение линии на экране, если игрок нарисует идентичную линию, но со смещением на 1см, то он все равно справился с задачей.

А что если сравнить интегралы?

Первая мысль была "почему бы просто не сравнить интегралы?". Логика была такой: если мы заранее знаем, что наши линии должны быть схожи по длине, то близость интегралов будет характеризовать близость формы линий. Конечно, в итоге мысль была совсем бредовая, но описать стоит.

Как известно, интеграл описывает площадь фигуры под графиком. Вычислить его можно несколькими методами численного интегрирования. Не буду тут расписывать все методы, все давно сделали за меня.

/**
* points - массив точек в формате [x1, y1, x2, y2,...]
*/
private fun integral(points: LinkedList<Float>): Double {
  var area: Double = 0.0

  val i: MutableIterator<Float> = points.iterator()
  val prevPoint = FloatArray(2)
  prevPoint[0] = i.next() as Float
  prevPoint[1] = i.next() as Float

  val point = FloatArray(2)

  while (i.hasNext()) {
    point[0] = i.next() as Float
    point[1] = i.next() as Float

    val integral: Double = integral(point, prevPoint)
    area += integral
  }

  return area
}

/**
* p1 - array [x1,y1]
* p2 - array [x2,y2]
*/
private fun integral0(p1: FloatArray, p2: FloatArray): Double {
  val dx = abs((p1[0] - p2[0]).toDouble())

  return (p1[1]+p2[1])*dx/2
}

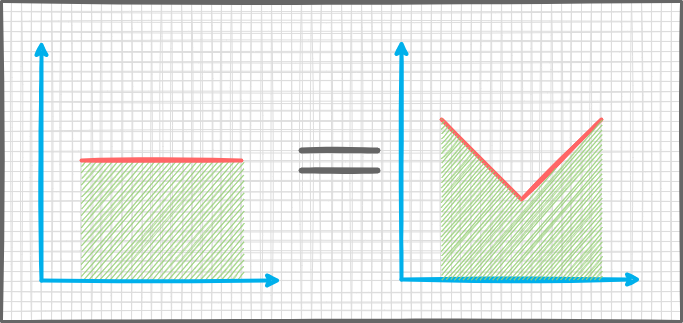
Проблема в том, что это не описывает реально форму кривой и не инвариантно к положению кривой на экране. И получается, что у линий ниже будет одинаковый интеграл, но их совсем нельзя назвать похожими по форме.

Триангуляция

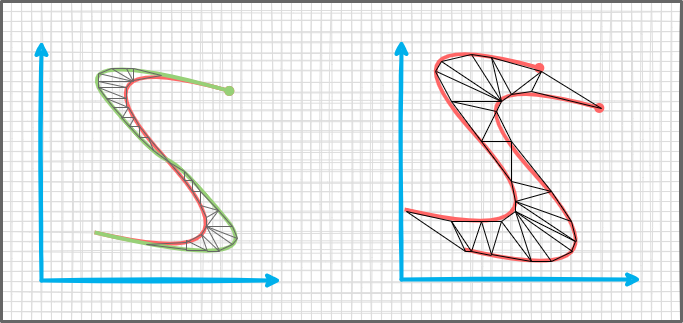
Вторым вариантом было построить триангуляцию фигуры, которая получится если соединить концы двух кривых. Чем меньше у нас будет площадь, получившейся триангуляции, тем ближе фигуры друг к другу по форме. Этот способ не инвариантен к масштабу и положению фигур на канвасе. Их необходимо центрировать, иначе площадь будет больше из-за смещения, как на рисунке ниже.

В целом этот способ должен работать для линий одного масштаба. Однако я от него отказался по двум причинам:

1. сложность реализации. Много краевых случаев при пересечениях кривых. Особенно, когда кривая пересекает сама себя.

2. сложно интерпретировать результат. Если мы хотим показать точность не в виде абсолютного значения площади, а в виде процента попадания, то необходимо выбирать какое-то максимальное пороговое значение площади, которое будем считать за полный промах (0% точности). Также площадь будет увеличиваться при увеличении длины линий, а значит порог должен быть относительным к масштабу.

Если будет проявлен интерес к этому методу, то напишу отдельную статью на тему триангуляции с реализацией, а пока идем дальше.

Сравнение направлений векторов между точками

Последним вариантом стало сравнение форм кривых через направление векторов от точки к точке. Этот метод будет описывать именно форму кривой, он инвариантен к масштабу, но чувствителен к ориентации кривой на плоскости. Ориентацию тоже можно учесть, но в нашем случае такого не требуется.

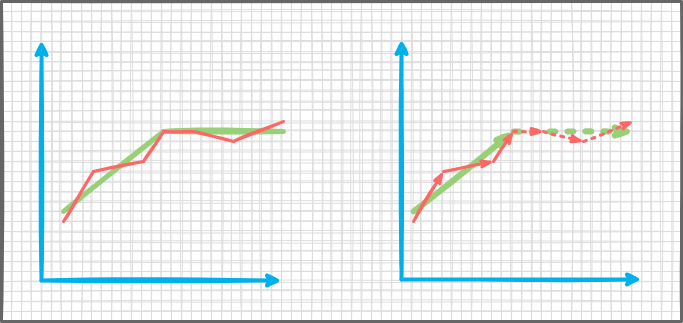
Опишем класс кривой с указанием относительного положения точки на кривой и направления кривой в этой точке. Учитывать относительное положение нам необходимо, поскольку в кривых может быть разное количество точек.

import java.util.*
import kotlin.math.abs

/**
* coordinates - массив точек в формате [x1, y1, x2, y2,...]
* asc - для определения направления обхода кривой, важно при сравнении направлений
*/

class Curve(val coordinates: LinkedList<Float>, asc: Boolean = true) {
    val points: LinkedList<Point> = LinkedList() //список точек кривой
    var length: Double = 0.0 //длина кривой

    init {
        val i: MutableIterator<Float> = if(asc) coordinates.iterator() else coordinates.descendingIterator()
        val prevPoint = FloatArray(2)
        if(asc) {
            prevPoint[0] = i.next() as Float
            prevPoint[1] = i.next() as Float
        } else {
            prevPoint[1] = i.next() as Float
            prevPoint[0] = i.next() as Float
        }
        val point = FloatArray(2)

      /*
      проходим по точкам и расчитываем угол направления кривой
      */
        while (i.hasNext()) {
            if(asc) {
                point[0] = i.next() as Float
                point[1] = i.next() as Float
            } else {
                point[1] = i.next() as Float
                point[0] = i.next() as Float
            }
            val distance = distance(prevPoint, point)
            if(distance < 10) continue
            length += distance

            var angle = StrictMath.atan2(
                (point[1] - prevPoint[1]).toDouble(), (point[0] - prevPoint[0]).toDouble()
            )

            if (angle < 0.0) angle = abs(alpha)

            points.add(
                Point(
                  point[0],
                  point[1],
                  length,
                  angle
                )
            )

            prevPoint[0] = point[0]
            prevPoint[1] = point[1]
        }
      
        val j: ListIterator<*> = diffs.listIterator()

        while (j.hasNext()) (j.next() as Point).dist /= length 
    }

    private fun distance(p1: FloatArray, p2: FloatArray): Double {
        val px = (p1[0] - p2[0]).toDouble()
        val py = (p1[1] - p2[1]).toDouble()
        return Math.sqrt(px * px + py * py)
    }

    data class Point(
      var x: Float, 
      var y: Float,
      var dist: Double, //percent distance from start
      val alpha: Double //atan
    )
}

Поскольку мы не знаем с какого конца игрок начал рисовать линию, то будем определять ближайший конец линии игрока к началу оригинальной линии. От этого будет зависеть направление обхода линии игрока. Поскольку длина кривых может быть разной, то мы будем учитывать относительное положение точек и проходить по двум кривым синхронно. Это значит, что если мы на Кривой1 попали на точку, соответствующую 10% пути, а на Кривой2 находимся еще в точке, соответствующей 5% пути, то двигаемся только по Кривой2, пока не пройдем 10% пути. Только после этого берем следующую точку на Кривой1. На рисунке выше сплошные вектора будут сравниваться со сплошными, пунктирные с пунктирными.

В итоге получается такая последовательность действий:

1. определяем ближайший конец линии игрока к началу оригинальной линии и начинаем обход с этого конца.

2. проходим по каждой линии синхронно, учитывая относительное положение точки каждой кривой.

3. Для каждой пары точек вычисляем разность направлений, нормированную на долю пройденного пути. И прибавляем полученную разность к суммарному отклонению.

4. после обхода всех точек нормируем итоговое отклонение на Пи и вычисляем точность.

5. Поскольку мне для игры было важно не только попадание в форму, но и размер кривой, то дополнительно вычисляется отклонение длины кривой игрока от оригинальной кривой.

private fun deltaAngles(alpha1: Double, alpha2: Double): Double {
    var dAlpha = StrictMath.abs(alpha1 - alpha2)
    if (dAlpha > StrictMath.PI) dAlpha = 2.0 * StrictMath.PI - dAlpha
    return dAlpha
}

/**
* curve1 - массив точек оригинальной кривой в формате [x1, y1, x2, y2,...]
* curve2 - массив точек второй кривой в формате [x1, y1, x2, y2,...]
*
* return - DoubleArray [Form Accuracy, Length Accuracy]
*/
fun compareCurves(curve1: LinkedList<Float>, curve2: LinkedList<Float>): DoubleArray {
    if (curve1.isEmpty() || curve2.isEmpty())
        throw IllegalStateException("curve can't be empty")

    //определяем начало исходной кривой и оба края нарисованной кривой
    val xc1: Float = curve1.get(0)
    val yc1: Float = curve1.get(1)

    val xc2: Float = curve2.get(0)
    val yc2: Float = curve2.get(1)

    val x2c2: Float = curve2.get(curve2.lastIndex - 1)
    val y2c2: Float = curve2.last
  
    //находим расстояние между началом исходной кривой и краями нарисованной кривой
    val mod1 = (xc1 - xc2) * (xc1 - xc2) + (yc1 - yc2) * (yc1 - yc2)
    val mod2 = (xc1 - x2c2) * (xc1 - x2c2) + (yc1 - y2c2) * (yc1 - y2c2)

    val c1 = Curve(curve1)
    //исходя из того, какой край ближе к началу, с него и начинаем обход нарисованной кривой
    val c2 = Curve(curve2, mod1 <= mod2)

    val i1: ListIterator<*> = c1.points.listIterator()
    val i2: ListIterator<*> = c2.points.listIterator()
    var point1: Curve.Point = i1.next() as Curve.Point
    var point2: Curve.Point = i2.next() as Curve.Point
    var diff = 0.0

    var currentDistance: Double = StrictMath.min(d1.dist, d2.dist) //относительное расстояние, которое уже прошли
    var prevDistance = 0.0
    while (currentDistance <= 1.0) {
        val d = currentDistance - prevDistance
        diff += deltaAngles(
            point1.angle,
            point2.angle
        ) * d

        if (currentDistance == 1.0) break

        if (point1.dist <= currentDistance) {
            point1 = i1.next() as Curve.Point
        }
        if (point2.dist <= currentDistance) {
            point2 = i2.next() as Curve.Point
        }

        prevDistance = currentDistance
        currentDistance = StrictMath.min(point1.dist, point2.dist)
    }
    
    val result = DoubleArray(2)
    result[0] = 1 - diff / Math.PI
    result[1] = 1 - abs(c1.length - c2.length) / c1.length
    return result
}

Заключение

В результате получился метод сравнения кривых, позволяющий оценить точность в процентах, инвариантный к масштабу. Потестить работу алгоритма и поиграть можно на андроиде тут Touch The Line