
Представьте, что в
Посмотрим, как построить модель ранжирования множества игроков (рекомендаций, результатов поиска
Теоретически задача не должна стать слишком сложной: пусть игроки сыграют несколько раз и посмотрят на соотношение побед. Но, к сожалению, этот естественный подход неидеален. Вот почему:
- нельзя определить, что именно значит близкое к 100% соотношение побед: или игрок исключительный, или ему проиграли только слабые соперники;
- если игрок сыграл всего несколько игр, то в оценке его силы высока неопределённость. При «сыром» соотношении побед этой проблемы нет.
Задачи, которые формулируются как игры «один на один», часто встречаются при ранжировании. Это касается:
- игроков в реальном соревновании: теннис, гонки, карточные игры, бои покемонов
и т. д. - результатов поиска: чем они релевантнее запросу пользователя, тем лучше;
- рекомендаций: чем они релевантнее тому, что пользователь захочет купить, тем лучше,
и т. д.
Давайте при помощи PyMC создадим простую байесовскую модель, где решается эта задача ранжирования. Подробности о модели смотрите в моём введении в байесовский мир с PyMC — предшественником PyMC с почти таким же синтаксисом.
Модель Брэдли — Терри
Придадим этой модели байесовское звучание. Пугающее, но на самом деле очень простое.
Что это за модель?
Вся эта модель сводится к двум допущениям:
- У каждого игрока (человека, покемона) есть сила игры, у результата поиска и рекомендации — релевантность и так далее.
- Если соревнуются игроки 1 и 2, сила которых s₁ и s₂ соответственно, игрок 1 выигрывает с такой вероятностью:

σ — наша старая добрая сигмоида
Причём никаких признаков (характеристик) игроков вроде роста или веса человека здесь не используется. А значит, эта модель применима к разным задачам.
Если включить в неё характеристики игроков, то можно получить
x явным образом построить численные значения силы игроков s = f(x), авторы RankNet используют нейросеть, а в байесовском подходе силы s напрямую работают как параметры.Чтобы построить частотную версию модели Брэдли — Терри при помощи фреймворка глубокого обучения, можно использовать слой встраивания. Давайте проверим работоспособность такого построения модели. Итак, у каждого игрока есть сила. По ней и упорядочиваются игроки.
Допустим, у первого игрока сила намного больше, чем у второго, то есть s₁ — s₂ — это большое число. Значит, σ(s₁ — s₂) близко к единице. Таким образом, с огромной вероятностью выиграет первый игрок. Именно это нам здесь и нужно. В обратной ситуации — аналогично. Если у игроков сила одинакова, вероятность выигрыша каждого из них равна σ(0) = 50%. Идеально.
Создание набора данных
Прежде чем строить модель, создадим искусственный набор данных о результатах игр:
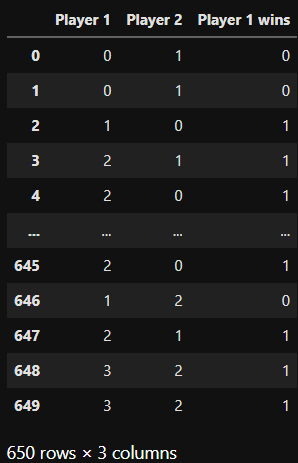
И теперь у нас есть преимущество: нам известны признаки, которые нужно искать в модели.
Вот код генерации искусственных данных:
import pandas as pd
import numpy as np
np.random.seed(0)
def determine_winner(player_1, player_2):
if player_1 == 0 and player_2 == 1:
return np.random.binomial(n=1, p=0.05)
if player_1 == 0 and player_2 == 2:
return np.random.binomial(n=1, p=0.05)
if player_1 == 1 and player_2 == 0:
return np.random.binomial(n=1, p=0.9)
if player_1 == 1 and player_2 == 2:
return np.random.binomial(n=1, p=0.1)
if player_1 == 2 and player_2 == 0:
return np.random.binomial(n=1, p=0.9)
if player_1 == 2 and player_2 == 1:
return np.random.binomial(n=1, p=0.85)
games = pd.DataFrame({
"Player 1": np.random.randint(0, 3, size=1000),
"Player 2": np.random.randint(0, 3, size=1000)
}).query("`Player 1` != `Player 2`")
games["Player 1 wins"] = games.apply(
lambda row: determine_winner(row["Player 1"], row["Player 2"]),
axis=1
)Набор состоит из данных о трёх игроках, которые соревнуются друг с другом случайным образом. Именно это происходит в функции
determine_winner: принимается два индекса игроков (0, 1, 2) и вывод показывается, если выигрывает player_1. Пример: в игре (0, 1) игрок 0 выигрывает с вероятностью p=0.05 у игрока 1.Внимательно посмотрите на вероятности в коде: игрок 2 должен быть лучшим, 1 — средним, а 0 — слабейшим.
Для разнообразия введём четвёртого игрока, который сыграл всего две игры:
new_games = pd.DataFrame({
"Player 1": [3, 3],
"Player 2": [2, 2],
"Player 1 wins": [1, 1]
})
games = pd.concat(
[games, new_games],
ignore_index=True
)Игрок 3 сыграл дважды против номера 2 и даже дважды выиграл. Значит, у номера 3 значение силы тоже должно быть высоким. Но нельзя сказать, действительно ли он лучше номера 2 или это была случайность.
Построение модели при помощи PуМС
Теперь можно построить модель. Обратите внимание: силы игроков обозначаются априорными гауссовыми значениями. Кроме того, для пяти игроков в модели выводятся постериорные значения, хотя для последнего игрока с номером 4 данных нет. Посмотрим, как это происходит.
Что ещё важно — я не использую сигмоиду явно. Если передать разницу сил игры у игроков через параметрlogit_p, а неp, роль сигмоиды сыграет объектpm. Bernoulli.
import pymc as pm
with pm.Model() as model:
strength = pm.Normal("strength", 0, 1, shape=5)
diff = strength[games["Player 1"]] - strength[games["Player 2"]]
obs = pm.Bernoulli(
"wins",
logit_p=diff,
observed=games["Player 1 wins"]
)
trace = pm.sample()Проверим, как распределяются постериорные значения. Выше — апостериорные распределения в виде графиков плотности, ниже — лесовидная диаграмма [forest plot], на которой легко сравнивать постериорные значения силы:

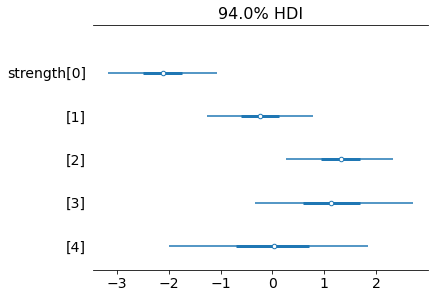
Смотрите: игрок с номером 0 действительно слабейший, за ним следует номер 1. Номера 2 и 3 — лучшие, как и ожидалось. Среднее апостериорного распределения у номера 3 чуть ниже, чем у номера 2. Зато интервал высокой плотности намного больше. То есть неопределённость в отношении силы номера 3 больше по сравнению с номером 2. Постериорное значение силы номера 4 такое же, как априорное. Оно нормально распределено со средним значением 0 и среднеквадратическим отклонением 1. Ничему новому модель здесь научить нельзя. Вот ещё цифры:

Похоже, в этом случае наблюдалось и хорошее схождение MCMC: все значения
r_hat равны 1.Кроме того, у некоторых игроков значение силы отрицательное, но это нормально, ведь мы всё равно используем разницу в силе только между двумя игроками. Если вам это по
HalfNormal или просто добавьте к постериорным значениям константу, например 5. Тогда все средние значения и интервалы высокой плотности окажутся в положительном диапазоне.Заключение
Модель начиналась с априорных представлений об уровнях силы игры, которые затем с помощью данных менялись. Чем больше сыграно игр, тем меньше неопределённость относительно силы игрока. В экстремальном случае, когда игроком не сыграно ни одной игры, апостериорное распределение его силы равно априорному, что логично.
Надеюсь, сегодня вы узнали что-то новое, интересное и полезное. Спасибо за внимание!
А мы поможем разобраться в программировании, чтобы вы прокачали карьеру или стали востребованным профессионалом в IT:
Чтобы увидеть все курсы, кликните по баннеру:

Краткий каталог курсов
Data Science и Machine Learning
Python, веб-разработка
Мобильная разработка
Java и C#
От основ — в глубину
А также
- Профессия Data Scientist
- Профессия Data Analyst
- Курс «Математика для Data Science»
- Курс «Математика и Machine Learning для Data Science»
- Курс по Data Engineering
- Курс «Machine Learning и Deep Learning»
- Курс по Machine Learning
Python, веб-разработка
- Профессия Fullstack-разработчик на Python
- Курс «Python для веб-разработки»
- Профессия Frontend-разработчик
- Профессия Веб-разработчик
Мобильная разработка
Java и C#
- Профессия Java-разработчик
- Профессия QA-инженер на JAVA
- Профессия C#-разработчик
- Профессия Разработчик игр на Unity
От основ — в глубину
А также

