Несмотря на то, что является неплохим таким развлечением на долгий вечер, как и многие настолки, имеет практическую пользу в обучении математике: помогает подружиться с концепцией графика функции или уравнения, играется в любом классе, начиная с седьмого; или младше - но тогда надо объяснить ученику идею координатной плоскости и линейной функции. Правила придуманы на основе классического морского боя.
В качестве игрового поля берётся координатная плоскость хОу произвольного размера. Если играющие знакомы с отрицательными числами, то от (-10; -10) до (10; 10) скорее всего будет достаточно, хотя чем обширнее их знания алгебры, тем больше нужна игровая площадь. Для всех, кто младше шестого класса, советую поле от (0; 0) до (20; 20), или даже до (10; 10). Прямоугольное, естественно (квадратность не обязательна). Для старших, конечно, можно задавать её как любую криволинейную трапецию или не задавать вовсе, лишь бы все корабли вместились в чертёж заданного масштаба.
Раскладка кораблей и подобные детали - как в стандартных правилах. Точно так же делаем у себя два поля (одно своё, одно противника). Можно играть "в открытую", показывая противнику свои корабли - это не сильно упростит ему жизнь, но сделает игру поучительнее.
Очерёдность ходов определяется стандартными правилами. А вот ходить можно по-всякому. Для семиклассников и младше всё просто: либо координаты точки, либо уравнение прямой (но - чтобы сходить, надо построить её график на поле противника). Продвинутые, естественно, могут использовать модули и кусочные функции. Дальше противник строит у себя этот же график и говорит, в каких точках поражены его корабли. Следует отметить, что если функция касается корабля, то он не ранен, и лишь если пересекает его - тогда ранен. Однопалубному кораблю достаточно одного пересечения для "убийства", четырёхпалубному - четырёх, и т.п., как в классических правилах.
Начиная с восьмого класса игра становится веселее и зрелищнее. Можно строить параболы и векторы! И гиперболы, конечно. А в десятом появляются синусоиды. Тангенсоиду применять нельзя - уж больно смертоносна она. Вообще, конечно, если игрок вспомнит, что sin10x хорошо так растягивается вверх, он и синусом всех убьёт, но лично я оставляю это как чит-код, догадаться до которого - похвально. Однако, конечно, запретить все периодические функции - правильная мысль. Здесь вводится ограничение - функцию каждого типа (квадратичную, линейную и так далее) можно использовать один раз в некоторое количество ходов, определяемое разнообразием функций в арсенале игроков; но, однако, лично я считаю разные способы задать линейную функцию как разные функции: можно задать "как обычно" (y = kx+b), можно как график уравнения (ax + by +c = 0), или можно использовать модуль или кусочную запись.
Получается довольно азартно, хотя и медленно. Часового занятия (играю с учениками, которых учу математике) не хватает на то, чтобы полностью разыграть партию, но как правило определяется побеждающая сторона. Можно играть по интернету с помощью онлайн-доски, поддерживающей множественные фреймы и выбор фона, например - google jamboard. Думаю, можно играть и в сингл-режиме, сначала создавая поле кораблей, а затем "раскатывая" его разными графиками.
На первом примере две модульные функции, окружность (заданная уравнением), синусоида, парабола и две линейных. Каждая сделана в отдельный ход, между модульными и обычными линейными - цикл в 4 хода.
На втором примере есть ещё и гипербола. Несложно заметить, что тут всего четыре графика против шести на предыдущем: играли онлайн, один игрок по невнимательности сделал ход против себя (перепутать фреймы несложно).
Комментарии (35)

Cheater
01.06.2023 19:37что sin10x хорошо так растягивается вверх, он и синусом всех убьёт
От sin10x можно спрятаться выше и ниже 1. А вот y = 1 / (4(x - 0.5 - [x])) убьёт всё живое...

amakhrov
01.06.2023 19:37+1`10 sin (10 x)` - растянем по вертикали

Tarakanator
01.06.2023 19:37+5Тоже об этом подумал. Предлагаю ввести френдлифаер для исключения таких функций.

Readme
01.06.2023 19:37+1Френдлифаер круто, ещё и стратегию меняет: по функции, названной противником, можно сделать предположения, куда он не хочет попасть сам.

Kerrigan
01.06.2023 19:37+2Очень напомнило игру Graphwar, только там не морской бой, а Scorched Earth

Refridgerator
01.06.2023 19:37+14А можно тоже поучаствовать?:)
 Функция
Функция(3887661586079176627680+x*(-3595714078112483053104+x*(907114120857784628034+x*(140341883742853062275+x*(-113414717390212672849+x*(20459558278721114367+x*(-877719830593774547+x*(-80901590722858703+x*(-18172144619884101+x*(6463598063744701+x*(-383419713461339+2*x*(-30321401247636+x*(6083611426165+4*x*(-119550100523+3*x*(1686073133+120*x*(-314431+2910*x))))))))))))))))/(268087948029158322240+2*x*(-134233534276429388976+x*(53399207805273977838+x*(-8807207536828369757+x*(-87551315669396298+x*(101980258296392797+x*(71967616845042386+x*(-29517988634013803+x*(4156601506349900+x*(-98837085786909+2*x*(-22084677732110+3*x*(962769636040+x*(-35348711357+44*x*(-50107863+x*(6287989+120*x*(-2063+30*x))))))))))))))))

semmaxim
01.06.2023 19:37+2О! Киньте в меня, как это делается и с помощью чего. Не, я понимаю, что тут по нескольким точкам строится функция. Но интересует конкретная математика и программа :)

Refridgerator
01.06.2023 19:37+2Метод называется Barycentric Rational Interpolation, подробнее можно почитать здесь, готовая реализация есть в boost и на питоне тоже попадалась. А рисовал в Wolfram Mathematica.

pehat
01.06.2023 19:37+2Интерполяционный многочлен Лагранжа можно руками выписать, и без астрономических чисел.

Refridgerator
01.06.2023 19:37Это очевидно НЕ многочлен Лагранжа, поскольку у того отсутствует знаменатель. Но вы, конечно же, можете сделать свой вариант решения, а мы сравним. Функцию в студию!

Refridgerator
01.06.2023 19:37А интерполяционный многочлен Лагранжа, который часто вспоминают в подобных случаях, имеет пару особенностей, которые делают его совершенно непригодным для использования на практике. Это:
а) высокий уровень "неожиданных" пульсаций (в англоязычных источниках часто формулируется как wild oscillations),
б) квадратичная сложность,
в) численная неустойчивость.
Причём это характерно не только для многочленов Лагранжа, но и для полиномиальной интерполяции в целом. Поэтому на практике его вы не встретите, зато встретите (би)кубическую интерполяцию и сплайны Безье, а для высоких порядков используются специальным образом сконструированные многочлены и в первую очередь конечно же Чебышева (не могу не заметить по случаю, что Чебышев — исконно русский математик, как и Бернштейн, который создал мат.аппарат для кривых Безье задолго до то того, как те получили своё название).А про барицентрическую интерполяцию мало кто знает только потому, что это в прямом смысле край математической науки — то, что придумывается и развивается прямо сейчас. И даже не потому, что последние исследования на эту тему датируются 2023 годом — а потому, что последние открытия в этом направлении вообще нигде не опубликованы и о них знают 1.5 человека (ну а товарищи из Википедии и тем более, которые до сих пор не удосужились создать статью по теме).
P.S. Как это часто бывает в математике, название "барицентрическая" отражает идею, но не суть. А по сути — это интерполяция гиперболами, которые располагаются в узлах интерполянта.

youngmysteriouslight
01.06.2023 19:37+1Спасибо, интересная идея.
Хочу на практике попробовать с кривыми Безье и эллипсами. Кстати, они не имеют обсуждаемых выше проблем массового поражения.

belch84
01.06.2023 19:37+2Тоже хочу себя попробовать. Полиномы Чебышева, соответствующим образом масштабированные, решат задачу уничтожения кораблей противника за один ход. При этом не требуется никаких особых знаний, полиномы конструируются из элементарных функций, Wolfram Mathematica тоже не нужен. Вот формула для полинома порядка n:
 Полином Чебышева порядка 10
Полином Чебышева порядка 10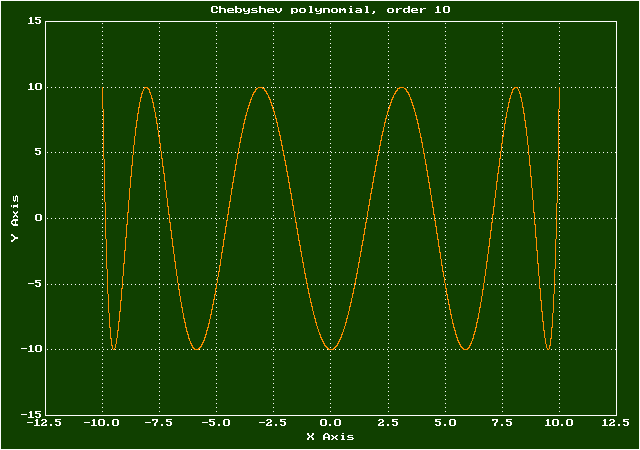
Полином Чебышева порядка 30
Полином Чебышева порядка 1000000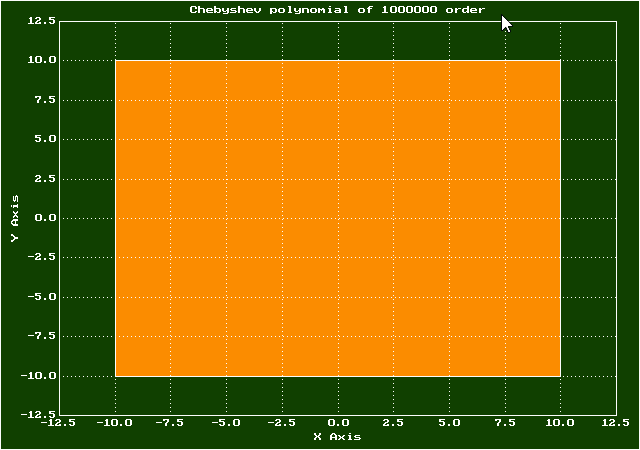
В последнем случае у полинома 1000000 корней на интервале, поэтому он гарантировано пройдет через все корабли противника, даже множество раз. И сами по себе эти полиномы не периодические. Разумеется, запрет использовать именно косинусы (или арккосинусы) сделает этот вариант невозможным
Refridgerator
01.06.2023 19:37+1Чебышева интереснее в параметрическом виде использовать, чтобы устраивать «ковровую бомбардировку»:

Но мне это показалось не совсем честным решением.

khe404
01.06.2023 19:37+1Вообще идея очень интересная
Предлагаю следующее развитие сюжета которое понизит важность периодических функций.
Попаданием считать точку пересечения двух функций например в центре заданного квадрата
Стрелять можно только из положения своих живых кораблей.
-
возможность на любой выстрел ответить: отбил.
Тогда поражающая функция симметрично рисуется на поле стрелявшего противника, но с ограничением в пропуск хода если функция не принесла никакого попадания.
Таким образом периодические функции резко теряют в привлекательности, так как с большой вероятностью ранят корабли противника.

stepuncius
01.06.2023 19:37sin(1000/x) - я победил?

Refridgerator
01.06.2023 19:37Автор же намекнул, что синус неспортивно. Но если можно возводить функцию в степень, то можно так.

lgorSL
01.06.2023 19:37+1Вспомнил такую штуку, хоть она и очевидно ломает игру. https://ru.m.wikipedia.org/wiki/Кривая_Пеано

RikoMinase
01.06.2023 19:37+1Для того, что бы стороны не использовали "ковровые бомбардировки", нужно играть на одном игровом поле, с френдлифаером

smackred
01.06.2023 19:37+1А как вам такая идея: "корабли" задаются не стандартными формами, а тоже функциями, с ограничениями по площади? Правда, затянется ещё больше и это уже для самых продвинутых, тех, кто знаком с высшей математикой.

busheisha Автор
01.06.2023 19:37+2Я честно говоря сильна только в школьной математике)) Высшую я могу на уровне "если мне объяснить, то я пойму". Я тут поняла, что можно математически вводить уравнениями границы кораблей, а играть тогда как-то попроще, тогда будет всё ещё динамично, и знакомство с высшей математикой не потребуется...
У меня есть ограничение по времени - за час урока надо успеть разобраться с правилами, значительно поиграть и получить удовольствие. Ну и чтобы я могла человека многому научить в формате игры.
Однако есть это какая-то тусовка условно взрослых условно математиков (кому просто по приколу в такое играть) и нет цели решить образовательную задачу в краткие сроки, звучит очень круто
Refridgerator
01.06.2023 19:37+1Вы молодец. Мало кто из учителей математики в школе выкладывается на то, чтобы действительно заинтересовать детей и простимулировать их к не просто обучению, а к пониманию того, что математика — действительно царица всех наук, а иногда даже чёрная магия, которая позволяет сделать немыслимое для всех прочих.

busheisha Автор
01.06.2023 19:37Спасибо! В школу я никак не попаду - зовут только в московские, а живу в Уфе (чтоб работать в госке, нужно спец. образование, его у меня нет), отрываюсь на индивидуальном обучении. Ну и стараюсь что-то полезное продуцировать. Сейчас пишу фанфик по ГарриПоттеру с максимально зазывающим для подростков сюжетом, где между строк пытаюсь рассказывать про математику. Такой приём позволит рассказать хорошее о математике большему количеству детей, причём после написания - вполне пассивно, без увеличения нагрузки вследствие количества обучаемых

bbogatyrov
01.06.2023 19:37Сегодня поиграл с сыном. Автору большое спасибо за идею. На первом этапе мы сначала рисовали функции (прямая + окружность), под них писали формулы. Как рука набьется - будем оперировать формулами.
для любителей ВМ: если без компьютера вижу вариант бить производной первого порядка (в школе все делается через дискриминаты). Да, синус /косинус имхо применять можно с ограничением 2-3 периода на поле

busheisha Автор
01.06.2023 19:37Как круто, я рада что кто-то уже опробовал игру, и она принесла пользу! :)









DedulyaP
Очень интересная идея использовать этот подход в образовательных мероприятиях. Рождается вопрос для размышлений: Какова верная победная стратегия скорейшей победы в различных условиях (можно накладывать ограничения на использование смертоносных функций)? Круто, что Вы заметили такую математическую задачу в простой детской игре.
LuchS-lynx
Мой одноклассник примерно в 8-9 классах занимался этой проблемой с учетом тер.вера, в итоге самое оптимальное решение это делать шаг из выстрелов самый длинный корабль минус одна клетка, в общем случае конечно