В этой статье продолжим тему решения криптографических задач с ресурса MysteryTwister. И сегодня на очереди любопытный шифр, далёким предком которого является квадрат Полибия. Мы познакомимся с трёхраздельным шифром Феликса Деластеля. Что интересно информации об этом энтузиасте  криптографии очень мало в английском и французском сегментах сети (Деластель — француз), а в русскоязычном о нём почти нет совсем, хотя наверняка человеком он был очень неординарным. Почему я так решил? Да потому, что Феликс Деластель по роду профессиональной деятельности не имел к криптографии совершенно никакого отношения, поскольку всю жизнь проработал в порту Сен-Мало и криптографией занимался факультативно. Тогда как ранее и позже криптография была уделом учёных, профессиональных военных и дипломатов. Биографических данных о нём очень мало, но одно известно точно: на рубеже XIX и XX веков Деластель написал книгу "Traite Elementaire de Cryptographie" (Базовый трактат по криптографии), в которой он описывал системы шифрования, которые создал.

Одним из шифров, разработанных Деластелем, является трёхраздельный шифр (Trifid cipher), использующий таблицы для разделения каждой буквы открытого текста на триграмму. Что интересно, в этом шифре используется транспозиция совместно с дроблением для скрытия статистической взаимосвязи между зашифрованным и открытым текстом. Его предшественник — двунаправленный шифр, также придуманный Деластелем, был первым шифром для реализации принципов путаницы и распространения. Как отмечал сам Деластель, он наиболее практичен для шифрования латинского алфавита, лежащего в основе большинства европейских языков, поскольку в латинском алфавите 26 букв, а трёхраздельный шифр использует 27 позиций для шифрования.

Итак, перейдём к задаче.

Пример шифрования

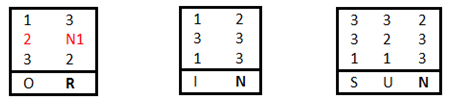
Даны три ключевых таблицы:

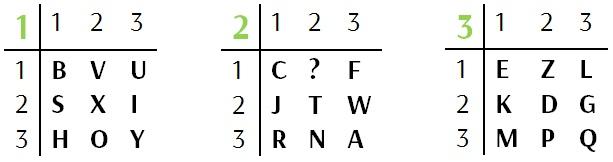
Зашифруем слово TOPSECRET.

Находим букву Т в таблице 2, столбце 2, строке 2. Записываем три цифры вертикально друг под другом. Теперь ищем букву О в таблицах. Получаем следующие координаты {1 2 3} и записываем их. Так же продолжаем для всех оставшихся букв, а результаты записываем столбиком слева направо.

Шифрование работает следующим образом. Первая горизонтальная группа из трёх букв — {2 1 3}. Выписываем букву из третьей строки первого столбца второй таблицы — R. Следующая триграмма — {1 3 2}, по этим координатам находится буква I. Таким образом используем все триграммы и получаем зашифрованный текст RIWTBSACK.

Для удобства расшифровки запишем шифрованное сообщение вертикально и выпишем по порядку координаты каждой буквы (номер таблицы, номер столбца, ном

Полученные числовые тройки выпишем горизонтально слева направо таким образом, чтобы в каждой строке было одинаковое количество цифр.

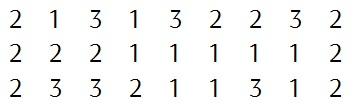
Далее уже по столбцам слева направо берём координаты, выписываем буквы из ключевых таблиц и получаем исходное сообщение.

Обратите внимание, что необязательно заканчивать ряд сразу после триграммы, она вполне может разбиваться и переноситься на следующую строку. Главный принцип заключается в одинаковом количестве символов в строках.

Задача

Два английских профессора на пенсии Многочей и Малобол посылают друг другу сообщения, зашифрованные с помощью трёхраздельного шифра. Ранее они обменялись ключом, состоящим из трёх таблиц. Профессор Малобол получает зашифрованный текст от своего коллеги Многочея, но по исключительной рассеянности профессор Малобол потерял вторую таблицу ключа. Сможет ли профессор восстановить открытый текст, несмотря на недостаточность ключевой информации?

Профессору необходима помощь с дешифрованием сообщения.

Для решения задачи необходимо:

1. Найти девять пропущенных букв латинского алфавита второй таблицы и расставить их в правильном порядке.

2. Сформировать числовые триграммы и записать правильные буквы открытого текста.

Зашифрованный текст

EMKE MEWAM OF YTDDC GFTY LYEWIG

KM ZHEPITO ?OVGG?NS? IJ EB JGUUG

EEVU NBQ WNPTYFDUOYY VKLR

EEWE MXO LLSHSTN XVYF TYL FXG

WWEV EMBR FZ AVT MUZ AAV EH LIJ

EDWBM OTW YFEYPZ

FEEK ESL IJFLA

EDKEK BE TMZV NIYF KBEAYGH

Зашифрованный текст соответствует английским словам, то есть пробел в зашифрованном тексте находится в той же позиции, что и пробел в открытом тексте. Открытый текст был зашифрован построчно, при этом сначала все пробелы были удалены до процесса шифрования и вставлены на те же самые места в уже зашифрованный текст.

Решение

Так как буквы в таблицах используются один раз, найдём буквы, из которых состоит вторая таблица простым исключением из алфавита:

Получим следующие буквы: BEHLMNTVW.

Далее разобьём шифрованное сообщение на трёхбуквенные группы и распишем координаты букв в таблице, при этом координаты букв второй таблицы обозначим через литеру и цифру (например, Е = {2 Е1 Е2}).

Красным отмечены буквы из второй таблицы. В этой таблице использованы только буквы для координат, чтобы её не загромождать. Далее будут использоваться и цифры.

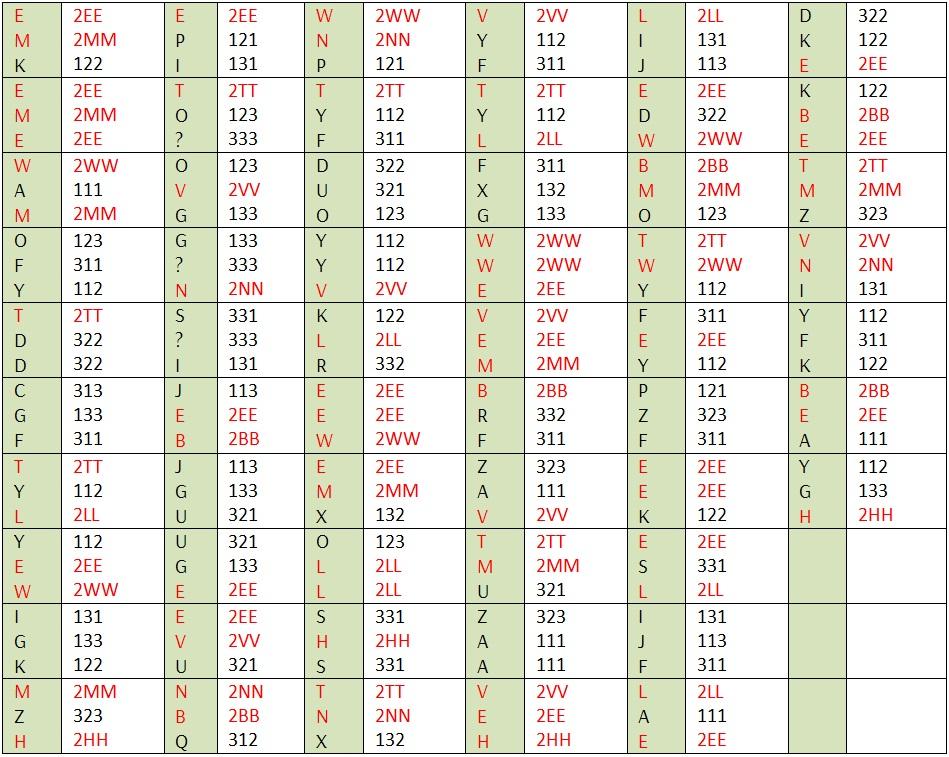
Полученные цифры запишем в табличной форме построчно слева направо для каждой строки отдельно и внесём в полученные таблицы известные по координатам буквы. Получилось не так уж и много.

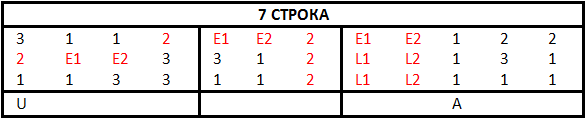
Перейдём к анализу. Начнём с самых коротких слов. Обратите внимание на вторую строку. Здесь у нас два двухбуквенных слова. {1 2 3} — это буква O, а {3 N1 2}, скорее всего, — буква R, и, соответственно, слово — это союз OR. Значит, координата N1 = 3. Учитывая первое слово в этой же строке, предположим, что это предлог IN и вторая координата N2 = 3. Расставим полученные координаты N = {2 3 3} по остальным строкам для подтверждения этой гипотезы. Действительно, получаем два предлога IN во второй строке, союз AND в четвёртой, популярное окончание -ING в третьем слове второй строки и восьмое слово в пятой строке SUN. Расставим N в соответствующие координатам {2 3 3} места.

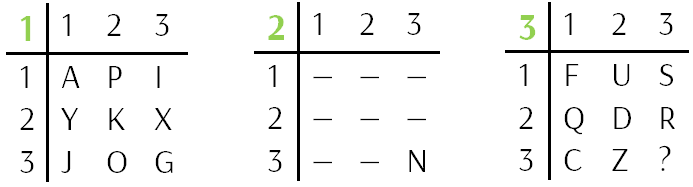
В данной системе шифрования имеется одна интересная особенность, которая играет нам на руку. Для шифрования используются три таблицы по девять членов в каждой, однако в английском алфавите всего 26 букв, поэтому 27 символом стал знак вопроса с координатами {3 3 3}. Учитывая эту особенность, проанализируем получившиеся таблицы.

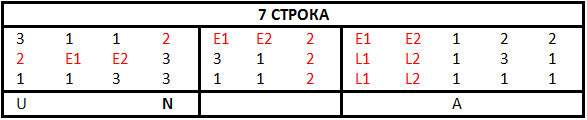
Так как знак вопроса не может находиться внутри слова, получается, что M2 ≠ 3 (2 слово 2 строка), E1 ≠ 3 (1 слово 6 строка), E2 ≠ 3 (3 слово 3 строка). Также, скорее всего, T1 ≠ T2 (2 слово 6 строка), поскольку вероятность наличия в тексте трёхбуквенного слова с двумя первыми одинаковыми буквами очень мала (да и не знаю я такого слова).

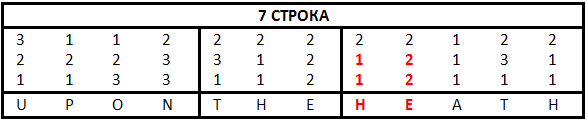
Пока более всего в текущем зашифрованном тексте привлекают внимание четыре слова: 6 в первой строке, 6 во второй, 4 в третьей и 1 в седьмой. Рассмотрим возможные сочетания букв в этих словах.

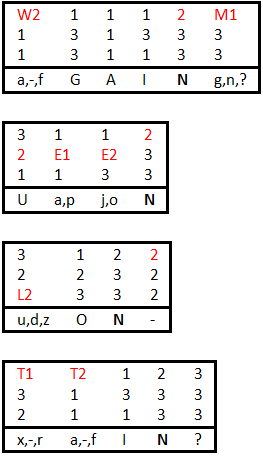
Итак, простым перебором вычисляем, что 6 слово первой строки, скорее всего, AGAIN? Первая буква — точно не F из третьей таблицы. Оставшиеся буквы второй таблицы не подходят, поэтому выбираем букву A. В окончании слова не может быть G и N, значит это знак вопроса из третьей таблицы. Таким образом, M1 = 3, W2 = 1.

Также перебором вычисляем первое слово седьмой строки: UPON. Значит E1 = 2, E2 = 2.

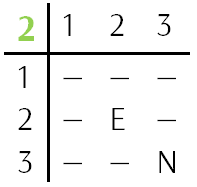
Для проверки гипотез просмотрим весь текст. Сразу бросаются в глаза:

Зная координаты букв E = {2 2 2} и частотность слов в английском языке, предположим, что это определённый артикль — THE.

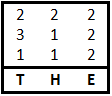
Таким образом, у нас появились новые данные T1 = 3, T2 = 1, W1 = 2, H1 = 1, H2 = 1, и подтвердились координаты E. Занесём полученные результаты во вторую ключевую таблицу и зашифрованные строки.

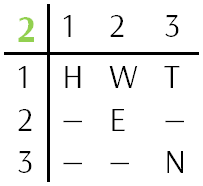
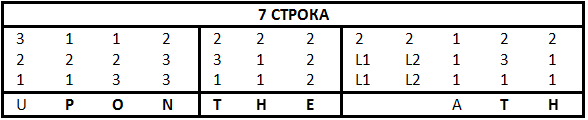
Привлекают внимание 1 слово 1 строки, 1 слово 3 строки и 1 слово 4 строки:

Учитывая все имеющиеся данные, получаем M2 = 2, L1 = 1 и L2 = 2.

Таким образом:

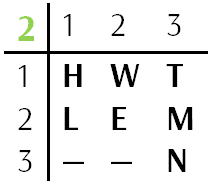
У нас осталось всего две буквы: B и V.

Воспользуемся простой подстановкой. Разместим B по координатам {2 1 3}, а V — {2 2 3}, а потом поменяем их местами, если не получится.

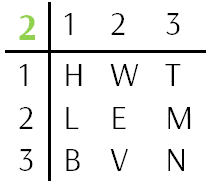
В итоге получилось, что верным был первый вариант, и мы получили расшифрованный текст, оказавшийся диалогом трёх ведьм в первой сцене первого акта одной из самых известных трагедий Уильяма Шекспира «Макбет»:

When shall we three meet again?

In thunder, lightning, or in rain?

When the hurly-burly's done,

When the battle's lost and won.

That will be ere the set of sun.

Where the place?

Upon the heath.

There to meet with Macbeth.

Когда средь молний, в дождь и гром

Мы вновь увидимся втроем?

Когда один из воевод

Другого в битве разобьет.

Заря решит ее исход.

Где нам сойтись?

На пустыре.

Макбет там будет к той поре.

(перевод Б. Пастернак)

Использованный в задаче трёхраздельный шифр Деластеля является классическим полиграфическим подстановочным шифром. В замечательной книге Дэвида Кана («Взломщики кодов») упоминается, что шифры, разработанные Деластелем, сыграли значительную роль в развитии криптографической науки. Сейчас понятно, что эти шифры ненадёжны и тяготеют к частотному анализу, несмотря на принятые меры по усложнению, однако довольно долго после своего появления этот и подобные ему шифры вполне себе служили по своему профилю.

НЛО прилетело и оставило здесь промокод для читателей нашего блога:
— 15% на заказ любого VDS (кроме тарифа Прогрев) — HABRFIRSTVDS