Русский математик Андрей Андреевич Марков без сомнения известен всем любителям математики, как создатель т.н. "цепей Маркова" - последовательности случайных событий, где вероятность наступления каждого события зависит только от состояния, достигнутого в предыдущем событии.

Однако сегодня мы поговорим о его менее известном открытии, связанном с исследованием решений в целых числах следующего диофантова уравнения:

Решений уравнения Маркова - бесконечное количество, и все они получаются по очень простой формуле (впрочем, вывод её достаточно объемный - смотреть здесь на с. 31). В её основе лежит первое приходящее на ум тривиальное решение:

Тогда остальные решения выводятся по формуле:

В результате чего перестановкой получаются следующие тройки чисел:

Каноничной из них считается та, в которой числа упорядочены по возрастанию, т.е. последняя, которая и называется марковской тройкой. Теперь фиксируем первое значение и вычисляем следующую тройку:

Дальше есть два пути (забегая вперед, в остальных марковских тройках нет повторяющихся значений). В первом случае мы меняем местами q и r, во втором - p и r. Схематично вычисление выглядит так:

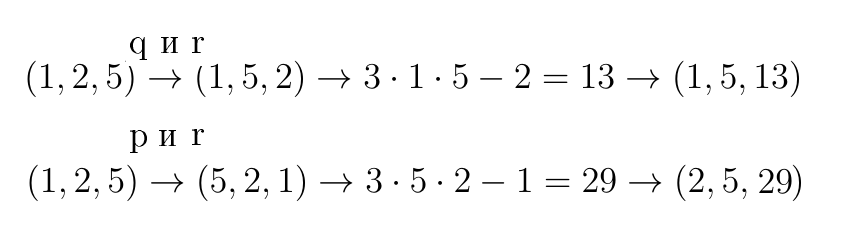
Все возможные марковские тройки, как Вы могли догадаться, целиком и полностью состоят из марковских чисел. Первые из них (всего их бесконечное количество):

Если продолжать процесс ветвления для каждой марковской тройки, получим дерево:

Обратите внимание на выделенные красным цветом числа - это нечетные члены последовательности Фибоначчи! Выделенные зеленым цветом - т.н. числа Пелля, получаемые при решении одноименного уравнения.

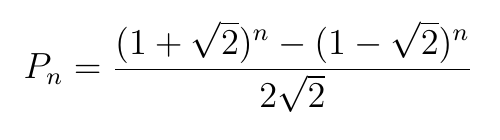
Наивно думать, что Марков в теории чисел изучал всего лишь одно конкретное уравнение. Наоборот, его числа родились во время исследования целой математической области - т.н. квадратичных форм, где Марков выделил специальные формы (второй столбец):

Если попытаться вычислить значение последней дроби, оно будет равным примерно 2.9999. Марков показал, что эта величина стремится к 3. Прелюдия закончена. Начинается математическая магия.

Приближения иррациональных чисел

Удивительно, но числа Маркова проявляются в теории приближения иррациональных чисел рациональными дробями:

Это утверждение означает, что всякое иррациональное число α можно приблизить рациональной дробью p/q с требуемой точностью, которая зависит только от знаменателя q. Например:

Т.е., выбирая q=10 мы получили приближение с погрешностью меньше 5 %, а наилучшее приближение числа π в данном случае - это дробь 31/10. А что будет если взять другие значения q? Оказывается, прямой зависимости в уменьшении погрешности нет:

Т.е. наметившееся уменьшение погрешности в дребезги разбивается, например, при q=125, где наилучшее приближение хуже, чем при меньших значениях знаменателя. Напрашивается вывод, что не все q подходят для того, что наилучшим образом приближать иррациональные числа, да и вообще в правой части может быть не такое простое выражение.

Немецкий математик Адольф Гурвиц показал, что некоторые иррациональные числа можно приближать точнее и точнее, если использовать в качестве дроби справа следующие выражения:

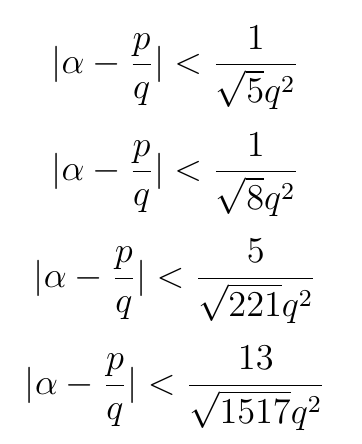
В 1921 году математик Оскар Перрон нашел ключ, который наконец связал числа Маркова с коэффициентами наилучшего приближения иррациональных чисел:

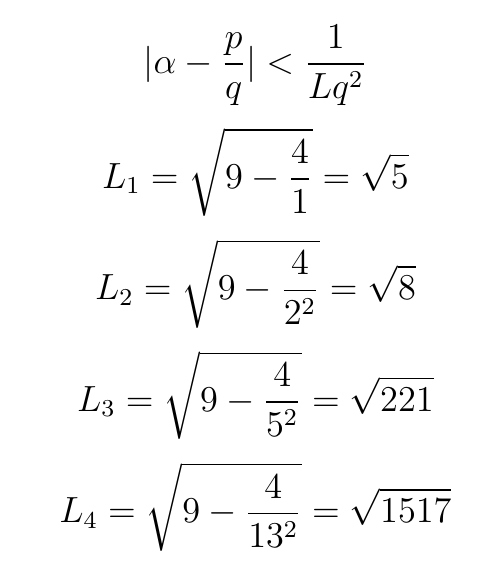
Как видите, числа Маркова являются собой замечательную, скрытую от невооруженного глаза, связь непрерывного (квадратичных форм) и дискретного (рациональных приближений). Этим и прекрасна математика!

Подборка материалов по числам Маркова:

• Теорема Маркова и гипотеза единственности (объемная книга, целиком посвященная проблематике) / англ.

• Оригинал работы Маркова по теории квадратичных форм / англ.

• Отдельная статья про гипотезу единственности (утверждает, что каждое число Маркова является наибольшим в тройке только один раз) / англ.

• О геодезических (кратчайших) линиях и их связи с числами Маркова / англ.

• Связь целочисленной геометрии и чисел Маркова / англ.

• Спектры Маркова и Лагранжа (по сути некоторые наборы для квадратичных форм с определенным дискриминантом) / англ.

• О распределении чисел Маркова / англ.

• О сопоставлении дерева Маркова с двоичными словами специального вида / англ.

• Объяснение, почему уравнение Маркова с правой частью вида n*pqr при n>3 не имеет решения / англ.

• Введение в теорию диофантовых приближений / рус.

• Комбинаторика марковских чисел / англ.

  Всё это и много другое, заботливо упакованное в один архив, - "Математика не для всех"

Эта статья поддерживается командой ITGLOBAL.COM

Мы — первый облачный провайдер в России, а также интегратор, поставщик ИТ-услуг, продуктов, сервисов и разработчик собственного ПО.  

•  Наш сайт
•  Наш блог про виртуализацию и Enterprise IT
•  Наш YouTube канал
•  Истории успеха наших клиентов