На днях завершился очередной чемпионат мира по хоккею.
За просмотром матчей родилась идея. Когда в перерывах телевизионная камера показывает уходящих в раздевалку игроков, трудно не заметить, насколько они огромные. На фоне тренеров, функционеров команд, сотрудников ледовой арены, журналистов или просто фанатов они, как правило, выглядят очень внушительно.
И я задался вопросами. Действительно ли хоккеисты выше обычных людей? Как изменяется рост хоккеистов со временем в сравнении с обычными людьми? Есть ли устойчивые межстрановые различия?
Данные
IIHF, организация, проводящая чемпионаты мира по хоккею, каждый год публикует составы участвующих команд с информацией о росте и весе каждого игрока. Архив этих данных тут.
Я собрал вместе данные всех чемпионатов мира с 2001 по 2016 годы. От года к году формат предоставления данных слегка меняется, что требует некоторых усилий по их очистке. Не представляя, как грамотно автоматизировать процесс, все данные копировал вручную, что заняло чуть больше 3 часов. Объединенный датасет выложил в открытый доступ.
# load required packages
require(dplyr) # data manipulation
require(lubridate) # easy manipulations with dates
require(ggplot2) # visualization
require(ggthemes) # themes for ggplot2
require(cowplot) # nice alignment of the ggplots
require(RColorBrewer) # generate color palettes
require(texreg) # easy export of regression tables
require(xtable) # export a data frame into an html table
# download the IIHF data set; if there are some problems, you can download manually
# using the stable URL (https://dx.doi.org/10.6084/m9.figshare.3394735.v2)
df <- read.csv('https://ndownloader.figshare.com/files/5303173')
# color palette
brbg11 <- brewer.pal(11,'BrBG')Растут ли хоккеисты? Грубое (периодное) сравнение
Для начала сравним средний рост игроков на всех 16 чемпионатах мира.

# mean height by championship
df_per <- df %>% group_by(year) %>%
summarise(height=mean(height))
gg_period_mean <- ggplot(df_per, aes(x=year,y=height))+
geom_point(size=3,color=brbg11[9])+
stat_smooth(method='lm',size=1,color=brbg11[11])+
ylab('height, cm')+
xlab('year of competition')+
scale_x_continuous(breaks=seq(2005,2015,5),labels=seq(2005,2015,5))+
theme_few(base_size = 15)+
theme(panel.grid=element_line(colour = 'grey75',size=.25))
gg_period_jitter <- ggplot(df, aes(x=year,y=height))+
geom_jitter(size=2,color=brbg11[9],alpha=.25,width = .75)+
stat_smooth(method='lm',size=1,se=F,color=brbg11[11])+
ylab('height, cm')+
xlab('year of competition')+
scale_x_continuous(breaks=seq(2005,2015,5),labels=seq(2005,2015,5))+
theme_few(base_size = 15)+
theme(panel.grid=element_line(colour = 'grey75',size=.25))
gg_period <- plot_grid(gg_period_mean,gg_period_jitter)Положительный тренд очевиден. За полтора десятилетия средний рост хоккеиста на чемпионате мира увеличился почти на 2 сантиметра (левая панель). Как будто бы незначительный прирост на фоне довольно большой вариации (правая панель). Много это или мало? Чтобы ответить на вопрос, надо корректно сравнить с населением (но об этом ближе к концу статьи).
Когортный анализ
Более корректный способ изучения изменения в росте подразумевает сравнение по когортам рождения. Тут мы сталкиваемся с любопытным нюансом — некоторые хоккеисты участвовали не в одном чемпионате мира. Вопрос: вычищать ли повторные записи для одних и тех же людей? Если нам интересен средний рост хоккеиста на чемпионате (как на картинке выше), пожалуй, не имеет смысла зачищать. Но если мы хотим проследить изменение роста хоккеистов как таковое, на мой взгляд, было бы неправильно присваивать больший вес тем игрокам, которые регулярнее попадали на чемпионаты мира. Поэтому для дальнейшего анализа я очистил данные от повторных записей одних и тех же игроков.
# remove double counts
dfu_h <- df %>% select(year,name,country,position,birth,cohort,height) %>%
spread(year,height)
dfu_h$av.height <- apply(dfu_h[,6:21],1,mean,na.rm=T)
dfu_h$times_participated <- apply(!is.na(dfu_h[,6:21]),1,sum)
dfu_w <- df %>% select(year,name,country,position,birth,cohort,weight) %>%
spread(year,weight)
dfu_w$av.weight <- apply(dfu_w[,6:21],1,mean,na.rm=T)
dfu <- left_join(dfu_h %>% select(name,country,position,birth,cohort,av.height,times_participated),
dfu_w %>% select(name,country,position,birth,cohort,av.weight),
by = c('name','country','position','birth','cohort')) %>%
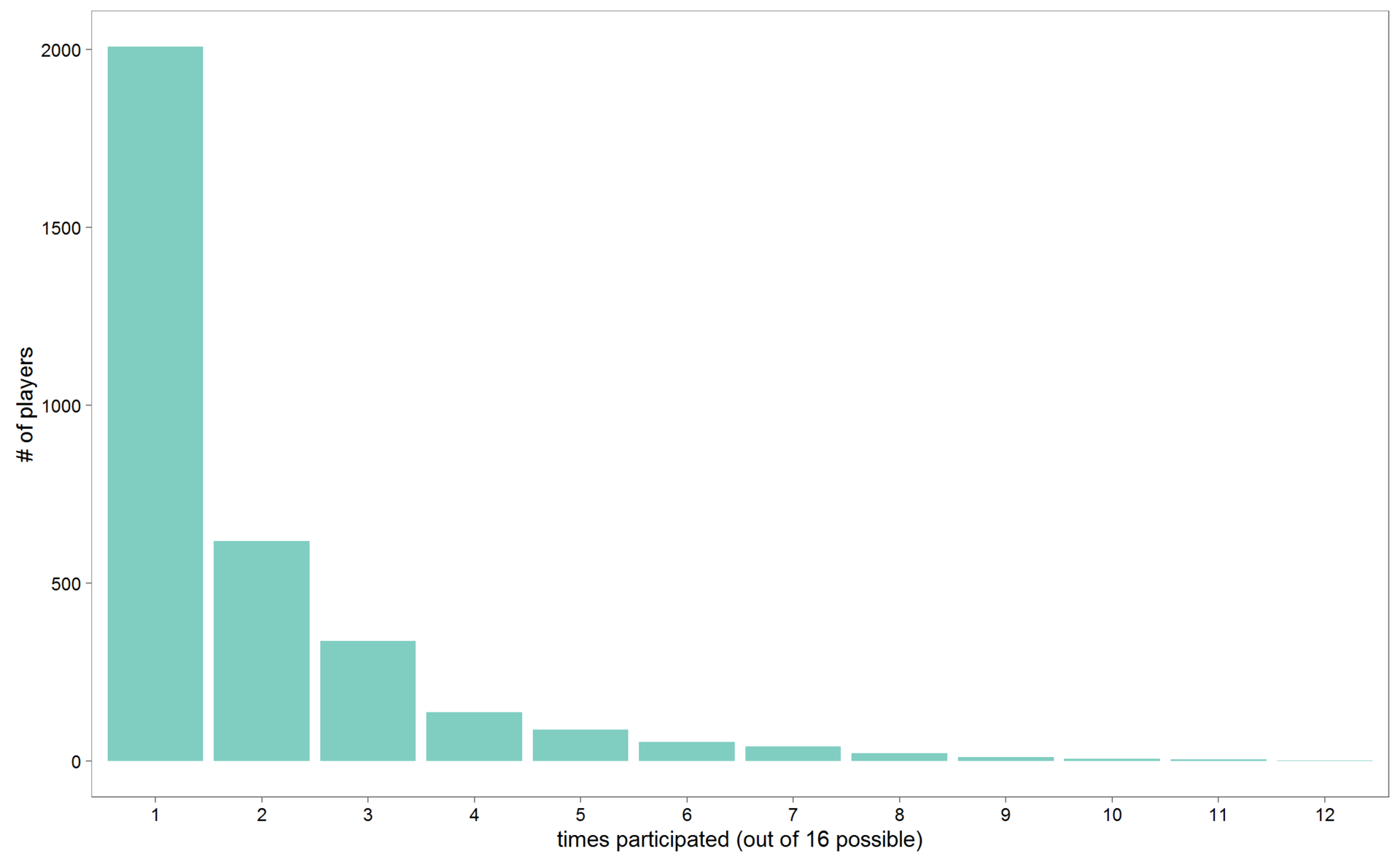
mutate(bmi = av.weight/(av.height/100)^2)Общее количество наблюдений сократилось с 6292 до 3333. Если хоккеист участвовал более чем в одном чемпионате мира, данные о росте и весе я усреднял, поскольку рост и (в особенности) вес отдельно взятого хоккеиста мог меняться со временем. Сколько же раз хоккеисты удостаиваются чести сыграть за национальные сборные на чемпионатах мира? В среднем чуть менее 2 раз.
# frequencies of participation in world championships
mean(dfu$times_participated)
df_part <- as.data.frame(table(dfu$times_participated))
gg_times_part <- ggplot(df_part,aes(y=Freq,x=Var1))+
geom_bar(stat='identity',fill=brbg11[9])+
ylab('# of players')+
xlab('times participated (out of 16 possible)')+
theme_few(base_size = 15)Но есть и уникумы. Посмотрим, кто из игроков принял участие как минимум в 10 чемпионатах мира. Таких игроков оказалось 14.
# the leaders of participation in world championships
# save the table to html
leaders <- dfu %>% filter(times_participated > 9)
View(leaders)
print(xtable(leaders), type="html", file="table_leaders.html")| name | country | position | birth | cohort | av.height | times_participated | av.weight | bmi | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | ovechkin alexander | RUS | F | 1985-09-17 | 1985 | 188.45 | 11 | 98.36 | 27.70 |
| 2 | nielsen daniel | DEN | D | 1980-10-31 | 1980 | 182.27 | 11 | 79.73 | 24.00 |
| 3 | staal kim | DEN | F | 1978-03-10 | 1978 | 182.00 | 10 | 87.80 | 26.51 |
| 4 | green morten | DEN | F | 1981-03-19 | 1981 | 183.00 | 12 | 85.83 | 25.63 |
| 5 | masalskis edgars | LAT | G | 1980-03-31 | 1980 | 176.00 | 12 | 79.17 | 25.56 |
| 6 | ambuhl andres | SUI | F | 1983-09-14 | 1983 | 176.80 | 10 | 83.70 | 26.78 |
| 7 | granak dominik | SVK | D | 1983-06-11 | 1983 | 182.00 | 10 | 79.50 | 24.00 |
| 8 | madsen morten | DEN | F | 1987-01-16 | 1987 | 189.82 | 11 | 86.00 | 23.87 |
| 9 | redlihs mikelis | LAT | F | 1984-07-01 | 1984 | 180.00 | 10 | 80.40 | 24.81 |
| 10 | cipulis martins | LAT | F | 1980-11-29 | 1980 | 180.70 | 10 | 82.10 | 25.14 |
| 11 | holos jonas | NOR | D | 1987-08-27 | 1987 | 180.18 | 11 | 91.36 | 28.14 |
| 12 | bastiansen anders | NOR | F | 1980-10-31 | 1980 | 190.00 | 11 | 93.64 | 25.94 |
| 13 | ask morten | NOR | F | 1980-05-14 | 1980 | 185.00 | 10 | 88.30 | 25.80 |
| 14 | forsberg kristian | NOR | F | 1986-05-05 | 1986 | 184.50 | 10 | 87.50 | 25.70 |
Александр Овечкин, 11 раз! Но тут надо отметить, что не для всех хоккеистов в принципе возможно было поучаствовать во всех 16 чемпионатах: зависит когорты рождения (насколько игровая карьера пересеклась именно с этим периодом наблюдения), от того, участвовала ли сборная игрока во всех чемпионатах мира (см. рисунок 3) и попадал ли игрок стабильно в сборную; наконец есть еще НХЛ, стабильно отвлекающий лучших из лучших от участия в чемпионатах мира.

# countries times participated
df_cnt_part <- df %>% select(year,country,no) %>%
mutate(country=factor(paste(country))) %>%
group_by(country,year) %>%
summarise(value=sum(as.numeric(no))) %>%
mutate(value=1) %>%
ungroup() %>%
mutate(country=factor(country, levels = rev(levels(country))),
year=factor(year))
d_cnt_n <- df_cnt_part %>% group_by(country) %>%
summarise(n=sum(value))
gg_cnt_part <- ggplot(data = df_cnt_part, aes(x=year,y=country))+
geom_point(color=brbg11[11],size=7)+
geom_text(data=d_cnt_n,aes(y=country,x=17.5,label=n,color=n),size=7,fontface=2)+
geom_text(data=d_cnt_n,aes(y=country,x=18.5,label=' '),size=7)+
scale_color_gradientn(colours = brbg11[7:11])+
xlab(NULL)+
ylab(NULL)+
theme_bw(base_size = 25)+
theme(legend.position='none',
axis.text.x = element_text(angle = 90, hjust = 1,vjust=0.5))Растут ли хоккеисты? Регрессионный анализ
Регрессионный анализ позволяет более корректно ответить на вопрос об изменении роста игроков. В данном случаем с помощью мультиноминальной линейной регрессии предсказыватся рост хоккеиста в зависимость от когорты рождения. Включая в спецификацию регресиионной модели различные дополнительные (контрольные) переменные, мы получаем значение наиболее интересующего нас коэффициента "при прочих равных". Например, добавляя к объясняющим переменным помимо когорты рождения позицию игрока на поле, мы получаем взаимосвязь роста и когорты, очищенную от эффекта различий в зависимости от позиции; добавляя в контрольны переменные страны, получаем результат, очищенный от межстрановых различий. Разумеется, если контрольные переменные сами оказываются значимыми, на это тоже стоит обратить внимание.
Регрессионные модели (особенно линейные регрессии) очень чувствительны к выбросам (см., например, эту статью). Не вдаваясь глубоко в эту обширную тему, я лишь убрал из анализа когорты, для которых мы имеем слишком небольшое количество представителей.
# remove small cohorts
table(dfu$cohort)
dfuc <- dfu %>% filter(cohort<1997,cohort>1963)Не желая резать данные сильно, я убрал только когорты 1963, 1997 и 1998 годов рождения, для которых у нас есть менее 10 игроков.
Итак, результаты рагрессионного анализа. В каждой следующей модели я добавляю одну переменную.
Зависимая переменная: рост хоккеиста.
Объясняющие перемеенные: 1) когорта рождения; 2) + позиция на поле (сравнение с защитниками); 3) + страна (сравнение с Россией).
# relevel counrty variable to compare with Russia
dfuc$country <- relevel(dfuc$country,ref = 'RUS')
# regression models
m1 <- lm(data = dfuc,av.height~cohort)
m2 <- lm(data = dfuc,av.height~cohort+position)
m3 <- lm(data = dfuc,av.height~cohort+position+country)
# export the models to html
htmlreg(list(m1,m2,m3),file = 'models_height.html',single.row = T)| Model 1 | Model 2 | Model 3 | ||
|---|---|---|---|---|
| (Intercept) | -10.17 (27.67) | -18.64 (27.01) | 32.59 (27.00) | |
| cohort | 0.10 (0.01)*** | 0.10 (0.01)*** | 0.08 (0.01)*** | |
| positionF | -2.59 (0.20)*** | -2.59 (0.20)*** | ||
| positionG | -1.96 (0.31)*** | -1.93 (0.30)*** | ||
| countryAUT | -0.94 (0.55) | |||
| countryBLR | -0.95 (0.53) | |||
| countryCAN | 1.13 (0.46)* | |||
| countryCZE | 0.56 (0.49) | |||
| countryDEN | -0.10 (0.56) | |||
| countryFIN | 0.20 (0.50) | |||
| countryFRA | -2.19 (0.69)** | |||
| countryGER | -0.61 (0.51) | |||
| countryHUN | -0.61 (0.86) | |||
| countryITA | -3.58 (0.61)*** | |||
| countryJPN | -5.24 (0.71)*** | |||
| countryKAZ | -1.16 (0.57)* | |||
| countryLAT | -1.38 (0.55)* | |||
| countryNOR | -1.61 (0.62)** | |||
| countryPOL | 0.06 (1.12) | |||
| countrySLO | -1.55 (0.58)** | |||
| countrySUI | -1.80 (0.53)*** | |||
| countrySVK | 1.44 (0.50)** | |||
| countrySWE | 1.18 (0.48)* | |||
| countryUKR | -1.82 (0.59)** | |||
| countryUSA | 0.54 (0.45) | |||
| R2 | 0.01 | 0.06 | 0.13 | |
| Adj. R2 | 0.01 | 0.06 | 0.12 | |
| Num. obs. | 3319 | 3319 | 3319 | |
| RMSE | 5.40 | 5.27 | 5.10 | |
| ***p < 0.001, **p < 0.01, *p < 0.05 | ||||
Интерпретация моделей
Модель 1. Увеличение когорты на один год соответсвует увеличению роста хоккеистов на 0.1 см. Коэффициент статистически значим, но при этом модель объясняет лишь 1% вариации зависимой переменной. В принципе это не проблема, поскольку моделирование носит объясняющий характер, задача предсказания не ставится. Тем не менее, низкий коэффициент детерминации показывает, что должны быть другие переменные, гораздо лучше объясняющие различия между хоккеистами в росте.
Модель 2. Защитники — самые высокие игроки в хоккее. Вратари ниже на 2 см, нападающие — на 2.6 см. Все коэффициенты статистически значимы. Объясненная вариация зависимой переменной возрастает до 6%. При этом коэффициент при переменной когорта рождения не изменяется.
Модель 3. Добавление контрольных переменных для стран любопытно по двум причинам. Во-первых, некоторые различия статистически значимы и интересны сами по себе. Так, например, шведы, словаки и канадцы статистически значимо выше наших игроков. Большинство же наций значительно ниже нас, японцы аж на 5.2 см, итальянцы — на 3.6 см, французы — на 2.2 см (см. также рисунок 4). Во-вторых, введение контрольных переменных для стран значительно уменьшает коэффициент при переменной когорта рождения — до 0.08. Это значит, что межстрановые различия объясняют часть различий по когортам рождения. Коэффициент детерминации модели возрастает до 13%.

# players' height by country
gg_av.h_country <- ggplot(dfuc ,aes(x=factor(cohort),y=av.height))+
geom_point(color='grey50',alpha=.25)+
stat_summary(aes(group=country),geom='line',fun.y = mean,size=.5,color='grey50')+
stat_smooth(aes(group=country,color=country),geom='line',size=1)+
#geom_hline(yintercept = mean(height),color='red',size=.5)+
facet_wrap(~country,ncol=4)+
coord_cartesian(ylim = c(170,195))+
scale_x_discrete(labels=paste(seq(1965,1995,10)),breaks=paste(seq(1965,1995,10)))+
theme_few(base_size = 15)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))Наиболее полная модель показывает, что увеличение роста хоккеистов происходит со скоростью 0.08 см в год. Это означает прирост 0.8 см за десятилетие или на 2.56 см за 32 года с 1964 по 1996. Обратите внимание, что при учете контрольных переменных скорость увеличения роста хоккеистов оказывается примерно в полтора раза ниже, чем при более грубом анализе средних значений (рисунок 1): 0.8 см за десятилетие против примерно 1.2 см.
Прежде чем мы, наконец, постараемся понять, насколько значительным оказывается увеличение роста, хочу обратить внимание еще на один любопытный момент. Введение контрольных переменных подразумевает фиксацию различий между категориями при едином наклоне регрессионной линии (единый коэффициент при главной объясняющей переменной). Это не всегда хорошо и может замаскировать значительные различия в тесноте связи между исследуемыми переменными в подвыборках. Так, например, раздельное моделирование зависимости роста игроков от амплуа (рисунок 5) показывает, что взаимосвязь наиболее ярко выражена для вратарей и наименее заметна для защитников.

dfuc_pos <- dfuc
levels(dfuc_pos$position) <- c('Defenders','Forwards','Goalkeeprs')
gg_pos <- ggplot(dfuc_pos ,aes(x=cohort,y=av.height))+
geom_jitter(aes(color=position),alpha=.5)+
stat_smooth(method = 'lm', se = T,color=brbg11[11],size=1)+
scale_x_continuous(labels=seq(1965,1995,5),breaks=seq(1965,1995,5))+
scale_color_manual(values = brbg11[c(8,4,10)])+
facet_wrap(~position,ncol=3)+
xlab('birth cohort')+
ylab('height, cm')+
theme_few(base_size = 20)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))# separate models for positions
m3d <- lm(data = dfuc %>% filter(position=='D'),av.height~cohort+country)
m3f <- lm(data = dfuc %>% filter(position=='F'),av.height~cohort+country)
m3g <- lm(data = dfuc %>% filter(position=='G'),av.height~cohort+country)
htmlreg(list(m3d,m3f,m3g),file = '2016/160500 Hockey players/models_height_pos.html',single.row = T,
custom.model.names = c('Model 3 D','Model 3 F','Model 3 G'))| Model 3 D | Model 3 F | Model 3 G | ||
|---|---|---|---|---|
| (Intercept) | 108.45 (46.46)* | 49.32 (36.73) | -295.76 (74.61)*** | |
| cohort | 0.04 (0.02) | 0.07 (0.02)*** | 0.24 (0.04)*** | |
| countryAUT | 0.14 (0.96) | -2.01 (0.75)** | 0.47 (1.47) | |
| countryBLR | 0.30 (0.87) | -1.53 (0.73)* | -2.73 (1.55) | |
| countryCAN | 1.55 (0.78)* | 0.39 (0.62) | 3.45 (1.26)** | |
| countryCZE | 0.87 (0.84) | 0.30 (0.67) | 0.63 (1.36) | |
| countryDEN | -0.60 (0.95) | 0.10 (0.75) | -0.19 (1.62) | |
| countryFIN | -0.55 (0.89) | -0.04 (0.67) | 2.40 (1.32) | |
| countryFRA | -3.34 (1.15)** | -2.06 (0.93)* | 1.39 (2.07) | |
| countryGER | 0.48 (0.85) | -1.40 (0.72) | -0.65 (1.33) | |
| countryHUN | -1.32 (1.47) | -0.70 (1.16) | 0.65 (2.39) | |
| countryITA | -2.08 (1.08) | -4.78 (0.82)*** | -2.02 (1.62) | |
| countryJPN | -4.13 (1.26)** | -6.52 (0.94)*** | -2.27 (1.98) | |
| countryKAZ | -1.23 (0.95) | -1.82 (0.79)* | 1.79 (1.58) | |
| countryLAT | -0.73 (0.95) | -1.39 (0.75) | -3.42 (1.49)* | |
| countryNOR | -3.25 (1.07)** | -1.06 (0.85) | -0.10 (1.66) | |
| countryPOL | 0.82 (1.89) | -0.58 (1.55) | 0.37 (2.97) | |
| countrySLO | -1.57 (0.99) | -1.54 (0.79) | -2.25 (1.66) | |
| countrySUI | -1.98 (0.91)* | -2.36 (0.71)*** | 1.12 (1.47) | |
| countrySVK | 2.94 (0.87)*** | 0.81 (0.67) | -0.70 (1.50) | |
| countrySWE | 0.75 (0.81) | 1.24 (0.65) | 1.37 (1.33) | |
| countryUKR | -1.37 (1.01) | -1.77 (0.80)* | -3.71 (1.66)* | |
| countryUSA | 0.76 (0.78) | -0.08 (0.62) | 2.58 (1.26)* | |
| R2 | 0.09 | 0.10 | 0.24 | |
| Adj. R2 | 0.07 | 0.09 | 0.20 | |
| Num. obs. | 1094 | 1824 | 401 | |
| RMSE | 5.08 | 5.08 | 4.87 | |
| ***p < 0.001, **p < 0.01, *p < 0.05 | ||||
Раздельное моделирование показывает, что в когортах 1964-1996 годов рождения, средний рост хоккеистов, участвовавших в чемпионатах мира в 2001-2016 годах, увеличивался со скоростью 0.4 см за десятиление для защитников, 0.7 см — для нападающих и (!) 2.4 см — для вратарей. За три десятиления средний рост вратарей увеличился на 7 см!
Пришло время сравнить эти изменения со средними значениями для населения.
Сравнение с населением
Результаты регрессионного анализа фиксируют значительные межстрановые различия. Поэтому сравнивать имеет смысл по странам: хоккеистов определенной страны с мужским населением этой же страны.
Для сравнения роста хоккеистов со средними показателями мужского населения я использовал данные из релевантной научной статьи (PDF). Данные я скопировал из статьи (использовав замечательную программку tabula) и тоже разместил в открытом доступе.
# download the data from Hatton, T. J., & Bray, B. E. (2010).
# Long run trends in the heights of European men, 19th–20th centuries.
# Economics & Human Biology, 8(3), 405–413.
# http://doi.org/10.1016/j.ehb.2010.03.001
# stable URL, copied data (https://dx.doi.org/10.6084/m9.figshare.3394795.v1)
df_hb <- read.csv('https://ndownloader.figshare.com/files/5303878')
df_hb <- df_hb %>%
gather('country','h_pop',2:16) %>%
mutate(period=paste(period)) %>%
separate(period,c('t1','t2'),sep = '/')%>%
transmute(cohort=(as.numeric(t1)+as.numeric(t2))/2,country,h_pop)
# calculate hockey players' cohort height averages for each country
df_hoc <- dfu %>% group_by(country,cohort) %>%
summarise(h_hp=mean(av.height)) %>%
ungroup()К сожалению, данные о динамике роста населения пересекаются лишь с 8 странами из моего хоккейного датасета: Австрия, Дания, Финляндия, Франция, Германия, Италия, Норвегия, Швеция.
# countries in both data sets
both_cnt <- levels(factor(df_hb$country))[which(levels(factor(df_hb$country)) %in% levels(df_hoc$country))]
both_cnt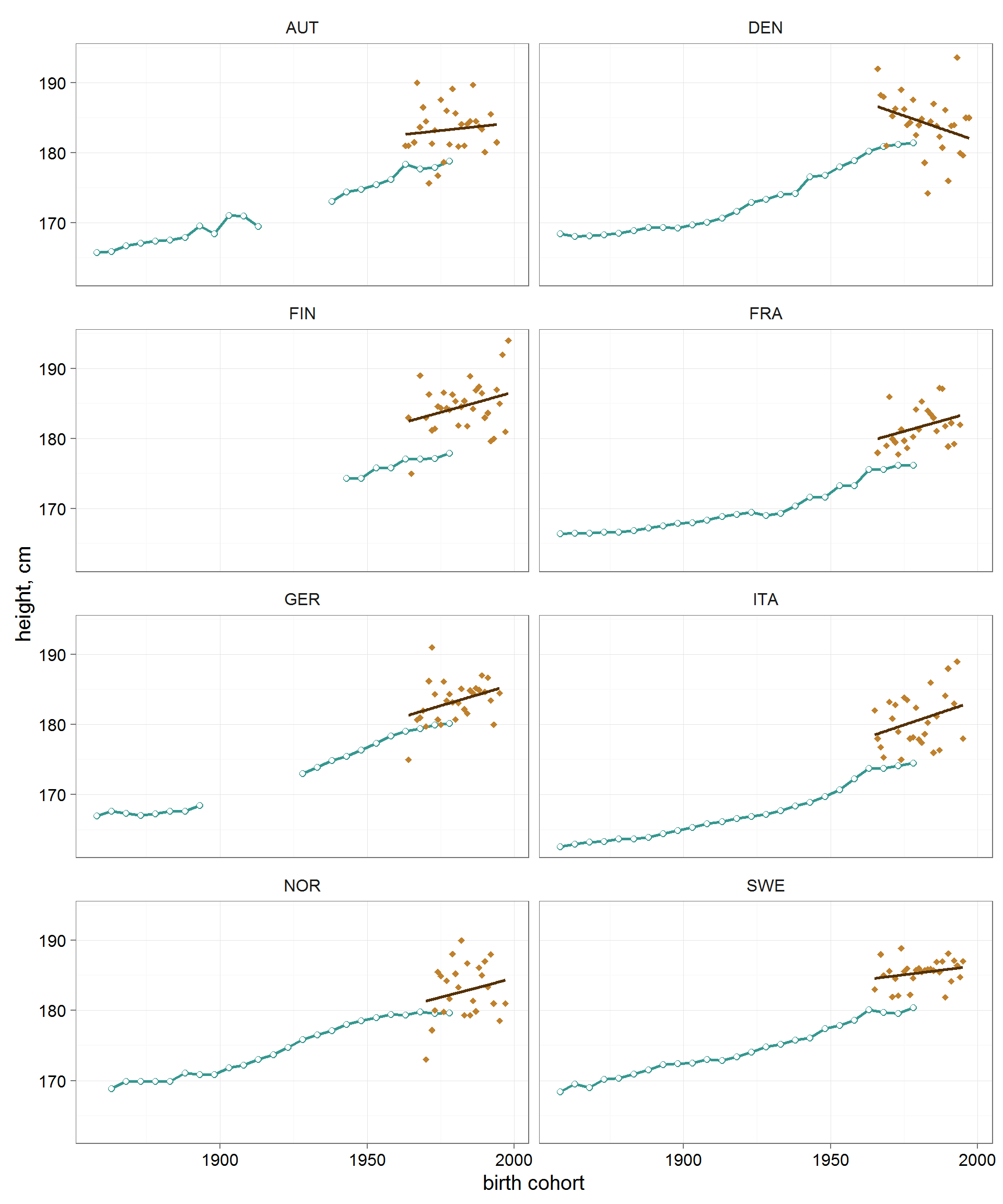
gg_hoc_vs_pop <- ggplot()+
geom_path(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop),
color=brbg11[9],size=1)+
geom_point(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop),
color=brbg11[9],size=2)+
geom_point(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop),
color='white',size=1.5)+
geom_point(data = df_hoc %>% filter(country %in% both_cnt), aes(x=cohort,y=h_hp),
color=brbg11[3],size=2,pch=18)+
stat_smooth(data = df_hoc %>% filter(country %in% both_cnt), aes(x=cohort,y=h_hp),
method='lm',se=F,color=brbg11[1],size=1)+
facet_wrap(~country,ncol=2)+
ylab('height, cm')+
xlab('birth cohort')+
theme_few(base_size = 15)+
theme(panel.grid=element_line(colour = 'grey75',size=.25))Во всех проанализировнных странах хоккеисты выше стеднестатистических мужчин на 2-5 см. Но это не удивительно — в спорте значительная селекция.
Примечательно другое. В развитых странах мира особенно бурное увеличение роста мужского населения происходило в первой середине 20 века. В когортах примерно 1960-х годов рождения рост мужчин приблизился к плато и пеерстал бурно увеличиваться. Тренд среднего роста хоккеистов во всех странах (кроме почему-то Дании) как будто бы продолжил приостановившийся многолетний тренд всего мужского населения.
Для когорт европейцев, родившихся в первой половине 20 века, темпы увеличения среднего роста варьировались от 1.18 до 1.74 см за десятилетие в зависимости от страны (рисунок 7). Начиная с 1960-х годов этот показатель опустился до уровня 0.15-0.80 за 10 лет.

# growth in population
df_hb_w <- df_hb %>% spread(cohort,h_pop)
names(df_hb_w)[2:26] <- paste('y',names(df_hb_w)[2:26])
diffs <- df_hb_w[,3:26]-df_hb_w[,2:25]
df_hb_gr<- df_hb_w %>%
transmute(country,
gr_1961_1980 = unname(apply(diffs[,22:24],1,mean,na.rm=T))*2,
gr_1901_1960 = unname(apply(diffs[,9:21],1,mean,na.rm=T))*2,
gr_1856_1900 = unname(apply(diffs[,1:8],1,mean,na.rm=T))*2) %>%
gather('period','average_growth',2:4) %>%
filter(country %in% both_cnt) %>%
mutate(country=factor(country,levels = rev(levels(factor(country)))),
period=factor(period,labels = c('1856-1900','1901-1960','1961-1980')))
gg_hb_growth <- ggplot(df_hb_gr, aes(x=average_growth,y=country))+
geom_point(aes(color=period),size=3)+
scale_color_manual(values = brbg11[c(8,3,10)])+
scale_x_continuous(limits=c(0,2))+
facet_wrap(~period)+
theme_few()+
xlab("average growth in men's height over 10 years, cm")+
ylab(NULL)+
theme_few(base_size = 20)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))На фоне стагнирующего тренда в населении увеличение роста хоккеистов выглядит весьма внушительным. А акселерация среди вратарей вообще беспрецедентна.
Не стоит забывать и про селекцию. Расхождение трендов в населении и среди хоккеистов, вероятно, свидетельствует об усиливающейся селекции — хоккей требует все большего роста для успешной карьеры.
Селекция в спорте
Проглядывая научную литературу по теме я наткнулся на примечательный результат. Оказывается, в профессиональном спорте преобладают люди, рожденные в первой половине года. Объясняется это тем, что спортивные секции, как правило, формируют детские команды по когортам рождения. Таким образом, рожденные в начале года, всегда имеют чуть больше прожитого времени за плечами, что зачастую прямо выражается в физическом превосходстве над сверстниками, рожденными под конец года. Нетрудно проверить этот результат на нашем датасете.

# check if there are more players born in earlier months
df_month <- df %>% mutate(month=month(birth)) %>%
mutate(month=factor(month,levels = rev(levels(factor(month)))))
gg_month <- ggplot(df_month,aes(x=factor(month)))+
geom_bar(stat='count',fill=brbg11[8])+
scale_x_discrete(breaks=1:12,labels=month.name)+
xlab('month of birth')+
coord_flip()+
theme_few(base_size = 20)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))Действительно, респределение довольно сильно смещено в сторону ранних месяцев. Если разбить данные по декадам рождения, то невооруженным глазом видно, что эффект усиливается со временем (рисунок 9). Косвенно это свидетельствует о том, что селекция в хоккее становится жестче.

# facet by decades
df_month_dec <- df_month %>%
mutate(dec=factor(substr(paste(cohort),3,3),labels = paste('born in',c('1960s','1970s','1980s','1990s'))))
gg_month_dec <- ggplot(df_month_dec,aes(x=factor(month)))+
geom_bar(stat='count',fill=brbg11[8])+
scale_x_discrete(breaks=1:12,labels=month.abb)+
xlab('month of birth')+
facet_wrap(~dec,ncol=2,scales = 'free')+
theme_few(base_size = 20)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))На будущее
Любопытно будет посмотреть, влияют ли физические данные на игровую статистику хоккеистов. Наткнулся на занимательную статью, опубликованную в очень приличном научном журнале, в которой авторы нашли корреляцию между соотношением пропорций лица хоккеиста и средним количеством штрафных минут за игру.
Reproducibility
Полный R скрипт, воспроизводящий результаты моей статьи, тут.
Использована версия R-3.2.4
Все пакеты по состоянию на 2016-03-14. В случае пакетных несовместимостей, данный код будет гарантированно воспроизведен при использовании пакета checkpoint с указанием соответствующей даты.
Комментарии (14)

ivanbolhovitinov
24.05.2016 11:20авторы нашли корреляцию между соотношением пропорциями лица хоккеиста и средним количеством штрафных минут за игру
Физиогномика в действии! Но кажется во взаимосвязи количества пиратов и глобальным потеплением лежат те же самые факторы, не?
ikashnitsky
24.05.2016 12:02Есть, конечно, определенное сомнение. Особенно по части количества наблюдений, на которых авторы строят выводы. Но! Попробуйте опубликовать корреляцию типа пираты-потепление в журнале уровня Proceedings of the Royal Society B: Biological Sciences. Да и по цитированиям можно заподозрить, что это не случайный результат, и он подтверждается аналогичными исследованиями.

ivanbolhovitinov
24.05.2016 12:23+2Графики выглядят очень натянуто. В графике, который прицеплен к статье: (а) точек мало, и (б) если убрать две крайние точки, то графика нет, есть пухлое облако. Это показывает огромный простор для возможности подтасовок.
Кроме этого мне интересно есть ли взаимосвязь facial width-to-height и роста (у длинных людей более вытянутые лица?). Если защитники в среднем более высокого роста, то должность их обязывает действовать более грубо.
Есть ещё такое распространенное мнение, что круглолицые более добродушны. Это может влиять на оценку их действий окружающими (их меньше наказывают). На подобный счет были интересные эксперименты с судейством бокса и дифференциации по цвету штанов боксера
(посредством цветокоррекции).
yorko
24.05.2016 12:46+1Ну в принципе считают, что на практике достаточно 10-20 наблюдений на одну независимую переменную, чтобы делать выводы о значимости влияния переменных на целевую. На cross-validated, конечно, задавался такой вопрос (и не раз).
Но все равно кажется, что это что-то из разряда spurious correlations. Или действительно скрытые факторы есть. Кстати, как авторы этой статьи пишут прямо в аннотации, пропорции лица не зависят от роста.
Но все равно такой вывод авторов «не удовлетворяет». А именно, последняя фраза аннотации «Together, these findings suggest that the sexually dimorphic facial width-to-height ratio may be an ‘honest signal’ of propensity for aggressive behaviour.» — это чисто «correlation doesn't imply causation».

ikashnitsky
24.05.2016 13:01+1Да, довольно сомнительно выглядят выводы, основанные на небольшом количестве наблюдений. При этом не согласен с вами, что регрессионный коэффициент сильно изменится, если убрать две крайние точки. Да, разброс точек вокруг регрессионной линии большой ("облако", residuals), но это говорит лишь об объясняющей силе модели; коэффициент при переменной от разброса не зависит. И чисто визуально: не сильно он изменится, если убрать крайние точки.
С ростом взаимосвязь не напрашивается. Скорее с комплекцией — индекс массы тела (отношение веса в килограммах к квадрату роста в метрах). А вот связь с амплуа точно должна быть. Но при этом защитники, как правило, и массивнее.
Последний аргумент вообще идет в разрез с обсуждаемым тезисом. В статье: чем шире морда — тем больше штрафа.

sp01
24.05.2016 12:27+2Отличная статья и интересные результаты.
Во вратари реально стали брать детишек повыше. У них обычно руки подлиннее, соответственно меньше времени на перекрытие площади при движении слева-направо или справа-налево, после отскока шайбы. Если маленькому вратарю придется делать движение всем корпусмо, то высокому достаточно дотянуться рукой.

varagian
24.05.2016 13:55+1Отличная статья, единственное, что хотелось бы — легенду и описание к графикам поподробнее, например на рисунке 5, как понял желтые точки — это хоккеисты, а синие — обычные люди (среднее по годам). Тогда немного непонятно, как может быть несколько желтых точек в один год, если это усреднение.

ikashnitsky
24.05.2016 14:17Спасибо. Очень справедливое замечание. В рисунке 5 лень было возиться с аннотацией при использовании
facet. Решил в подписи указать и забыл. Сейчас поправлю.
По сути. Все правильно — каждая точка это усреднение. Просто данные по населению агрегированы по пятилетним когортам, а для хоккеистов есть данные для каждого отдельного года рождения. На самом деле, там строго по одной точке на год. Просто ось
хочень сильно сжата для хоккеистов.





RoNikyo
Очень интересный результат касательно вратарей. Владислав Третьяк когда-то говорил, что его рост очень мешал, поскольку при броске низом он часто не успевал нагнуться чтобы поймать шайбу. В футболе вратари должны иметь большой рост и длинные руки для того, чтобы дотягиваться до краев ворот. В хокее же вратарь закрывает половину ворот собой и выгоднее брать не рослых, а более быстрых игроков. А тут за 30 лет 7 см. ХМ.
ikashnitsky
Да. Видимо, как-то резко изменилась вратарская техника. Мой коллега (он канадец, до 17 лет играл на самом высоком уровне в хоккей) сразу этот момент отметил, когда я только делился с ним планами статьи. Это то, что бросается в глаза — вратари стали значительно выше.
Heavyside
Насколько я знаю, в последнее время подавляющее большинство вратарей играет в стойке на коленях(баттерфляй), таким образом пропадает проблема того, что надо нагибаться, как Третьяку, и чем габаритнее вратарь, тем большую площадь ворот(а не пространства над ними, как ранее) он закрывает.
Про историю возникновения стиля: www.sport-express.ru/hockey/nhl/reviews/818655
И раз уж написал комментарий- пользуюсь случаем и благодарю за статью. Исследование подтвердило мои ощущения)
Ogra
Вратарская техника изменилась сильно.
Сравните Третьяка с Холтби. Они одного роста.
Apatic
Да, как уже писали выше, во времена Третьяка, вратарь, упавший на колени считался «отыгранным», а сейчас вратари на них садятся чуть ли ни при начале игры.

Думаю, тут сыграло роль и развитие хоккейной амуниции.
Во-первых, со стороны кажется, что сам вратарь стал занимать больше места в воротах (больше стали щитки и нательная защита?), во-вторых, лучше стали защитные свойства амуниции и уже не так страшно схватить шайбу в голову/шею (хотя, с другой стороны, скорость полета снаряда тоже возросла).
P.S. Историю развития вратарской амуниции в целом на просторах Сети не находил, а вот статьей про историю вратарских масок не могу не поделиться.