Голуби дают людям фору в решении дилеммы Монти Холла, что могло бы позволить им успешно выступать на одноименном ток-шоу. Это закономерность может, в свою очередь, излить свет на то, почему людям так трудно она дается.
Чем примечательна эта дилемма? При кажущейся простоте, она запутывает логические цепочки наших умозаключений, заставляя людей (но не голубей), в буквальном смысле, блуждать в трех соснах, вернее — в дверях. Это свойственно представителям самых разных культурных традиций: американцы, китайцы, шведы и бразильцы совершают одинаково неверный выбор.
Когнитивный психолог Massimo Piattelli-Palmarini заметил по этому поводу: Ни одна статистическая задача даже рядом не стоит по способности дурачить всех людей и во все времена.
В этой статье мы узнаем, в чем состоит дилемма, найдем теоретическое верное решение, проверим его в R, расскажем про интеллектуальную битву людей с голубями и узнаем ее результаты.
Дилемма Монти-Холла
Так называемая дилемма Монти Холла является хорошо известной загадкой, названной так в честь первого телеведущего на американском ТВ-шоу «Предлагаю Сделку», в которой тот давал участникам на выбор три двери, за одной из которой была машина, а за двумя остальными — козлы. Приз и козлы заранее расставлялись случайным образом и далее не меняли свои местоположения. После того как участник делал свой выбор, ведущий всегда открывал одну из оставшихся двух дверей, за которой, как он знал наперед, не было приза. Затем игроку предлагалась возможность поменять свой выбор или оставить все как есть.
На самом деле существует несколько возможных стратегий Монти.
- Адский Монти: ведущий предлагает сменить, если дверь правильная.
- Ангельский Монти: ведущий предлагает сменить, если дверь неправильная.
- Ведущий выбирает одну из коз и открывает её, если игрок выбрал другую дверь.
Классикой стала стратегия непредвзятости ведущего, когда он при любом изначальном выборе игрока открывает козло-дверь и предлагает поменять свой выбор или все оставить как есть. От нее мы и будем далее отталкиваться.
Подавляющее большинство игроков, опрашиваемых и испытуемых отказывались менять свой выбор, несмотря на то, что это удваивало их шансы на выигрыш. При этом люди мыслят, что в оставшихся двух дверях шансы на выигрыш равны и менять свой выбор нет никакого смысла. Если вы думаете так же, не смущайтесь, ибо не один вы заблуждаетесь.
Когда колумнист Mаrilin vos Savant[1] опубликовала решение в журнале Parade Magazine, на нее посыпался просто шквал писем читателей, выражающих свое несогласие. Вот например такие.
Я уверен, что скоро Вы получите много писем от студентов высших школ и колледжей. Возможно, Вам следует сохранить эти адреса, они помогут Вам в последующих выпусках.
W. Robert Smith, Ph.D. / Georgia State University
Я в шоке оттого, что даже после того, как Вас исправили по меньшей мере три математика, Вы все еще не видите свою ошибку.
Kent Ford / Dickinson State University
Ты сама коза.
Glenn Calkins / Western State College
Всего — около 10 тыс. писем. Как видим троллинг процветал еще в те времена, когда для этого нужно было потратить гораздо больше времени и усилий чем сейчас, а еще оплатить почтовый конверт и почтовую марку.
Талантливейший венгерский математик Paul Erdos также попался на уловку и отказывался даже принять решение, пока не увидел своими глазами компьютерную симуляцию результатов эксперимента. Честно говоря, с трудом в это верится, но молва пошла, тем не менее.
Разоблачение
Самое лаконичное объяснение решения ДМХ (Дилеммы Монти Холла) дано в круговой диаграмме.
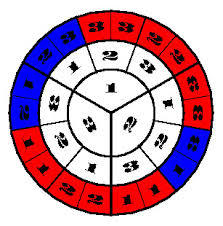
Внутренний круг показывает дверь за которой приз, средний круг указывает на первоначальный выбор участника а внешний — дверь, что откроет Монти. Последний также указывает на выигрышные расклады — они показаны красным цветом и их вдвое больше чем проигрышных синих. Простая арифметика показывает нам, что шансы выиграть при постоянном выборе равны 1/3, а смена выбора дает 2/3.
Рассмотрим теперь формальное решение задачи, на основе Теоремы Байеса об условной вероятности.
- Пусть А — событие, при котором машина за 1-й дверью.
- Пусть Б — событие, при котором Монти Холл открывает 2-ю дверь с козлом.
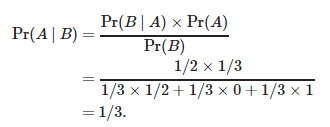
Pr(A) считается просто — 3 двери с одинаковой вероятностью выбора, значит машина за первой дверью с вероятностью 1/3. Вероятность нахождения приза в оставшихся двух одинакова, отсюда Pr(B|A)=1/2.
Рассчитать Pr(B), что в знаменателе, немного сложнее. Учитывая, что:
- Вы выбираете дверь под номером 1, а Монти показывает козла за дверью под номером 2.
- Если машина за 1-й дверью, то Монти с вероятностью 1/2 покажет дверь под номером 2.
- Если машина за 2-й дверью, то Монти всегда будет открывать дверь под номером 3, так как он никогда не показывает машину.
- Если машина за 3-й дверью, то Монти всегда будет открывать дверь под номером 2, так как он никогда не показывает машину.
Так и получается, что вероятность выигрыша равна 1/3, когда игрок не меняет дверь. Соответственно, смена двери, после демонстрации козла ведущим, равна 2/3.
А голуби что?
Немало изумленные косностью некоторых паттернов человеческого разума, исследователи Julia Schroder и Walter Hebranson задались целью проверить результаты на голубях, которые неплохо себя зарекомендовали в ряде практических теоретико-вероятностных задачах.
Пернатые и в этот раз не обманули ожиданий. После некоторой тренировки, голуби эмпирическим путем научились выбирать верную стратегию, а вот люди в том же эксперименте — нет.
Дело было так. Ученые отобрали шестерых заурядных сизых голубей и дали им на выбор три светящиеся кормушки. Следовал первоначальный выбор клювом, все три кормушки затухали и после недолгой паузы вновь начинали светится две, из которых голубь одну выбрал в начале. Компьютерная симуляция подменяла Монти Холла, убрав одну пустую кормушку, после чего испытуемое могло выбрать по-новой из оставшихся двух. Призом являлась еда — когда голубь верно угадывал кормушку, та открывалась и птица получала награду. Награда усиливала стимул и давала импульс к обучению. Затем появлялась новая тройка светящихся кормушек.
Птицы быстро научились считать свою выгоду и за 30 дней процент переключений кормушки вырос с 36.33% до 96.33%.
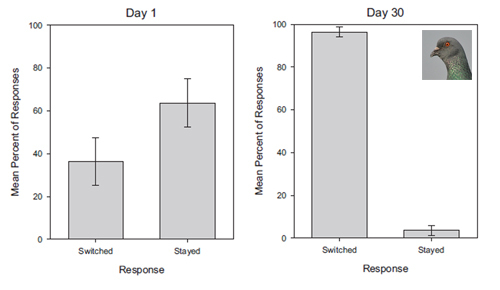
График роста голубиных показателей: на вертикальные линии над столбиками — доверительный интервал. Левый столбик показывает смену выбора а правый — тот же выбор. Некоторые птицы достигли абсолютных показателей — переключались всегда.
С людьми вышло иначе. За 30 дней эксперимента некоторый прогресс вначале наблюдался, но выявить тенденцию не удалось.
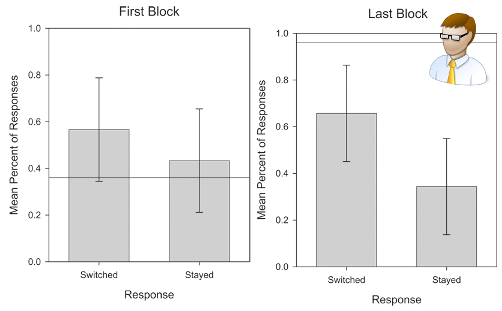
Рост надоев показателей с 56.67% до 65.67%. Границы доверительного интервала указывают на то, что выбор мог определяться случайностью.
Была проведена еще одна серия испытаний, в которых условия дилеммы Монти Холла ставились так, что выгоднее стало придерживаться изначального выбора. Целью было проверить способность мозга найти оптимальную стратегии даже когда условия неожиданно меняются. Во втором эксперименте, местонахождение приза фиксировалось только после первоначального выбора.
Результат подтвердил тенденцию. ЦОД голубиного мозга опять все верно рассчитал. С первый день ошибочной стратегии придерживались в 30.17% случаев, в последний же 15-й день — лишь в 4.33%. Результат юных home sapiens был едва отличим от его отсутствия: в первый день меняли выбор в 30%, в последний день — 27.67%.
Что все это значит?
В самом общем виде эти результаты можно интерпретировать следующим образом. Дело в том, как мы обучаемся и учимся оценивать вероятность событий. Чаще всего наша мысль бродит по отстроенным в годы обучения коридорам в поисках оценочной модели. Затем мы загоняем в нее данные и на выходе получаем готовый ответ. Часто берутся на вооружения всевозможные эвристические методы. В целом, это неплохо работает, но иногда случаются знатные фейлы, как в случае с ДМХ.
Альтернативой является эмпирический брутфорс: наблюдения, агрегация, вывод. Этот более трудозатратный и медленный способ принятия решений, но в данном случае именно он обеспечивает голубям выработку правильной стратегии.
Возможно ответ следует искать в серии статей про Логику Мышления. Человеческий и даже птичий мозг несет в себе еще много загадок, поэтому вместо спекуляций, в завершение темы, лучше попробуем эмуляцию ДМХ на R. Вывод скрипта русифицирован.
5:543)$ R -f monty.r
Monty Hall Problem Simulation
"Оставить прежний выбор"
Выигрыш = 3380
Количество повторов = 10000
Наблюдаемое соотношение выигрышей = 0.338
Соотношение выигрышей в теории = 0.3333333
"Изменить выбор"
Выигрыш = 6620
Количество повторов = 10000
Наблюдаемое соотношение выигрышей = 0.662
Соотношение выигрышей в теории = 0.6666667>
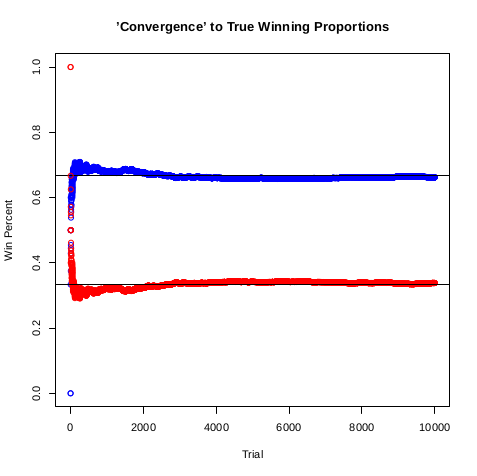
> ## Plot 'convergence' to true winning proportions
> ## Blue is switching doors, red is staying
> plot.new()
> plot(cumsum(changewin) / c(1:N), main = "'Convergence' to True Winning Proportions",
+ xlab = "Trial", ylab = "Win Percent", ylim = c(0, 1), col = "blue")
> abline(h = 2/3)
> points(cumsum(staywin) / c(1:N), type = "p", col = "red")
> abline(h = 1/3)График асимптотической сходимости к вероятностям 1/3 и 2/3.
Использованные материалы
- Are Birds Smarter Than Mathematicians? Pigeons (Columba livia) Perform Optimally on a Version of the Monty Hall Dilemma
- Pigeons Beat Humans at Solving 'Monty Hall' Problem
- Pigeons outperform humans at the Monty Hall Dilemma
- Monty Hall Problem: Intuitive and Mathematical Solutions
- ^Автор колонки Ask Merilin, обладатель рекорда Гиннеса за самый высокий IQ.
Комментарии (290)
Zolg
27.10.2016 00:10+13Для интуитивно-психологического понимания задачи можно представить, что дверей не 3, а 100. И 98 открыты после выбора. Т.е. машина точно за одной из двух дверей, но вероятность того, что вы с первого раза выбрали нужную, как вы помните — 1%
Monoroch
27.10.2016 00:14-6И вообще ничего не изменится. В итоге будет новый выбор с 2 равновероятными вариантами.
valergrad
27.10.2016 00:28+30Где-то в этот момент средний голубь бы уже понял свою ошибку. Интересно, как скоро ее поймете вы :)
( Hint: нет никакого нового выбора, машина была спрятана за одной из дверей еще до того как вы выбирали и никуда не переезжала).
ivlis
27.10.2016 00:38-2Если вы знаете за какой дверью машина, то зачем выбирать вообще?
Dim0v
27.10.2016 08:24+19Вы не знаете. Знает ведущий. И открывая двери, за которыми заведомо нет машин, он этой информацией делится (частично) с вами.
Вот еще одно «интуитивное» объяснение: пусть вы выбрали дверь 1. Вероятность того, что машина за ней — 1/3. Вероятность того, что машина за дверью 2 или 3 — 2/3. После того, как ведущий открыл одну из дверей эти вероятности не изменились: для первой двери это по прежнему 1/3, а для 2 или 3 двери — 2/3. Но, благодаря информации от ведущего, вероятность для пары дверей 2-3 делится между ними не пополам (по 1/3, как это было до открытия двери ведущим), а полностью «переходит» к одной из дверей, так как за второй машины точно нет.alibertino
27.10.2016 10:23-4Почему для первой двери вероятность не изменилась? Почему переходит полностью на оставшуюся? По-моему переходящая вероятность как раз таки делится на выбранную вначале дверь и оставшуюся?
Dim0v
27.10.2016 14:16+1Почему для первой двери вероятность не изменилась? Почему переходит полностью на оставшуюся?
Потому что ведущий не может открыть ту дверь, которую мы выбрали изначально. Соответственно, перераспределять вероятности, открывая двери, он может только между невыбранными дверями.
Если бы он мог открыть любую дверь без машины (в том числе и выбранную) — то да, между оставшимися двумя дверями вероятность распределялась бы поровну. Но это не так.
Gearbeast
27.10.2016 12:51А как быть если с первого раза угадал где машина?
То есть с вероятностью 1/3 угадал, где машина и с вероятностью 2/3 предлагают неверный выбор?Dim0v
27.10.2016 14:20+1Вы, видимо, не совсем понимаете, что значит вероятность и как она работает.
Если достоверно известно, что машина за той дверью, которую вы выбрали изначально, то вероятность того, что вы угадали — 1, а не 1/3. А если достоверно известно, что машина не там, то вероятность — 0. Но ни один из этих случаев не имеет отношения к исходной задаче, потому что в ней игроку неизвестно, где машина.Gearbeast
27.10.2016 14:40+1Не то что «не совсем понимаю», вообще не знаю, только на уровне собственного опыта и чувств/ощущений.
Тут, на мой взгляд, проблема в другом. Если я воспринимаю эту ситуацию как математическую задачу, то, да, я понимаю, что у не выбранной двери ведущим шанс 2/3, а у той, которую выбрал я, 1/3. И если будет многократный повтор выбора, то вторую попытку нужно изменять на дверь с шансом 2/3. Это действительно более выигрышная стратегия.
Но вот если рассматривать ситуацию как единственный выбор, как участие в игре, то шанс выигрыша становится 50 на 50, один к двум и все в том же духе, после открытия одной двери для участника (не для математики или теории вероятности). Это ближе к психологии.
Интересно было бы посмотреть статистику этой игры (именно игры, а не тестов), хотя предполагаю, что у сменивших дверь во «втором туре» процент победы выше.Dim0v
27.10.2016 20:13Но вот если рассматривать ситуацию как единственный выбор, как участие в игре, то шанс выигрыша становится 50 на 50, один к двум и все в том же духе, после открытия одной двери для участника (не для математики или теории вероятности).
Ну по такой логике для одного человека вероятность заболеть простудой и бубонной чумой тоже одинаковая — 50 на 50, один к двум и все в том же духе. Либо заболеешь, либо нет.
Звучит абсурдно, по моему.
Для одного человека (при условии, что он не знает, где машина), выгоднее менять свой первоначальный выбор. И вероятности будут не 50/50, а 33/66.
Интересно было бы посмотреть статистику этой игры (именно игры, а не тестов)
Можете пояснить, что вы имеете в виду под «тестами» и под «игрой», и чем они отличаются?Gearbeast
28.10.2016 11:05Тесты — это где группа одних и тех же людей участвует в этой ситуации многократно (они вроде как не обучаются и процент их побед ниже, чем у голубей).
Игра — это каждый раз новый человек участвует и у него нет возможности обучаться.
Соглашусь с Сергеем (@sebres) основная проблема не понимания (у тех кто не понимает почему шанс выиграть при смене двери 2 к 3) в том, что рассматривается одна конкретная ситуация, а не последовательность ситуаций.
Сам еще не до конца принял, и как бы повел себя в ситуации игры (единственное, один раз) не знаю.
В ситуации тестов (многократного повторения, участия) точно бы менял дверь во втором «туре».
Ниже (почти в конце) Caullerd привел статистику смены выбора двери и без смены, она очень наглядно показывает где шансы больше.Dim0v
28.10.2016 16:07Тесты — это где группа одних и тех же людей участвует в этой ситуации многократно (они вроде как не обучаются и процент их побед ниже, чем у голубей).
Игра — это каждый раз новый человек участвует и у него нет возможности обучаться.
А как, простите, обучение человека на выбор одной из нескольких стратегий (в данном случае — одной из двух — менять либо не менять) влияет на эффективность этих стратегий?
основная проблема не понимания (у тех кто не понимает почему шанс выиграть при смене двери 2 к 3) в том, что рассматривается одна конкретная ситуация, а не последовательность ситуаций.
Опять таки, какая разница, сколько ситуаций рассматривается? По вашему, для одного эксперимента вероятность одна, а для нескольких (независимых друг от друга) — другая?
Ниже (почти в конце) Caullerd привел статистику смены выбора двери и без смены, она очень наглядно показывает где шансы больше.
Да, и там наглядно видно, что при смене двери вероятность победы в 2 раза выше. И там никакого обучения не происходит. Первая программа всегда меняет дверь, вторая — никогда не меняет. И ни одна из них ничему не учится в процессе. То есть, если я правильно вас понял, программы Caullerd'а подходят под ваше определение «игры, а не тестов». Как, кстати, и почти все прочие симуляции этой задачи.Gearbeast
28.10.2016 16:55А как, простите, обучение человека на выбор одной из нескольких стратегий (в данном случае — одной из двух — менять либо не менять) влияет на эффективность этих стратегий?
Ни как, я ради собственного интереса хотел бы посмотреть статистику.
В тестах человек должен был бы научиться, а этого, вроде как, не происходило. Статистика у людей в тестах хуже, чем у голубей.
Опять таки, какая разница, сколько ситуаций рассматривается? По вашему, для одного эксперимента вероятность одна, а для нескольких (независимых друг от друга) — другая?
На мой взгляд, именно в этом вся проблема. Конкретная ситуация (игра) против эксперимента. И получается одна часть людей рассматривает, как эксперимент, и получает шанс 2 к 3, а другая часть людей рассматривает, как игру и не может поверить в этот шанс. Этот момент надо рассматривать с психологической точки зрения, я сам не мог поверить в шанс 2 к 3 выиграть при смене двери, пока не вывел сознание из ситуации игры. Пока я мысленно стоял перед дверьми и «надеялся» выиграть, я не мог поверить в шанс 2 к 3, если во втором «туре» сменю дверь. И даже сейчас, когда я пониманию, что выбрав другую дверь у меня больше возможности выиграть, сделать реальный выбор в пользу другой двери тяжело, потому что остается какая-то надежда, что машина за дверью, выбранной сначала.
Проведите единственный эксперимент: Попросите кого-нибудь дома спрятать за одной из дверей Ваш ужин, потом «ведущий» откроет одну дверь, за которой нет ужина. И у Вас будет шанс сменить дверь или оставить ту, которую выбрали изначально. Будете менять? Ужин лучше заменить, чем-то более ценным и на больший срок.
Вот тогда Вы почувствуете проблему выбора, может быть, если «приз» будет действительно ценным.
Да, и там наглядно видно, что при смене двери вероятность победы в 2 раза выше. И там никакого обучения не происходит. Первая программа всегда меняет дверь, вторая — никогда не меняет. И ни одна из них ничему не учится в процессе. То есть, если я правильно вас понял, программы Caullerd'а подходят под ваше определение «игры, а не тестов». Как, кстати, и почти все прочие симуляции этой задачи.
Да, подходят.
Это, конечно, не большая выборка (по тысяче на каждый вариант). Но по ней не выходит 2 к 3. Если взять в процентах 1 к 3 это примерно 33.3, 2 к 3 примерно 66.6.
А по результатам Caullerd`а получается 1 к 3 — 37, а 2 к 3 — 60,4.
Спишем на погрешность и малую выборку
Интересно было бы посмотреть на большей выборке.shurupkirov
31.10.2016 07:43В тестах человек должен был бы научиться, а этого, вроде как, не происходило. Статистика у людей в тестах хуже, чем у голубей.
Потому что тестирование не одинаковое:
Голуби 30 дней с призами
Люди 200 раз без призов
Caullerd
31.10.2016 16:05К сожалению, тут сыграла не малая выборка, а ошибка при написании кода.
Я увеличил количество игр на пару порядков, и результаты остались теми же, примерно 37% и 62%.
Оказалось, что из-за неверных параметров функции вычисления случайного значения, которая возвращала случайное число от 1 до 3 для задания «призовой» двери и начального выбора игрока — примерно в 50% случаев возвращалось значение 2, а 1 и 3 делили между собой по 25%.
После корректной настройки, когда все числа получили ~33% вероятности выпадения — итоговые результаты стали следующими:
Всегда меняем свой первоначальный выбор.
В среднем выиграно в 10000 партий по 100 игр: 66.557
Всегда настаиваем на первоначальном выборе.
В среднем выиграно 10000 партий по 100 игр: 33.313
Как видно, все пришло в соответствие с теорией.
Насчет проблемы смены выбора, я вас прекрасно понимаю. Хотелось бы сказать, что ваш вариант с ужином еще не самый интересный :)
Скажем, вы в реальности стали жертвой ведущего-маньяка, который хочет «сыграть с вами в игру»: предлагает вам выбрать дверь, за которой ключ к свободе, а за другими — мучительная смерть (предположим, что он честный маньяк, и ему не интересно во все смерть засовывать, давая вам ложную надежду.)
Тут уже страх сменить дверь на смертельную будет ох каким немаленьким. Но если успокоиться и подумать, даже если это может стать вашим последним выбором в жизни, стоит ли верить в 33 процента больше, чем в 66?
sebres
27.10.2016 20:35-1Вооот! Искал этот комментарий (и дождался от человека, по его словам ничего не понимающего в "вероятностях" ;).
На самом деле спорящие стороны обе частично правы, ибо дилема происходит из-за неполного (вернее куцего что-ли) определения условий задачи… И голуби тут не совсем как-бы причём...
Если рассматривать вероятности угадывания при смене двери и без, при как минимум 3-х повторах (т.е. строго говоря соблюдая необходимое правило для оценки вероятности — массовый характер, желательно бесконечно долго), тогда — да все как написано — дверь нужно менять.
Если рассматривать вероятность угадывания один единственный конкретный раз (исключая условие "массовый характер" и предыдущие "опыты" других людей), то вероятности (нет уже нельзя говорить про вероятности, мат-ожидания и иже с ними), скорее необходимости что-ли менять дверь — как таковой — нет. Ибо равновероятно, что во втором туре именно в этот (важный для вас) раз — вы получите машину. Т.е. в этом конкретном туре она равна 1/2 (независимо от смены двери). И это кстати также видно на той же картинке из википедии — из 6-и человек 3-м досталась машина и 3-м — коза. Просто люди обращают внимание только на нижний левый угол (когда дверь меняли). Но… в том то и дело, что в
одномединственном конкретном случае абсолютно не важно менялась дверь или нет, ибо изначально равновероятно она могла быть уже выбрана верно.
Комбинаторика наряду с теорией вероятностей, очень строгая наука, где для точного анализа, условия задачи должны быть строго оговорены. Многие кстати путают вернее иногда неверно связывают частотные и вероятностные характеристики (например количество
равновероятныхкомбинаций и вероятности их выпадения в зависимости от различных условий).
- В качестве примера чуть поменяем условия (исключая необходимое условие бесконечности проведения опытов): Это шоу происходит один единственный раз (от слова совсем). Поможет ли играющему смена двери выиграть машину, по сравнению с тем как если бы вы ее не меняли? Ответ — нет.
- Другой пример: Ежедневное шоу. Насколько быстрее у компании, осуществляющей "бесплатную" раздачу машин, закончатся деньги, если каждый участник всегда будет менять дверь (по сравнению с тем как если бы ее всегда не меняли)? Ответ — в два раза быстрее (2/3 в сравнении к 1/3).
Ну и возвращаясь к голубям, учитывая что делая это раз за разом "смена двери" действительно повышает шансы добраться до корма, делается вывод — нужно менять дверь. Что не отменяет тот факт, что в единственном конкретном случае (а человек участвует в шоу ровно один раз), это абсолютно не важно (если не ставить целью разорить фирму, проводящую шоу).
Поэтому многие именитые математики и сделали такие заявления, т. к. подходя к задаче комбинаторно, они рассматривали единственное действие, т.е. выигрыш конкретного участника, а не общий игровой фонд всех участников за год, с целью разорения фирмы (т. е. при многократно повторяемых шоу).
allcreater
27.10.2016 22:17Конечно, у сменивших дверь процент победы выше. 66.(6)%, как и вытекает из теории вероятности. От того, что Вы сыграете в игру один раз, а не сто, ситуация не изменяется: смена выбора увеличивает вероятность выигрыша, потому что ведущий делится информацией, и отказаться от смены двери — отказаться от подсказки.
sebres
28.10.2016 00:35+1отказаться от подсказки...
а теперь представим, что первый раз вы не выбирали дверь… ведущий же все равно откроет дверь с козлом. Т.е. что изменилось — вы тыкаете в какую-то дверь (вероятность выбора правильной в этом случае один к двум), как на это влияет выбрана она была до этого или нет?
нет про частотный анализ и мат ожидание не нужно, это понятно как раз, вы ответьте на прямо поставленный вопрос...
ПС Если, что вопрос не мой, задаёт профессор хановерского университета… я его втянул в дискуссию
Dim0v
28.10.2016 01:13+1что изменилось
Изменилась постановка задачи. Теперь ведущий может открыть любую из дверей с козлами и вероятность выбрать после этого дверь с призом действительно становится 50%.
В исходной же задаче ведущий не может открыть ту дверь, которую выбрал игрок. Таким образом, если игрок изначально выбрал дверь с козлом (а вероятность этого — 2/3, кстати, с этим вы согласны или тут, по вашему, тоже 50 на 50?), то у ведущего нет выбора — он может открыть только одну единственную дверь с козлом. А за второй дверью будет приз, который и получит игрок, если поменяет свой выбор. Если же изначально была выбрана дверь с призом (а вероятность этого события — 1/3), то ведущий может выбрать, какую из оставшихся дверей открыть. И в обоих случаях игрок проиграет при смене своего выбора.
Путем совсем несложных подсчетов, можем теперь получить и общую вероятность выигрыша при смене двери:
2/3 (вероятность выбора козла изначально) * 1 (вероятность того, что после открытия двери ведущим за второй дверью будет приз) + 1/3 (вероятность выбора приза) * 0 (все та-же вероятность того, что после открытия двери ведущим за второй дверью будет приз) = 2/3 * 1 + 1/3 * 0 = 2/3
Для вашей же задачи, где мы дверь изначально не выбираем, а только после открытия ведущим одного из козлов, мы имеем вероятность 1/2, потому как просто выбираем уже из двух дверей и выбор игрока никак не ограничивает свободу действий ведущего.sebres
28.10.2016 01:44не может открыть ту дверь, которую выбрал игрок.
вы таки не поняли или я не понятно объяснил: что меняет выбранная дверь, или вернее какого козла ведущий откроет — первого или второго? т.е. первоначальный выбор не изменяет ничего, дверь с козлом будет открыта все равно, второй выбор (ткнуить снова в ту же дверь или в другую) ничего не меняет… убрав одного из козлов, это ведущий изменил условия задачи, сравняв вероятности машины для обеих оставшихся дверей, вне зависимости от "клейма" предыдущего выбора.
"ваша" математика понятна и в случае команды игроков и многократных повторов, без обмана — все так, что не отменяет всего выше описанного для каждого конкретного игрока...
Dim0v
28.10.2016 04:06+1какого козла ведущий откроет — первого или второго?
Конкретный козел действительно не важен. Значение имеет количество дверей, доступных ведущему для открытия. «Запрещая» ему открывать одну из них (выбрав ее) игрок получает преимущество по сравнению с ситуацией, где такого запрета нет.
т.е. первоначальный выбор не изменяет ничего, дверь с козлом будет открыта все равно, второй выбор (ткнуить снова в ту же дверь или в другую) ничего не меняет…
Меняет. И я описал в предыдущем комментарии, как именно меняет.
убрав одного из козлов, это ведущий изменил условия задачи, сравняв вероятности машины для обеих оставшихся дверей
В вашей задаче, где ведущий может открыть любую дверь — да, сравнял. В исходной задаче, где он не может открыть выбранную дверь — нет, там вероятности 33/66.
в случае команды игроков и многократных повторов, без обмана — все так, что не отменяет всего выше описанного для каждого конкретного игрока...
То есть вы хотите сказать, что для одного отдельного игрока вероятность 50/50, но если таких отдельных игроков взять много, то для них она будет 33/66?
П.С. еще из соседней ветки
И это кстати также видно на той же картинке из википедии — из 6-и человек 3-м досталась машина и 3-м — коза.
Если вы внимательно посмотрите на картинку, то заметите, что из этих 6 человек 3 меняли свой выбор, а 3 — не меняли. Так что совсем не удивительно, что в результате у троих есть машина, а у троих нет: 1/3 (вероятность выиграть, не меняя дверь) * 3 (не меняли свой выбор 3 человека) + 2/3 (вероятность выиграть, меняя дверь) * 3 (меняли свой выбор тоже 3 человека) = 1/3 * 3 + 2/3 * 3 = 3.
Если бы все 6 человек не меняли дверь, то победителей было бы 4, а не 3.
Falcon_peregrinus
28.10.2016 14:59В любом случае, это стопроцентная угадайка, так как подсказок, за какой дверью автомобиль, так и нет. Так что во всех случаях выбор будет случайным, а конкретные цифры (1/3 или 2/3) всё равно ничего особо не решат для данного конкретного игрока.
Dim0v
28.10.2016 16:15+1а конкретные цифры (1/3 или 2/3) всё равно ничего особо не решат для данного конкретного игрока.
Представьте ситуацию: есть 2стуластола, на которых стоят непрозрачные коробки. На одном столе 2, на втором — 100. При этом, в одной коробке на каждом столе лежит по 1000 долларов, а остальные — пустые. У вас есть возможность показать пальцем одну любую коробку и забрать ее со всем содержимым. С какого стола будете брать?
Следуя вашей логике, конкретные цифры (1/2 или 1/100) тут тоже ничего особо не решат для данного конкретного игрока. Так как
это стопроцентная угадайка, и подсказок, в какой коробке деньги, так и нет. Так что во всех случаях выбор будет случайным.
sebres
28.10.2016 01:49-1кстати, все бы изменилось, если бы первый выбор что-то менял, например вылет или выигрыш игрока, неравнозначность козлов А и Б, и т.д.
alexandr_kukolev
27.10.2016 22:17Речь ведь не об угадывании, а о выборе стратегии принятия решения. Да, возможно вы действительно угадали. Шанс на это 1/3. А вот шанс на то, что не угадали — 2/3. Следовательно, если ваша стратегия выиграть — вы выберите вариант с наибольшей вероятностью выигрыша (спасибо кэпу, что подсказал эту формулировку )).
kalempir
27.10.2016 12:51Очень странно, но эту задача меня достала. :) Друг мой рассказал эту задачку, и я сказал что не буду строго выбирать, а брошу монетку и шансы у меня будут 50 на 50. Он утверждал что если поменяю свой первоначальный выбор, то шансы на выигрыш у меня будут 2/3, то есть условно открытая дверь ведущим плюсуется к шансом другой двери. В этом и была загвоздка, я никак не мог понять почему плюсуем. Затем начали экспериментировать на стаканчиках. И тут я увидел как это происходит. И так
Zolg
27.10.2016 01:06+5встретить, или не встретить динозавра на улице тоже, простите равновероятные события (потому что два)?
vics001
27.10.2016 02:31+1Равновероятность — это математическое понятие, а не интуитивное. Если мы будем проводить эксперимент и кидать монету и посчитаем после этого, то будет 50 на 50. Если будем звать людей выбирать из двух дверей, то будет тоже 50 на 50. А если позовем математика выбирать, то будет 99%.
Правильный ответ, у вас вероятность выиграть 50%. А у математика 99%. Здесь нет противоречия, математик выигрывает в среднем 99 из 100, а вы 1 из 2.
radrig0
27.10.2016 14:07Математик выбирает другую дверь в среднем 99 из 100. Голуби в 96,33% случаев выбирали другую дверь. Но вот в скольких процентах этот вариант оказался выигрышным? Это уже совсем другой вопрос.
Color
27.10.2016 15:452/3 же
radrig0
28.10.2016 08:15Именно. Но никак не:
Правильный ответ, у вас вероятность выиграть 50%. А у математика 99%. Здесь нет противоречия, математик выигрывает в среднем 99 из 100, а вы 1 из 2.
Gurklum
28.10.2016 18:00Если проследить конкретную ветку, можно увидеть, что там выбирают из двух дверей, когда изначально их было 100.
Поэтому в той задаче будет 99%. Потому что математик будет выбирать «другую» дверь всегда.
smaugfm
27.10.2016 08:24То есть, если эти варианты равновероятны, а изначально вероятность выбрать дверь с машиной была 1/100 — то теперь эти 2 равноявероятных варианта каждый равны 1/100… но ведь их сумма должна быть равна единице.
SilverHorse
27.10.2016 08:25+3Не равновероятными.
Поясню на основе «парадокса» детей:
1) Вероятность рождения мальчика 1/2. У человека двое детей, один из них мальчик, какова вероятность того, что второй — девочка?Ответ2/3. Эквивалентный вопрос: из бесконечного множества людей с равновероятным выбором того или иного пола нам выбрали двух человек, один из них мужчина, какова вероятность, что второй — женщина?niknamezanat
27.10.2016 12:51+1Вторая задача сформулирована как-то не так. От добавления прилагательных «младший-старший» смысл от первой не меняется.
«Вероятность рождения мальчика 50%. У человека двое детей, какова вероятность того, что они разнополые » Даст ответ 1/2.SilverHorse
27.10.2016 20:14+2Меняется. Мы меняем пространство элементарных исходов. К слову, в этом же заключается «неоднозначность» трактовки первого случая, описанная в статье в Википедии ниже. Когда мы упорядочиваем набор детей и начинаем их проверять одного за другим с соответствии с установленным отношением порядка, это становится эквивалентно последовательности независимых испытаний в виде выборки из бесконечного множества (перебор детей одного за другим равносилен наблюдению их рождения друг за другом в случайно взятой семье). В этом случае мы перестаем выбирать из конечного пространства элементарных исходов, в котором вероятность нахождения элемента в наборе определена предварительной выборкой, мы начинаем выбирать из потока независимых событий, формируя этот набор заново.
И возвращаясь к вашей модификации формулировки. «Разнополые» != «один из них мальчик», поскольку в первом случае мы включаем в пространство исходов вариант «две сестры», перебирая все 4 возможные комбинации (ММ, МД, ДМ, ДД), а во втором вариант «две сестры» отсутствует, исключенный условием «один из них мальчик»… но все это справедливо, если мы смотрим на семью целиком, рассматривая наборы из двух предварительно выбранных элементов, если же мы берем и проверяем детей по очереди, то вероятность автоматически становится 1/2, потому что от факта установления пола одного ребенка пол другого не зависит никак — его вероятность быть совпадающим или отличным от первого всегда была и будет 1/2 (гомозиготных близнецов не считаем, само собой :) Хотя их тут и быть не может, вероятность мы определяем для рождения одного человека же).niknamezanat
28.10.2016 10:03+1Да, я был не прав, Старшинство мальчика ограничивает выбор только до двух возможных вариантов. (я сначала забыл исключить вариант мальчик и старшая девочка, поскольку он практически сливается с вариантом старший мальчик и девочка)
n_demitsuri
27.10.2016 14:06Разве в первом вопросе ответ 2/3? https://ru.wikipedia.org/wiki/Парадокс_мальчика_и_девочки
iassasin
27.10.2016 08:252 равновероятных вариант будет только в том случае, если рассматривать это как новую задачу. Но у нас задача изначально другая.
Изначально 3 двери, за 2-умя их них козлы. Значит шанс ткнуть неправильную дверь = 2/3. Монти-Холл в любом случае откроет дверь с козлом. А значит в 2 из 3 случаев если мы изменим выбор, то попадем на выигрышную дверь (т.к. вторая проигрышная уже открыта Монти-Холлом, а первую мы выбрали сами).
meft
27.10.2016 12:17нет, это не равновероятные варианты. По крайне мере для человека, который знает, какую дверь выбрали в первый раз.
Это выбор между вероятностью 1/2 и 1/3. Приведите к общему соотношению и получите соотношение 3 к 2.
mpakep
27.10.2016 10:56Еще проще если увеличить а сокртить количество вариантов до двух.
Представьте что двери всегда две. После вашего укадывания ведущий открывает одну дверь (всегда неверную)
После этого остается всегда верный вариант и ваши шансы после того как ведущий открыл дверь всегда 100%
Barafu
27.10.2016 01:03+2Люблю поверять ерунду брутфорсом.
Код на Питонеfrom random import sample, randint tests = [(1,0,0),(0,1,0),(0,0,1)] #Просто рандом def get_r(): return randint(0,2) #Выбор наугад def rand_guesser(t_num): guess = get_r() return tests[t_num][guess] #Смена выбора после открытия двери def educated_guesser(t_num): test = tests[t_num] pre_guess = get_r() #Первичный угад excluded_door = None for i in range(3): #Открываем одну дверь if test[i] == 0 and i != pre_guess: excluded_door = i break else: print (test, pre_guess) assert False, "That error, you know" variants=set([0,1,2]) variants.remove(excluded_door) variants.remove(pre_guess) #возвращаем оставшуюся дверь assert len(variants) == 1 return test[variants.pop()] r_sc=0 e_sc=0 for i in range(100000): s = randint(0,2) r_sc += rand_guesser(s) e_sc += educated_guesser(s) print(r_sc, e_sc)Barafu
27.10.2016 01:15+11Вообще, на бытовом уровне это можно объяснить так. Вы выбираете случайно между призом и двумя козлами. Вероятность, что ваш выбор — это приз — 1/3. Затем ведущий убирает одного козла. (это предложение не является призывом к свержению государственной власти). Отвлёкся. Убирает одного козла. Вы ничего не делаете, вероятность того, что вы выбрали приз по прежнему 1/3. Значит, на втором оставшемся варианте — оставшиеся 2/3.
1vanK
27.10.2016 01:48+2Это часть ответа, потому что после этого остается вопрос, почему изменилась вероятность неоткрытой и невыбранной двери, а вероятность выбранной двери не изменилась? И тут в ход идет то, что ведущий не может открыть дверь, которую выбрал игрок, что влияет на вероятность.
sams0m
27.10.2016 08:26+3Спасибо. Вот после вашего комментария я наконец понял как это работает. Все предыдущие комменты меня не убеждали что вероятность не 50%.
alexkbs
27.10.2016 10:12-4Если вы всё ещё сомневаетесь, то такое объяснение:
Представьте перед внутренним взором три двери, одну из которых вы выбрали. После того как ведущий откроет одну из дверей, за которой ожидаемо оказывается козел, остаются две двери. Одну из них вы выбрали… Теперь отложите в сторону логику и разум, прислушайтесь к себе. Какая из этих дверей более интересная? Та дверь, которую вы выбрали, или другая, которую почему-то не выбрал ведущий?
3aicheg
27.10.2016 11:21+2Кроме того, он не может открыть и дверь с призом, что, вроде бы, тоже важно. Где-то попадалась статья с рассуждениями, что если ведущий сам не знает, где приз, и наугад открывает одну из дверей, и там случайно оказывается козёл, то менять свой изначальный выбор нет смысла. Если я ничего не путаю, потому что когда я начинаю думать над этой задачей, меня начинает глючить. Надо ещё одну симуляцию написать…
alff31
28.10.2016 12:48Да, в этом случае менять нет смысла, зато если ведущий сам не знает где приз, то появляется вариант, что может случайно открыть дверь с призом.
Если в этом случае приз, обнаруженный ведущим, дают вам, это аналогично смене двери в исходной задаче, вероятность выигрыша становиться 2/3.
marenkov
27.10.2016 12:29Думаю автору статьи стоит добавить это объяснение в текст.
P.S. Сам пришел к такому же интуитивно-логическому объяснению.
hdfan2
27.10.2016 13:12+1Вы намекаете, что если в голосовании два тура, то во втором нужно голосовать не за того же кандидата, что и в первом?
Eldhenn
27.10.2016 15:26> вероятность того, что вы выбрали приз по прежнему 1/3
Почему, если дверей уже две?..
3aicheg
27.10.2016 04:15+1Я когда-то для иллюстрации знакомым гуманитариям написал симулятор на джаваскрипте: https://jsfiddle.net/rmbzhona/
Вводим число испытаний (допустим, 100), жмём «Go!», жёлтая полоска показывает, сколько раз из этих ста мы бы выиграли, не поменяв выбор, а красная — поменяв.
Надо заметить, что задача, по-сути, тавтология — это окончательно понимаешь, записывая вероятности в программе: одна дверь из трёх равна одной третьей, а из двух — двум третьим…
vitvad
28.10.2016 20:50я вот тоже решил написать на JS и проверить.
написал — получил 33% и 50% соответственно и долго пытался понять что я сделал ну так…
а потом присмотрелся к вашему решению.
if(which_door()) {initial++;} else {changed++;}
где
which_door()
у вас возвращает ```true``` or ```false```
и теперь внимание initial вы получаете 33% равный теоретическому шансу на выигрыш, а в changed у вас 66% тех которые вы не угадали, а не тех когда вы сменили выбор и угадали.
my JS solution// rand int from min (inluded) to max (excluded) [MDN example] function randRange(min, max){ return Math.floor(Math.random() * (max - min)) + min; } function game (n, repick) { var list = new Array(n); list.fill(0); // 0 - no prize var doorWithPrize = randRange(0, n); list[doorWithPrize] = 1; //put prize behind door var PickedDoorNumber = randRange(0, n); // initial door pick while(list.length > 2 && repick === true) { for(var i = 0, len = list.length; i < len; i++) { if(list[i] === 0 && i !== PickedDoorNumber) { // choose door without prise and not picked by player list.splice(i, 1); // open one door - reduce doors that we can pick now break; } } PickedDoorNumber = randRange(0, list.length); // pick new door from doors that left } return list[PickedDoorNumber] === 1; //win prize ? } function test (N, n) { console.log('start without repick') var result = []; for(var i = 0, len = N; i < len; i++ ) { result.push(game(n, false)); } var winnings = result.filter(function(itm){ return itm === true}); console.log('Win percent: ', (winnings.length / N).toFixed(4)); console.log('start with repick') var result = []; for(var i = 1, len = N; i <= len; i++ ) { result.push(game(n, true)); } var winnings = result.filter(function(itm){ return itm === true}); console.log('Win percent: ', (winnings.length / N).toFixed(4)); return 'done'; } test(10000, 3);
SelenIT3
28.10.2016 23:57+1PickedDoorNumber = randRange(0, list.length); // pick new door from doors that left
Вы тоже моделировали стратегию забывчивого игрока, т.е. в половине случаев даже после подсказки ведущего он у вас фактически сохраняет свой первоначальный выбор, а не меняет его.
а в changed у вас 66% тех которые вы не угадали, а не тех когда вы сменили выбор и угадали.
Вся суть задачи в том, что нет никакого «второго угадывания», а есть один случайный выбор и неслучайная возможность его инвертировать. Т.е., если игрок не угадал машину с первой попытки, то при инверсии выбора он получит ее гарантированно. Поэтому вероятность промахнуться первый раз и вероятность выиграть при смене выбора — это одна и та же вероятность.
drawwww
27.10.2016 08:26Получилось всё наоборот
c++#include <iostream> #include <cmath> using namespace std; int r13() { return (double)rand() / (double)RAND_MAX * (double)3; } #define REP 0 //Повторять выбор или нет int main() { cout << "STATUS\tPRIZE\tCHOOSE1\tDOOR1\tCHOOSE2\tDOOR2\tPERCENT\n"; int n = 0; int win = 0; while (true) { //SET PRIZE const int prize = r13(); //First choose int choose1 = r13(); int openDoor1 = r13(); while (openDoor1 == choose1 || openDoor1 == prize) openDoor1 = r13(); //Second choose int choose2; if (REP) choose2 = choose1; else { choose2 = r13(); while (choose2 == choose1 || choose2 == openDoor1) choose2 = r13(); } int openDoor2 = r13(); while (openDoor2 == choose2 || openDoor2 == openDoor1) openDoor2 = r13(); //Result win += (openDoor2 == prize) ? 1 : 0; cout << ((openDoor2 == prize) ? "WIN" : "LOOSE") << "\t" << prize << "\t" << choose1 << "\t" << openDoor1 << "\t" << choose2 << "\t" << openDoor2 << "\t" << (int)(100 * (double)win / (double)++n); cin.get(); } return 0; }alexkbs
27.10.2016 10:07Как вы объясните свой алгоритм? Вот попробуйте как здесь сделать.
drawwww
27.10.2016 18:151) Задаём случайным образом номер двери, за которой находится приз. -> prize
2) Выбираем случайно дверь. -> choose1
3) Открываем из двух оставшихся любую, за которой нет приза. -> openDoor1
Вариант 1:
4) Выбираем дверь, выбранную во 2 шаге. -> choose2 = choose1
Вариант 2:
4) Выбираем дверь, не выбранную во 2 шаге и не открытую в 3 шаге. -> choose2
5) Открываем ту дверь, которую не выбрал игрок и которую ещё не открывали. -> openDoor2
6) Анализ результатаDim0v
27.10.2016 22:485) Открываем ту дверь, которую не выбрал игрок и которую ещё не открывали. -> openDoor2
Зачем нам вообще эта дверь?
И почему выигрышем считается ситуация, когда приз оказался именно за этой никем не открытой и никем не выбранной дверью?
win += (openDoor2 == prize) ? 1 : 0;
Собственно, если заменить условие на
(choose2== prize)
чтобы выигрышем считалась ситуация, когда приз за той дверью, которую выбрали, то все встает на свои места и вероятности выводятся правильные.drawwww
27.10.2016 23:02Зачем нам вообще эта дверь?
После того как участник делал свой выбор, ведущий всегда открывал одну из оставшихся двух дверей, за которой, как он знал наперед, не было приза.
Или же во второй раз ведущий открывает именно ту дверь, на которую указал игрок?Dim0v
27.10.2016 23:11Ведущий открывает только одну дверь.
Т.е. ход игры такой:
1) Игрок выбирает дверь
2) Ведущий открывает одну из оставшихся дверей, за которой нет приза
3) Участник либо меняет дверь, либо не меняет
Все. Если за выбранной дверью приз — игрок выиграл. Если козел — проиграл.
3aicheg
28.10.2016 03:53+1Да вы переусложняете. Сгенерируйте два случайных числа — номер двери с призом и номер двери, выбранной игроком. Если числа равны — он выигрывает, не меняя свой выбор, x++. Если неравны — он выигрывает, меняя свой выбор, y++. Запустите цыкл на стопицот итераций, после чего сравните x с y.
3aicheg
27.10.2016 11:04Извините, что мне лень вникать глубже, но у вас, во-первых, функция r13() возвращает случайные числа 0, 1, 2, 3, а должна только 1, 2, 3, не?
drawwww
27.10.2016 17:51Да, верно. Но так получилось, что 3 почти никогда не появляется, поэтому на результат не влияет.
И всё же следует заменить r13 наreturn rand() % 3;
RussDragon
27.10.2016 22:11Простите меня, пожалуйста, что не в тему, но
return (double)rand() / (double)RAND_MAX * (double)3;
Что это? Зачем так усложнять? 0_oDim0v
27.10.2016 22:27Это для того, чтобы распределение равномерным оставалось. Если просто брать по модулю 3, то будет небольшой перекос в сторону нуля.
Например, если принять, что RAND_MAX равен 7 и rand() выдает числа, которые равномерно распределены на промежутке [0; RAND_MAX], то rand() % 5 будет давать числа 0, 1, 2, 3, 4 с вероятностями, соответственно, 2/8, 2/8, 2/8, 1/8, 1/8. Т.е. числа 0-2 будут появляться в 2 раза чаще, чем 3-4. И такая вот «нормализация» позволяет этого поведения избежать.
Хотя в рамках данной задачи, конечно же, это было совершенно не обязательно делать. Учитывая, что RAND_MAX как минимум на несколько порядков больше, чем 3 и, соответственно, эффект от такой нормализации вряд ли выйдет за рамки погрешности.SagePtr
29.10.2016 14:44Во-первых, делить не на RAND_MAX нужно, а как минимум, на (RAND_MAX+1).
Во-вторых, rand() всё равно возвращает дискретное значение, потому числа будут не равномерно генерироваться. Хотя и размазаны по диапазону будут более равномерно, чем в случае с остатком.
А именно, для 7 и 5 получится так:
[0, 0.625, 1.25, 1.875, 2.5, 3.125, 3.75, 4.375]
Или в вероятностях, 2/8, 2/8, 1/8, 2/8, 1/8
drawwww
27.10.2016 22:27Просто намешалось всё в голове с программирования в институте и вставил рандом для нецелых чисел, которые потом приводил к целым.
Выше уже привёл исправленный вариант.
trapwalker
29.10.2016 14:45Вот еще один вариант проверки на питоне. Может быть кому-то будет понятнее, но, ИМХО, совершенно понятно и интуитивно становится, когда переходим к 1000 дверей.
# -*- coding: UTF-8 -*- from random import choice total = 0 win_stay = 0 win_change = 0 win_random = 0 def test(n=3): doors = set(range(n)) # Множество всех дверей (n) car_in = choice(list(doors)) # Дверь, куда спрятана машина (случайная) my_choice1 = choice(list(doors)) # Мой первый выбор (случайный) doors_to_open = doors - {car_in, my_choice1} # Ведущий не может окрыть выбранную дверь и дверь с машиной while len(doors_to_open) > n - 2: # Ведущий открывает пустые двери, пока не откроет n - 2 двери doors_to_open.remove(choice(list(doors_to_open))) # пустые двери ведущий открывает произвольным образом closed_doors = doors - doors_to_open # Осталось закрыто только 2 двери (иначе не осталось бы выбора) my_choice_if_stay = my_choice1 # Мой выбор, если не меняю решение my_choice_if_change = list(closed_doors - {my_choice1})[0] # Мой выбор, если меняю my_choice_if_random = choice(list(closed_doors)) # Мой выбор, если выбирать случайную из оставшихся global total, win_stay, win_change, win_random # Дальше подсчитываем статистику total += 1 if my_choice_if_stay == car_in: win_stay += 1 if my_choice_if_change == car_in: win_change += 1 if my_choice_if_random == car_in: win_random += 1 for i in xrange(10**5): test(3) print('win_stay : {:10} {:.4}%'.format(win_stay , 100.0 * win_stay / total)) print('win_random: {:10} {:.4}%'.format(win_random, 100.0 * win_random / total)) print('win_change: {:10} {:.4}%'.format(win_change, 100.0 * win_change / total)) print('TOTAL : {:10} {:.2f}%'.format(total, 100.0))
Zolg
27.10.2016 01:21+3Пришло в голову еще одно абсолютно интуитивное решение: ведущий не открывает никакие двери, вы просто играете с ним в игру: кто угадал дверь, того и машина. Вы ходите первым, ведущий вторым. Но он ЗНАЕТ за какой именно дверью машина. Оцените шансы на выигрыш свои и его.
Grindok
27.10.2016 12:51Ну во-первых это не решение, а задача.
Ну и во-вторых одно из условий, что надо угадывать. В итоге ведущий никогда не выиграет. А мои шансы 1/3. Либо я угадаю с первого раза, либо все, конец игры.Zolg
27.10.2016 14:28+1Это эквивалентная задача, оставляющая меньше психологических метаний с открытием и обменом дверьми.
Под дверью, выбираемой ведущим, естественно понимается оставшаяся НЕ открытой.
Ведущий, знающий, где машина, может НЕ выиграть только в одном случае: если вы своим первым ходом угадали, где машина, лишив его какой-либо возможности выиграть на втором ходе. В остальных случаях он выберет (оставит НЕ открытой) именно дверь с машиной.
Barafu
27.10.2016 01:52-1Предвидя тусовку любителей теорвера, позвольте вопрос.
Предположим, что где-то на Земле бродит один динозавр, и будет бродить, пока его не найдут. Можно ли сказать, что средняя вероятность встретить динозавра для человека — один к семи миллиардам, или это так не работает?vics001
27.10.2016 02:21+1Конечно, не работает. Хотя я думаю отписаться выше, но все просто, есть «наивное» понимание вероятностей, из-за него и не было построено тервера до 20-го века, до Колмогорова. Теория вероятностей очень строгая мат. теория, которая никакого отношения к нашим рассуждениям о вероятности не имеет. Единственное, что приближает нас к реальности это мат. статистика, но там все гораздо сложнее.
К примеру, про вашего динозавра. Что такое верояность — мера на множестве событий. Что мы будем считать событием? И здесь уже первая проблема, вероятность в бесконечном множестве событий — мы живем бесконечно долго? а динозавр? ну предположим упростим, считаем вероятность встретить в этом году. Хорошо, но это не определяет множество событий. Сколько людей мы встретим в среднем в году? Предположим 1000 разных. Ок, можно сказать, что вероятность встретить… — формула с факториалами пересчитывающая 1000 комбинаций из 7 млрд, не включая одну.
И что мы получили? Получили некоторое число, которое никакого отношения к теории вероятностей не имеет. Почему, да потому, что мы что-то предпологали, что может быть абсолютно неверно, мы еще к тому же предположили, что вероятность встретить динозавра равно вероятности встретить индуса или китайца, что тоже может быть не верно и т.д. т.п. Так вот теория вероятности «работает» только тогда, когда можно эти предположения проверить на практике и посчитать функцию распределения и т.п., а для этого как раз и нужна мат. статистика. После этого, можно воспользоваться теорией вероятностей, но думаю большинству людей уже не пригодится, так как все можно и так посчитать.
Ivan22
27.10.2016 09:45-1работает, если уточнить условие. ПОСЛЕ того как динозавтра кто-либо встретит посчитаем вероятность что это будет именно этот Вася Пупкин — вот тут да, одна семимиллиардная.
Zolg
27.10.2016 14:33Тоже нет. Ведь динозавр не регулярно случайным образом телепортируется в случайную точку земного шара, а бродит по маленькому острову с населением в 100 человек и плавать не умеет.
Впрочем, даже если бы он телепортировался случайным образом, это бы тоже не работало.feodead
27.10.2016 22:17Нужно просто добавить условие.
Представим, что 7 миллиардов сферических людей в вакууме размазаны равномерным слоем по всей поверхности Земли. Динозавр телепортируется в случайную точку на поверхности Земли. Какова вероятность, что он телепортируется именно на вас?
rotor
27.10.2016 02:27Формулу расчета можно сильно упростить. Необходимость менять дверь легче объяснить по другому:
Если изначально принять стратегию выбора неправильной двери, то вы делаете свой выбор (выбираете неправильную дверь) с вероятностью2/3. После того, как одна из неправильных дверей открыта, вы не меняете свой выбор относительно неправильной двери и открываете единственно возможную при первоначальном выборе правильную дверь.
Suvitruf
27.10.2016 04:34Ведущий выбирает одну из коз и открывает её, если игрок выбрал другую дверь.
Не надо открывать коз )
vadimr
27.10.2016 05:24+7Поскольку авторы эксперимента не затруднилось объяснить голубям его условия, то голуби рассуждают, что результатом первого выбора является пропадание света, поэтому он ошибочен.
Errandir
29.10.2016 14:45Так, на сколько я понял, во втором эксперименте они переучились. Или там были другие голуби, а не те же самые?
lightman
27.10.2016 07:44+1Такой умозрительный вопрос: если утверждается, что для повышения вероятности нужно сменить дверь, почему смена двери на ту же самую не триггерит волшебное повышение вероятности?
Другими словами: представьте что после того как ведущий открыл одну дверь, у участника закружилась голова и он позабыл, какую дверь выбирал вначале и ткнул в одну из оставшихся двух наугад. В этом случае у него повысится шанс успеха или нет? А если он вновь выберет ту же самую дверь что и в начале?3aicheg
27.10.2016 08:16+6Изначально имеются три закрытые двери. Можно выбрать любую с вероятностью выигрыша 1/3. Вероятность проигрыша 2/3. Если бы вдруг после этого можно было сменить выбор и вместо уже выбранной двери выбрать оставшиеся две (ничего пока еще не открывая), вероятность выигрыша стала бы 2/3, а вероятность проигрыша — 1/3. По-сути, именно такой выбор, в несколько завуалированной форме (открыв одну из оставшихся дверей, за которой заведомо коза), и предлагает ведущий — представьте, что вы сперва выбрали дверь А, потом сменили выбор на пару дверей Б и В, после чего ведущий открыл невыигрышную дверь Б — по существу ничего не поменялось.
Если голова закружилась и заново выбрали одну из двух оставшихся закрытыми дверей — вероятность выигрыша 1/2, это выше, чем изначальная 1/3, но ниже, чем 2/3, если бы мы изменили выбор, ничего не забывая.Eldhenn
27.10.2016 15:34> Если бы вдруг после этого можно было сменить выбор и вместо уже выбранной двери выбрать оставшиеся две
Вероятность выигрыша стала бы 1, так как за одной из двух выбранных точно находится приз.3aicheg
27.10.2016 19:03Отчего же? Он либо за первой выбранной дверью с вероятностью 1/3, либо за оставшимися двумя с вероятностью 2/3.
sams0m
27.10.2016 10:09+1Все объясняют неправильно. Дело в том что вы отвлекаете своё внимание на блестяшку. А именно на дверь с призом, а вы считайте вероятность на пустые двери с учётом того что ведущий не может выбрать в качестве пустой вашу дверь. Учтя это всё становится на свои места.
paluke
27.10.2016 12:51+1Если участник вдруг забыл, какую дверь выбирал вначале — то вероятность выиграть у него — 1/2.
С вероятностью 1/2 он выберет ту же дверь что и в начале, за которой машина с вероятностью 1/3, и с вероятностью 1/2 — другую дверь, за которой машина с вероятностью 2/3. Суммируем: 1/2 * 1/3 + 1/2 * 2/3 = 1/2. Внезапно.
GokenTanmay
27.10.2016 12:51потому, что зная в какой паре дверей находится автомобиль с равной вероятностью из 1к3, ты выбираешь не одну дверь, пару против одной. (1/3+1/3) против 1/3… что лучше? а своим первоначальным выбором — ты фактически определил пару с общей вероятностью 2/3, которую выгоднее потом выбрать.
FirExpl
27.10.2016 12:51Данная ситуация равносильна обычному выбору из 2 дверей и вероятность равна 0.5 для каждой из дверей.
«почему смена двери на ту же самую не триггерит волшебное повышение вероятности?»
Может потому что смена двери на ту же самую не является сменой двери по определению?
Попробую разжевать другими словами:
1 шаг: выбираем любую дверь, очевидно (тут пока ещё действительно очевидно), что вероятность того, что мы ошиблись равна 2/3.
2 шаг: ведущий убирает неправильную дверь. Вероятность того, что мы ошиблись по прежнему равна 2/3! Возможно это самый контринтуитивный момент, но следует понимать, что информацию о том, какая конкретно из 2 других дверей неправильная ни коем образом не меняет нашу первоначальную оценку, т.к. мы и так знали, что как минимум 1 из них с козой.
3 шаг: вычисляем вероятность того, что смена двери приведёт к ошибке, 1 — 2/3(вероятность из шага1) == 1/3.
4 шаг: как мы помним из терверов, вероятность победы при смене двери это «1 — вероятность_поражения», т.е. вероятность победы 1 — 1/3 == 2/3. Ч.т.д.
3aicheg
28.10.2016 04:11Вот симуляция вашего варианта задачи с закружившейся головой: https://jsfiddle.net/8gsrx5zj/
Как видим, случайный перевыбор из двух оставшихся дверей не увеличивает шансов.3aicheg
28.10.2016 04:28Чего-то покорёжило в jsfiddle и он оставил там прежний вариант задачи, вот правильный: https://jsfiddle.net/8gsrx5zj/3/
Alert123
27.10.2016 08:27+2Если ты выбрал дверь, и тебе сразу не дали машину, разумеется надо менять выбор :)
Голуби руководствовались именно таким алгоритмом.
DimVasiliev
27.10.2016 08:27+6В передаче «Разрушители Легенд» экспериментально подтвердили всё выше написанное…
jok40
28.10.2016 09:15И Джерри и Адам, как я погляжу, довольно невезучие парни — чаще всего с первого захода не угадывали где приз. Поэтому и получился такой перекос.
3aicheg
28.10.2016 10:29Судя по многим их экспериментам, они просто не учили в школе математику с физикой. А ведь если бы старались, могли бы быть отличниками, а не богатыми и знаменитыми ведущими популярного шоу!
u010602
27.10.2016 08:27+4А по-моем голубей выдрессировали менять кормушку. Т.е клюнуть любую, потом другую. Т.е они не решали задачу угадать где корм. Они решали задачу — как нужно правильно клевать что-бы еду получать. И когда они клевали АА получали редко, когда АБ — часто. Аналогичный для человека опыт будет — запустить эмуляцию на компе и посмотреть в каком из вариантов приз выпадает чаще, без какого-либо анализа задачи и знания условий.
Например так можно было бы описать задачу, и человек бы тогда справился как и голубь
У вас три кнопки, вам нужно нажать любую, потом одна из кнопок исчезнет, вам нужно жать на одну из оставшихся двух. После вы получаете или не получаете приз. Вам нужно вычислить какой алгоритм поведения более результативен.knstqq
27.10.2016 08:52+7Тут и с людьми также сделали. Целый месяц просили выбрать дверь у одних и тех же людей.
С людьми вышло иначе. За 30 дней эксперимента некоторый прогресс вначале наблюдался, но выявить тенденцию не удалось.
Shifty_Fox
27.10.2016 15:39Я думаю все дело в мотивации. Голубь хотел кушать, для него было важно выбирать правильно. Для человека по сути это был просто эксперимент на интерес, если конечно за правильной дверью не лежали небезразличные деньги.
u010602
28.10.2016 04:57Вы немного не уловили суть моего комментария. Люди ошибались, потому что подходили к задачке логически, они ее анализировали заранее, как мне кажется. И получив изначально не верное решение — ему следовали. А голубь подходил эмпирически, не пытаясь наложить свой предыдущий опыт, или понять как устроены двери. Голубь изучил феномен и выбрал стратегию. А человек изначально попытался понять феномен исходя из правил, и изучал именно правила, а не эмпирические результаты.
Если у человека забрать данные для первичного анализа, думаю он вел бы себя как голубь. Т.е. в данном случае правила только сбивают с толку.
Farxial
27.10.2016 08:27+3Потому что голуби не имеют такого ЧСВ, как у людей, и не считают, что:
1. Их выбор априори правильный;
2. Их процесс выбора автомобиля-кормушки не будет прерван ведущим. Ведь после того как сделан первый выбор, важно следовать ему дальше. А если есть шанс ошибиться в 1-й раз, то с учётом правил проведения шоу можно подождать с выбором, а первый сделать от балды.
2.1. Не должны уточнять правила шоу перед тем как в нём участвовать.
Среда, в которой они живут, способствует выработке у них #2, как следствие они должны вырабатывать #2.1. С #1 чуть сложнее: они оценивают свои возможности более реально, но это так потому что им не мешает то же ЧСВ — у них нет иллюзий на свой счёт.
evgkan
27.10.2016 08:27+2Предложу, наверное, самое простое объяснение.
Варианты перечислены в формате «Выбор участника — результат после открытия двери ведущим»:
выбрана 1ая (правильная) дверь — останется еще одна неправильная,
выбрана 2ая (неправильная) дверь — останется еще одна правильная,
выбрана 3я (неправильная) дверь — останется еще одна правильная.
GAZ69
27.10.2016 08:27+1Что-то мне подсказывает, что голуби в отличие от человека не решали задачу расчета вероятности, а отлаживали последовательность действий, приводящих к желаемому результату. Поэтому утверждение заголовка- неверно.
shurupkirov
27.10.2016 09:03-2Эксперимент с голубями не идентичен проведению шоу.
Голубей тренировали 30 дней, т.е. каждый день один и тот же голубь n-раз в день (я не в курсе, как часто им надо есть) смотрел на лампочки и пытался не умереть с голода.
Человек же в данном шоу участвовал только один раз без возможности улучшения своей стратегии. Я думаю, если бы один человек участвовал в 10 играх подряд, то он бы точно также прекрасно решал данную задачуIvan22
27.10.2016 09:49-1Если бы людей тоже недельку не кормить — думаю результаты бы улучшились моментально!
arheops
27.10.2016 09:50+3Перечитайте. Людям тоже 30 раз давали выбрать, одним и тем же, каждый день.
shurupkirov
27.10.2016 09:56+2Людям давали выбрать машину или просто правильную дверь?
Если это вариант №2, то
В чем стимуляция зоны удовольствия участия в эксперименте у людей?
У голубей с этим все прекрасно — они за еду участвовали в этом, решалась их потребность выживания
arheops
27.10.2016 10:10+1А люди получают удовольствие от самого факта выигрыша. Вы не знали?
shurupkirov
27.10.2016 10:44Я очень хотел бы посмотреть на человека тыкающего на 1 из 3 кнопок 200 раз без стимула и спросить:
В чем соль, брат?
shurupkirov
27.10.2016 10:43Перечитал оригинал статьи, там указано что люди участвовали в серии из 200 испытаний разделенных на 4 блока по 50 в каждом
An experimental session consisted of a series of 200 trials organized into four blocks of 50
Ohar
27.10.2016 12:52Проблема в том, что люди участвовать-то участвовали, но машины не выигрывали.
А голубям еду давали.
Bessmertnii
27.10.2016 10:32С людьми вышло иначе. За 30 дней эксперимента некоторый прогресс вначале наблюдался, но выявить тенденцию не удалось.
TimsTims
27.10.2016 09:22Голуби могли считать, что клюют зерна, и после того как зерно склёванг, они меняют свой выбор на соседнее зерно…
Oxoron
27.10.2016 10:01Как-то 4 студента на конференции вспомнили эту задачку (в каком-то фильме она мелькала). Мы честно пытались найти верное решение, а потом один заявил «все, я запускаю Python IDE для тестов». Через пару минут прикидок как написать тест раздался одновременный вопль всех участников: «я понял!!!».
betsuni
27.10.2016 10:31-3Допустим, да, пусть будет так, как сказали выше:
Пусть у нас будет не 3 двери, а 1000. Вы выбрали одну. Ведущий открыл 998 дверей с козлами. Теперь у вас две двери. Теперь очевидно, что за другой дверью шанс намного выше, чем за первоначальной. Т.к. при первоначальном выборе ваши шансы были 1\1000.
Не за другой дверью шанс выше, а в _целом_ шанс выше. Он стал 1/2, даже если мы не сменим свой выбор.
Поэтому я до сих пор не понимаю как именно смена двери может увеличить шанс.Farxial
27.10.2016 11:38В случае с 1/2 нужно потратить на правильный выбор меньше энергии, чем в случае с 1/3.
betsuni
27.10.2016 11:52-2Так а зачем его менять? Вдруг я захотел поменять, а потом бац, и выбрал снова тут же дверь, которую я выбрал изначально. Что, из-за того, что я захотел _изменть_ свой выбор, а потом в итоге его _не изменил_, мой шанс повысился? Но, дверь-то все равно одна и та же.
А если этот огород не городить с «захотел выбрать другую дверь, а в итоге так и остановился на первоначальном выборе», то он останется прежним?Farxial
27.10.2016 12:19Если относиться к этому процессу как Вы, то никакой разницы нет. А если пытаться угадать, то чем больше дверей тем труднее.
Farxial
27.10.2016 13:04Простите, забыл уточнить (на самом деле я написал об этом в п. #2 своего 1-го комментария здесь, просто стоило скопировать сюда и переформулировать).
Это работает лучше всего, если 1-й выбор был сделан не серьёзно. Если же он был сделан серьёзно, то нет смысла менять его, а шанс выиграть не меняется т.к. не меняется сам выбор.
roboter
27.10.2016 11:47+1Чтобы понять я бы предложил такой вариант,
возьми лист в клеточку, пусть кто то другой загадает ячейку.
теперь пробуем отгадать, выбираем ячейку которую мы думаем что была загадана.
теперь тот кто загадывает закрашивает все ячейки кроме вашей и загаданной.
имеем поле с 2 ячейками у которой 1 на количество ячеек, у второй 1/2
тоже самое работает и с 3 дверьми хотя менее очевидно.
TonyaR
27.10.2016 12:49Ты относишься к открытию двери ведущим, как к случайному событию, но это по условию задачи не так.
Вот как вся логика выглядит вообще без формул.
1) (об этом ниже уже писал Bonart и, возможно, кто-то еще в комментариях выше) ты первым шагом выбираешь дверь, которую НЕ откроют. Вот тут приз может оказаться случайно
2) ведущий убирает одну дверь за которой точно нет приза, и это НЕ выбранная тобою дверь на первом шаге. То есть твоя дверь не стала лучше, ее не открыли только потому, что ты ее «забронировал». Она так и осталась случайной.
А вот почему ведущий не открыл другую дверь? ее-то никто не бронировал! Совпадение? — не думаю..)
3) Шаг 2 неслучайный, а шаг 1 случайный. Если об этом помнить, то ты поймешь, что оставшаяся дверь куда более перспективная.
SelenIT3
27.10.2016 12:491/2 — это шанс угадать. Но можно не гадать, а использовать логику и действие ведущего как подсказку.
Шанс угадать одну дверь из n равен 1/n. Соответственно, с вероятностью (n-1)/n машина за какой-то другой дверью. А поскольку по условию ведущий, если вы не попали в машину с первого раза, оставляет закрытой только дверь с ней, то во всех случаях, когда вы не угадали дверь с первого раза, машина окажется именно за этой оставшейся дверью.
losse_narmo
27.10.2016 12:49+1Потому что вы путаете 2 варианта:
1) открыли 998 дверей наугад и за всеми были козы
2) открыли именно те 998 дверей за которыми козы (зная наперед, что там козы)
ne_virus
27.10.2016 10:32Думается мне они просто научили голубей выбирать другую дверь после переключения света. Не до конца ясны детали экспериментов с людьми, но как то сомнительно выглядит, что взрослый вменяемый человек видя, что, грубо говоря, 2 раза из 3 приз за другой дверью за целый месяц не догадается выбирать ее…
Не имею достаточно знаний в области, что бы подвергать сомнению формулы и расчеты, но всё таки… Независимо от наших умозаключений факты таковы, что изначально за 1 дверью машина и за 2мя другими козлы. Выкрутасы ведущего несущественны — с тем же успехом можно откинуть 1 дверь еще до выбора, на результат и положение машины и козлов это не влияет. 3 двери закрыты из 3, 2 из 2 или вообще 10 из 10 — все равно их вероятности содержать приз равновесны.Ohar
27.10.2016 14:30+1как то сомнительно выглядит, что взрослый вменяемый человек видя, что, грубо говоря, 2 раза из 3 приз за другой дверью за целый месяц не догадается выбирать ее…
barker
27.10.2016 10:36+9Ну вот опять. Сколько бы ни видел упоминаний Монти Холла в интернете — всегда в каментах находятся люди, которые начинают спорить что это всё не так и бла бла. Чем руководствуются эти товарищи? Они реально считают, что здесь могут быть какие-то свои мнения на этот счёт? Это какая-то терминальная стадия упёртого невежества. Я даже ещё могу спор о боге понять, там хоть трактовки можно выдумать и о терминах можно поспорить. Но спор о основах математики и прочих 2+2 в голове просто не укладывается.
thatsme
27.10.2016 11:12Указанное в статье решение, верно только при условии, что Монти ВСЕГДА открывает дверь с козлом и никогда с машиной. Мне не знакомо это шоу, поэтому я понятия не имею, каким образом открывалась дверь (было-ли видно всем участникам события, что за дверью козёл?).
Машина за дверью 1. Вероятность угадать 1/3. Я загадываю 2. Монти открывает дверь 3 и показывает(!), что там козёл. У меня новая игра из 2-х дверей: 1,2 и вероятность выиграть 1/2.
Если Монти козла не показывает, то доподлинно не известно открывал-ли он дверь с машиной или козлом, и в новой игре вероятность та-же что и раньше 1/3.
Учитывая данные из статьи, делаю вывод, что Монти козла показывал!
Насколько я понял, проблема в том, что большинство людей не воспринимают 2-ую попытку как новую игру с повышенными шансами.
Так?barker
27.10.2016 11:17+2Указанное в статье решение, верно только при условии, что Монти ВСЕГДА открывает дверь с козлом и никогда с машиной.
Разумеется, это же по условию задачи так:После того как участник делал свой выбор, ведущий всегда открывал одну из оставшихся двух дверей, за которой, как он знал наперед, не было приза.
Конечно, он показывает что там козёл, точнее, как следствие из предыдущего это очевидно и так, даже если не показывать, т.к. ведущий всегда дверь с козлом открывает и одного отметает из выбора.
Если Монти козла не показывает, то доподлинно не известно открывал-ли он дверь с машиной или козлом, и в новой игре вероятность та-же что и раньше 1/3.
Всё именно так и есть, вы верно поняли. Если ведущий не дал информации, вероятность не изменилась. Но в вашем случае вообще задача ломается, конечно, т.к. может быть машины вообще уже нет, конечно. И нет её там именно с вероятностью 1/3, а за двумя другими дверями с вероятностью 1/3 и 1/3 какие-то призы, например, две козы.
3aicheg
28.10.2016 04:48https://jsfiddle.net/o4ohox0x/
Симуляция игры, когда Монти открывает одну из двух оставшихся дверей случайно. Если за дверью оказывается машина — мы проиграли. Если я ничего не накосячил, то получается, что с равной вероятностью распределяются три исхода: 1. выиграли, если не меняли выбор, 2. выиграли, если меняли выбор, 3. проиграли, потому что не угадали с первой попытки, а ведущий «угадал».
arvitaly
27.10.2016 11:21+1Спор из-за терминологии, к математике отношения не имеющей, у нас не просто двери и козлы, у нас есть открытая дверь, закрытая дверь и выбранная дверь и изменение выбора (из-за него приходится вводить «выбранную дверь»). А задача описывается «посчитать вероятность двух оставшихся дверей». Поэтому и появляется желание связать 2 события и в логике замечается классическая ошибка «орел-решка» (когда вероятность не меняется).
Здесь события тоже математически не связаны, здесь вводится новая переменная. Этим и пользуется передача, в ней то двери остаются дверьми. Голуби же слов не используют, им проще.
А чтобы человек сразу начал верить и разбираться, лучший способ, имхо, следующий пример:
1. Допустим у нас 9 попыток, и автомобиль первые 3 раза в первой двери, вторые во второй третьи в третьей.
2. Допустим мы всегда выбираем 1 вариант и не меняем его
3. Тогда мы выиграем 3 раза
4. Допустим вы всегда выбираем 1 вариант и всегда меняем его
5. Тогда мы выиграем 6 разfawor1t
27.10.2016 12:48А если выбирать 1 и 2 дверь по очереди, то угадаем 5/9 что близится к 50/50, все никак не могу вникнуть почему при открытии двери ведущим, вероятность что та дверь которую не выбрал ни я ни ведущий выше той, которую выбрал я.Если нам доподлинно известно что во время выбора козы и автомобили местами не менялись)
fawor1t
27.10.2016 12:53Хотя логику я понял, на 9 попыток вероятность при смене выбора действительно выше.НО если как в шоу попытка всего одна, то разве вероятность не остается 50 на 50?
Shifty_Fox
27.10.2016 15:45Если в 1 случае из 1000 вы наступили в лужу при выходе из дома, от того, что кто-то выходит из той же двери всего один раз в жизни, вероятность его наступить в лужу не станет вдруг 50\50, она останется 1\1000, хоть и интуитивно кажется, что человек в итоге либо наступит, либо нет.
Смотрите на это так — люди в шоу, которые не меняли дверь, выигрывали в 1\3 случаях, люди которые меняли дверь выигрывали в 2\3 случаях. В какой из этих двух групп людей вы желаете оказаться?
ChiefPilot
27.10.2016 16:50Люди спорят, видимо, не с математикой, а рассказывают о том, что говорит интуиция. Я вот, например, смотрел на табличку в Википедии по этой теме и вижу, что математически всё правильно, а интуитивно никак не могу понять: как же это так, что на вероятность (на вероятность!) влияет то — помню я или не помню, какую из двух оставшихся неоткрытыми дверей я выбрал перед открытием (варинат с «закружилась голова и я забыл, какую выбрал»)…
barker
27.10.2016 18:16+1Не, они всегда уверенно рассказывают что вероятность будет 1/2. Потому что две двери же. А раз две двери, то 1/2. Это всё что им надо знать о тервере.
barker
27.10.2016 18:23как же это так, что на вероятность (на вероятность!) влияет то — помню я или не помню, какую из двух оставшихся неоткрытыми дверей я выбрал перед открытием (варинат с «закружилась голова и я забыл, какую выбрал»)…
Неважно помните вы или не помните! Важно чтобы вы поменяли дверь. Вы тут вообще ни при чём, за вас сделал активные действия ведущий и увеличил шанс приза за одной из дверью. Просто если вы «не помните» какую вы выбирали, вы не можете поменять дверь, очевидно, т.к. вы не в курсе какой был выбор до этого. Если вы «не помните», для вас подсказка ведущего потеряна, т.к. подсказка эта фактически «за дверью которую я не открыл вероятность приза повышена». Потому если вы не помните из каких двух дверей он выбирал, то для вас подсказка потеряна. НО для стороннего наблюдателя, например зрителя из зала который не терял память, разумеется, вероятность повышенная за конкретной дверью осталась очевидной. Вероятность не менялась, просто вы её сейчас не можете вычислить. Для вас эксперимент начался заново.
Bonart
27.10.2016 11:34+2Можно легко определить правильный ответ: выбрав одну дверь и сменив ее после подсказки ведущего игрок на самом деле принял решение НЕ открывать одну (выбранную изначально) дверь. Вторую открывает ведущий, а третью — он сам.
volkoff_roman
27.10.2016 12:48-1Возможно я невнимательно прочитал. А над людьми провели обучающий эксперимент? Такой как над шестью голубями.
В жизни ведь такую задачу редко кто решает. И участники постоянно разные.
shadovv76
27.10.2016 12:48+3по моему здесь довольно ясно просматривается такое объяснение.
смена выбора равносильна начальному праву открыть две двери.barker
27.10.2016 13:39+2по моему здесь довольно ясно просматривается такое объяснение.
смена выбора равносильна начальному праву открыть две двери.
Кстати, очень хорошее замечание. Но слишком тонкое, то есть понять «это почему это так» не проще, имхо, чем просто понять изначальное объяснение задачи)
Вот со ста дверями нагляднее ваше объяснение получается: изначально Я одну дверь могу открыть, выбираю одну из ста. У ведущего остаётся 99 дверей в ведении, которые ОН может открыть. Он берёт открывает 98 дверей (пока даже неважно что там за ними, хотя в конце мы вернёмся сюда и учтём что среди них обязательно нет приза). Теперь у нас остаётся выбор: остаться со своей «одной дверью», или присоединиться к открыванию «99 дверей ведущего»… открыв последнюю и помня, что в открытых до этого 98-ми приза не было. По-моему тут уже всем должно быть очевидно, что выгоднее быть среди тех, кто открывает 99 дверей, чем среди тех, кто открывает одну.
з.ы. И да, к чем это я… что «смена двери равна изначальному выбору открывать 99 дверей вместе с ведущим [учитывая то, что ведущий осознанно не забирает приз своим выбором]».
eversyt
27.10.2016 12:49мне кажется тест с голубями не корректен. они могут тыкать в двери наугад. в одну не получилось (загорается лампочка) и они тыкают в другую. т.е. голубь изначально находит случайно верную стратегию и ее использует. человек считает что вероятности равны и использует неправильную стратегию. и ей следует
dimonkin
27.10.2016 14:42+1Чтобы интуитивно почувствовать в чем суть, сделал следующее:
1. Представил 1 000 000 000 дверей.
2. 999 999 998 дверей было открыто
3. Интуитивно понятно, что слишком маловероятно, чтобы первый выбор был удачным.betsuni
27.10.2016 15:00-1Да, но с каждой открытой дверью ваши шансы увеличиваются _сами по себе_.
> 3. Интуитивно понятно, что слишком маловероятно, чтобы первый выбор был удачным.
Почему? Был шанс 1 к миллиону и стал один к 2 когда отрыли 999 999 998 дверей.TonyaR
27.10.2016 15:36+1betsuni, попробую еще раз обратить твое внимание на то, что:
1) ты в первый раз выбираешь дверь случайно
2) ведущий после твоего «хода» открывает двери осознанно. Он точно знает, что за ними нет приза
2) он не откроет дверь, которую ты изначально выбрал, только потому, что ты ее ранее своим выбором «забронировал»
В случае с миллионом это и правда особенно наглядно. Он открыл 999 999 998 дверей, при этом не тронул только две. Причин у него не открывать тоже только две: или твоя бронь (случайная дверь 1 из 1 000 000 000), или тот факт, что за дверью приз. Ты точно не захочешь поменять свой выбор?TonyaR
27.10.2016 15:47неосторожно выразилась в пункте 2). Правильнее так:
он не откроет дверь, которую ты изначально выбрал, как минимум уже только потому, что ты ее ранее своим выбором «забронировал»jok40
27.10.2016 16:58Один с девятью нулями — это миллиард. Но это я так, к слову — не обращайте внимания. А по теме — Ваше объяснение мне очень понравилось. Да, пожалуй, в этом случае я поменяю дверь не раздумывая ни секунды.
betsuni
27.10.2016 18:46-21) а как можно выбрать дверь неслучайно?
3) ну и что что «только» или «как минимум уже только потому»?
поменяю ли, или не поменяю — осталось двери 2. вероятность стала 1/2 автоматически
вон saroff объяснил.jok40
27.10.2016 19:15+1Внимательно перечитайте абзац, идущий после пункта 3.
По теме:
- вероятность того, что Вы ткнули пальцем в кучу из миллиарда дверей и сразу угадали правильно — практически равна нулю
- на основании каких умозаключений Вы вдруг решили что Ваша везучесть, после действий ведущего, увеличилась с нуля до одной второй?
betsuni
27.10.2016 19:49>на основании каких умозаключений Вы вдруг решили что Ваша везучесть, после действий ведущего, увеличилась с нуля до одной второй?
потому, что осталось 2 двери — моя и еще одна.jok40
27.10.2016 20:05Именно в этом Ваша ошибка: Вы выбирали одну дверь из миллиарда. И вероятность того, что приз за этой дверью всегда останется одна миллиардная — вне зависимости от действий ведущего.
Представьте себе несколько изменённую последовательность действий:
- Вы ткнули пальцем в кучу из миллиарда дверей
- Вам позволили тут же открыть эту дверь
- Ведущий открыл 999 999 998 оставшихся дверей и одну дверь оставил закрытой
Всё ещё считаете, что Ваша везучесть после действий ведущего увеличилась до одной второй?betsuni
28.10.2016 05:47ну вроде как да.
jok40
28.10.2016 07:44Ну вроде как нет. Уже на шаге два Вы увидите за своей дверью козла — с практически стопроцентной вероятностью. И что бы потом не делал ведущий — пел, плясал, ходил на руках, стучал в бубен, открывал миллиард других дверей или просто ушёл спать — за выбранной Вами дверью будет стоять козёл.
betsuni
28.10.2016 10:29>Уже на шаге два Вы увидите за своей дверью козла
почему?jok40
28.10.2016 10:38Если цитируете чужие фразы, то делайте это полностью — не вырывайте, пожалуйста, куски из контекста. Я сказал так:
Уже на шаге два Вы увидите за своей дверью козла — с практически стопроцентной вероятностью.
Отвечаю на Ваш вопрос «почему»: потому что на шаге один Вы стоите перед миллиардом закрытых дверей. За 999 999 999 из них стоят козлы и только за одной — автомобиль.
TonyaR
27.10.2016 19:28+11) Выбрать дверь неслучайно можно в том случае, если ты знаешь, что за ней. Именно так и выбирает двери ведущий
2) Причины неслучайного выбора ведущего очень важны. Ведущий не открывает а) дверь, которую выбрал ты (уже только поэтому она точно останется закрытой) и b) дверь, за которой есть приз.
Тебе просто нужно помнить, в каких условиях ты принимаешь первое решение. Да, ты гарантируешь одной случайной двери из миллиарда «выход в финал». Но вероятность того, что за ней приз так и останется одной из миллиарда.
saroff
27.10.2016 15:44Вы не правильно понимаете порядок действий, он такой:
1. Есть миллион дверей. Вы выбираете одну — шанс, что эта дверь верна 1 к миллиону.
2. Ведущий открывает 999 998 неверный дверей.
3. За одной из двух оставшихся выбор точно есть приз.
(3.5) Вы можете поменять свой выбор на вторую не открытую дверь.
4. Вы узнаете результат.
Заметьте, если вы не меняете свой выбор, то шаги 2-3.5 никак не влияют и вообще могут быть опущены. Представьте что вы сделали выбор и ушли в туалет пока ведущий открывал другие двери. Т.е. шанс остается 1 к миллиону.
Чтобы шанс был 1 к 2, порядок действий должен быть:
1. Есть миллион дверей.
2. Ведущий закрывает 999 998 дверей, в которых точно нет приза.
3. Вы выбираете из 2 оставшихся.
В таком случае нам вообще не важно сколько дверей изначально, шанс всегда 1 к 2.Eldhenn
28.10.2016 11:11> Представьте что вы сделали выбор и ушли в туалет пока ведущий открывал другие двери
А теперь представьте, что вы не ушли в туалет, а остались на сцене. И после открытия каждой двери каждый раз напряжённо размышляли по полчаса — и результатом размышлений оказывался выбор (новый выбор!) той же двери, что была выбрана на предыдущем шаге.
В чём разница?saroff
28.10.2016 11:21Вот именно, разницы нету. Пока вы сидели в туалете, вы не делали никакого нового выбора, просто вернулись и зарбали то что было за вашей дверью. Если вы решили остаться со своим выбором — не важно, смотрели ли вы, как ведущий открывает другие двери, не смотрели, решали, не решали, это все равно что вы выбрали дверь и сразу открыли ее.
Toshiro
27.10.2016 15:15+1Чего я не могу понять — так это на основании чего постулируется допущение, что 1/3 вероятности выигрыша, которую имела открытая ведущим дверь, переходит не к той двери, что я выбрал. Почему не у выбранной мной двери становится 2/3?
SelenIT3
27.10.2016 15:28Вероятность 2/3 изначально была у того, что машина за какой-то из дверей, которые вы не выбрали. И неслучайно открывая дверь без машины, ведущий невольно показывает вам, за какой именно.
Toshiro
27.10.2016 18:13-2Вы не ответили на вопрос. Изначально мы знаем что раз ведущий откроет одну из двух козлодверей, мы можем допустить что у одной из оставшихся вероятность 2/3 — но почему именно у не той, которую выбрал я изначально?
Почему выбранная мной дверь автоматически козлодверь?barker
27.10.2016 18:18Выше множество тредов, с выкладками и разносторонними аналогиями и моделями, после которых уже несколько людей сказали «спасибо я всё понял». Зачем вы спрашиваете заново одно и то же)
Toshiro
27.10.2016 19:21-4То есть внятного и точного ответа нет, и это все из области мошенничества, а не математики. Спасибо, я все понял.
saroff
27.10.2016 19:30Много раз объясняли, что шанс того, что вы выбрали изначально правильную дверь — 1\3. Шанс, что правильная дверь, это одна из других — 2\3. После того, как ведущий открыл одну из других дверей, шанс для вашей двери все еще остался 1\3. Шанс того, что автомобиль находится за одной из двух других дверей — 2\3. Ведущий открывает одну из других дверей, которая заведомо неверная. У нас есть две двери, шанс того, что автомобиль за одной из них 2/3, одна из них открыта, и мы знаем, что автомобиля за ней нету. Но шанс 2\3 никуда не девается.
С шансом за нашей дверью тоже ничего становится, если мы не изменим свой выбор, то вообще не обязательно открывать другую дверь, можно сразу открыть нашу, и шанс 1\3.
saroff
27.10.2016 19:32Грубо говоря, если мы меняем свой выбор, то мы вместо нашей двери, идем и открываем 2 другие двери. Открыв две двери шанс ведь больше чем открыв одну? Просто в изначальном условии ведущий нам помогает открыть одну дверь :)
SelenIT3
27.10.2016 19:54+1Дверь, которую выбрали вы, ведущий по условию не открывает никогда. Машинодверь — тоже.
Далее варианты:
1) Вы указали на машинодверь. Ведущий может открыть любую из двух козлодверей, останется вторая козлодверь. Менять выбор вам невыгодно.
2) Вы указали на козлодверь. Ведущий может открыть только одну дверь (вторую козлодверь), останется машинодверь. Менять выбор вам выгодно.
Как соотносятся вероятности этих вариантов?Toshiro
28.10.2016 03:04-3Они эквивалентны, т.к. в действиях ведущего нет указания на то, козлодверь я выбрал или машинодверь. Я мог бы рассудить статистически, если бы перед финальным выбором мне дали 100 симуляций. Но у меня только 1 попытка.
FirExpl
28.10.2016 10:42Пусть d1, d2, d3 — это номера дверей, где d1 != d2 != d3, и все они принадлежат множеству {1, 2, 3}
f(d) — функция, которая возвращает true, если за дверью с номером d находится приз, и false если там козёл
P — функция вероятности успешности события, возвращает число из отрезка рациональных чисел [0..1]
1) Игрок выбирает номер двери из {d1, d2, d3}. Пусть игрок выбрал номер d1
2) P( f(d1) == true ) == 1/3 (тут вроде вопросов ни у кого нет)
3) P( f(d2) == true || f(d3) == true) == 1 — P( f(d1) == true) == 1 — 1/3 == 2/3. Это базовые знания теории вероятностей, если данный момент не ясен, то продолжать разбираться в этом парадоксе нет смысла, надо повышать свою образованность в данном разделе математики.
4) Ведущий открывает одну из невыбранных дверей, за которой находится коза. Пусть он открывает дверь d2.
5) Из предыдущего пункта следует, что f(d2) == false.
А теперь, внимание, магия
6) P( f(d2) == true || f(d3) == true) == P ( false == true || f (d3) == true) == P ( f(d3) == true)
Как мы помним из пункта №3, P( f(d2) == true || f(d3) == true) == 2/3, а следовательно
P (f(d3) == true) == 2/3
7) В результате мы имеем, что вероятность выиграть оставив дверь d1 равна 1/3
А вероятность выиграть сменив выбор на d3 равна 2/3
SelenIT3
28.10.2016 12:16+1По такой логике, шанс выиграть в любую лотерею — 50%. В действиях продавца билета ведь тоже нет указания, выигрышный билет вы взяли или нет, а значит, вероятности этих вариантов «эквивалентны»?
Или нет? И всё-таки можно оценить априорную вероятность и для единичного выбора?Toshiro
28.10.2016 20:46-1Хуже, по такой логике в любой ситуации смена выбора имеет большую вероятность везения. Т.е. догма что выбранная мной дверь должна быть всегда проигрышной постулирует, что я ВСЕГДА должен менять выбор. Это некорректно ни математически, ни с точки зрения физического смысла процесса. Короче треш. Но народ как видите верит. Easy money)) Эдвард Бернес апплодирует стоя))
SelenIT3
28.10.2016 23:34догма что выбранная мной дверь должна быть всегда проигрышной
существует только в вашем воображении.
Ни одна стратегия (всегда стоять на своем, всегда менять, пытаться снова угадать, бросить монетку, попросить помощи у зала, позвонить другу...) не дает гарантии выигрыша. Вопрос задачи лишь в том, при какой стратегии априорная вероятность вашего выигрыша выше. Не спорю, выбрать математически верную стратегию и всё равно с вероятностью 1/3 проиграть — это обидно, но, имхо, собственными руками увеличить вероятность собственного проигрыша в полтора-два раза — еще обиднее…Toshiro
29.10.2016 17:39-2В том и дело, что это увеличение проигрыша своими руками — существует только в вашем воображении. Просто вы решили так интерпретировать математику, в которой нет точного обоснования одного из условий.
SelenIT3
29.10.2016 22:26+1Простите, точного обоснования какого из условий вам не хватает? Вы не согласны с тем, что априорная вероятность нахождения машины за одной дверью из трех меньше априорной вероятности ее нахождения за двумя оставшимися дверьми?
saroff
27.10.2016 15:27В качестве варианта объяснения, почему при смене выбора вы будете выигрывать чаще, можно представить условия немножко по другому, вам дается на выбор два варианта:
1. Вместо варианта, когда вы не изменяете свой выбор, вы просто выбираете одну дверь, и ведущий сразу сообщает вам выиграли вы или нет.
2. Вместо варианта, когда вы изменяете свой первоначальный выбор, вы можете выбрать сразу две двери, если хотя бы за одной из них будет приз — вы выиграли.
Очевидно что при втором варианте вероятность выиграть в два раза больше. Такая аналогия верна, потому что после первоначального выбора ведущий говорит вам, в какой из других двух дверей точно нету приза, т.е. если мы изменим выбор, это равносильно тому, что мы изначально выбрали сразу две двери.betsuni
27.10.2016 18:53интересно объясняете, я почти понял
1. выбрать одну из скольки? из 3х? или из 2х?
2. тот же вопрос: выбрать 2 из скольки? и почему именно так: если хотя бы за одной из этих 2ух дверей....? вы ведь также выиграете, если только за одной из них будет приз.saroff
27.10.2016 19:23В обоих случаях выбираем из трех.
Чтобы было легче объяснить, представим что дверей не 3, а 100. Так вот, помните, после нашего выбора, ведущий откроет 98 дверей, которые точно не содержат приз, если мы изменим свой выбор, и в этой двери окажется приз, то это мы можем думать, что мы сразу выбрали 99 дверей и открыли их все, если в одной из них был приз, то выиграли.
Т.е. если мы не меняем выбор, это все равно что мы выбрали 1 дверь из 100 и сразу ее открыли.
Если мы изменили выбор, это все равно что мы выбрали 99 дверей из 100 и открыли их все.betsuni
28.10.2016 10:36не вижу логики снова.
что именно повышает наш нас выиграть? то, что мы меняем свой выбор? а если тогда сделать так: ведущий откроет 98 или даже 97 дверей, мы скажем: хммм, дайте подумать, выбираю дверь… какова тут вероятность выигрыша? 1/3. верно? двери ведь осталось 3 и выбираем одну из них. и среди них наша первоначальная дверь.
внимание. верояность 1/3 __даже если__ мы передумаем менять свой первоначальный выбор. так что именно повышает наш с 1/100 до 1/3? само желание выбрать какую-то из оставшихся 3х дверей? но, ведь мы снова может выбрать первоначальную. таким образом, не меняя свою дверь мы повысили шанс с 1/100 до 1/3. мы можем вообще даже не изъявлять желание менять свой выбор. логично?saroff
28.10.2016 10:57+1Есть 100 дверей, если мы выбираем одну, шанс выиграть 1/100. При этом открывает ведущий другие двери или нет, это абсолютно никак не влияет на наш шанс выиграть, он все еще 1/100.
Представьте, что вместо дверей у нас есть мешок, в нем 100 шариков, 99 пустые, в 1 приз. Мы наугад вытягиваем из мешка 1 шарик и забираем его себе. Какой шанс что он верен? 1/100. Если ведущий сейчас вытащит из мешка 98 не верных шариков и оставит там только один. Как изменится наш шанс на то, что шарик в нашей руке верен? Да никак, мы вытягивали наш шарик когда в мешке было 100, и не важно что после этого ведущий сделает, шанс всегда останется 1/100. Ведь если мы не меняем выбор, то это именно так, мы оставляем себе шарик который с шансом 1/100 верен. Мы не выбираем второй раз. Для того чтобы шанс изменился на 1/2, нам нужно было бы положить свой шарик обратно в мешок, перемешать, и потом наугад из них выбрать 1, Не зная какой мы выбрали изначально.
Каков же шанс, что после нашего выбора в мешке остался верный шарик? 99/100. После этого ведущий убирает из мешка 98 не верных шариков. Есть 2 возможных причины, почему именно этот один шарик остался в мешке 1 — Этот шарик верный. 2 — Верный шарик у нас в руке, но ведущий уже вытащил 98, и не может вытащить последний.
Чтобы произошло второе событие, при котором нам выгоднее придерживаться нашего выбора, нужно, чтобы изначально, с шансом 1/100 мы выбрали верный шарик.
При этом чтобы произошло первое событие, при котором нам выгоднее сменить выбор, нужно чтобы когда мы забирали один шарик из мешка, мы с шансом 99/100 забрали не верный, а верный остался среди прочих лежать в мешке.
Повторюсь, то, что ведущий что-то делает с остальными вариантами, когда мы уже выбрали свой, никак не может повлиять на вероятность уже выбранного нами варианта. Не изменяя свой выбор, мы не совершаем выбор второй раз с новым шансом, мы оставляем себе первоначальный выбор с тем шансом, с каким мы его доставали. Повторюсь, представьте что вы достали шарик из мешка и забрали его себе. Ведущий вынимает из мешка 98 не верных шариков и берет себе последний оставшийся шарик. После чего предлагает вам обменяться с ним шариками. Эти действия никак не могут повлиять на шанс верности шарика у вас в руке (1/100). И точно также они не влияют на шанс верности шарика в руке у ведущего (99/100), потому что именно с такой вероятностью мы, доставая свой шарик, оставили верный в мешке.Eldhenn
28.10.2016 11:07> то, что ведущий что-то делает с остальными вариантами, когда мы уже выбрали свой, никак не может повлиять на вероятность уже выбранного нами варианта
Правильно, потому что выбор уже свершился, он в прошлом, и вероятность его 1/100 была, есть и будет.
А в следующей итерации НОВЫЙ выбор. Из НОВЫХ дверей. Которых 99, а в пределе — две. Мы не можем выбрать открытые двери — так каким образом они участвуют в этом выборе?saroff
28.10.2016 11:17+1Нету нового выбора. Вспомните мою аналогию с шариками.
У нас есть шарик в руке. Мы выбирали его с вероятностью 1/100. Это было в прошлом и никогда не изменится.
После этого ведущий убирает из мешка 98 не верных вариантов и забирает себе последний оставшийся. Шанс, что мы оставили в мешке верный шарик — 99/100. Т.е. это шанс, что шарик в руке у ведущего верен. С этим шансом тоже никогда ничего не случится.
Теперь мы можем оставить себе наш шарик, с верностью 1/100, или поменять его на шарик ведущего, с верностью 99/100. Мы не делаем слепой выбор между двумя шариками, как в первом случае.
saroff
28.10.2016 11:19+1По другому говоря — мы делим шарики на группы. В первой группе 1 шарик, а во второй 99. Делим случайным образом. И ведущий нам говорит, что если вы выберете группу, в которой 99 шариков, то я уберу из нее 98 не верных и оставлю вам последний. Ясно ведь, что шанс, что верный шарик среди 99 шариков, больше чем это единственный в отдельной группе?
saroff
28.10.2016 11:33Т.е. мы распределяем все шансы, когда делаем свой выбор в первый раз. Как я говорил, случайным образом, делим на группы. Скажем что мы делим на группы не 1-99, а 10-50-40. И изначально можем выбрать себе только группу с 10. А потом ведущий убирает из всех трех групп не верные шары и оставляет только один, после чего мы можем спокойно поменять группу. Логично ведь, что там, где было 50 шаров, гораздо больше шанс, что оставшийся последний это верный, чем там где было 10?
Gearbeast
27.10.2016 15:37+1Насколько я понял, считать нужно так: 1/3 — дверь (первая сущность), которую выбрал ты, 2/3 — две оставшиеся двери (вторая сущность).
Далее ведущий открывает одну из 2х дверей. Шанс выигрыша у второй сущности остается 2/3.
В большом количестве повторений шанс у второй сущности естественно выше.
Не много легче понять, если рассматривать 2, не выбранные участником, двери, как единое целое.
Не много перемоделируем — есть 3 (а, б, в) двери за одной из них что-то есть. Шансы примерно равны — один к трем (33.3%). Как Вы думаете у двух дверей какой шанс? — примерно 66% или два к трем. И во втором туре Вы и оказываетесь в ситуации, где одна дверь против двух, одна из которых открытая.
Это нужно отделить от дверей и решать как математическую задачу (абстрактно).
640509-040147
27.10.2016 22:18Вроде бы простая задачка, но до меня дошло только после получаса вдумчивого чтения и активного мыслительного процесса.
maDik_Mak
27.10.2016 22:19С толку сбивает то, что дверь с призом откроется в самом конце, а Тервер при подсчетах вероятностей учитывает, что призовая дверь может открыться раньше. Что не происходит в данном случае.
По этому чтобы выиграть нужно в предыдущем шаге указать на НЕ ПРАВИЛЬНУЮ дверь (без приза). Во все предыдущие шаги нет разницы, выбираешь ты дверь с призом или нет. В примере с 3 дверьми шанс выиграть, при такой стратегии, будет 2/3. Если будет 10 дверей и на следующем шаге уберут 8 -то при такой стратегии шанс выиграть будет 9/10
Caullerd
27.10.2016 22:20Плюнул, написал код для игры со сменой выбранной двери и без смены, запустил по 10 раз сессии по 100 игр:
Всегда меняем свой первоначальный выбор:
Выигрышей: 60/100
Выигрышей: 58/100
Выигрышей: 59/100
Выигрышей: 68/100
Выигрышей: 59/100
Выигрышей: 64/100
Выигрышей: 62/100
Выигрышей: 60/100
Выигрышей: 57/100
Выигрышей: 57/100
Всегда настаиваем на первоначальном выборе:
Выигрышей: 26/100
Выигрышей: 29/100
Выигрышей: 43/100
Выигрышей: 41/100
Выигрышей: 37/100
Выигрышей: 38/100
Выигрышей: 42/100
Выигрышей: 40/100
Выигрышей: 40/100
Выигрышей: 34/100
3aicheg
28.10.2016 05:42Попытался систематизировать альтернативные формулировки задачи («а что если игрок забудет», «а что если ведущий не знает» и т. п.), приведенные в комментариях и написать симуляторы для каждой формулировки. Вот что получилось. Возможны, впрочем, ошибки в коде, сводящие все усилия на нет.
Классическая формулировка: игрок выбирает одну из трёх дверей, ведущий выбирает заведомо проигрышную из двух оставшихся, игрок может сменить выбор, либо не менять:
https://jsfiddle.net/rmbzhona/
Игрок с амнезией: выбирает одну из дверей, ведущий выбирает заведомо проигрышную из двух оставшихся, игрок тут же забывает вообще всё и заново делает выбор из двух еще не открытых дверей:
https://jsfiddle.net/8gsrx5zj/3/
Всё как в классической формулировке, но ведущий не знает, где машина — открывает случайно одну из дверей, не выбранных игроком. Там может оказаться машина, в этом случае игрок автоматически проигрывает:
https://jsfiddle.net/o4ohox0x/1/
Как в предыдущем варианте, но ведущий случайно открывает любую из всех трёх дверей — если за ней машина, игрок выигрывает, если выбрал эту дверь, проигрывает в противном случае. Если за ней машины нет, игрок может изменить выбор. Если ведущий открыл ту же дверь, что и игрок, и за ней нет машины — предполагаем, что игрок не идиот и меняет выбор автоматически, при этом ему надо выбрать вслепую одну из оставшихся двух дверей. Не уверен в корректности формулировки, т. е., правильно ли сводить воедино смену выбора «вслепую» и смену выбора, когда игрок видит, что изначальный выбор был неверен, но тем не менее:
https://jsfiddle.net/vLsrbfvp/1/
Как видим, для классической формулировки смена изначального выбора значительно увеличивает вероятность выигрыша. Для остальных формулировок ничего не меняется — примерно поровну распределяется вероятность выиграть, сменив выбор, выиграть, не меняя выбор и проиграть в любом случае.
habra_sultan
28.10.2016 20:32-1тоже долго не мог понять да как так ну 50/50 же (интуитивно);
для себя как для интутивного человека разбил ситуацию для понимания интуитивно:)
берем пример с 1000(уже упоминавшийся тут много раз)
и вот из этих 1000 делам выбор.
чисто интуитивно (и фактический) маловероятно что тыкнем в нужную нам дверь.
потом убирают 998(любой из которых запросто мог быть и нашим выбором просто наш другой и его не убирают)
теперь осталось 2 помня что скорее всего мы выбирая из 1000 ошиблись, то другой из 2х более вероятно нужный.
Ведущий хоть и не предвзятый актом убирания остальных вариантов как бы намекает ваш вариант такойже никчемный как остальные 998.
quartz64
28.10.2016 22:35Тут стоит отделить психологический фактор (предрассудок «от добра добра не ищут») с попаданием в логическую ловушку, когда мы видим, что дверей осталось две и решаем, что вероятность получить приз в первоначально выбранной двери равен 1/2, забывая, что в изначальном состоянии вероятность составляла 1/3. Если мы будем стирать игроку память после убирания двери, то получим родственный «парадокс Спящей Красавицы».
Для каждого работают разные способы объяснения. Мне наиболее понятен такой способ:
Шанс угадать приз, выбрав одну дверь = 1/3. Если выбрать две двери, то шанс становится 2/3. Но в первом туре игроку сделать этого не дают, он вынужден выбрать только одну дверь, получив шанс 1/3. Зато он может сделать это во втором туре, в чем ему помогает ведущий — одну дверь открывает ведущий, игроку остается проверить вторую — момент с «переходом по наследству» совместной вероятности в 2/3 к оставшейся двери основан на том, что ведущий, зная состояние системы, специально открывает именно пустую дверь.
Иллюзия с превращением вероятностей 1/3 + 2/3 в 1/2 + 1/2 перестанет быть иллюзией, если после открывания двери ведущим мы случайным образом переместим приз между двумя дверьми.
perfect_genius
29.10.2016 19:36После такого своему мозгу нет доверия вообще. Сколько всего мы можем не понимать, железно верим в «очевидность». Список когнитивных искажений в Википедии может оказаться далеко не полным.
Errandir
29.10.2016 19:43Предполагаю, что в данных экспериментах люди знали, что они ничего не знают о стратегии, каким образом назначается правильная дверь. И поэтому они особо не парились по поводу выявления этой стратегии: может её нет совсем, а может она поменяется ни с того ни с сего. А для человеческого восприятия вероятности 1/3 и 2/3 достаточно близки к 1/2 при 50-ти испытаниях, тем более без серьёзного стимула.
GebekovAS
01.11.2016 13:52Я все же приверженец такой диаграммы (хоть она и не совсем верная):
Получается, что можно было сменить выбор сразу, не дожидаясь, пока откроют дверь.
Если при выборе 1 к 3 шанс, что мы ошиблись выше, то получается, что есть смысл сразу сменить свой выбор? (другими словами, приблизиться к более вероятной стороне)
Не силен в теории статистики и вероятностей, но почему после открытия двери знаменатель не сменился с 3 на 2? Я так понимаю, в этом случае все задачи теории сводились бы к 50/50?GebekovAS
01.11.2016 14:37+1Хех… до меня таки дошло решение. Ход мыслей:
1. Представил себе ситуацию не 1 / 3, а 1 / 1 000 000.
2. Сделал я выбор и уверен на 99.99%, что он неправильный.
3. Мне открывают остальные 999 998, кроме одной
4. Пришло понятие, почему стоит сменить выбор =)
Я понял, что открытие двери, это уточняющий фактор, которого нет в описанном мною выше примере.
mmatrosov
04.11.2016 16:52Я вот одного не понимаю. Миллионы людей смотрели это шоу десятки лет. Правила всем были известны. Оптимальное решение может найти даже сообразительный школьник. Как такое долгое время люди умудрялись принимать неоптимальное решение? Почему ни одна газета не опубликовала громкую статью с заголовком "Monty Hall Solved!" или типа того?
alibertino
04.11.2016 21:35Это в математике оптимальное решение, а не на шоу. Там нет случайности, равномерного распределения и т.д. Все это работает на больших числах, а в шоу единичные случаи.
mmatrosov
04.11.2016 21:39Хотите сказать, что если бы пошли на шоу, то вы бы могли воспользоваться какой-то другой стратегией?
alibertino
04.11.2016 23:29Я думаю, гораздо больше интересного можно получить от психологии и ведущего, чем от математики в данном случае. Так что да, очевидно, я бы занимался его просчетом, а не дверей. Как, впрочем, и большинство.
Spiritschaser
> на основе Теоремы Байеса об условной вероятности.
Эммм… Я что-то не уловил, где здесь событие-условие?
temujin
Pr(A|B)— вероятность нахождения машины за 1-й дверью, если ведущий показывает 2-ю дверь.ivlis
Пусть C что мне очень захотелось вздремнуть и я забыл загадать какую дверь открывать. Что тогда?
У вас алгебра событий поменялись, потому что точно известно, что за открытой дверью коза, так что ТБ тут не причём.
knstqq
В таком случае вероятность 1/2
ivlis
То есть химическая реакция в моём мозгу превращает козу в машину.
knstqq
нет. Химическая реакция в вашем мозгу стирает дополнительную информацию и вы выбираете уже из двух дверей случайно (а не из трёх).
ivlis
Никакой информации от того что я выбрал не появилось. Она добавилась, когда открыли одну дверь. А у вас получается, что смена одной идентичной двери на другую вдруг уменьшает энтропию системы.
1vanK
Тут можно про вероятность последовательности вспомнить (хотя это не совсем в тему). Монета может выпасть орлом или решкой с вероятностью 50%. И вам говорят вот выпала монета решкой, как она выпадет в следующий раз? Судя по вашей логике она опять выпадет решкой с вероятностью 50%. Получается, что она и третий раз может выпасть с вероятностью 50%. То есть монета может с 50% вероятностью и на сотый раз. То есть у нас помимо вероятности выполнения есть еще информация о прошлых выпадениях. И тут тоже самое. Ведущий может с вероятностью 50% открыть одну из дверей с козами, но 100% не откроет дверь с машиной. И это влияет на вероятность.
ivlis
Хоть после 10^12 падений вероятность выпадения решки 1/2. А вот чтобы 100 раз подряд выпала решка, то это 2^-100 = 7.8*10^-31.
1vanK
Вот например с вами играют в игру. Я кидаю монету и каждый раз вы называете одно и тоже — например решка. Если вы считаете, что вы угадываете каждый раз с 50% вероятностью, то это не так.
ivlis
Если вы не жулик и монета ровная, то это так.
1vanK
Вот нашел таки, я помоему не так пример сформулировал http://books.rusf.ru/unzip/add-on/xussr_mr/melnis11.htm?1/1
ivlis
Что это? Давать текст длиннее чем одна страница без абстракта как-то не принято.
1vanK
Ну сорри, не я автор, претензии не ко мне)
WaterSmith
Вы привели фантастический рассказ, как аргумент в научной дискуссии? Вы серьёзно?
Bimawa
Вы все не правы, так как монета может упасть на ребро, и ваши 50% уже не такие и 50%
Gurklum
Если Вы не против, я немного вмешаюсь в дискуссию с целью внести некоторую ясность.
В опусе по ссылке раскрывается следующий факт: если взять последовательность из выпаданий монетки, то подпоследовательность, например, 100 в ней выпадет раньше, чем подпоследовательность 000.
Скажем, в последовательности 00110100100011, первая подпоследовательность встретилась с 6 позиции (и потом еще с 9), а вторая — с 10й. Этому есть, безусловно, объяснение (схема простая: 000 «выигрывает» только если это и есть старт последовательности, в то время как 100 «выигрывает» и в других ситуациях).
Каким образом это сочетается с постом и комментариями выше, я, однако, объяснять не возьмусь.
RussDragon
https://www.youtube.com/watch?v=SDw2Pu0-H4g
Отличное видео на эту тему.
kryvichh
Хмм, но если 10^12 выпала решка, то в следующий раз вероятность выпадения решки стремится к 100%. Потому что скорее всего монета кривая.
zelenin
речь не про монету, а про идеально рандомный генератор выдающий 0 или 1, если угодно. Не надо подмешивать в условия то, чего в них не было.
Monoroch
Результат выпадения монеты никак не влияет на результаты будущих выпадений.
Ох уж эти «волшебные» объяснения чудесности мартингейла.
mpakep
После того, как монета упала на одно из ребер ведущий знает на какое говорит всегда не верное и предлагает изменить решение. В случае с монеткой вероятность повышается при изменении решения до 100%. Последовательность событий:
Кидаем монетку выпадает решка (к примеру)
Мы не знаем результат и ведущий его знает.
Ведущий говорит что орел не верный результат и предлагает нам изменить свое решение
После чего мы со 100% вероятностью знаем что результат — решка.
Если без изменения нашего решения наши шансы 50% то уже комментарием ведущего наши шансы угадать правильную сторону — 100%
Ohar
Так и есть.
grumegargler
понимаете, тут просто смысл в том, что после того, как открыли дверь, повышается вероятность той двери, которая осталась, и если каждый раз её и выбирать, по вероятности, там чаще окажется машина.
newbie67
Отличный пример есть на вики.
Пусть у нас будет не 3 двери, а 1000. Вы выбрали одну. Ведущий открыл 998 дверей с козлами. Теперь у вас две двери. Теперь очевидно, что за другой дверью шанс намного выше, чем за первоначальной. Т.к. при первоначальном выборе ваши шансы были 1\1000.
В то же время, если вы уснёте и забудете, какую дверь выбрали изначально, то ваши шансы 50\50.
psman
А если не усну? Как процесс прошлых попыток УГАДАТЬ случайное событие влияет на случайность очередного эпизода?
barker
Не процесс прошлых попыток угадать, а прямая подсказка ведущего. Он явно показывает за какой дверью машины нет. Это делает выбор не из равновероятных уже дверей.
Если вы уснёте, то значит забудете какую дверь выбирали изначально вы, а какую выбрал (== не открыл) ведущий (а выбирал он не из ТРЁХ, а из ДВУХ), то есть вы потеряете эту подсказку.
psman
Он может открыть одну дверь с козой
1. когда я угадала
2. когда я не угадал
Если у него нет задачи помочь мне, то он и не помогает. Просто дает шанс с выбора 1/3 перейти к выбору 1/2.
barker
з.ы. Вы поймите, что здесь два состояния у этой дискуссии «вы поняли» и «вы пока не поняли». Вы не можете переспорить и оказаться правым в принципе. Если вы хотите понять — можно ещё пообъяснять, но если вы хотите поспорить с математикой (с ОСНОВАМИ тервера), то увы.
mark_blau
Прямое вмешательство ведущего, внезапно, превращает ваш выбор 1/3 в выбор 1/2, но не 2/3.
Просто это два разных события выбора.
Кроме того, это телевизор, и там выбора нет вовсе.
barker
Durimar123
По моему совсем просто и приближенно к задаче:
Ты выбираешь X дверь из 123.
А затем решаешь, твое будет то, что за выбранной или то что за обеими оставшимися.
какой твой выбор?
дальше объяснять?
psman
Я первый раз выбираю 1 из 3.
Из выбора выкидывают 1 дверь.
Я выбираю 1 из 2.
В ходе всех опытов во время второго выбора постоянно присутствует 1 неверная дверь открытая ведущим. В то время как во время второго выбора мы её просто уже не учитываем.
На том же кругу как раз в данные второго выбор добавляется заведомо неверный ответ (дверь на момент второго выбора открыта)
Durimar123
Все же я не это спросил.
При задаче из 3х дверей выбрать одну, а потом решить открыть её или две оставшиеся.
Ты что выбрал бы?
psman
А в этом примере ведущий откроет одну дверь перед вторым выбором?
Или просто предложит выбрать снова?
Durimar123
Никакого 2го выбора. Сразу все ваше.
Какой ваш выбор? Выбранная или две оставшиеся?
psman
Как нет выбора второго, если я выбрал сначала одну, а уже предлагается выбрать из нее или двух ОСТАВШИХСЯ. Оставшихся после чего?
Durimar123
Хорошо :) ты отметил одну, маркером.
А теперь можешь открыть или ее или две не отмеченные.
И забрать то, что за открытыми дверями себе. :)
psman
Т.е. я опять делаю выбор 1 из 3 и у меня нет подсказки что мой выбор не верен?
Ну кроме сомнения в зависимости от того как у меня в голове «стакан пуст или полон» и я считаю что ведущий пытается мне помешать или помочь
Durimar123
Это другая задача:
Есть 3 двери, за кой-то из них приз.
Одну ты пометил маркером.
Теперь выбери, открыть обе не помеченные или только одну помеченную.
psman
т.е. я выбираю между открытием одной двери или двумя?
Durimar123
Да.
И как ты думаешь какой шанс, для одной двери и для двух?
psman
1/3 и 2/3 по числу открываемых дверей мною.
Durimar123
Допустим ты всегда выбираешь 2двери т.е. шанс 2/3.
Вот скажи, если ты (уже после выбора) попросишь ведущего показать дверь за которой пусто, шанс изменится?
psman
Если я не могу поменять свой выбор, то не меняется, просто он «мучает» меня. И в случае если я выбрал 2 двери обе не верные, то получу просто разочарование полное, а в случай с верным выбором я получаю просто нервы, но радость от выигрыша.
Durimar123
Эмоции оставим в стороне — не тот форрум, тут все сплошь хладнокровные интеллектуалы.
Т.е. видел ты пустую дверь или не видел, шансы не меняются, согласен?
psman
Да, в случае если я не делаю новый выбор, то открытая дверь — это просто констатация факта того что 2 из 3 дверей выбранных мною имеет минимум 1 отрицательный выбор
Durimar123
Конечно — открытие заведомо пустой двери ничего не меняет, шанс остается темже две двери = 2/3, одна = 1/3.
Тогда вопрос, почему ты предположил, что если теперь будет еще один выбор, шансы поменяются?
psman
А с чего в данном случае неверный ответ «прилепляют» к 2/3, говоря про то что я якобы выбрал 2 двери, а не одну?
Durimar123
Это ты про основной сценарий с ведущим?
В первый заход по сути нет выбора, тебе дают пометить любую дверь.
Получаем в помеченной (выбранной) шанс = 1/3.
А в 2х не помеченных шанс = 2/3
пока все верно?
Ratimir
Предвставь, торт разрезают на 3 части и равкладывают на три тарелки. В одну из частей прячут золотое кольцо. И предлягают тебе угадать где оно. Ты берешь одну тарелку в руки. Тут ведущий перекладывает кусок с одной из очтавшихся двух тарелок на другую. И предлагает тебе остаться при своей тарелке или выбрать другую.
Как-то так…
psman
И в этот момент у меня выбор между той что в руке с потенциальным призом и той что осталась с тоже потенциальным призом. Могу выбрать одну из двух.
Ratimir
Да, но вероятность, что кольцо окажется в большем куске, выше.
psman
Если постоянно говорить о том что был первый выбор и нам упростили задачу, то да. Если мы во второй раз делаем выбор между двумя тарелками, то… 1/2. Выбор между той тарелкой что в руке и той что осталась.
Говорить о росте шанса можно только в разрезе сравнения выбора 1 из 3 в первом варианте и удалении из выбора одного объекта.
На том же круге что в статье некорректно показывать дерево выбор именно так. так как во время второго выбора заведомо ложный вариант не участвует в выборе.
psman
Выше чем когда? Сравниваем шансы с первым разом?
edogs
meft
Спасибо, я осознал и понял.
Хотя перед этим читал вики.
По сути у нас 2 двери.
За одной с вероятностью 1/3 будет машина.
За другой — с вероятностью 1/2.
Не нужно на втором этапе думать, что выбор между 2мя дверьми имеет одинаковую вероятность, как у монетки.
Это примерно как следующее.
Кидаем монетку. Монетка может упасть на ребро или одну из двух сторон.
Допустим мы выбрали ребро.
Далее ведущий, который видит будущее, говорит, что монетка в следующий раз точно не упадет на лицевую сторону.
Ну а далее наша ситуация:
или думать, что шанс ребра и оборотной стороны равны, так как осталось всего 2 варианта,
или же думать, что есть оборотная сторона, имеющая шансы 50/50 и есть ребро, которое мы зачем то указали, и шансы которого ничтожно малы.
Ohar
Только после вашего разъяснения я наконец-то понял, в чём дело. Хотя пример с 1000 дверей я тоже понял, но не смог из него сделать правильный вывод.
Спасибо большое.
NINeOneone
Не переживайте, предыдущий комментатор тоже не понял. У него получается, что с вероятностью 1/6 ведущий открыл дверь с машиной, а это не по правилам.
marenkov
У вас утечка
памятишанса.Если есть две двери и у одной шанс быть выигранной 1/3, а у другой 1/2, то с вероятностью 1/6 обе двери проигрышны (т.е. приза нет вообще).
Как только вы выбрали одну дверь, вы разделили шансы на 1/3 и 2/3.
Когда ведущий открывает одну дверь из двух оставшихся ее шанс становиться 0 и все 2/3 достаются оставшейся. Т.е. теперь у вас выбор между выбранной вами 1/3 и оставшимися 2/3.
Bonart
Это неверно. Ведущий не может открыть ту дверь, которую вы выбрали изначально.
barker
Разумеется это не так. Неважно забыли ли вы какую загадывали или нет — вероятность уже изменилась после открытия двери ведущим (читай: его подсказкой).Извиняюсь, не так прочитал. Конечно же если мы видим просто открытую дверь, то не можем знать из каких двух её выбирал для открытия ведущий.barker
facha
Ведущий не просто должен открыть одну из дверей с козлом. Ведущий должин открыть дверь, которую НЕ выбрал конкурсант, и за которой козел. Если Вы уснули и не сделали выбор, ведущий не сможет открыть удовлетворяющую правилам дверь.
perfect_genius
После такого своему мозгу нет доверия вообще. Сколько всего мы можем не понимать, железно верим в «очевидность». Список когнитивных искажений в Википедии может оказаться далеко не полным.