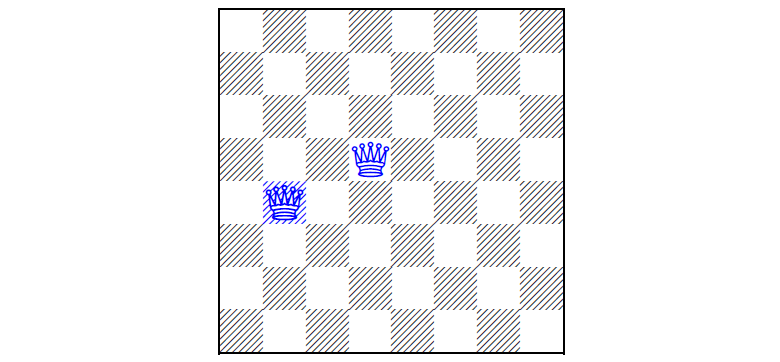
Первый вариант головоломки 1850 года, когда два ферзя заранее установлены на доску, а игрок должен расставить остальных ферзей (два решения задачи см. под катом)
Задача о N ферзях состоит в том, чтобы разместить N ферзей на доске размером N?N таким образом, чтобы ни один ферзь не находился под боем другого, при этом на доске заранее установлены несколько ферзей. То есть в итоге никакие два ферзя не должны находиться на одной линии или диагонали. Впервые задачку сформулировали в 1848 году, а в 1850 году придумали вариант головоломки, когда некоторое количество ферзей заранее поставлено на доску, а игрок должен расставить остальных, если это возможно.
Исследователи из Сент-Эндрюсского университета (Шотландия) опубликовали научную статью, в которой доказывают, что задача о N ферзях является не только #P-полной задачей, но также NP-полной задачей. Более того, Математический институт Клэя (США) готов заплатить миллион долларов любому, кто сможет оптимизировать решение этой задачи как задачи на доказательство P=NP.
Как известно, в теории сложности #P является классом проблем, решением которых является количество успешных, то есть, завершающихся в допускающих состояниях, путей вычислений для некой недетерминированной машины Тьюринга, работающей полиномиальное время. Вычислительные задачи класса #P (counting problems) связаны с соответствующими задачами разрешимости (decision problems) класса NP.
Учёные отмечают, что эта задача может быть самой простой среди NP-полных задач, чтобы объяснить суть этих проблем любому человеку, который знает правила игры в шахматы. У этой задачи вообще очень интересная история. В своё время она привлекла внимание Гаусса, который даже сделал небольшую ошибку в её решении (на доске 8?8 он сообщил о 76 решениях, но потом сам признал четыре из них ошибочными, так что остались только 72, а позже Гаусс установил все 92 решения для доски 8?8).
Обобщение задачи для доски N?N привлекло внимание многих математиков. За последние полвека вышло несколько десятков научных работ, посвящённых этой проблеме. Как минимум шесть из них цитируются более 400 раз на Google Scholar: это Golomb & Baumert, 1965; Bitner & Reingold, 1975; Mackworth & Freuder, 1985; Minton, Johnston, Philips, & Laird, 1992; Selman, Levesque & Mitchell, 1992; Crawford, Ginsberg, Luks, & Roy, 1996.
Сложность задачи о N ферзях часто неправильно оценивают. Даже в обильно цитируемых работах её часто называют NP-сложной задачей (NP-hard), но она будет таковой только при условии, что P=NP. На самом деле вычислительный вариант задачи, то есть определение количества решений для N ферзей, представляет собой последовательность A000170 из Онлайн-энциклопедии целочисленных последовательностей. Эта последовательность сейчас известна максимум для n=27, где количество решений превышает 2,34?1017. Не известно ни одно более эффективное решение проблемы, чем простой перебор. Так, для n=27 в 2016 году использовался масштабный параллельный поиск на FPGA.
В то же время, если компьютер начнёт перебор возможных положений ферзей на доске 1000?1000 клеток, то он загрузится этой задачей навечно. По мнению учёных, если некто найдёт действительно быстрый и эффективный способ решения, то сможет извлечь из этого гораздо бoльшую выгоду, чем один миллион долларов от Математического института Клэя. «Если вы напишете программу, которая может решить проблему действительно быстро, вы могли бы адаптировать её для решения многих важных задач, с которыми мы сталкиваемся ежедневно, — говорит профессор информатики Ян Гент (Ian Gent), один из авторов научной работы. — Среди них тривиальные проблемы, такие как поиск самой большой группы ваших друзей в Facebook, которые не знают друг друга, или очень важные задачи, например, взлом кодов, которые обеспечивают безопасность всех наших онлайн-транзакций».
Но это чисто теоретические измышления. На практике никто пока не приблизился к решению задачи о N ферзях быстрым и эффективным способом. За доказательство, что существует более эффективный способ решения задачи, чем простой перебор всех вариантов, дадут миллион долларов.
Научная статья опубликована в августе 2017 года в журнале Journal of Artificial Intelligence Research (doi:10.1613/jair.5512, pdf).
P.S. Два решения задачи с КДПВ:

Комментарии (45)

ripatti
03.09.2017 22:03+1Класс #P принадлежит к классу NP...
Тут какой-то бред написан. Мало того, что любая задача из #P не проще аналогичной из NP, они еще и в разных «весовых категориях» — у задачи из #P на выходе число (counting problem), а у задачи из NP — «да» или «нет» (decision problem), и для «да» есть сертификат, проверяемый за полином. И вот мы для задачи из #P получили число — и как мы проверим за полином, что это число верное, раз эта задача еще и в NP лежит?
alizar Автор
03.09.2017 23:13Я исправил формулировку, действительно, было не совсем корректно. Спасибо, что обратили внимание!

CDCrom
03.09.2017 22:17В головоломке говорится о том, что нужно на доске 8 на 8 расположить 8 ферзей, а то у меня для указанного варианта получилось 7 ферзей покрывающих все поле.

CDCrom
03.09.2017 22:18+2Простите, я не правильно прочел статью… перечитал, понял, что нельзя писать на ночь глядя… а отменить отправку уже не смог:(

LoadRunner
03.09.2017 23:26О, так вот как называется задача о 9 мухах. И судоку, в принципе, тоже из этого же класса задач.
А в представленных в статье 2 решениях две группы по 3 ферзя просто переставлены. Что приводит к мысли, что для нахождения всех решений надо найти одно верное, а все остальные получаются из всех возможных перестановок.
qw1
04.09.2017 00:42+1Для доски 4x4 есть всего 2 решения (причём одно получается из другого зеркальным отражением или поворотом). Что тут можно попереставлять?
-X--
---X
X---
--X-

LoadRunner
04.09.2017 08:42Зеркальное отражение — это просто название одной из перестановок.
В случае N=4, других просто нет. Ну и 4 — минимальное число для данной задачи.
Не спорю, зеркальные отражения и повороты не порождают новых вариантов, а являются эквивалентом уже существующих. Но эти эквиваленты легко получаются перестановками.
darkdaskin
04.09.2017 09:35+24 — минимальное число для данной задачи
Формально есть ещё одно решение для доски 1?1.

qw1
04.09.2017 12:25Тогда, в принципе, любую расстановку можно назвать перестановкой другой расстановки.
Вы хотели подчеркнуть какое-то более интересное свойство? Не просто перестановку, а перестановку группы?

varagian
04.09.2017 01:03+5Заголовок не верен, да ещё и пост не проясняет суть статьи *злой и расстроенный смайл одновременно*.
Задача в варианте:
- найти решение в виде N ферзей на доске N*N — в P (вообще там чуть ли не линейное время);
- найти число решений для доски N*N — не имеет решения в закрытой форме (вне #P);
- дополнение доски N*N до N ферзей, уже имея M (<N) — NP-complete и #P-complete (в этом результат статьи!).
(Если что, это всё написано в самой статье в разделе Introduction.)

Sayonji
04.09.2017 13:11NP-полным будет только вопрос о том, сколько решений? Или есть ли хотя бы одно решение уже тоже NP-полная задача?

varagian
04.09.2017 13:17+1Сколько решений вообще выше, чем #P и NP — то есть у нас вообще нет никакой аналитической формулы для решения.
Если доска пустая, то одно решение находится за линейное время (кажется линейное, но точно в P, то есть полином — корочь, точно не NP-полна задача).
Если доска не пустая и на ней уже стоит M ферзей и всего нужно N, т.е. нужно ещё N — M доставить до N, то задача NP-полна, как следует из только что опубликованной статьи.erwins22
04.09.2017 15:08Тогда за что 1млн баксов????

qw1
04.09.2017 15:57+1За решение задачи дополнения.
Т.е. на доске NxN стоит M ферзей (M < N).
Нужно доставить N-M, чтобы получилось N, либо определить, что в данной конфигурации это невозможно. И сделать это за P-время.erwins22
04.09.2017 16:20Надо найти число таких комбинаций, все такие комбинации или просто факт, если или нет?
У этих задач разная оценка сложности.
qw1
04.09.2017 17:05+1Надо найти одну комбинацию или доказать, что такой нет.
erwins22
04.09.2017 17:12Спасибо.
Доказать что есть без предъявления конкретной пройдет?
varagian
04.09.2017 17:59Не, если ответ «да», то нужно вернуть сертификат проверяемый за полиномиальное время.
В данном случае, N ферзей (ну или N-M сути в общем-то не играет).

qw1
04.09.2017 23:24Доказать что есть без предъявления конкретной пройдет?
А сможете формализовать?
Решение SAT-задачи — вектор значений переменных.
Решение задачи расстановки — координаты ферзей.
Сможете придумать «доказательство» в виде числового вектора, правильность которого (т.е. то, что он есть доказательство, а не рандомный набор) можно проверить за P-время?
Если сможете, то пройдёт. Т.е. нужно научиться генерировать такие вектора за P-время и уметь их проверять за P-время.erwins22
04.09.2017 23:41аналогия — проверка простоты числа без указания конкретного делителя.

qw1
05.09.2017 15:09Непонятная аналогия. Я знаю, есть правила деления на 3, 5 и т.д.
Т.е. в частных случаях мы можем быстро сказать «Нет, не не простое». Но не можем быстро сказать «да» или «нет» во всех случаях.

Sayonji
05.09.2017 12:38+1Пройдет, «сертификат» это всё шелуха. Если ваша программа будет правильно отвечать ДА/НЕТ на данную задачу за полиномиальное время, то, используя её как функцию, можно будет на все NP задачи правильно отвечать ДА/НЕТ, это определение NP-сложной задачи.
Альтернативный ответ на ваш вопрос: если у вас есть алгоритм, правильно отвечающий ДА/НЕТ, то можно, получив ответ ДА, доставлять одного ферзя всеми способами и искать такого, что ответ вашего алгоритма будет снова ДА. Как только найдем, пытаться ставить следующего. И так далее, мы за N^3 попыток поставим всех ферзей, т. е. на полином запусков вашего алгоритма найдем «сертификат».

cujos
04.09.2017 07:15За доказательство, что существует более эффективный способ решения задачи, чем простой перебор всех вариантов, дадут миллион долларов.
Как-то не однозначно звучит. Кому в голову придет перебирать «все» варианты? Потому как добавление каждого ферзя убирает 3.х*n заведомо неверных вариантов расстановки нового ферзя. Запилить рекурсию и перебирать из оставшихся не так сложно. Или они хотят алгоритм расстановки каждого следующего ферзя в заведомо правильное место?menfromearth
04.09.2017 11:37Да тут вся статья признана запутать читателя, похоже. Одна фраза «не только #P-полной задачей, но также NP-полной» чего стоит. Естественно, формально, требуется найти полиномиальный по времени алгоритм. Лучше прочитайте исходную статью — там и само доказательство несложное (особенно, ели сравнить с аналогичными результатами в выч геоме).

Konachan700
04.09.2017 11:49У меня получилось за 10 минут и без рекурсии решить на С. Перебором, ясно дело — 31 проход по доске 40х40. С уже предустановленной в случайном месте фигурой. Наверняка знакомый с математикой человек сделает код еще оптимальнее.
В задаче же, насколько я понял, хотят иметь формулу, от которой из позиции одной фигуры можно посчитать позицию следующей. На большой доске, кстати говоря, во всех случаях расстановки видно некий паттерн (ход коня) для групп фигур, который наверняка что-то значит…
LoadRunner
04.09.2017 13:16+1Да, он значит, что нет пересечений по строке, столбцу и диагонали. Это минимальное расстояние между двумя клетками, которые удовлетворяют данному правилу.

Konachan700
04.09.2017 19:10Это я понял уже. Забавная задачка. Кажется очень легкой, но на деле нет. Поигрался, даже формулу вывел, которой можно заполнять без перебора всё поле:
Заголовок спойлераmisaki@linux-nh28:~/devel/test.2> ./test X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | Time: 0.00 Count: 19
mobi
04.09.2017 22:46А для четного N?

Konachan700
05.09.2017 10:18Для разных случаев по-разному считается. Разбирался бы я в математике, можно было бы совсем общую формулу вывести, принцип вроде во всех случаях один.
Вот поле 22х22.misaki@linux-nh28:~/devel/test.2> ./test X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | | | | | | | | X | | | | Time: 0.00 Count: 20
mobi
05.09.2017 10:49А тут число ферзей (20) не равно размеру доски (22).

Konachan700
05.09.2017 13:14Да, не всегда равно. Но просматривается какая-то зависимость. В алгоритме после формулы еще работает перебор — если бы были еще возможные позиции, их сразу стало бы видно.

LoadRunner
05.09.2017 17:28У вас пропущено в центре две строки, из-за этого вся теория рушится. Для нечётного — всё отлично, а вот для чётного всегда будет пересечение по диагоналям при такой схеме заполнения.

Konachan700
05.09.2017 17:39Да, что-то не то. Чуток поправил, теперь все ок:
Board size: 15 x 15> ./test Time: 6 ns X | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | X | | | | | | | | | | | | | | | | X | | | Count: 14 Board size: 15 x 15
LoadRunner
05.09.2017 18:52А сейчас даже на нечётной пропущена строка (как и на чётной).
Не зря эта задача сложная.
Konachan700
05.09.2017 21:16Так почему пропуск строки важен? Вики вроде ничего об этом не говорит. Вот код которым я проверял — от 21 до 1000 крутил — везде нет пересечений, и везде максимально плотное заполнение. Там магия правда местами…

LoadRunner
06.09.2017 08:16Потому что надо N ферзей разместить на доске NxN. А у Вас N-1 ферзь получается.

Anthrax_Beta
04.09.2017 14:13+2На самом же деле, задача была впервые поставлена в 1848 г. немецким шахматистом М. Беццелем. Гаусс же нашел 72 решения, которые и сообщил в письме к другу астроному Шумахеру в сентябре 1850 года. Полный набор решений состоит из 92 позиций. Существенных решений (не совпадающих при отражениях и поворотах доски) имеется только двенадцать. Остальные 80 расстановок получаются из этих двенадцати при помощи поворотов и отражений доски.


qw1
Интересно, они свели 1-in-3-SAT (т.е. NP-полную задачу) к задаче расстановки ферзей.
Научимся расставлять ферзей — научимся решать SAT