Продолжаем цикл статей по работе с API САПР КОМПАС-3D Сергея Норсеева, инженера-программиста АО «ВНИИ «Сигнал», автора книги «Разработка приложений под КОМПАС в Delphi». В качестве среды используется C++ Builder. В предыдущих уроках по API КОМПАС Основы и Оформление чертежа мы исходили из того, что КОМПАС не запущен, в уроке Корректное подключение к КОМПАС мы проверяли наличие уже запущенного КОМПАСа и подключались к нему. В уроке Основная надпись разбирали, как заполнить основную надпись чертежа. В прошлом уроке Графические примитивы мы начали чертить первые геометрические фигуры. В данной статье рассматриваются различные способы построения дуги окружности. В КОМПАС ее можно построить тремя различными способами. Мы рассмотрим их все.

Вначале определимся с тем, что будем строить. Для примера предлагаю взять полуокружность радиуса 10 мм с центром в точке с координатами (100, 100). Данная дуга показана на рисунке ниже.
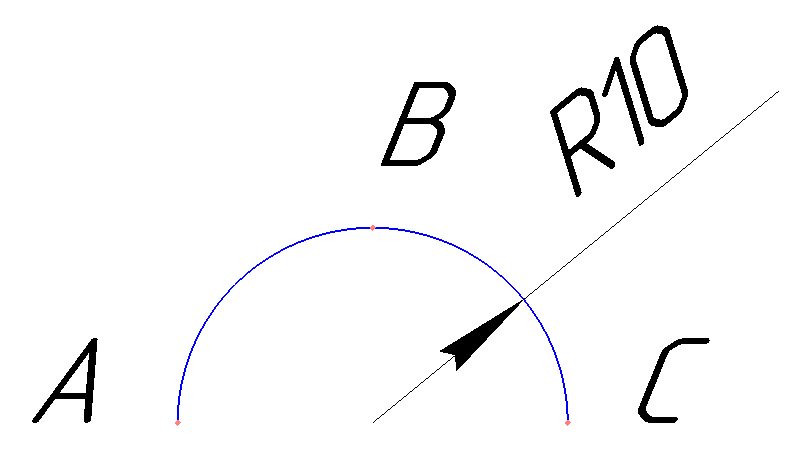
(Картинка кликабельна).
A, B и C – вспомогательные точки, которые пригодятся нам при описании различных способов построения дуги.
Первый способ основывается на том, что вам известны координаты точек A, B и C, но неизвестны координаты центра. Для построения дуги по трем точкам используется метод ksArcBy3Points интерфейса ksDocument2D. Ниже приводится его прототип.
Стили линии обсуждались в предыдущей статье цикла.
В случае успеха метод возвращает указатель на построенную дугу, а в случае ошибки – значение ноль.
Для построения нашей дуги нужно определиться с координатами точек. Так, точка A имеет координаты (90, 100), точка B (100, 110), точка C (110, 100). При таких исходных данных вызов метода ksArcBy3Points должен производиться так, как показано ниже.
О том, как получить указатель на интерфейс ksDocument2D, рассказывалось в предыдущих статьях цикла.
Данный способ основан на том, что вам известны координаты центра дуги и углы ее концов. Для построения дуги по этой информации используется метод ksArcByAngle интерфейса ksDocument2D. Ниже приводится прототип этого метода.
С параметрами xc, yc, rad и style, думаю, всё ясно. С ними вопросов возникнуть не должно.
Параметры f1 и f2 задают углы (в градусах) между прямыми, проходящими через центр дуги и ее конечные точки, и горизонтальной прямой. Данные углы показаны на рисунке ниже.
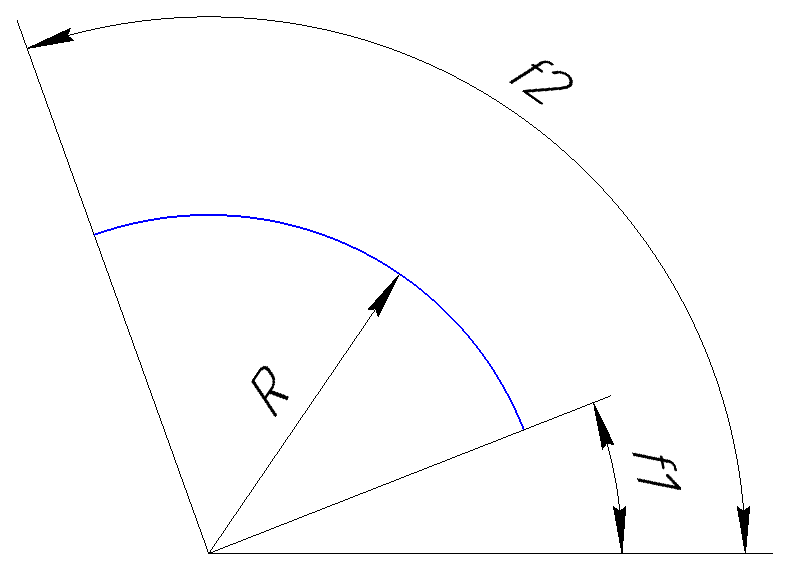
Теперь по поводу параметра direction. Он задает направление, в котором следует отрисовывать дугу. Если он равен 1, то дуга строится против часовой стрелки, если же он равен -1, то дуга строится по часовой стрелке. Например, дуга, изображенная на рисунке выше, отрисована против часовой стрелки, а на рисунке ниже представлена дуга, построенная с теми же параметрами, но по часовой стрелке.
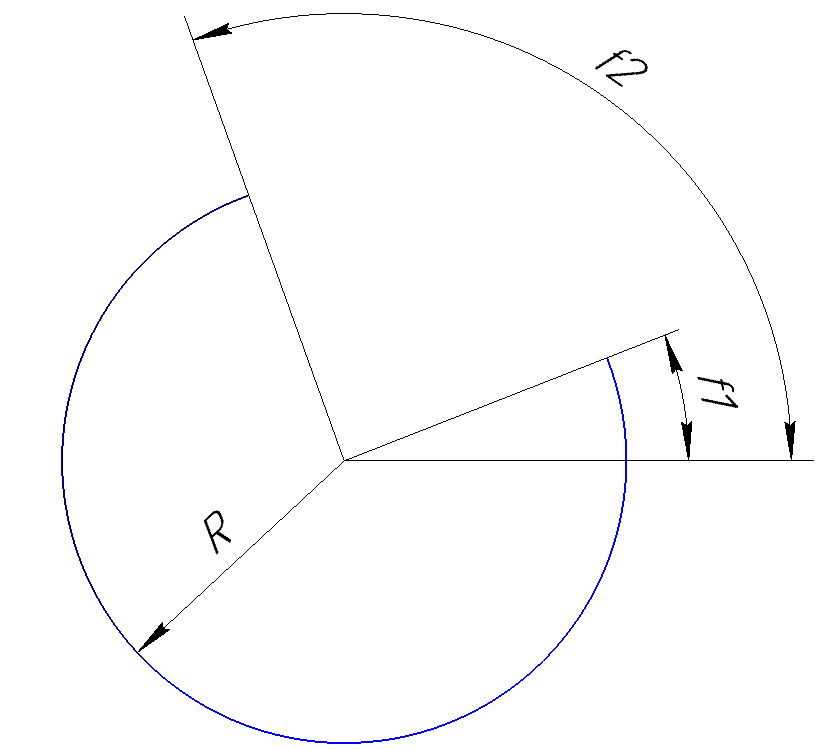
В случае успеха метод ksArcByAngle возвращает указатель на построенную дугу, а в случае ошибки — значение ноль.
Вернемся к нашей задаче построения дуги. Для ее отрисовки против часовой стрелки углы должны быть заданы следующим образом: f1 = 0, f2 = 180. Для отрисовки этой же дуги по часовой стрелке значения углов нужно поменять местами (f1 = 180, f2 = 0).
Код построения дуги приведен ниже.
Данный способ основан на том, что вам известны координаты центра дуги и координаты конечных точек дуги. Для построения дуги по этой информации используется метод ksArcByPoint интерфейса ksDocument2D. Ниже приводится прототип этого метода.
Данный метод очень похож на рассмотренный ранее метод ksArcByAngle. Разница состоит лишь в том, что конечные точки задаются не углами, а координатами.
В случае успеха метод ksArcByPoint возвращает указатель на дугу, а в случае ошибки — ноль.
Ниже приводится код вызова этого метода для построения нашей дуги.
Внимательный читатель наверняка заметил, что параметры метода ksArcByPoint являются избыточными. Почему? Неужели ошибка создателей API? На самом деле нет. Просто нужно правильно понимать назначение точек (x1, y1) и (x2, y2). Согласно документации КОМПАС:
x1, y1 – координаты начальной точки дуги,
x2, y2 – координаты конечной точки дуги.
Такое неправильное описание и создает путаницу. На самом деле точки (x1, y1) и (x2, y2) могут не принадлежать дуге. Они задают не положение конечных точек, а ориентацию вектора, на котором они находятся. Причем начало этого вектора находится в центре дуги. Рисунок ниже поясняет это более наглядно.
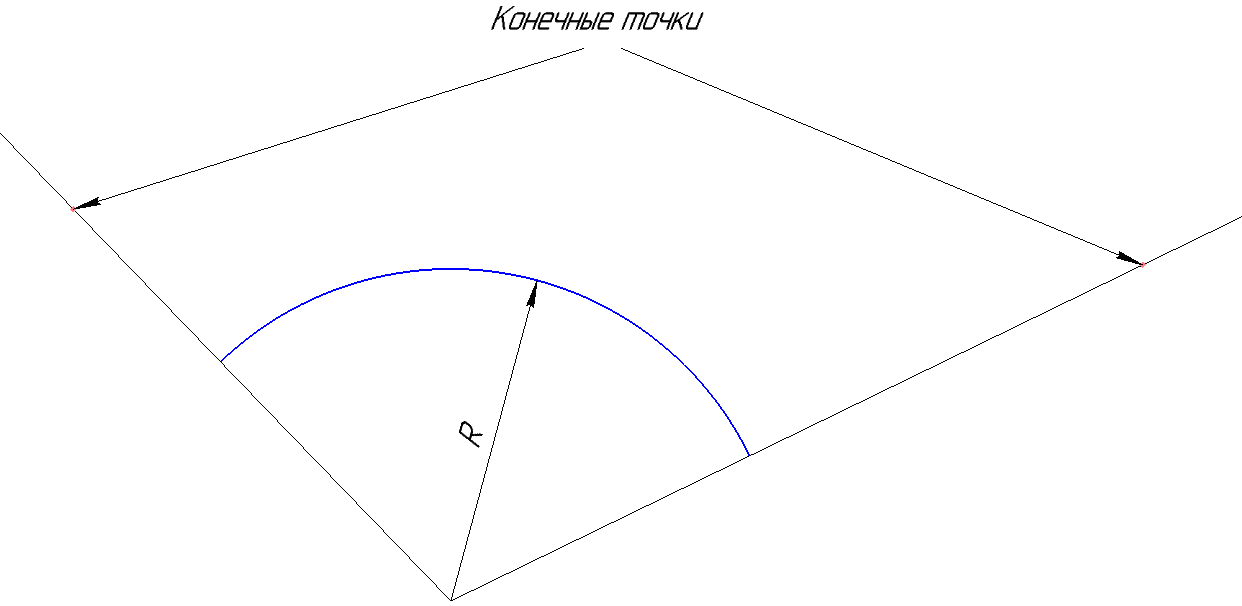
Исходя из этого, рассматриваемую нами дугу можно построить с помощью кода, приведенного ниже.
Обратите внимание: конечные точки не совпадают с точками A и C, но дуга все равно строится правильно.
Заключение
В данной статье мы рассмотрели различные способы построения дуги окружности. Каким из них пользоваться, решайте сами. Но я думаю, что ваше решение будет определяться той информацией о дуге, которая у вас есть в данный момент времени.
Продолжение следует, следите за новостями блога.
 Сергей Норсеев, автор книги «Разработка приложений под КОМПАС в Delphi».
Сергей Норсеев, автор книги «Разработка приложений под КОМПАС в Delphi».

Постановка задачи
Вначале определимся с тем, что будем строить. Для примера предлагаю взять полуокружность радиуса 10 мм с центром в точке с координатами (100, 100). Данная дуга показана на рисунке ниже.

(Картинка кликабельна).
A, B и C – вспомогательные точки, которые пригодятся нам при описании различных способов построения дуги.
По трем точкам
Первый способ основывается на том, что вам известны координаты точек A, B и C, но неизвестны координаты центра. Для построения дуги по трем точкам используется метод ksArcBy3Points интерфейса ksDocument2D. Ниже приводится его прототип.
long ksArcBy3Points ( double x1, //Координаты первой точки
double y1,
double x2, //Координаты второй точки
double y2,
double x3, //Координаты третьей точки
double y3,
long style);//Стиль линии
Стили линии обсуждались в предыдущей статье цикла.
В случае успеха метод возвращает указатель на построенную дугу, а в случае ошибки – значение ноль.
Для построения нашей дуги нужно определиться с координатами точек. Так, точка A имеет координаты (90, 100), точка B (100, 110), точка C (110, 100). При таких исходных данных вызов метода ksArcBy3Points должен производиться так, как показано ниже.
Document2D->ksArcBy3Points( 90 , 100, //Точка А
100, 110, //Точка B
110, 100, //Точка C
1); //Cтиль линии
О том, как получить указатель на интерфейс ksDocument2D, рассказывалось в предыдущих статьях цикла.
По центру и углам
Данный способ основан на том, что вам известны координаты центра дуги и углы ее концов. Для построения дуги по этой информации используется метод ksArcByAngle интерфейса ksDocument2D. Ниже приводится прототип этого метода.
long ksArcByAngle ( double xc, //Координаты центра
double yc,
double rad, //Радиус
double f1, //Углы
double f2,
short direction, //Направление отрисовки
long style); //Стиль линии
С параметрами xc, yc, rad и style, думаю, всё ясно. С ними вопросов возникнуть не должно.
Параметры f1 и f2 задают углы (в градусах) между прямыми, проходящими через центр дуги и ее конечные точки, и горизонтальной прямой. Данные углы показаны на рисунке ниже.

Теперь по поводу параметра direction. Он задает направление, в котором следует отрисовывать дугу. Если он равен 1, то дуга строится против часовой стрелки, если же он равен -1, то дуга строится по часовой стрелке. Например, дуга, изображенная на рисунке выше, отрисована против часовой стрелки, а на рисунке ниже представлена дуга, построенная с теми же параметрами, но по часовой стрелке.

В случае успеха метод ksArcByAngle возвращает указатель на построенную дугу, а в случае ошибки — значение ноль.
Вернемся к нашей задаче построения дуги. Для ее отрисовки против часовой стрелки углы должны быть заданы следующим образом: f1 = 0, f2 = 180. Для отрисовки этой же дуги по часовой стрелке значения углов нужно поменять местами (f1 = 180, f2 = 0).
Код построения дуги приведен ниже.
Document2D->ksArcByAngle( 100, 100, //Координаты центра
10, //Радиус
0, 180, //Углы
1, //Против часовой стрелки
1); //Cтиль линии
По центру и конечным точкам
Данный способ основан на том, что вам известны координаты центра дуги и координаты конечных точек дуги. Для построения дуги по этой информации используется метод ksArcByPoint интерфейса ksDocument2D. Ниже приводится прототип этого метода.
long ksArcByPoint ( double xc, //Координаты центра
double yc,
double rad, //Радиус
double x1, //Координаты первой конечной точки
double y1,
double x2, //Координаты второй конечной точки
double y2,
short direction, //Направление
long style); //Стиль линии
Данный метод очень похож на рассмотренный ранее метод ksArcByAngle. Разница состоит лишь в том, что конечные точки задаются не углами, а координатами.
В случае успеха метод ksArcByPoint возвращает указатель на дугу, а в случае ошибки — ноль.
Ниже приводится код вызова этого метода для построения нашей дуги.
Document2D->ksArcByPoint( 100, 100, //Координаты центра
10, //Радиус
110, 100, //Точка C
90 , 100, //Точка A
1, //Против часовой стрелки
1); //Стиль линии
Внимательный читатель наверняка заметил, что параметры метода ksArcByPoint являются избыточными. Почему? Неужели ошибка создателей API? На самом деле нет. Просто нужно правильно понимать назначение точек (x1, y1) и (x2, y2). Согласно документации КОМПАС:
x1, y1 – координаты начальной точки дуги,
x2, y2 – координаты конечной точки дуги.
Такое неправильное описание и создает путаницу. На самом деле точки (x1, y1) и (x2, y2) могут не принадлежать дуге. Они задают не положение конечных точек, а ориентацию вектора, на котором они находятся. Причем начало этого вектора находится в центре дуги. Рисунок ниже поясняет это более наглядно.

Исходя из этого, рассматриваемую нами дугу можно построить с помощью кода, приведенного ниже.
double xc = 100;
double yc = 100;
Document2D->ksArcByPoint( xc, yc, //Координаты центра
10, //Радиус
xc+1, yc, //Первая конечная точка
xc-1, yc, //Вторая конечная тока
1, //Против часовой стрелки
1); //Стиль линии
Обратите внимание: конечные точки не совпадают с точками A и C, но дуга все равно строится правильно.
Заключение
В данной статье мы рассмотрели различные способы построения дуги окружности. Каким из них пользоваться, решайте сами. Но я думаю, что ваше решение будет определяться той информацией о дуге, которая у вас есть в данный момент времени.
Продолжение следует, следите за новостями блога.
 Сергей Норсеев, автор книги «Разработка приложений под КОМПАС в Delphi».
Сергей Норсеев, автор книги «Разработка приложений под КОМПАС в Delphi». 
