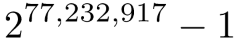
Роли, Северная Каролина, 3 января 2018 года — организация Great Internet Mersenne Prime Search (GIMPS, масштабный Интернет-проект по поиску простых чисел Мерсенна) обнаружила самое большое известное простое число 2^77232917-1, состоящее из 23 249 425 разрядов. Компьютер волонтёра Джонатана Пейса вычислил его 26 декабря 2017 года. Джонатан — один из тысяч добровольцев, использующих бесплатное ПО GIMPS.

Новое простое число, также известное как M77232917, вычислено перемножением 77 232 917 двоек и вычитанием единицы. Оно примерно на один миллион разрядов больше, чем предыдущее рекордное простое число, в особом классе исключительно редких простых, известных как числа Мерсенна. Это всего пятидесятое открытое простое число Мерсенна; вычисление каждого последующего становится сложнее. Простые числа Мерсенна названы по имени французского монаха Марина Мерсенна, изучавшего эти числа больше 350 лет назад. Основанная в 1996 году GIMPS обнаружила последние 16 простых чисел Мерсенна. Волонтёры скачивают бесплатную программу для поиска этих простых чисел и имеют шанс выиграть денежный приз, если им повезёт найти новое число.
У профессора Криса Колдуэлла есть авторитетный веб-сайт, посвящённый самым большим известным простым числам с замечательной историей простых чисел Мерсенна.

Проверка простоты заняла шесть дней безостановочных вычислений на PC с процессором Intel i5-6600. Чтобы доказать, что в процессе обнаружения простых чисел нет ошибок, новое простое число проверяется в четырёх разных программах на четырёх различных конфигурациях оборудования.

• Аарон Блоссер проверил его с помощью Prime95 на сервере Intel Xeon за 37 часов.
• Дэвид Стэнфилл проверил число в gpuOwL на видеопроцессоре AMD RX Vega 64 за 34 часа.
• Андреас Хоглунд проверил простое число с помощью CUDALucas на видеопроцессоре NVidia Titan Black GPU за 73 часа.
• Эрнст Майер проверил число в собственной программе Mlucas на 32-ядерном сервере Xeon за 82 часа. Андреас Хоглунд подтвердил его результаты, прогоняя Mlucas на виртуальной машине Amazon AWS 65 часов.

Джонатан Пейс — 51-летний инженер-электромеханик, живущий в Джермантауне, штат Теннесси. Его упорство наконец было вознаграждено — Джонатан охотился за большими простыми числами с GIMPS более 14 лет. За своё открытие он получил от GIMPS исследовательскую награду в 3 000 долларов.

Клиентское ПО Prime95 разработано основателем GIMPS Джорджем Уолтманом. Скотт Куровски написал системное ПО PrimeNet, координирующее компьютеры GIMPS. Аарон Блоссер теперь работает системным администратором и при необходимости выполняет обновление и обслуживание PrimeNet. Волонтёры имеют шанс получить вознаграждение в 3 000 или 50 000 долларов, если их компьютер откроет новое простое число Мерсенна. Следующей крупной целью GIMPS является выигрыш учреждённой Electronic Frontier Foundation награды в 150 000 долларов, которая будет вручена за нахождение простого числа со 100 000 000 разрядов.

Мы признательны за нахождение этого простого числа не только Джонатану Пейсу, выполнявшему на своём компьютере ПО Prime95: Уолтману за написанное ПО, Куровски и Блоссеру за их работу с сервером Primenet, а также тысячам добровольцев GIMPS, просеявшим миллионы вариантов чисел. В благодарность всем этим людям официально это открытие приписывается «Дж. Пейсу, Дж. Уолтману, С. Куровски, А. Блоссеру и коллегам».

Про Great Internet Mersenne Prime Search

Организация Great Internet Mersenne Prime Search (GIMPS) была сформирована в январе 1996 года Джорджем Уолтмана для нахождения новых мировых рекордов простых чисел Мерсенна. В 1997 году Скотт Куровски обеспечил GIMPS возможность использовать мощь тысяч обычных компьютеров для поиска этих «иголок в стоге сена». Большинство участников GIMPS вступило в организацию ради захватывающей возможности обнаружения рекордного, редкого и исторического нового простого числа Мерсенна. Поиск следующих простых чисел Мерсенна уже продолжается. Возможно, существуют и меньше, но пока ненайденные простые, и почти абсолютно точно есть бОльшие, ждущие своего обнаружения. Любой человек с достаточно мощным компьютером может присоединиться к GIMPS и стать охотником за большими простыми числами с возможностью получить денежную награду за своё открытие. Всё необходимое ПО можно бесплатно скачать по адресу www.mersenne.org/download/. GIMPS сформирована как Mersenne Research, Inc., некоммерческая научная благотворительная организация 501(с)(3). Подробнее об этом можно прочитать на www.mersenneforum.org и www.mersenne.org; также принимаются добровольные пожертвования.

Дополнительная информация о простых числах Мерсенна

Простые числа давно восхищали и любителей, и профессионалов математики. Целое число больше единицы называется простым числом, если его единственными делителями являются единица и оно само. Первые простые числа: 2, 3, 5, 7, 11 и т.д. Например, число 10 не является простым, потому что делится на 2 и 5. Простое число Мерсенна — это простое число, имеющее вид 2^P — 1. Первыми простыми числами Мерсенна являются 3, 7, 31 и 127, соответствующие P = 2, 3, 5 и 7. Пока известно 50 простых чисел Мерсенна.

Простые числа Мерсенна были в центре внимания теории чисел с тех пор, когда их впервые рассмотрел Евклид около 350 до нашей эры. Человек, именем которого назвали эти числа, французский монах Марин Мерсенн (1588-1648 гг.), создал знаменитую гипотезу о том, при каких значениях P можно получить простое число. Чтобы подтвердить эту гипотезу, потребовались 300 лет и несколько важных открытий.

Сегодня есть мало практических применений этого простого числа, что заставляет некоторых задаваться вопросом: «Зачем вообще искать такие большие простые числа»? Подобные сомнения существовали и несколько десятилетий назад, пока наконец не были разработаны важные криптографические алгоритмы на основе простых чисел. Ещё семь хороших причин для поиска больших простых чисел изложены здесь.

Предыдущие открытия простых чисел Мерсенна в рамках GIMPS были совершены участниками из разных стран.


Евклид доказал, что каждое простое число Мерсенна генерирует совершенное число. Совершенное число — это число, сумма собственных делителей которого равно самому числу. Самым малым совершенным числом является 6 = 1 + 2 + 3, вторым — 28 = 1 + 2 + 4 + 7 + 14. Эйлер (1707-1783 гг.) доказал, что все чётные совершенные числа являются результатом простых чисел Мерсенна. Последнее открытое совершенное число — это 2^77232916 x (2^77232917-1). Это число имеет более 46 миллионов разрядов! Всё ещё неизвестно, существуют ли нечётные совершенные числа.

Арифметические алгоритмы, лежащие в основе проекта GIMPS, имеют уникальную историю. Программы, нашедшие последние большие простые числа Мерсенна, основаны на специальном алгоритме. В начале 1990-х ныне покойный Ричард Крэндэлл, выдающийся учёный из Apple, обнаружил способы удвоения скорости выполнения свёрток — очень больших операций умножения. Этот метод применим не только ко поиску простых чисел, но и к другим аспектам вычислений. В процессе работы над этим проектом он также запатентовал систему шифрования Fast Elliptic Encryption, которая теперь принадлежит Apple Computer. В ней для быстрой шифровки и дешифровки сообщений используются простые числа Мерсенна. Джордж Уолтман реализовал алгоритм Крэндэлла на языке ассемблера, создав таким образом программу поиска простых чисел с беспрецедентной эффективностью. Эта работа привела к созданию успешного проекта GIMPS.

Школьные учителя используют GIMPS, чтобы заинтересовать своих учеников математикой. Студенты, запустившие на своих компьютерах ПО, вносят свой вклад в математические исследования.

---

Дополнение из поста Джона Д. Кука.


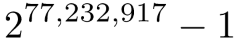
Это число содержит состоит из 23 249 425 разрядов при записи в десятичном виде.

В двоичном виде 2^p – 1 является последовательностью из p единиц. Например, 31 = 2⁵ — 1 равно в двоичном виде 11111. То есть в двоичном виде новое рекордное простое число является строкой из 77 232 917 единиц.


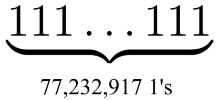
Двоичное число можно преобразовать в шестнадцатеричное (основание 16), начав с правого конца и преобразуя блоки из четырёх бит в шестнадцатеричные числа. Например, для преобразования 101101111 в HEX, мы разобьём число на три блока: 1, 0110 и 1111. Эти блоки преобразуются в 1, 6 и F, то есть двоичное 101101111 соответствует шестнадцатеричному 16F.

Далее, 77 232 917 = 19 308 229 * 4 + 1, то есть мы разбиваем нашу строку из 77 232 917 единиц в группы из четырёх цифр, получив один оставшийся бит, за которым следуют 19 308 229 групп из четырёх цифр. Это значит, что в шестнадцатеричной записи новое рекордное простое число имеет вид 1FFF…FFF — единица, за которой следуют 19 308 229 F.


Новый рекорд — это 50-е простое число Мерсенна. Простое число Мерсенна — это простое число на единицу меньше степени двойки, т.е. имеет вид 2^p – 1. Оказалось, что для простоты 2^p – 1 число p тоже должно быть простым. В случае нового рекорда 77 232 917 является простым.

Неизвестно, существует ли бесконечное количество простых чисел Мерсенна. Но теперь мы знаем, что их как минимум 50.

Все последние рекорды простых чисел были числами Мерсенна, потому что существует алгоритм проверки того, является ли число вида 2^p – 1 простым (тест Люка — Лемера).