Сразу же отметим, что в 1938 г. Нильс Пиппинг «вручную» проверил бинарную гипотезу Гольдбаха для всех четных чисел вплоть до 100000 [1].
Сразу после «двойки» идёт чётное число 4, которое представляется как сумма двух простых:
4 = 2 + 2, т.е. для «четвёрки» Гипотеза выполняется. Идём дальше…
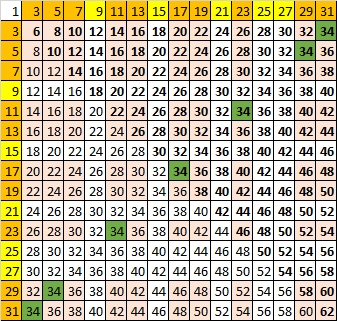
Построим таблицу попарных сумм нечётных чисел, в которой простые и нечётные составные числа выделены своими цветами, следующим образом:

Как видим, в таблице «сидят» все чётные числа от 6 до 62. При этом, все числа, кроме «шестёрки» (и «восьмёрки», которая представлена двумя экземплярами только из-за перестановки слагаемых «3» и «5»), представлены несколькими экземплярами и расположены они строго параллельно большой диагонали, идущей от левого нижнего угла в правый верхний и выделенной зелёным цветом.
А теперь, несколько видоизменим таблицу, а именно, выделим чётные числа, образованные суммой только простых чисел. Вот новая таблица:

Итак, несмотря на то, что чётные числа, полученные суммированием с участием составных нечётных чисел «вырезали» хорошие «куски» из нашей таблицы, мы всё ещё можем набрать последовательность от 6 до 62, удовлетворяющую Гипотезе.
Понятно, что с продолжением последовательности нечётных чисел, суммы с участием составных будут «вырезать» всё бoльшие «куски», не удовлетворяющие Гипотезе. В итоге, чтобы доказать Гипотезу, нам надо опровергнуть возможность ситуации, изображённой в новой таблице.

А изображено здесь следующее: «после простого числа Pn следующим простым числом является число Pn+1 > 2•Pn (n – номер простого числа в последовательности простых чисел, начиная с двух)»…
Приступаю к опровержению. Итак, нам надо доказать, что для любого простого числа Pn в интервале от Pn до 2•Pn имеется, по крайней мере, следующее простое число Pn+1.
А доказывать, оказывается, уже ничего не нужно, потому что это утверждение — доказанный постулат Бертрана.
Литература
- Стюарт И. Величайшие математические задачи / Иэн Стюарт; Пер. с англ. — М.: Альпина нон-фикшн, 2015.— 460с.
- Выгодский М.Я. Справочник по элементарной математике. – Изд. 27-е, испр.- М.: Наука. Главная редакция физико-математической литературы, 1986. – 320с.
Комментарии (21)

pohjalainen
02.12.2018 17:55+3Ваше выделенное жирным утверждение — это хорошо известный и доказанный постулат Бертрана. Проблема в том, что гипотеза Гольдбаха из него не следует.
Ну и ваше доказательство доказательством не является, это лишь эмпирическая проверка до 121.
Вот это «с подключением нового простого числа Pn реализуются новые «расстояния» как сумма пар некоторых, уже реализованных «расстояний»» — нужно строго доказать.
Newton2 Автор
02.12.2018 18:20Да, пытаясь сократить текст, я, похоже, убрал некоторые нужные подробности. Постулат Бертрана надо увязать со второй таблицей. «Изюминка» этой таблицы в том, что, в отличие от приведённой у Стюарта, она построена для всех нечётных чисел и явно прослеживается закономерность. А в таблице, приведённой у Стюарта, для построения таблицы использованы только простые числа и никакой закономерности не прослеживается и он дальше начинает говорить про вероятности…
А насчёт «с подключением нового простого числа Pn реализуются новые «расстояния» как сумма пар некоторых, уже реализованных «расстояний» может надо было так изложить:
Каждое новое ещё не вычеркнутое число делит участок с составными числами на две части, а когда это число будет вычеркнуто, то объединит эти части. По-моему, вполне доказательное утверждение.
Temmokan
03.12.2018 06:28Почему бы не привести для начала строгое доказательство того, что если эта гипотеза справедлива для Pn, то она будет справедлива и для Pn+1?

DjSapsan
03.12.2018 12:43Похоже вы просто интерполируете известное на неизвестное. Но формальное доказательство требует полной цепочки рассуждений. А вы смотрите на формальную систему снаружи, как бы «заранее зная» результат, без его вывода.

pohjalainen
03.12.2018 15:04+2Извините, но это невозможно читать. Изюминка, подключение, реализуются, прослеживается… Вы используете эти слова так, что смысл понятен только вам. И даже сейчас вы ничего не доказали. Опишите алгоритмически процедуру вычеркиваний, объединений и т.д., и вы сами увидите ошибку.

Newton2 Автор
04.12.2018 20:26Описываю алгоритмически процедуру вычеркиваний, объединений и т.д.:
1. Первая таблица показывает (нет, доказывает), что суммы пар нечётных чисел образуют непрерывные последовательности чётных чисел, как по горизонтали, так и по вертикали. При этом, экземпляры каждого чётного числа расположены строго по диагонали, идущей слева снизу вправо вверх. Нет никаких аргументов, что с продолжением таблицы на бОльшие числа, что-то изменится в этой структуре.
2. Вторая таблица отличается от первой тем, что в ней выделены розовым чётные числа, образованные суммированием только простых чисел. Так как, выделения образованы вертикалями и горизонталями («уголками»), то они пересекают диагонали, образованные экземплярами каждого чётного числа. И пока, не появится «зазор-уголок», образованный составными числами, который вместит в себя все экземпляры хотя бы одного чётного числа (зелёная диагональ в таблице 3), мы можем «собрать» непрерывную последовательность чётных чисел из выделенных (розовых) клеточек. Т.е. любое чётное число может быть представлено как сумма двух простых,
если Pn+1 < 2•Pn для любого n (большего, чем уже проверенные).
3. Вы сами отметили, что выделенное мной утверждение — доказанный постулат Бертрана, т.е. мне уже дальше ничего доказывать не нужно. Не «порванных» зелёных диагоналей не существует.
Sirion
05.12.2018 00:38Это называется «доказательство измором». Постить всякую дичь, пока оппонентам не надоест указывать на дыры. Потом объявить себя победителем.
Правда, в случае публикации в рецензируемых научных журналах это почему-то не работает. Поэтому и приходится постить на хабр, да?)

Mikluho
05.12.2018 07:26Вот бы ещё это прочитать на русском (у вас какой-то другой язык), да с нормальной математикой (зазор-уголок — это просто фантастика!)…
Понять, что у вас написано, мне не получилось, но есть встречное предложение.
Вот такая же табличка, но более внятно покрашенная:
Не уверен, что вы хотели сказать именно это, но искомое число следует искать в зелёных клеточках. Я тут белым покрасил всё, что содержит непростые числа. Жирным выделена одна половина таблицы (во второй те же комбинации).
Собственно, ваше доказательство строится на том, что в для искомого числа всегда найдётся зелёная клеточка?

iliazeus
02.12.2018 18:20Можете, пожалуйста, подробнее пояснить, как из Pn+1 <= 2Pn следует гипотеза Гольдбаха?

third112
02.12.2018 19:29Доказательство. Сразу же отметим, что в 1938 г. Нильс Пиппинг «вручную» проверил бинарную гипотезу Гольдбаха для всех четных чисел вплоть до 100000 [1].
Грубая методологическая ошибка! Отмеченный факт не является необходимым для доказательства. Всему, что не явлеется необходимым, не место в доказательстве! Между словами «Доказательство» и «Доказательство завершено.» должны быть только совершенно необходимые вещи! Считаете нужным что-то отметить — Ваше право: отмечайте ДО или ПОСЛЕ доказательства.

MiXei4
02.12.2018 20:06+1Почему во второй таблице, в строке с числом 9, например, есть как белые, так и розовые ячейки?

Temmokan
03.12.2018 06:26В качестве мелкой придирки:
Второй проход, накладываясь на первый, устанавливает два чередующихся «расстояния» равные 2 и 4, но уже не просто между нечётными числами, а между нечётными «подозрительными» на «простоту»…
Второй проход — это удаление всех кратных 3. Какие 2 и 4, простите?
Эти закономерности и доказывают
С какого перепуга доказывают? Проверили на нескольких первых простых числах, и считаем, что дальше будет ровно то же? А потом на этом (не доказанном строго) утверждении строим всё прочее?
Напоминает «физическое доказательство» о том, что все числа — простые, из «Физики продолжают шутить».

gul_kiev
04.12.2018 20:32У вас раскраска таблицы неправильная (или я не понял).
Например, 20 как 9+11 покрашена розовым (как сумма двух простых), хотя должна быть белой из-за девятки.


altrus
Хотя на Хабре могут…
KvanTTT
Ну это вы все-таки не уважаете аудиторию хабра.