Как известно, Проблема четырёх красок решена в результате перебора вариантов на компьютере. Но не все математики согласны с таким решением, поскольку возникают сложности с проверкой отсутствия ошибок.

Для непосвящённых… Проблема четырёх красок формулируется очень просто: «Для раскраски любой карты на плоскости достаточно четырёх красок».

При этом, если области (страны) «касаются» только в одной точке, то считается, что они не граничат и их можно раскрасить в один и тот же цвет. Так, например, для раскраски клеток шахматной доски достаточно двух цветов.

Более того, Мартин Гарднер в книге «Математические головоломки и развлечения» упоминает, что доказана теорема «о двухцветных картах», которая утверждает, что «любую карту на плоскости можно раскрасить в два цвета тогда и только тогда, когда все её вершины чётны» (здесь, «вершиной» называется точка, в которой сходятся границы более двух стран).

* * *

Создал очень НЕинтересную игру, навеянную этой Проблемой.

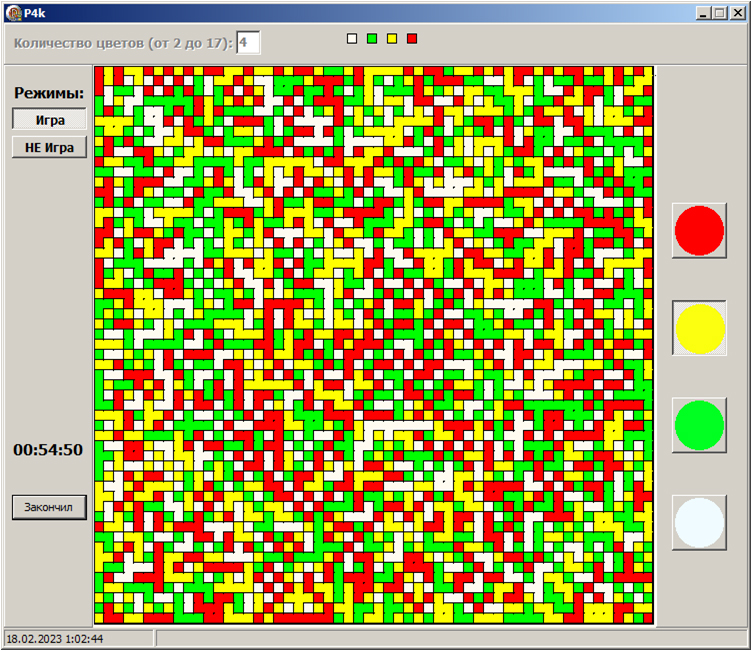
Поле для игры

Области образованы из квадратиков (клеток) первоначальной сетки (56х55), из которой убраны некоторые звенья, т.е. границами областей являются замкнутые ломаные линии, каждое звено которой повёрнуто относительно соседней на угол кратный 90°.

Если области имеют единственную общую точку (узел сетки), то они считаются не граничащими между собой и могут быть окрашены в один и тот же цвет. Поскольку, изначально сетка квадратная, то в одной точке могут сходиться четыре области и тогда (если другие границы с другими областями позволят) эти четыре области могут быть раскрашены в два цвета как клетки шахматной доски (см. Рис.1а).

Также легко имитируется схождение трёх областей в одной точке, ввиду того что, в этом случае, каждая из этих областей обязательно граничит с двумя другими (см. Рис.1б). Следовательно, здесь обязательно потребуется три цвета для правильной раскраски.

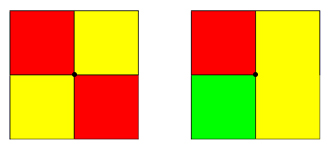
а) б) Рис.1

Правила игры

1. Нужно раскрасить в 4 цвета карту, в которой разбиение на области (страны) произведено случайным образом при помощи стандартного генератора случайных чисел.

2. Предлагается использовать цвета: красный, жёлтый, зелёный и кремовый (clCream, который на моём мониторе выглядит, практически, как чисто белый).

3. Есть условие, что, окаймляющая карту, область закрашена в кремовый цвет и, соответственно, все области, граничащие с краями карты (периметр карты), должны быть раскрашены строго в три других цвета.

4. Работает таймер, который останавливается при «нажатии» кнопки «Закончил». После этого производится проверка правильности раскраски и если есть ошибка, указываются её координаты. По подтверждению игроком прочтения этого сообщения, таймер включается для продолжения отсчёта затраченного времени.

5. Формируется и хранится список одиннадцати лучших результатов.

*

Нюансы реализации Программы

Для существования решения (способа раскраски карты) поле игры формируется следующим образом (в тайне от игрока).

Поле размечается сеткой с квадратными ячейками. Затем, случайным образом разыгрывается цвет каждой ячейки.

На следующем шаге, ячейки одного цвета, имеющие общую границу, объединяются путём удаления этой общей границы. В результате, получаются области, ограниченные замкнутыми ломаными линиями и раскрашенные в 4 цвета.

Для обеспечения пункта 3 Правил игры, вначале производится раскраска ячеек по периметру карты в три цвета и только потом раскрашиваются внутренние ячейки в четыре цвета.

И, наконец, все области перекрашиваются в цвет clCream и карта предъявляется игроку.

*

Программа имеет два режима: «Игра» и «НЕ Игра».

Про первый режим рассказано выше. Второй режим предоставляет некоторые возможности для экспериментирования. Так, можно выбрать количество цветов для исходной раскраски в пределах от 2 до 18. Тем не менее, задача остаётся той же самой – раскрасить в 4 цвета (или меньшее количество цветов, если выбрана двухцветная или трёхцветная карта).

Выдаётся отчёт по параметрам созданной карты.

Отсчёт времени не ведётся.

Исходная раскраска карты демонстрируется.

*

Мои наблюдения в режиме «НЕ Игра»

1. Увеличение количества цветов раскрашивания ведёт к упрощению формы областей, поскольку ячейки одинакового цвета реже оказываются рядом и, соответственно, уменьшается среднее количество ячеек в областях. Больше становится «шахматных досок», которые раскрашиваются в два цвета.

2. С раскраской «пятицветной» карты в четыре цвета проблем не было (тем более, если цветов ещё больше, то и карта проще для раскраски).

3. При ошибочной окраске какой-либо области обычно для исправления достаточно перекраски двух-трёх ближних областей.

4. Ошибочная раскраска, требующая исправлений, бывает редко, чаще бывают пропущенные «одноклеточные» области (из-за большой площади игрового поля).

5. Очень часто встречается возможность выбора из двух цветов для конкретной области. Т.е., вероятность того, что ваша раскраска совпадёт с исходной, практически, равна нулю (кроме, конечно, раскраски в два цвета, когда условие 3 Правил игры однозначно определяет цвета раскраски).

Ещё про двухцветную раскраску

Чтобы выполнялось условие чётности всех вершин в «теореме о двухцветной карте», необходимо, чтобы карта занимала всю плоскость. Иначе, надо оговаривать, что цвет, «окаймляющей» карту, области ,не участвует в задаче (при её «участии» условие «чётности всех вершин» невыполнимо). То есть, получается мы рассматриваем не всю бесконечную плоскость, а только её некоторый конечный участок.

Не в этом ли кроется сложность доказательства Теоремы четырёх красок?

Например, для поверхности тора смогли доказать, что для раскраски любой карты достаточно семи красок. А поверхность тора конечна...

Кстати, достаточно ли обосновано утверждение о том, что «поверхность сферы с одной выколотой точкой топологически эквивалентна плоскости»? С одной стороны, «выкалывание» точки нарушает целостность поверхности сферы, что, вроде, недопустимо в топологии. С другой стороны, поверхность сферы конечна в отличие от плоскости…

Учёт, «окаймляющей» карту, области сразу накладывает ограничение. Если даже в карте все вершины чётные, то окаймляющая область может быть окрашена только в третий цвет. А для карты, все вершины которой нечётные, окаймляющая область может быть окрашена только в четвёртый цвет. Это видно и на наших рисунках (Рис.1а и б).

*

Желающим могу выслать исходники на Delphi. Пишите в личку.