Что такое шум Перлина?

Шум Перлина придуман в 1983 году Кеном Перлином (получившим за это достижение премию Американской Академии кинематографических искусств и наук). Видите ли, в те времена все стремились к фотореализму, но его всегда не хватало. Кен Перлин придуман этот алгоритм шума, чтобы избавиться от жалкого «компьютерного» внешнего вида 3D-моделей. Шум — это генератор случайных чисел в компьютерной графике. Это случайный неструктурированный паттерн, он полезен в тех случаях, когда требуется источник подробных деталей, недостающих в очевидной структуре¹. Шум Перлина — это многомерный алгоритм, используемый в процедурной генерации, текстурах, генерации рельефа, генерации карт, генерации поверхностей, генерации вершин, и так далее, и тому подобное. В таблице ниже² показаны пределы возможностей шума Перлина:

Размерность	Сырой шум (градации серого)	Применение
1		Векторные объекты, выглядящие нарисованными от руки
2		Такие объекты, как процедурные текстуры и пламя
3		Шум Перлина используется в рельефе Minecraft

Перлин дал следующее определение шума: шум — это аппроксимация к белому шуму, ограниченная по диапазону одной октавой³. Формальное определение шума имеет следующий вид:

$$

Где $$ — функция шума. Шум Перлина — это процедурный шум. «Прилагательное процедурный используется в компьютерных науках, чтобы отделить сущности, описываемые программным кодом, от описываемых структурами данных»⁴. То есть нечто сгенерированное, а не заданное жёстко. Что хорошего в использовании процедурного шума вместо, например, создания шума вручную? Процедурный шум компактен, то есть занимает меньше места. Он неразрывен, то есть апериодичен. Он параметрический, к нему можно получать произвольный доступ; также он имеет много других достоинств, упрощающих жизнь художника… А разве это не конечная наша цель — служить художнику? Вчера я создал плагин для After Effects, который можно увидеть в моём предыдущем посте. Я не учитывал в нём интересы художника, только интересы своего эго, поэтому никто его не скачивал. Я понял урок: служи художнику, а не самому себе.

До Перлина появились шумы градиентов решёток. Они генерировались интерполяцией между случайными значениями, а в шуме Перлина для каждой вершины используется кубическая решётка, а затем выполняется сплайновая интерполяция. «Псевдослучайный градиент получается хешированием точки решётки и использованием результата для выбора градиента»⁵. Эти хеши превращаются в 12 векторов и интерполируются от центра к краям с помощью многочлена пятой степени. Это сложновато представить, правда? Не волнуйтесь. Я покажу это на изображениях⁶ и в псевдокоде⁷.


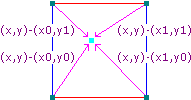
"… интерполируются от центра к краям с помощью многочлена пятой степени"

А вот псевдокод классического Перлина без хеш-функции:

// Function to linearly interpolate between a0 and a1
// Weight w should be in the range [0.0, 1.0]
float lerp(float a0, float a1, float w) {
    return (1.0 - w)*a0 + w*a1;

    // as an alternative, this slightly faster equivalent formula can be used:
    // return a0 + w*(a1 - a0);
}

// Computes the dot product of the distance and gradient vectors.
float dotGridGradient(int ix, int iy, float x, float y) {

    // Precomputed (or otherwise) gradient vectors at each grid node
    extern float Gradient[IYMAX][IXMAX][2];

    // Compute the distance vector
    float dx = x - (float)ix;
    float dy = y - (float)iy;

    // Compute the dot-product
    return (dx*Gradient[iy][ix][0] + dy*Gradient[iy][ix][1]);
}

// Compute Perlin noise at coordinates x, y
float perlin(float x, float y) {

    // Determine grid cell coordinates
    int x0 = int(x);
    int x1 = x0 + 1;
    int y0 = int(y);
    int y1 = y0 + 1;

    // Determine interpolation weights
    // Could also use higher order polynomial/s-curve here
    float sx = x - (float)x0;
    float sy = y - (float)y0;

    // Interpolate between grid point gradients
    float n0, n1, ix0, ix1, value;
    n0 = dotGridGradient(x0, y0, x, y);
    n1 = dotGridGradient(x1, y0, x, y);
    ix0 = lerp(n0, n1, sx);
    n0 = dotGridGradient(x0, y1, x, y);
    n1 = dotGridGradient(x1, y1, x, y);
    ix1 = lerp(n0, n1, sx);
    value = lerp(ix0, ix1, sy);

    return value;
}

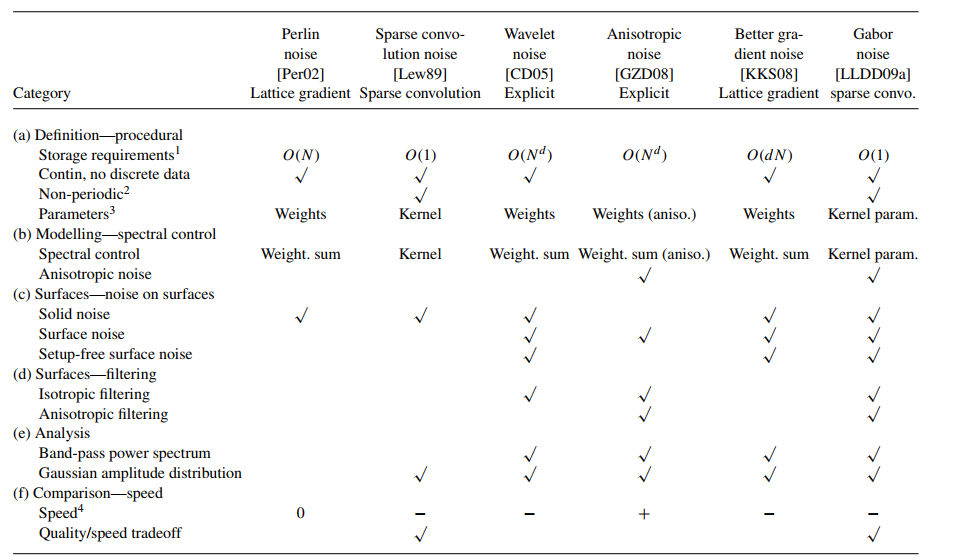
Стоит также знать, что «все функции шума, кроме шума Перлина и шума разреженной свёртки приблизительно полосовые. Шум Перлина лишь слабополосовой, что может приводить к проблемам с искажениями и утерей деталей»⁸. Кроме того, у шума Перлина нет гауссова распределения амплитуд. То есть пятна шума не рассеиваются на основании гауссовой функции, которую мы в этой статье рассматривать не будем. Существует множество вещей, в который Перлин очень удобен, но есть и вещи, в которых он очень слаб. В таблице ниже⁹ вы можете увидеть это самостоятельно.

Шум Перлина на практике: реализации на GLSL

Итак, поговорим о шуме Перлина на GLSL. Шум Перлина можно использовать как волну, как диффузный цвет, как диффузный материал, как мерцающий свет, или как пятна на текстуре. Лично я использовал его в данном примере как мерцание цвета.


В процессе написания этой статьи я размышляю над созданием плагина для After Effects, добавляющего функционал шума Перлина.

Простейший шум Перлина можно создать¹⁰ следующим образом:

float rand(vec2 c){
	return fract(sin(dot(c.xy ,vec2(12.9898,78.233))) * 43758.5453);
}

float noise(vec2 p, float freq ){
	float unit = screenWidth/freq;
	vec2 ij = floor(p/unit);
	vec2 xy = mod(p,unit)/unit;
	//xy = 3.*xy*xy-2.*xy*xy*xy;
	xy = .5*(1.-cos(PI*xy));
	float a = rand((ij+vec2(0.,0.)));
	float b = rand((ij+vec2(1.,0.)));
	float c = rand((ij+vec2(0.,1.)));
	float d = rand((ij+vec2(1.,1.)));
	float x1 = mix(a, b, xy.x);
	float x2 = mix(c, d, xy.x);
	return mix(x1, x2, xy.y);
}

float pNoise(vec2 p, int res){
	float persistance = .5;
	float n = 0.;
	float normK = 0.;
	float f = 4.;
	float amp = 1.;
	int iCount = 0;
	for (int i = 0; i<50; i++){
		n+=amp*noise(p, f);
		f*=2.;
		normK+=amp;
		amp*=persistance;
		if (iCount == res) break;
		iCount++;
	}
	float nf = n/normK;
	return nf*nf*nf*nf;
}

#define M_PI 3.14159265358979323846

float rand(vec2 co){return fract(sin(dot(co.xy ,vec2(12.9898,78.233))) * 43758.5453);}
float rand (vec2 co, float l) {return rand(vec2(rand(co), l));}
float rand (vec2 co, float l, float t) {return rand(vec2(rand(co, l), t));}

float perlin(vec2 p, float dim, float time) {
	vec2 pos = floor(p * dim);
	vec2 posx = pos + vec2(1.0, 0.0);
	vec2 posy = pos + vec2(0.0, 1.0);
	vec2 posxy = pos + vec2(1.0);
	
	float c = rand(pos, dim, time);
	float cx = rand(posx, dim, time);
	float cy = rand(posy, dim, time);
	float cxy = rand(posxy, dim, time);
	
	vec2 d = fract(p * dim);
	d = -0.5 * cos(d * M_PI) + 0.5;
	
	float ccx = mix(c, cx, d.x);
	float cycxy = mix(cy, cxy, d.x);
	float center = mix(ccx, cycxy, d.y);
	
	return center * 2.0 - 1.0;
}

// p must be normalized!
float perlin(vec2 p, float dim) {
	
	/*vec2 pos = floor(p * dim);
	vec2 posx = pos + vec2(1.0, 0.0);
	vec2 posy = pos + vec2(0.0, 1.0);
	vec2 posxy = pos + vec2(1.0);
	
	// For exclusively black/white noise
	/*float c = step(rand(pos, dim), 0.5);
	float cx = step(rand(posx, dim), 0.5);
	float cy = step(rand(posy, dim), 0.5);
	float cxy = step(rand(posxy, dim), 0.5);*/
	
	/*float c = rand(pos, dim);
	float cx = rand(posx, dim);
	float cy = rand(posy, dim);
	float cxy = rand(posxy, dim);
	
	vec2 d = fract(p * dim);
	d = -0.5 * cos(d * M_PI) + 0.5;
	
	float ccx = mix(c, cx, d.x);
	float cycxy = mix(cy, cxy, d.x);
	float center = mix(ccx, cycxy, d.y);
	
	return center * 2.0 - 1.0;*/
	return perlin(p, dim, 0.0);
}

Однако это переделанная версия шума Перлина, которая создана в 2002 году. Перейдите в Gist, чтобы увидеть, как реализуется классический шум Перлина.

Ну, вот и всё на сегодня. Короткий пост, я знаю, и в нём не хватает оригинального контента, но пока у меня заканчиваются идеи, потому что я пока не прочитал Real-Time Rendering. В этой книге полно концепций и идей для изучения и обучения. Обожаю её!


Параллельно я читаю ещё одну книгу — Fundamentals of Computer Graphics. Я немного застрял на теме косвенных кривых (Implicit Curves), но попрошу своего родственника с PhD по математике помочь мне.

Справочные материалы

• A Survey of Procedural Noise Functions, Computer Graphics Forum, Volume 29 (2010), Number 8, pp 2379-2600
• Efficient Computational Noise, Journal of Graphics Tools Volume 16, No. 2: 85-94

1. A Survey, et al
2. flafla2.github.io/2014/08/09/perlinnoise.html
3. A. Lagaue et al
4. A. Lagae, et al
5. A. Lagae, et al
6. Из flafla2.github.io/2014/08/09/perlinnoise.html
7. Из Википедии
8. A. Lagae, et al
9. Взято из A. Lagae, et al
10. gist.github.com/patriciogonzalezvivo/670c22f3966e662d2f83