26.03.2019 14:22
Tzimie 50 16200 Источник
О математике (так, чтобы было интересно) писать сложнее, чем о физике. Однако я надеюсь, что вы дочитаете хотя бы до примеров сумасшедших программ на C.

image

Из совершенно безобидных вещей могут вырастать монстры. Возьмем, например, игру в substrings. Напишем строку из букв a и b и выделим подстроки с символа 1 до символа 2, с 2 до 4, с трех до 6, с n до 2n, пока хватит длины основной строки. Наша задача сделать так, чтобы в этих подстроках более короткая не входила в любую более длинную. Я даже написал анализатор на SQL:

declare @s varchar(max) = 'abbbaaaaaaab'
declare @n int=1
declare @sub table (n int, sub varchar(max)) 
while @n*2<=len(@s) begin
  insert into @sub select @n,substring(@s,@n,@n+1)
  set @n=@n+1
  end
select *,(select max(sub) from @sub I where I.n>O.n 
  and charindex(O.sub,I.sub)>0) as FoundMatch
  from @sub O order by 1

Вот пример вывода:



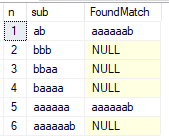
Как видно, подстроки 1 и 5 не прошли проверку. Мы можем убрать последний символ, и получившаяся строка из 11 символов 'abbbaaaaaaa' проверку пройдет. Оказывается, что это и самая длинная возможная строка в алфавите из двух символов, которая удовлетворяет данному условию.

Для алфавита из одного символа максимальная длина строки равна 3, и то по чисто техническим соображениям. Оказывается, максимальная длина конечна для алфавита из любого количества букв. Итак, мы имеем:

$f(1) = 3 $

$f(2) = 11 $

$f(3) = ??? $


Проверьте свою интуицию, какой длины строку можно соорудить в алфавите из трех букв. 100? 1000? На самом деле много больше, чем Гугол, и много больше, чем ГуголПлех.

$f(3) > 2 \uparrow^{7198} 158836$


И мне придется потратить время, чтобы показать силу стрелок.

Стрелки (гипероперации)


Мы используем умножение, чтобы не писать много операций сложения:

$2*5 = 2 + 2 + 2 + 2 + 2$

Мы используем возведение в степень, чтобы не писать много умножений:

$2^3 = 2 * 2 * 2$

Считая сложение операцией уровня 0, умножения — 1, возведения в степень — 2, мы можем ввести операцию «стрелка», например,

$3 \uparrow 3 = 3^{(3^3)} = 3^{27} = 7'625'597'484'987$

Обратите внимание, что здесь уже важны скобки. Следующим уровнем является операция две стрелки:

$3 \uparrow \uparrow 3 = 3 \uparrow (3 \uparrow 3) = 3 \uparrow 7625597484987 = 3^{3^{...^3}}$

Последняя пирамида троек имеет в высоту 7 биллионов, и это число уже намного, намного больше и гугола и гуголплекса. Обозначим это огромное число как Тьма (было такое числительное в старом русском языке) и попробуем сделать еще один шаг:

$3 \uparrow^3 3 = 3 \uparrow \uparrow \uparrow 3 = 3 \uparrow \uparrow (3 \uparrow \uparrow 3) = 3 \uparrow \uparrow {тьма} = 3 \uparrow 3 \uparrow 3 ... \uparrow 3$

(и так тьма раз)… Тут уже даже представить, сколь велико это число. Обратите внимание, что когда стрелок много, мы пишем повторитель вверху. Так что вы можете понять, сколь велико

$f(3) > 2 \uparrow^{7198} 158836$


И еще больше


С помощью стрелок создаются лишь самые маленькие из больших чисел, если так можно сказать. Скорость роста функций измеряется по некоей шкале — путем сравнения со быстрорастущими функциями. Первая функция в этой иерархии соответсвует сложению, вторая — умножению, третья — стрелке, n-ная — n-2 стрелкам (приблизительно, не точно). Но можно определить

$f_w (n) = f_n(n)$

Такая функция для для n=3 сравнима с одной стрелкой, для n=4 с двумя стрелками, а при росте параметра n опережает рост функии с любым статическим количеством стрелок.

Можно пойти еще дальше: $f_w, f_{w+1}, f_{w+n}, f_{w2}, f_{w^2}, f_{w^w}, f_{w^{w^{w}}}, f_\epsilon$Функции эти индексируются ординалами, или в русской литературе — порядковыми числами. Картинка со структурой начальных порядковых чисел предваряет статью, но они простираются куда дальше, и дальше начинается

Небольшая мистика


Бесконечная пирамида из 'омег' дает некий ординал $\epsilon_0$. Почитайте про функцию, рост которой измеряется этим ординалом. Выясняется, что функция растет так быстро, что формальная арифметика не может в принципе доказать, что такая функция вообще определена!

Вы, конечно, знаете про теорему Геделя, что есть недоказуемые утверждения. Но, как правило, единственный пример такого утверждения, это само построение Геделя («я недоказуемо»). Теорема Goodstein — хороший пример такого утверждения.

Более того, оказывается, что ординалы неким образом измеряют силу теорий. 'Сила' формальной арифметики равна $\epsilon_0$, упрощенная теория множеств Крипке-Платека имеет силу ординала Фефермана-Шутте итд.

Жесть — Математики жгут — Соревнование на языке C


Было проведено соревнование по генерации больших чисел. Нет, программирование для машины Тьюринга — это все-таки слишком жестоко, поэтому использовался язык C для некоей абстрактной бесконечной машины, у которой sizeof(int)=бесконечности. Можно также было использовать malloc(), причем объем памяти, как и стека, не ограничен. Ограничена была лишь длина программы — программа должна была укладываться в 512 байт (без учета пробелов), но допускалось использование препроцессора (#define).

Результаты опубликованы на сайте математика. Заодно зацените дизайн сайта настоящего математика. Результаты тут. Вот текст программы, занявшей второе место, дающей число около

$f_{w^w}(10^{500})$



typedef int	J;
J P(J x,J y)	{ return x+y ? x%2 + y%2*2 + P(x/2,y/2)*4 : 0 ;}
J H(J z)	{ return z ? z%2 + 2*H(z/4) : 0 ;}
J I(J f,J e,J r){ return f ? P(P(f,e),r) : r ;}
J M(J x,J e)	{ return x ? I(x%2, M(e,0), M(x/2, e+1)) : 0 ;}
J D(J,J);	 
J E(J f,J e,J r,J b)
{
    return e ? E(1, D(e,b), I(b-1, D(e,b), I(f-1,e,r)), b) : I(f-1,e,r) ;
}
J D(J x,J b)	{ return x ? E( H(H(x)), H(H(x)/2), H(x/2), b) : 0 ;}
J F(J x,J b)	{ return x ? F(D(x,b+1),b+1) : b ;}
J G(J x)	{ return F(M(x,9), 9) ;}
J f(J n,J x)	{ return n ? f(n-1, G(x ? f(n,x-1) : n)) : G(x) ;}
J g(J x)	{ return f(x,x) ;}
J h(J n,J x)	{ return n ? h(n-1, g(x ? h(n,x-1) : n)) : g(x) ;}
J main(void)	{ return h(g(9),9) ;}

Текст программы победителя более длинен, я просто хотел показать, с чего он начинается:

#define R { return
#define P P (
#define L L (
#define T S (v, y, c,
#define C ),
#define X x)
#define F );}

Но оценить, насколько большое число получилось, затруднился даже организатор конкурса (написано very big)

Busy Beavers


Ладно, хватит заниматься крошечными числами, займемся большими. Представьте, что организован вселенский конкрус на написание программы по генерации самого большого числа. Так как число программ не длиннее 512 символов конечно, обязательно есть абсолютный победитель. Обозначим его как BB(512) — busy beaver function.

Ясно, что BB(1024) >> BB(512). Но как быстро растет сама функция BB? Оказывается, она растет быстрее чем все, с чем мы встречались. Сама функция BB алгоритмически неразрешима, ее нельзя рассчитать на компьютере. Но при увеличении длины допустимой программы мы можем реализовать все больше и больше новых идей. Так что BB растет быстрее, чем любая алгоритмически разрешимая функция.

BIG FOOT


Ладно, хватит заниматься крошечными числами, займемся большими. Ах, я это уже говорил? Было бы классно запустить BB(BB(n)). Но так как BB невычислима, с этим есть технические сложности (такая функция вычислима в машинах Тьюринга с оракулами — не путать орАкулов с СУБД Оракл).

Но можно поступить проще, вместо программы рассмотреть формулу с кванторами длины n. Формуле с кванторами не важно, вычислимо что-то или нет. Так можно хоть взять функцию BB(10000000000), и применять ее к себе BB(BB(BB(1000000))) раз. И это только то, что первым пришло в голову.

Самое большое число, которое можно обозначить формулой не более n символов, обозначается FOOT(n).

$BIG FOOT = FOOT^{10}(10^{100})$



P.S.


Для следующей статьи хотелось бы понять, на что ориентироваться, поучаствуйте в опросе пожалуйста

Комментарии (50)


  1. NeoCode
    26.03.2019 17:45
    #19945594

    И ведь все эти немыслимо огромные числа — ничто по сравнению с Бесконечностью…


    1. Tzimie Автор
      26.03.2019 17:45
      #19945598
      +3

      Да, а бесконечностей — куча разных типов


      1. KvanTTT
        26.03.2019 18:29
        #19945806

        Куча? Я знаю два: счетную и несчетную. Об этом, собственно, говорится в Континуум-гипотезе.


        1. Tzimie Автор
          26.03.2019 18:33
          #19945836
          +3

          Если принять континуум гипотезу, то счетная это алеф ноль, континуум это алеф 1, ну а дальше они индексируются ординалами, например, алеф омега)


          1. KvanTTT
            26.03.2019 21:44
            #19946618

            Ну тогда интересно будет об этом почитать в одной из следующих ваших статей :)


            1. perevedko
              27.03.2019 01:30
              #19947400

              How To Count Past Infinity


              1. Tzimie Автор
                27.03.2019 11:04
                #19948764

                Да, это было хорошее видео


          1. vesper-bot
            27.03.2019 13:39
            #19949724

            Я знаю только про алеф-два — множество всех однозначных функций от одного аргумента, и в принципе догадывался, что их можно посчитать, с учетом формулы «алеф-один равен 2^алеф-ноль», но представить себе, нафига, так и не могу.


            1. 0xd34df00d
              27.03.2019 14:58
              #19950124
              +1

              Математика не задаётся вопросом «нафига».


        1. masai
          26.03.2019 20:53
          #19946474

          В континуум-гипотезе говорится, что континуум — наименьшая, превосходящая мощность счётного множества. Но не говорится, что нет других.


          Например, мощность множества функций R>R больше мощности множества R.


        1. 0xd34df00d
          27.03.2019 00:41
          #19947282

          А вам бесконечности с порядком или без?

          Если без, то возьмите множество функций из несчетной бесконечности в {0, 1}, и так далее.

          Если с, то там вообще все ппц интересно, даже неизоморфных счётных бесконечностей минимум счетное число.


          1. Cerberuser
            27.03.2019 05:15
            #19947586

            Речь про разницу между кардиналами и ординалами, если я правильно понимаю?


            1. 0xd34df00d
              27.03.2019 14:57
              #19950120

              Да.


        1. polsok
          29.03.2019 08:37
          #19957994

          Если мы постулируем такую идею как бесконечность, почему бы не предположить что её существует бесконечность типов? Во всяком случае пока не доказано обратное


          1. Tzimie Автор
            29.03.2019 09:54
            #19958244

            Бесконечностей куда больше, чем бесконечность)


            1. Cerberuser
              29.03.2019 10:20
              #19958368

              Чем первая из бесконечностей или чем любая из них?


              1. Tzimie Автор
                29.03.2019 10:34
                #19958428

                Как минимум больше чем первая.


      1. maxzhurkin
        26.03.2019 19:02
        #19945996

        Если вы про мощности множеств, то гипотетически только две — счётная и континуальная


        1. Tzimie Автор
          26.03.2019 19:04
          #19946008
          +3

          Хехе. Их куда больше


          1. maxzhurkin
            26.03.2019 19:05
            #19946016

            «Их» — это кого?


            1. Tzimie Автор
              26.03.2019 19:07
              #19946022
              +2

              Разных мощностей


              1. maxzhurkin
                26.03.2019 19:10
                #19946040

                Есть решение первой проблемы Гильберта?


                1. Tzimie Автор
                  26.03.2019 19:13
                  #19946052
                  +3

                  Нет, проблема Гильберта это лишь о том, существуют ли мощности МЕЖДУ счетной и континуумом. Операция powerset() /множество всех подмножеств/ всегда создает мощность больше, чем исходная. можно создавать сколь угодно большие мощности.


                  1. maxzhurkin
                    26.03.2019 19:16
                    #19946062

                    А где можно почитать про мощности больше континуальной?
                    Или как загуглить?
                    P.S. кстати, чем не тема для статьи?


                    1. Tzimie Автор
                      26.03.2019 19:25
                      #19946098
                      +2

                      Я напишу
                      Там все ОЧЕНЬ интересно


                      1. maxzhurkin
                        26.03.2019 19:34
                        #19946142

                        Не сомневаюсь: некоторое время назад пытался разобраться с этим вопросом самостоятельно и не смог, при том, сломался уже на поиске, то есть, найденный материал, вроде бы как и был понятен, но то ли не проливал свет на вопрос, то ли я его неправильно понимал


                        1. fesst
                          27.03.2019 18:44
                          #19951372

                          Например,
                          ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%80%D1%8F%D0%B4%D0%BA%D0%BE%D0%B2%D0%BE%D0%B5_%D1%87%D0%B8%D1%81%D0%BB%D0%BE


                          1. maxzhurkin
                            27.03.2019 19:30
                            #19951546

                            Сюда я или не попал, или упустил связь с мощностью множеств


                            1. Tzimie Автор
                              27.03.2019 20:09
                              #19951734

                              Она двоякая
                              Я напишу об этом


                    1. weedjy
                      26.03.2019 22:39
                      #19946854

                      Некоторое время назад с большим интересом посидел на курсе Paradox and Infnity от MIT (https://www.edx.org/course/paradox-infinity-mitx-24-118x-0). Сейчас он заархивирован, но, возможно, повторят. Разных бесконечностей бесконечно много и описываются они чем-то вроде итерационного процесса, который можно продолжать бесконечно:) Ключевые слова beth hierarchy, beth number, но, кому как, мне статья википедии ни о чем не сказала бы, а курс плавно подводит ко всему этому


                      1. NeoCode
                        26.03.2019 22:50
                        #19946886

                        Любопытно. Если бесконечностей бесконечно много, и есть итерационный процесс их порождения, то значит ли это что можно построить и исчисление бесконечностей? Определить над ними какие-то операции типа арифметических? Интересно что бы из этого получилось:)


                        1. Tzimie Автор
                          26.03.2019 22:57
                          #19946918
                          +2

                          И про это тоже есть порно это уже сделано
                          Через недельку напишу, надеюсь не засыпят работой


                          1. slonpts
                            27.03.2019 02:24
                            #19947472

                            Ждем с нетерпением!


                        1. 0xd34df00d
                          27.03.2019 00:43
                          #19947290

                          Получится арифметика кардиналов и ординалов (смотря сколько структуры вы насыпаете в ваши бесконечности). Она, кстати, забавная.


                    1. 0xd34df00d
                      27.03.2019 00:42
                      #19947286

                      Вот вся книжка про это.


        1. masai
          26.03.2019 20:48
          #19946430

          Например, по теореме Кантора мощность булеана (множества всех подмножеств) R больше мощности R. То есть, его мощность больше континуума.


          1. maxzhurkin
            26.03.2019 21:08
            #19946504

            А вы точно «больше» и «не меньше» не путаете?


            1. Tzimie Автор
              26.03.2019 21:27
              #19946556
              +1

              Мощность powerset всегда строго больше мощности исходного множества


              1. Druu
                27.03.2019 18:00
                #19951178

                Что, конечно, значит лишь то, что в рассматриваемой модели не находится подходящая биекция ;)


  1. lostmsu
    26.03.2019 18:12
    #19945710
    +1

    Статья интересная, но, честно говоря, её тяжелее читать, чем ту же Википедию на соответствующие темы. См., например, статью про Busy Beaver


    1. DouTro
      28.03.2019 16:14
      #19955558

      Согласен. Много сумбура, темы прыгают и центральная мысль не особо понятна. Вывода тоже никакого: я вам тут набросал мыслей, а вы уже думайте к чему.

      Со стилем бы надо хорошо поработать.


  1. ramyalexis
    27.03.2019 12:51
    #19949410
    +1

    Про стрелки: habr.com/ru/post/390399


    1. Tzimie Автор
      27.03.2019 12:53
      #19949424

      Если в каком-то явлении вы замечаете, что с какого-то момента начинают повторяться лишь ухудшающиеся (в лучшем случае, такие же) копии того, что уже было раньше — то это дурная бесконечность,


      Напомнило critical point of embedding… для недостижимых кардиналов.


    1. KvanTTT
      27.03.2019 13:54
      #19949810

      Вот более полная статья: О действительно БОЛЬШИХ числах (часть 1). К сожалению, автор так и не опубликовал вторую часть.


  1. Tzimie Автор
    27.03.2019 14:44
    #19950026

    Хорошая статья. Жаль что вторую часть он так и не написал.


    Однако мне fast growing hierarchy ближе, они и обгоняет все виды стрелок, и более строга, и замаплена на хорошо отработанную теорию ординалов


  1. celen
    27.03.2019 16:10
    #19950508

    Можете объяснить парадокс насчет FOOT?
    Допустим, FOOT(1000) — самое больше число, которое может описать математик, использовав не более 1000 символов на заданном языке. Если в этом языке есть возможность написать «Введем функцию FOOT(n), которая есть самое большое число, которое можно записать на этом языке», то, вполне очевидно, что можно оставшиеся символы потратить на запись FOOT(100000)+1, потратив на этом совсем немного символов. Таким образом, FOOT(1000) > FOOT(100000), что противоречит очевидной монотонности FOOT. Поэтому в этом языке нет такой возможности. Но в русском языке-то она есть!


    1. Arqwer
      27.03.2019 16:38
      #19950630

      Может быть дело в том, что русский язык не очень то формальная система, и поэтому не существует самого большого числа с описанием не длиннее n? Фраза "самое большое число, которое можно описать на русском языке за 100 букв, плюс один" на мой взгляд вообще не задаёт никакого числа, так как если бы оно задавало число, то она бы противоречила сама себе. Тут есть отсылка из фразы на свойства языка самой фразы. Наверное в любом формальном языке будет невозможно составить фразу "самое большое число с описанием не больше 100 букв на этом языке". Тут очень похоже на парадокс лжеца: "это утверждение ложно" — не может иметь ни статус "истина" ни статус "ложь", и выход в том что оно вообще не является утверждением, ровно по этой причине. Наверное также и с вашей фразой, только вместо невозможности присваивания фразе статуса истина/ложь тут невозможно присвоить фразе число.


      1. Tzimie Автор
        27.03.2019 16:41
        #19950652

        Формула в языке 1 порядка имеется в виду, а не произвольные слова


    1. vics001
      28.03.2019 00:06
      #19952614

      И в русском нет. «то, вполне очевидно, что можно оставшиеся символы потратить на запись FOOT(100000)+1» — не очевидно, вы не сможете в том же алфавите описать эту функцию и поэтому получили противоречие.


  1. dim2r
    27.03.2019 16:40
    #19950642

    одна из любимых статей на эту тему

    Георг Кантор и рождение теории трансфинитных множеств
    yadi.sk/i/DZgKURhK7aNWRA