Здравствуйте, друзья. Уже завтра стартует курс «Алгоритмы для разработчиков», а у нас остался один неопубликованный перевод. Собственно исправляемся и делимся с вами материалом. Поехали.
Быстрое преобразование Фурье (БПФ — англ. FFT) является одним из важнейших алгоритмов обработки сигналов и анализа данных. Я пользовался им годами, не имея формальных знаний в области компьютерных наук. Но на этой неделе мне пришло в голову, что я никогда не задавался вопросом, как БПФ так быстро вычисляет дискретное преобразование Фурье. Я стряхнул пыль со старой книги по алгоритмам, открыл ее, и с удовольствием прочитал об обманчиво простой вычислительной уловке, которую Дж. В. Кули и Джон Тьюки описали в своей классической работе 1965 года, посвященной этой теме.

Цель этого поста — окунуться в алгоритм БПФ Кули-Тьюки, объясняя симметрии, которые к нему приводят, и показать несколько простых реализаций на Python, применяющих теорию на практике. Я надеюсь, что это исследование даст специалистам по анализу данных, таким как я, более полную картину того, что происходит под капотом используемых нами алгоритмов.
Дискретное преобразование Фурье
БПФ — это быстрый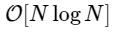 алгоритм для вычисления дискретного преобразования Фурье (ДПФ), которое напрямую вычисляется за
алгоритм для вычисления дискретного преобразования Фурье (ДПФ), которое напрямую вычисляется за 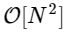 . ДПФ, как и более знакомая непрерывная версия преобразования Фурье, имеет прямую и обратную форму, которые определяются следующим образом:
. ДПФ, как и более знакомая непрерывная версия преобразования Фурье, имеет прямую и обратную форму, которые определяются следующим образом:
Прямое дискретное преобразование Фурье (ДПФ):
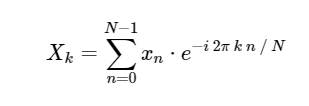
Обратное дискретное преобразование Фурье (ОДПФ):
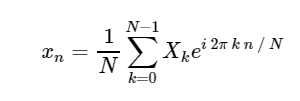
Преобразование из
Из-за важности БПФ (далее может быть использовано равносильное FFT — Fast Fourier Transform) во многих областях Python содержит множество стандартных инструментов и оболочек для его вычисления. И NumPy, и SciPy имеют оболочки из чрезвычайно хорошо протестированной библиотеки FFTPACK, которые находятся в подмодулях
На данный момент, однако, давайте оставим эти реализации в стороне и зададимся вопросом, как мы можем вычислить БПФ в Python с нуля.
Вычисление дискретного преобразования Фурье
Для простоты мы будем касаться только прямого преобразования, поскольку обратное преобразование может быть реализовано очень похожим образом. Взглянув на приведенное выше выражение ДПФ (DFT), мы видим, что это не более чем прямолинейная линейная операция: умножение матрицы на вектор
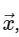
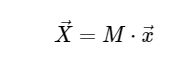
с матрицей М, заданной
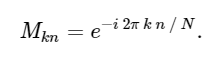
Имея это в виду, мы можем вычислить ДПФ с использованием простого умножения матрицы следующим образом:
In [1]:
Мы можем перепроверить результат, сравнив его со встроенной в numpy БПФ-функцией:
In [2]:
0ut[2]:
Просто чтобы подтвердить медлительность нашего алгоритма, мы можем сравнить время выполнения этих двух подходов:
In [3]:
Мы более чем в 1000 раз медленнее, что и следовало ожидать для такой упрощенной реализации. Но это не самое худшее. Для входного вектора длины N алгоритм БПФ масштабируется как , в то время как наш медленный алгоритм масштабируется как
, в то время как наш медленный алгоритм масштабируется как 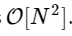 . Это означает, что для
. Это означает, что для 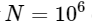 элементов мы ожидаем, что БПФ завершится за где-то около 50 мс, в то время как наш медленный алгоритм займет около 20 часов!
элементов мы ожидаем, что БПФ завершится за где-то около 50 мс, в то время как наш медленный алгоритм займет около 20 часов!
Так как же БПФ добивается такого ускорения? Ответ заключается в использовании симметрии.
Симметрии в дискретном преобразовании Фурье
Одним из наиболее важных инструментов в построении алгоритмов является использование симметрий задачи. Если вы можете аналитически показать, что одна часть проблемы просто связана с другой, вы можете вычислить подрезультат только один раз и сэкономить эти вычислительные затраты. Кули и Тьюки использовали именно этот подход при получении БПФ.
Мы начнем с вопроса о значении . Из нашего выражения выше:
. Из нашего выражения выше:

где мы использовали тождество exp [2? i n] = 1, которое выполняется для любого целого числа n.
Последняя строка хорошо показывает свойство симметрии ДПФ:
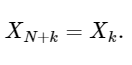
Простым расширением,
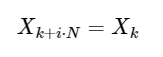
для любого целого числа i. Как мы увидим ниже, эту симметрию можно использовать для гораздо более быстрого вычисления ДПФ.
ДПФ в БПФ: использование симметрии
Кули и Тьюки показали, что можно разделить вычисления БПФ на две меньшие части. Из определения ДПФ имеем:
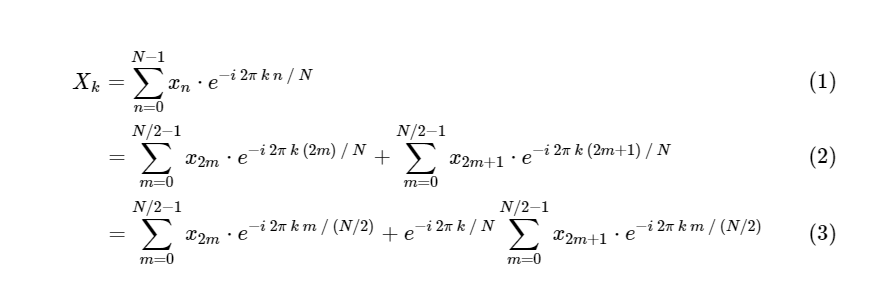
Мы разделили одно дискретное преобразование Фурье на два слагаемых, которые сами по себе очень похожи на меньшие дискретные преобразования Фурье, одно на значения с нечетным номером и одно на значения с четным номером. Однако до сих пор мы не сохранили никаких вычислительных циклов. Каждый член состоит из (N / 2) ? N вычислений, всего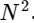 .
.
Хитрость заключается в использовании симметрии в каждом из этих условий. Поскольку диапазон k равен 0?k <N, а диапазон n равен 0?n <M?N / 2, мы видим из свойств симметрии выше, что нам нужно выполнить только половину вычислений для каждой подзадачи. Наше вычисление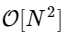 стало
стало 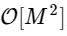 , где M в два раза меньше N.
, где M в два раза меньше N.
Но причин останавливаться на этом нет: пока наши меньшие преобразования Фурье имеют четное M, мы можем повторно применять этот подход «разделяй и властвуй», каждый раз вдвое уменьшая вычислительные затраты, пока наши массивы не станут достаточно маленькими, чтобы стратегия больше не сулила выгоды. В асимптотическом пределе этот рекурсивный подход масштабируется как O [NlogN].
Этот рекурсивный алгоритм может быть очень быстро реализован на Python, отталкиваясь от нашего медленного ДПФ кода, когда размер подзадачи становится достаточно маленьким:
In [4]:
Здесь мы сделаем быструю проверку того, что наш алгоритм дает правильный результат:
In [5]:
Out[5]:
Сопоставим этот алгоритм с нашей медленной версией:
-In [6]:
Наш расчет быстрее чем прямая версия на порядок! Более того, наш рекурсивный алгоритм асимптотически : мы реализовали быстрое преобразование Фурье.
: мы реализовали быстрое преобразование Фурье.
Обратите внимание, что мы все еще не приблизились к скорости встроенного алгоритма FFT в numpy, и этого следовало ожидать. Алгоритм FFTPACK, стоящий за
Хорошая стратегия для ускорения кода при работе с Python / NumPy — по возможности векторизовать повторяющиеся вычисления. Это мы можем сделать — в процессе удалять наши рекурсивные вызовы функций, что сделает наш Python FFT еще более эффективным.
Векторизованная Numpy-версия
Обратите внимание, что в вышеупомянутой рекурсивной реализации FFT на самом низком уровне рекурсии мы выполняем N / 32 идентичных матрично-векторных произведений. Эффективность нашего алгоритма выиграет, если одновременно вычислить эти матрично-векторные произведения как единое матрично-матричное произведение. На каждом последующем уровне рекурсии мы также выполняем повторяющиеся операции, которые можно векторизовать. NumPy отлично справляется с такой операцией, и мы можем использовать этот факт для создания этой векторизованной версии быстрого преобразования Фурье:
In [7]:
Хотя алгоритм немного более непрозрачен, это просто перестановка операций, используемых в рекурсивной версии, с одним исключением: мы используем симметрию в вычислении коэффициентов и строим только половину массива. Опять же, мы подтверждаем, что наша функция дает правильный результат:
In [8]:
Out[8]:
Поскольку наши алгоритмы становятся намного более эффективными, мы можем использовать больший массив для сравнения времени, оставляя
In [9]:
Мы улучшили нашу реализацию еще на порядок! Сейчас мы находимся на расстоянии примерно в 10 раз от эталона FFTPACK, используя всего пару десятков строк чистого Python + NumPy. Хотя это все еще не соответствует в вычислительном отношении, с точки зрения читаемости версия Python намного превосходит исходный код FFTPACK, который вы можете просмотреть здесь.
Итак, как FFTPACK достигает этого последнего ускорения? Ну, в основном, это просто вопрос детальной бухгалтерии. FFTPACK тратит много времени на повторное использование любых промежуточных вычислений, которые можно использовать повторно. Наша клочковатая версия все еще включает в себя избыток выделения памяти и копирования; на низкоуровневом языке, таком как Fortran, легче контролировать и минимизировать использование памяти. Кроме того, алгоритм Кули-Тьюки можно расширить, чтобы использовать разбиения размером, отличным от 2 (то, что мы здесь реализовали, известно как БПФ Кули-Тьюки радикса по основе 2). Также могут быть использованы другие более сложные алгоритмы БПФ, в том числе принципиально отличные подходы, основанные на сверточных данных (см., Например, алгоритм Блюштейна и алгоритм Рейдера). Комбинация вышеупомянутых расширений и методов может привести к очень быстрым БПФ даже на массивах, размер которых не является степенью двойки.
Хотя функции на чистом Python, вероятно, бесполезны на практике, я надеюсь, что они преподнесли некоторую интуицию в том, что происходит на фоне анализа данных на основе FFT. Как специалисты по данным, мы можем справиться с реализацией «черного ящика» фундаментальных инструментов, созданных нашими более алгоритмически настроенными коллегами, но я твердо убежден, что чем больше у нас понимания о алгоритмах низкого уровня, которые мы применяем к нашим данным, тем лучшими практиками мы будем.
Этот пост был полностью написан в блокноте IPython. Полный блокнот можно скачать здесь или посмотреть статически здесь.
Многие могут заметить, что материал далеко не новый, но, как нам кажется, вполне актуальный. В общем пишите была ли статья полезной. Ждём ваши комментарии.
Быстрое преобразование Фурье (БПФ — англ. FFT) является одним из важнейших алгоритмов обработки сигналов и анализа данных. Я пользовался им годами, не имея формальных знаний в области компьютерных наук. Но на этой неделе мне пришло в голову, что я никогда не задавался вопросом, как БПФ так быстро вычисляет дискретное преобразование Фурье. Я стряхнул пыль со старой книги по алгоритмам, открыл ее, и с удовольствием прочитал об обманчиво простой вычислительной уловке, которую Дж. В. Кули и Джон Тьюки описали в своей классической работе 1965 года, посвященной этой теме.

Цель этого поста — окунуться в алгоритм БПФ Кули-Тьюки, объясняя симметрии, которые к нему приводят, и показать несколько простых реализаций на Python, применяющих теорию на практике. Я надеюсь, что это исследование даст специалистам по анализу данных, таким как я, более полную картину того, что происходит под капотом используемых нами алгоритмов.
Дискретное преобразование Фурье
БПФ — это быстрый
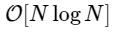 алгоритм для вычисления дискретного преобразования Фурье (ДПФ), которое напрямую вычисляется за
алгоритм для вычисления дискретного преобразования Фурье (ДПФ), которое напрямую вычисляется за 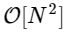 . ДПФ, как и более знакомая непрерывная версия преобразования Фурье, имеет прямую и обратную форму, которые определяются следующим образом:
. ДПФ, как и более знакомая непрерывная версия преобразования Фурье, имеет прямую и обратную форму, которые определяются следующим образом:Прямое дискретное преобразование Фурье (ДПФ):
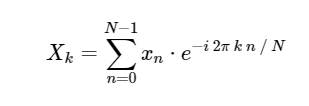
Обратное дискретное преобразование Фурье (ОДПФ):
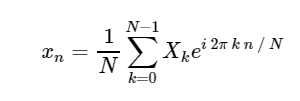
Преобразование из
xn > Xk является переводом из конфигурационного пространства в пространство частотное и может быть очень полезным как для исследования спектра мощности сигнала, так и для преобразования определенных задач для более эффективного вычисления. Некоторые примеры этого в действии вы можете найти в главе 10 нашей будущей книги по астрономии и статистике, где также можно найти изображения и исходный код на Python. Пример использования БПФ для упрощения интеграции сложных в противном случае дифференциальных уравнений смотрите в моем посте «Решение уравнения Шредингера в Python».Из-за важности БПФ (далее может быть использовано равносильное FFT — Fast Fourier Transform) во многих областях Python содержит множество стандартных инструментов и оболочек для его вычисления. И NumPy, и SciPy имеют оболочки из чрезвычайно хорошо протестированной библиотеки FFTPACK, которые находятся в подмодулях
numpy.fft и scipy.fftpack соответственно. Самый быстрый БПФ, о котором я знаю, находится в пакете FFTW, который также доступен в Python через пакет PyFFTW.На данный момент, однако, давайте оставим эти реализации в стороне и зададимся вопросом, как мы можем вычислить БПФ в Python с нуля.
Вычисление дискретного преобразования Фурье
Для простоты мы будем касаться только прямого преобразования, поскольку обратное преобразование может быть реализовано очень похожим образом. Взглянув на приведенное выше выражение ДПФ (DFT), мы видим, что это не более чем прямолинейная линейная операция: умножение матрицы на вектор
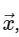
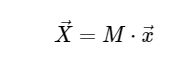
с матрицей М, заданной
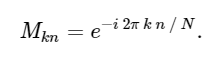
Имея это в виду, мы можем вычислить ДПФ с использованием простого умножения матрицы следующим образом:
In [1]:
import numpy as np
def DFT_slow(x):
"""Compute the discrete Fourier Transform of the 1D array x"""
x = np.asarray(x, dtype=float)
N = x.shape[0]
n = np.arange(N)
k = n.reshape((N, 1))
M = np.exp(-2j * np.pi * k * n / N)
return np.dot(M, x)Мы можем перепроверить результат, сравнив его со встроенной в numpy БПФ-функцией:
In [2]:
x = np.random.random(1024)
np.allclose(DFT_slow(x), np.fft.fft(x))0ut[2]:
TrueПросто чтобы подтвердить медлительность нашего алгоритма, мы можем сравнить время выполнения этих двух подходов:
In [3]:
%timeit DFT_slow(x)
%timeit np.fft.fft(x)10 loops, best of 3: 75.4 ms per loop
10000 loops, best of 3: 25.5 µs per loopМы более чем в 1000 раз медленнее, что и следовало ожидать для такой упрощенной реализации. Но это не самое худшее. Для входного вектора длины N алгоритм БПФ масштабируется как
 , в то время как наш медленный алгоритм масштабируется как
, в то время как наш медленный алгоритм масштабируется как 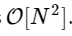 . Это означает, что для
. Это означает, что для 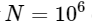 элементов мы ожидаем, что БПФ завершится за где-то около 50 мс, в то время как наш медленный алгоритм займет около 20 часов!
элементов мы ожидаем, что БПФ завершится за где-то около 50 мс, в то время как наш медленный алгоритм займет около 20 часов!Так как же БПФ добивается такого ускорения? Ответ заключается в использовании симметрии.
Симметрии в дискретном преобразовании Фурье
Одним из наиболее важных инструментов в построении алгоритмов является использование симметрий задачи. Если вы можете аналитически показать, что одна часть проблемы просто связана с другой, вы можете вычислить подрезультат только один раз и сэкономить эти вычислительные затраты. Кули и Тьюки использовали именно этот подход при получении БПФ.
Мы начнем с вопроса о значении
 . Из нашего выражения выше:
. Из нашего выражения выше:
где мы использовали тождество exp [2? i n] = 1, которое выполняется для любого целого числа n.
Последняя строка хорошо показывает свойство симметрии ДПФ:
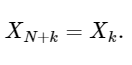
Простым расширением,
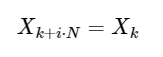
для любого целого числа i. Как мы увидим ниже, эту симметрию можно использовать для гораздо более быстрого вычисления ДПФ.
ДПФ в БПФ: использование симметрии
Кули и Тьюки показали, что можно разделить вычисления БПФ на две меньшие части. Из определения ДПФ имеем:
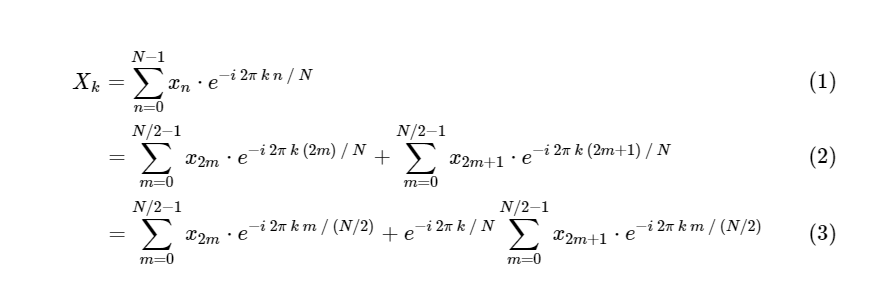
Мы разделили одно дискретное преобразование Фурье на два слагаемых, которые сами по себе очень похожи на меньшие дискретные преобразования Фурье, одно на значения с нечетным номером и одно на значения с четным номером. Однако до сих пор мы не сохранили никаких вычислительных циклов. Каждый член состоит из (N / 2) ? N вычислений, всего
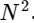 .
.Хитрость заключается в использовании симметрии в каждом из этих условий. Поскольку диапазон k равен 0?k <N, а диапазон n равен 0?n <M?N / 2, мы видим из свойств симметрии выше, что нам нужно выполнить только половину вычислений для каждой подзадачи. Наше вычисление
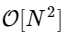 стало
стало 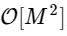 , где M в два раза меньше N.
, где M в два раза меньше N.Но причин останавливаться на этом нет: пока наши меньшие преобразования Фурье имеют четное M, мы можем повторно применять этот подход «разделяй и властвуй», каждый раз вдвое уменьшая вычислительные затраты, пока наши массивы не станут достаточно маленькими, чтобы стратегия больше не сулила выгоды. В асимптотическом пределе этот рекурсивный подход масштабируется как O [NlogN].
Этот рекурсивный алгоритм может быть очень быстро реализован на Python, отталкиваясь от нашего медленного ДПФ кода, когда размер подзадачи становится достаточно маленьким:
In [4]:
def FFT(x):
"""A recursive implementation of the 1D Cooley-Tukey FFT"""
x = np.asarray(x, dtype=float)
N = x.shape[0]
if N % 2 > 0:
raise ValueError("size of x must be a power of 2")
elif N <= 32: # this cutoff should be optimized
return DFT_slow(x)
else:
X_even = FFT(x[::2])
X_odd = FFT(x[1::2])
factor = np.exp(-2j * np.pi * np.arange(N) / N)
return np.concatenate([X_even + factor[:N / 2] * X_odd,
X_even + factor[N / 2:] * X_odd])Здесь мы сделаем быструю проверку того, что наш алгоритм дает правильный результат:
In [5]:
x = np.random.random(1024)
np.allclose(FFT(x), np.fft.fft(x))Out[5]:
TrueСопоставим этот алгоритм с нашей медленной версией:
-In [6]:
%timeit DFT_slow(x)
%timeit FFT(x)
%timeit np.fft.fft(x)10 loops, best of 3: 77.6 ms per loop
100 loops, best of 3: 4.07 ms per loop
10000 loops, best of 3: 24.7 µs per loopНаш расчет быстрее чем прямая версия на порядок! Более того, наш рекурсивный алгоритм асимптотически
 : мы реализовали быстрое преобразование Фурье.
: мы реализовали быстрое преобразование Фурье.Обратите внимание, что мы все еще не приблизились к скорости встроенного алгоритма FFT в numpy, и этого следовало ожидать. Алгоритм FFTPACK, стоящий за
fft numpy, — это реализация на Фортране, которая получила годы доработок и оптимизаций. Кроме того, наше решение NumPy включает в себя как рекурсию стека Python, так и выделение множества временных массивов, что увеличивает время вычислений.Хорошая стратегия для ускорения кода при работе с Python / NumPy — по возможности векторизовать повторяющиеся вычисления. Это мы можем сделать — в процессе удалять наши рекурсивные вызовы функций, что сделает наш Python FFT еще более эффективным.
Векторизованная Numpy-версия
Обратите внимание, что в вышеупомянутой рекурсивной реализации FFT на самом низком уровне рекурсии мы выполняем N / 32 идентичных матрично-векторных произведений. Эффективность нашего алгоритма выиграет, если одновременно вычислить эти матрично-векторные произведения как единое матрично-матричное произведение. На каждом последующем уровне рекурсии мы также выполняем повторяющиеся операции, которые можно векторизовать. NumPy отлично справляется с такой операцией, и мы можем использовать этот факт для создания этой векторизованной версии быстрого преобразования Фурье:
In [7]:
def FFT_vectorized(x):
"""A vectorized, non-recursive version of the Cooley-Tukey FFT"""
x = np.asarray(x, dtype=float)
N = x.shape[0]
if np.log2(N) % 1 > 0:
raise ValueError("size of x must be a power of 2")
# N_min here is equivalent to the stopping condition above,
# and should be a power of 2
N_min = min(N, 32)
# Perform an O[N^2] DFT on all length-N_min sub-problems at once
n = np.arange(N_min)
k = n[:, None]
M = np.exp(-2j * np.pi * n * k / N_min)
X = np.dot(M, x.reshape((N_min, -1)))
# build-up each level of the recursive calculation all at once
while X.shape[0] < N:
X_even = X[:, :X.shape[1] / 2]
X_odd = X[:, X.shape[1] / 2:]
factor = np.exp(-1j * np.pi * np.arange(X.shape[0])
/ X.shape[0])[:, None]
X = np.vstack([X_even + factor * X_odd,
X_even - factor * X_odd])
return X.ravel()Хотя алгоритм немного более непрозрачен, это просто перестановка операций, используемых в рекурсивной версии, с одним исключением: мы используем симметрию в вычислении коэффициентов и строим только половину массива. Опять же, мы подтверждаем, что наша функция дает правильный результат:
In [8]:
x = np.random.random(1024)
np.allclose(FFT_vectorized(x), np.fft.fft(x))Out[8]:
TrueПоскольку наши алгоритмы становятся намного более эффективными, мы можем использовать больший массив для сравнения времени, оставляя
DFT_slow:In [9]:
x = np.random.random(1024 * 16)
%timeit FFT(x)
%timeit FFT_vectorized(x)
%timeit np.fft.fft(x)10 loops, best of 3: 72.8 ms per loop
100 loops, best of 3: 4.11 ms per loop
1000 loops, best of 3: 505 µs per loopМы улучшили нашу реализацию еще на порядок! Сейчас мы находимся на расстоянии примерно в 10 раз от эталона FFTPACK, используя всего пару десятков строк чистого Python + NumPy. Хотя это все еще не соответствует в вычислительном отношении, с точки зрения читаемости версия Python намного превосходит исходный код FFTPACK, который вы можете просмотреть здесь.
Итак, как FFTPACK достигает этого последнего ускорения? Ну, в основном, это просто вопрос детальной бухгалтерии. FFTPACK тратит много времени на повторное использование любых промежуточных вычислений, которые можно использовать повторно. Наша клочковатая версия все еще включает в себя избыток выделения памяти и копирования; на низкоуровневом языке, таком как Fortran, легче контролировать и минимизировать использование памяти. Кроме того, алгоритм Кули-Тьюки можно расширить, чтобы использовать разбиения размером, отличным от 2 (то, что мы здесь реализовали, известно как БПФ Кули-Тьюки радикса по основе 2). Также могут быть использованы другие более сложные алгоритмы БПФ, в том числе принципиально отличные подходы, основанные на сверточных данных (см., Например, алгоритм Блюштейна и алгоритм Рейдера). Комбинация вышеупомянутых расширений и методов может привести к очень быстрым БПФ даже на массивах, размер которых не является степенью двойки.
Хотя функции на чистом Python, вероятно, бесполезны на практике, я надеюсь, что они преподнесли некоторую интуицию в том, что происходит на фоне анализа данных на основе FFT. Как специалисты по данным, мы можем справиться с реализацией «черного ящика» фундаментальных инструментов, созданных нашими более алгоритмически настроенными коллегами, но я твердо убежден, что чем больше у нас понимания о алгоритмах низкого уровня, которые мы применяем к нашим данным, тем лучшими практиками мы будем.
Этот пост был полностью написан в блокноте IPython. Полный блокнот можно скачать здесь или посмотреть статически здесь.
Многие могут заметить, что материал далеко не новый, но, как нам кажется, вполне актуальный. В общем пишите была ли статья полезной. Ждём ваши комментарии.
Комментарии (4)

Refridgerator
30.04.2019 06:07Единственный способ по-настоящему понять, как работает БПФ — это написать его самому, ну или хотя портировать с одного языка программирования на другой. Чтобы своими глазами в режиме отладки увидеть, как в массиве крутятся и складываются векторы. И про bit-reversal permutation тоже ничего не сказано, и про (а)симметричное масштабирование, и про симметрию (комплексного) спектра на действительных входных данных…

Refridgerator
30.04.2019 06:29Преобразование из xn > Xk является переводом из конфигурационного пространства в пространство частотное
По русски это должно звучать как «переходом из временной области в частотную и наоборот». Иногда вместо «область» говорят «домен» (калька с английского).

noonv
30.04.2019 11:26Python 3.6 ругается:
Slice indices must be integers or None or have __index__ method
на строчку:
return np.concatenate([X_even + factor[:N / 2] * X_odd, X_even + factor[N / 2:] * X_odd])
хочет, чтобы индексы обернули в int()


ZEvS_Poisk
Когда меня просят «на пальцах» рассказать про БПФ и ДПФ, особенно часто об этом просят люди, которые «понимают в технике», то обычно я начинаю рассказывать примерно так: Фурье — это тот же самый радиоприемник, только математический. В обычном приемнике входной сигнал умножается (смесителем) на гетеродин. Гетеродин — это синусоидальный сигнал выработанный локально (в приемнике), если после такого умножения выделить постоянную составляющую, то она будет пропорциональна амплитуде сигнала на частоте гетеродина.
На самом деле все немного сложнее, гетеродин должен быть двойной (синусоида и косинусоида), если умножить анализируемый сигнал на синусоиду и косинусоиду, а потом усреднить все полученные значения, то мы получим вектор, где длинна вектора есть амплитуда, а арктангенс составляющих есть разность фаз, между сигналом и гетеродином.
Так вот если постоянно менять частоту гетеродина, то мы просканируем все частоты и получим спектр. Так работают (работали) аналоговые спектроанализаторы.
ДПФ делает то-же самое, абсолютно. Только не в реальном времени и не с живым сигналом, а с готовым — оцифрованным массивом данных.
БПФ модифицированный и оптимизированный алгоритм, который работает быстрее засчет уменьшения количества умножений. В ДПФ каждая выборка сигнала умножается на синус и косинус «гетеродина», но выборки синусов и косинусов разных частот совпадают во времени, и чтобы не использовати их повторно, они используются оптимально, засчет сортировок и перестановок.
Ну, а дальше уже формулы.
Статья отличная, прочитал с огромным удовольствием, автору спасибо!