Добро пожаловать на одну из лекций курса CS231n: Convolutional Neural Networks for Visual Recognition.

Содержание
- Обзор архитектуры
- Слои в свёрточной нейронной сети
— Свёрточный слой
— Слой подвыборки
— Слой нормализации
— Полносвязный слой
— Преобразование полносвязных слоёв в свёрточные слои - Архитектура свёрточных нейронных сетей
— Шаблоны слоёв
— Шаблоны размеров слоёв
— Изучение кейсов (LeNet, AlexNet, ZFNet, GoogLeNet, VGGNet)
— Вычислительные аспекты - Дополнительная литература
Свёрточные нейронные сети (CNN / ConvNets)
Свёрточные нейронные сети очень похожи на обычные нейронные сети, которые мы изучали в прошлой главе (отсылка к прошлой главе курса CS231n): они состоят из нейронов, которые, в свою очередь, содержат изменяемые веса и смещения. Каждый нейрон получает какие-то входные данные, вычисляет скалярное произведение и, опционально, использует нелинейную функцию активации. Вся сеть по-прежнему представляет собой единственную дифференциируемую функцию оценки: из исходного набора пикселей (изображения) на одном конце до распределения вероятностей принадлежности к определённому классу на другом конце. У этих сетей по-прежнему есть функция потерь (например, SVM/Softmax) на последнем (полносвязном) слое и все те советы и рекомендации, которые были даны в предыдущей главе относящейся к обычным нейронным сетям, актуальны и для свёрточных нейронных сетей.
Так что же изменилось? Архитектура свёрточных нейронных сетей явно предполагает получение на входе изображений, что позволяет нам учесть определённые свойства входных данных в самой архитектуре сети. Эти свойства позволяют реализовать функцию прямого распространения эффективнее и сильно уменьшают общее количество параметров в сети.
Обзор архитектуры
Вспоминаем обычные нейронные сети. Как мы уже видели в предыдущей главе, нейронные сети получают входные данные (единственный вектор) и преобразовывают его "проталкивая" через серию скрытых слоёв. Каждый скрытый слой состоит из определённого количества нейронов, каждый из которых связан со всеми нейронами предыдущего слоя и где нейроны на каждом слое полностью независимы от других нейронов на этом же уровне. Последний полносвязный слой называется "выходным слоем" и в задачах классификации представляет собой распределение оценок по классам.
Обычные нейронные сети плохо масштабируются для бОльших изображений. В наборе данных CIFAR-10, изображения размером 32х32х3 (32 пикселя высота, 32 пикселя ширина, 3 цветовых канала). Для обработки такого изображения полносвязный нейрон в первом скрытом слое обычной нейронной сети будет иметь 32х32х3 = 3072 весов. Такое количество всё ещё является допустимым, но становится очевидным тот факт, что подобная структура не будет работать с изображениями бОльшего размера. Например, изображение большего размера — 200х200х3, приведёт к тому, что количество весов станет равным 200х200х3 = 120 000. Более того, нам понадобится не один подобный нейрон, поэтому общее количество весов быстро начнёт расти. Становится очевидным тот факт, что полносвязность чрезмерна и большое количество параметров быстро приведут сеть к переобученности.
3D-представления нейронов. Свёрточные нейронные сети используют тот факт, что входные данные — изображения, поэтому они образуют более чувствительную архитектуру к подобному типу данных. В частности, в отличие от обычных нейронных сетей, слои в свёрточной нейронной сети располагают нейроны в 3 измерениях — ширине, высоте, глубине (Заметка: слово "глубина" относится к 3-му измерению активационных нейронов, а не глубине самой нейронной сети измеряемой в количестве слоёв). Например, входные изображения из набора данных CIFAR-10 являются входными данными в 3D-представлении, размерность которых равна 32х32х3 (ширина, высота, глубина). Как мы увидим позднее, нейроны в одном слое будут связаны с небольшим количеством нейронов в предыдущем слое, вместо того чтобы быть связанными со всеми предыдущими нейронами слоя. Более того, выходной слой для изображения из набора данных CIFAR-10 будет иметь размерность 1х1х10, потому что подбираясь к концу нейронной сети мы уменьшим размер изображения до вектора оценок по классам, расположенного вдоль глубины (3-го измерения).
Визуализация:
| Стандартная нейронная сеть | Свёрточная нейронная сеть |
|---|---|
 |
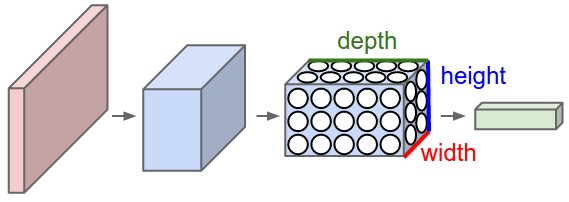 |
С левой стороны: стандартная 3-х слойная нейронная сеть.
С правой стороны: свёрточная нейронная сеть располагает свои нейроны в 3-х измерениях (ширине, высоте, глубине), как это показано на одном из слоёв. Каждый слой свёрточной нейронной сети преобразует 3D-представление входных данных в 3D-представление выходных данных в виде нейронов активации. В этом примере красный входной слой содержит изображение, поэтому его размеры будут равны размерам изображения, а глубина будет равна 3 (три канала — red, green, blue).
Свёрточная нейронная сеть состоит из слоёв. Каждый слой представляет собой простой API: преобразует входное 3D-представление в выходное 3D-представление некой дифференциируемой функцией, которая может содержать, а может и не содержать параметров.
Слои, используемые для построения свёрточных нейронных сетей
Как мы уже описали выше, простая свёрточная нейронная сеть это набор слоёв, где каждый слой преобразует одно представление в другое с использованием некой дифференциируемой функцией. Мы используем три главных типа слоёв для построения свёрточных нейронных сетей: свёрточный слой, слой подвыборки и полносвязный слой (такой же, какой мы используем в обычной нейронной сети). Располагаем эти слои последовательно для получения архитектуры СНС.
Пример архитектуры: обзор. Чуть ниже мы погрузимся в детали, а пока для набора данных CIFAR-10 архитектура нашей свёрточной нейронной сети может быть такой [INPUT -> CONV -> RELU -> POOL -> FC]. Теперь подробнее:
INPUT[32x32x3] будет содержать исходные значения пикселей изображения, в нашем случае изображение размерами 32px в ширину, 32px в высоту и 3 цветовыми каналами R, G, B.CONV-слой произведёт набор выходных нейронов, которые будут связаны с локальной областью входного исходного изображения; каждый такой нейрон будет вычислять скалярное произведение между своими весами и той небольшой частью исходного изображения с которым он связан. Выходным значением может быть 3D-представление размером32х32х12, если, например, мы решим использовать 12 фильтров.RELU-слой будет применять по-элементно функцию активацииmax(0, x). Это преобразование не изменит размерности данных —[32x32x12].POOL-слой произведёт операцию сэмплирования изображения по двум измерениям — высоте и ширине, что в результате даст нам новое 3D-представление[16х16х12].FC-слой (полносвязный слой) подсчитает оценки по классам, результатирующая размерность будет равна[1x1x10], где каждое из 10 значений будет соответствовать оценке определенного класса среди 10 категорий изображений из CIFAR-10. Как и в обычных нейронных сетях, каждый нейрон этого слоя будет связан со всеми нейронами предыдущего слоя (3D-представления).
Именно таким образом свёрточная нейронная сеть преобразует исходное изображение, слой за слоем, от начального значения пикселя до итоговой оценки класса. Обратите внимание, что некоторые слои содержат параметры, а некоторые — нет. В частности, CONV/FC-слои осуществляют трансформацию, которая является не только функцией зависящей от входных данных, но и зависящей от внутренних значений весов и смещений в самих нейронах. С другой стороны, RELU/POOL-слои применяют непараметризованные функции. Параметры в CONV/FC-слоях будут натренированы градиентным спуском таким образом, чтобы входные данные получали соответствующие корректные выходные метки.
Подведём итоги:
- Архитектура свёрточной нейронной сети, в своём простейшем представлении, представляет собой упорядоченный набор слоёв преобразующий представление изображения в другое представление, например, оценки принадлежности к классам.
- Существует несколько различных типов слоёв (CONV — свёрточный слой, FC — полносвязный, RELU — функция активации, POOL — слой подвыборки — наиболее популярные).
- Каждый слой на вход получает 3D-представление, преобразует его в выходное 3D-представление используя дифференциируемую функцию.
- Каждый слой может иметь и не иметь параметров (CONV/FC — имеют параметры, RELU/POOL — нет).
- Каждый слой может иметь и не иметь гипер-параметров (CONV/FC/POOL — имеют, RELU — нет)
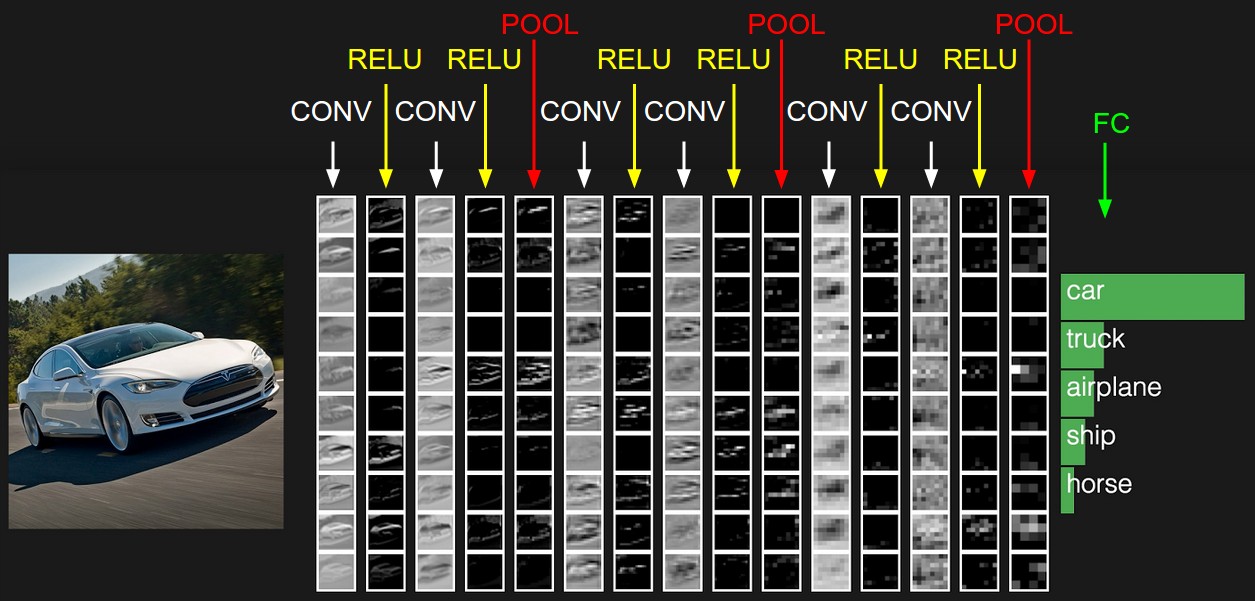
Исходное представление содержит значения пикселей изображения (слева) и оценки по классам к которым относится объект на изображении (справа). Каждая трансформация представления отмечена в виде столбца.
Свёрточный слой
Свёрточный слой является основным слоем при построении свёрточных нейронных сетей.
Обзор без погружения в особенности работы головного мозга. Давайте сперва попробуем разобраться в том, что же всё-таки вычисляет CONV-слой без погружения и затрагивания темы мозга и нейронов. Параметры свёрточного слоя состоят из набора обучаемых фильтров. Каждый фильтр представляет собой небольшую сетку вдоль ширины и высоты, но простирающуюся по всей глубине входного представления.
Например, стандартный фильтр на первом слое свёрточной нейронной сети может иметь размеры 5х5х3 (5px — ширина и высота, 3 — количество цветовых каналов). Во время прямого прохода мы перемещаем (если быть точными — свёртываем) фильтр вдоль ширины и высоты входного представления и вычисляем скалярное произведение между значениями фильтра и подлежащими значениями входного представления в любой точке. В процессе перемещения фильтра вдоль ширины и высоты входного представления мы формируем 2х мерную карту активации, которая содержит значения применения данного фильтра к каждой из областей входного представления. Интуитивно становится ясно, что сеть обучит фильтры активироваться при виде определённого визуального признака, например, прямой под определённым углом или колесообразных представлений на более высоких уровнях. Теперь, когда мы применили все наши фильтры к исходному изображению, например, их было 12. В результате применения 12 фильтров мы получили 12 активационных карт размерностью 2. Чтобы произвести выходное представление — объединим эти карты (последовательно по 3-му измерению) и получим представление размерностью [WxHx12].
Обзор к которому мы подключим мозг и нейроны. Если вы фанат мозга и нейронов, то можете себе представить, что каждый нейрон "смотрит" на большой участок входного представления и передаёт информации об этом участке соседствующими с ним нейронам. Чуть ниже мы обсудим детали связности нейронов, их расположения в пространстве и механизм совместного использования параметров.
Локальная связность. Когда мы имеем дело с входными данными с большим количеством измерений, например, как в случае с изображениями, то, как мы уже видели, нет абсолютно никакой необходимости связывать нейроны со всеми нейронами на предыдущем слое. Вместо этого мы будем соединять нейроны только с локальными областями входного представления. Пространственная степень связности является одним из гипер-параметров и называется receptive field (рецептивное поле нейрона — размер того самого фильтра / ядра свёртки). Степень связности вдоль 3-го измерения (глубины) всегда равна глубине исходного представления. Очень важно вновь акцентировать на этом внимание, внимание на том, как мы определяем пространственные измерения (ширину и высоту) и глубину: связи нейрона локальны по ширине и высоте, но всегда простираются по всей глубине входного представления.
Пример 1. Представим, что входное представление имеет размер 32х32х3 (RGB, CIFAR-10). Если размер фильтра (рецептивное поле нейрона) будет размером 5х5, тогда каждый нейрон в свёрточном слое будет иметь веса к области размером 5х5х3 исходного представления, что в итоге приведёт к установлению 5х5х3 = 75 связей (весов) + 1 параметр смещения. Обратите внимание, что степень связности по глубине должна быть равна 3, так как это размерность исходного представления.
Пример 2. Представим, что входное представление имеет размер 16х16х20. Используя в качестве примера рецептивное поле нейрона размером 3х3, каждый нейрон свёрточного слоя будет иметь 3х3х20 = 180 связей (весов) + 1 параметр смещения. Обратите внимание, что связность локальна по ширине и высоте, но полная в глубину (20).
| #1 | #2 |
|---|---|
 |
 |
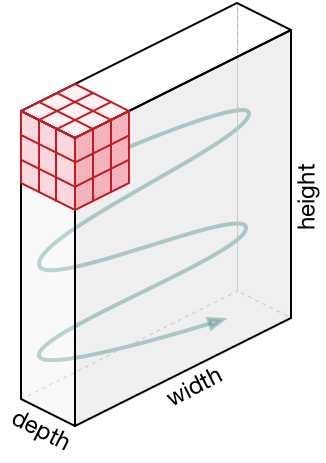
C левой стороны: входное представление отображено красным цветом (например, изображение размером 32х32х3 CIFAR-10) и пример представления нейронов в первом свёрточном слое. Каждый нейрон в свёрточном слое связан только с локальной областью входного представления, но полностью по глубине (в примере — по всем цветовым каналам). Обратите внимание, что на изображении множество нейронов (в примере — 5) и расположены они по 3-му измерению (глубине) — чуть ниже будут даны пояснения относительно такого расположения.
С правой стороны: нейроны из нейронной сети по-прежнему остаются неизменными: они по-прежнему вычисляют скалярное произведение между своими весами и входными данными, применяют функцию активации, но их связность теперь ограничена пространственной локальной областью.
Пространственное расположение. Мы уже разобрались со связностью каждого нейрона в свёрточном слое с входным представлением, но ещё не обсудили сколько этих нейронов или как они располагаются. Три гипер-параметра влияют на размер выходного представления: глубина, шаг и выравнивание.
- Глубина выходного представления является гипер-параметром: соответствует количество фильтров, которые мы хотим применить, каждый из которых обучается чему-то другому в исходном представлении. Например, если первый свёрточный слой принимает на вход изображение, тогда разные нейроны вдоль 3-го измерения (глубины) могут активироваться при присутствии различных ориентаций прямых в определённой области или скоплений определенного цвета. Набор нейронов, которые "смотрят" на одну и ту же область входного представления, мы будем называть глубинным столбцом (или "фиброй" — волокном).
- Мы должны определить шаг (размер смещения в пикселях) с которым будет перемещаться фильтр. Если шаг равен 1, то мы смещаем фильтр на 1 пиксель за одну итерацию. Если шаг равен 2 (или, что ещё реже используется — 3 и более), то смещение происходит на каждые два пикселя за одну итерацию. Больший шаг приводит к меньшему размеру выходного представления.
- Как мы вскоре увидим, иногда необходимо будет дополнять входное представление по краям нулями. Размер выравнивания (количество нулевых дополняемых столбцов / строк) так же является гипер-параметром. Приятной особенностью использования выравнивания является тот факт, что выравнивание позволит нам контролировать размерность выходного представления (чаще всего мы будем сохранять исходные размеры представления — сохранение ширины и высоты входного представления с шириной и высотой выходного представления).
Мы можем вычислить итоговую размерность выходного представления представив её функцией от размеров входного представления (W), размером рецептивного поля нейронов свёрточного слоя (F), шагом (S) и размером выравнивания (P) на границах. Вы можете убедиться сами, что корректная формула для подсчёта количества нейронов в выходном представлении выглядит следующим образом (W — F + 2P) / S + 1. Например, для входного представления размером 7х7 и размером фильтра 3х3, шагом 1 и выравниванием 0, мы получим выходное представление размером 5х5. С шагом 2 мы бы получили выходное представление размером 3х3. Давайте рассмотрим ещё один пример, на этот раз проиллюстрированный графически:

Иллюстрация пространственного расположения. В этом примере только одно пространственное измерение (x-ось), один нейрон с рецептивным полем F=3, размер входного представления W=5 и выравниванием P = 1. С левой стороны: рецептивное поле нейрона перемещается с шагом S = 1, что в результате даёт размер выходного представления (5 — 3 + 2) / 1 + 1 = 5. С правой стороны: нейрон использует рецептивное поле размером S = 2, что в результате даёт размер выходного представления (5 — 3 + 2) / 2 + 1 = 3. Обратите внимание, что размер шага S = 3 не может быть использован, так как при таком размере шага рецептивное поле не захватит часть изображения. Если использовать нашу формулу, то (5 — 3 + 2) = 4 не кратно 3. Веса нейронов в этом примере равны [1, 0, -1] (как показано на самой правой картинке), а смещение равно нулю. Эти веса совместно используются всеми жёлтыми нейронами.
Использование выравнивания. Обратите внимание на пример с левой стороны, который содержит 5 элементов на выходе и 5 элементов на выходе. Это сработало потому, что размер рецептивного поля (фильтра) был равен 3 и мы воспользовались выравниванием P = 1. Если бы не было выравнивания, то размер выходного представления был бы равен 3, потому что именно столько нейронов туда "поместилось" бы. В общем, установление размера выравнивания P = (F — 1) / 2 при шаге равном S = 1 позволяет получить размер выходного представления аналогичный входному представлению. Подобный подход с использованием выравнивания часто применяется на практике, а причины мы обсудить чуть ниже, когда будем говорить об архитектуре свёрточных нейронных сетей.
Ограничения на размер шага. Обратите внимание, что гипер-параметры отвечающие за пространственное расположение, так же связаны между собой ограничениями. Например, если входное представление имеет размер W = 10, P = 0 и размер рецептивного поля F = 3, тогда использовать размер шага равный S = 2 становится невозможно, так как (W — F + 2P)/S + 1 = (10 — 3 + 0)/2 + 1 = 4.5, что даёт нецелочисленное значение количества нейронов. Таким образом подобная конфигурация гипер-параметров считается недействительной и библиотеки по работе со свёрточными нейронными сетями выбросят исключение, принудительно произведут выравнивание, либо вообще обрежут входное представление. Как мы увидим в следующих секциях данной главы, определение гипер-параметров свёрточного слоя доставляет ещё ту головную боль, которую можно уменьшить используя определённые рекомендации и "правила хорошего тона" при проектировании архитектуры свёрточных нейронных сетей.
Пример из реальной жизни. Архитектура свёрточной нейронной сети Krizhevsky et al., которая выиграла соревнование ImageNet в 2012 году принимала изображения размером 227х227х3. На первом свёрточном слое она использовала рецептивное поле размером F = 11, шаг S = 4 и размер выравнивания P = 0. Поскольку (227 — 11)/4 + 1 = 55, а свёрточный слой был глубиной K = 96, то выходная размерность представления была 55х55х96. Каждый из 55х55х96 нейронов в этом представлении был связан с областью размером 11х11х3 во входном представлении. Более того, все 96 нейронов в глубинном столбце связаны с такой же областью 11х11х3, но с другими весами. А теперь немного юмора — если вы решите ознакомиться с оригиналом документа (исследования), то обратите внимание, что в документе утверждается, что на вход поступают изображения размером 224х224, что не может быть правдой, потому что (224 — 11) / 4 + 1 никаким образом не дадут целочисленное значение. Подобного рода ситуации часто вводят в замешательство людей в историях со свёрточными нейронными сетями. По моим догадкам Алекс использовал размер выравнивания P = 3, но забыл упомянуть об этом в документе.
Совместное использование параметров. Механизм совместного использования параметров в свёрточных слоях используется для контроля количества параметров. Обратите внимание на приведённый выше пример, как можно увидеть там есть 55х55х96 = 290 400 нейронов на первом свёрточном слое и каждый из нейронов имеет 11х11х3 = 363 веса + 1 значение смещения. Суммарно, если перемножить эти два значения, получится 290400х364 = 105 705 600 параметров только на первом слое свёрточной нейронной сети. Очевидно, что это огромное значение!
Оказывается есть возможность значительно снизить количество параметров делая одно допущение: если некоторое свойство, вычисленное в позиции (x, y), имеет значение для нас, то это же свойство вычисленно в позиции (x2, y2) так же будет иметь для нас значение. Другими словами, обозначая двумерный "слой" в глубину как "глубинный слой" (например, представление [55x55x96] содежит 96 глубинных слоёв, каждый из которых размером 55х55), мы будем выстраивать нейроны в глубину с одними и теми же весами и смещением. При такой схеме совместного использования параметров первый свёрточный слой в нашем примере теперь будет содержать 96 уникальных наборов весов (каждый набора на каждый глубинный слой), всего будет 96х11х11х3 = 34 848 уникальных весов или 34 944 параметров (+96 смещений). Кроме того, все 55х55 нейронов на каждом глубинном слое будут теперь использовать те же параметры. На практике, во время обратного распространения, каждый нейрон в этом представлении будет вычислять градиент для собственных весов, но эти градиенты будут суммироваться по каждому глубинному слою и обновлять только единственный набор весов на каждом уровне.
Обратите внимание, если бы все нейроны на одном глубинном слое использовали одинаковые веса, то при прямом распространении через свёрточный слой вычислялась бы свёртка между значениями весов нейрона и входными данными. Именно поэтому принято называть единый набор весов — фильтром (ядром).

Примеры фильтров, которые были получены при обучении модели Krizhevsky et al. Каждый из 96 фильтров показанных тут размером 11х11х3 и каждый из них совместно используется всеми 55х55 нейронами одного глубинного слоя. Обратите внимание, что предположение о совместном использовании одних и те же весов имеет смысл: если детектирование горизонтальной линии важно в одной части изображения, то интуитивно понятно, что подобное детектирование важно и в другой части этого изображения. Поэтому нет никакого смысла каждый раз переобучаться находить горизонтальные линии в каждом из 55х55 различных мест изображения в свёрточном слое.
Стоит иметь ввиду, что допущение о совместном использовании параметров не всегда может иметь смысл. Например, в случае, если на вход свёрточной нейронно сети подаётся изображение с некоторой центрированной структурой, где бы мы хотели иметь возможность в одной части изображении обучиться одному свойству, а на другой части изображения — другому свойству. Практический пример — изображения с центрированными лицами. Можно предположить, что разные глазные признаки или признаки волос могут быть определены в различных областях изображения, поэтому в таком случае используется релаксация весов и слой называется локально связным.
Примеры с Numpy. Предыдущие обсуждения стоит перенести в плоскость конкретики и на примерах с кодом. Представьте, что входное представление это numpy-массив X. Тогда:
- Глубинный столбец (нить) на позиции
(x,y)будет представлен следующий образомX[x,y,:]. - Глубинный слой, или как мы ранее называли такой слой — карта активации на глубине
dбудет представлена следующим образомX[:,:,d].
Пример свёрточного слоя. Представим, что входное представление X имеет размеры X.shape: (11,11,4). Представим так же, что размер выравнивания P=1, размер рецептивного поля (фильтра) F=5 и шаг S=1. Выходное представление будет размером 4х4, исходя из значения формулы — (11-5)/2+1=4. Карта активации выходного представления (назовём её V), будет выглядеть таким образом (в этом примере представлены только несколько элементов):
V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0
Напоминаем, что в numpy, операция * относится к операции поэлементного умножения массивов. Обратите так же внимание, что вектор весов W0 является вектором весов нейрона и b0 его смещением. В нашем примере W0 имеет размеры W0.shape: (5,5,4), так как размер фильтра равен 5, а глубина равна 4. Как и при работе с обычными нейронными сетями мы вычисляем скалярное произведение между фильтром и соответствующей областью входного представления. Так же обратите внимание на тот факт, что мы используем одни и те же значения весов и смещений, а каждый раз смещаем рецептивное поле на 2 пикселя (размер шага). При построении второй карты активаций в выходном представлении у нас уже будет следующее:
V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1V[0,1,1] = np.sum(X[:5,2:7,:] * W1) + b1(пример, где мы смещаемся уже на осиy)V[2,3,1] = np.sum(X[4:9,6:11,:] * W1) + b1(пример, где мы смещаемся по обеим осям)
Таким образом мы формируем карту активации второго слоя — другие значения весов W1 и смещений b1. Мы намеренно упростили операции в примере, чтобы показать какие действия выполнить свёрточный слой для заполнения всех карт активаций выходного массива V. В дополнение имейте ввиду, что карты активации затем передаются на вход функции активации, например, ReLU, в которой осуществляется поэлементная обработка значений из карты. В примере этого мы не показали.
Резюме. Подводим итоги по свёрточному слою:
- Принимает на вход представление размером W1 x H1 x D1
- Требует 4 гипер-параметра:
- Количество фильтров K,
- их пространственные размер F,
- размер шага S,
- размер выравнивания P.
- Формирует результатирующее представление размером W2 x H2 x D2, где
- W2 = (W1 — F + 2P)/S + 1
- H2 = (H1 — F + 2P)/S + 1
- D2 = K
- С совместным использованием параметров формирует F x F x D1 весов на каждый фильтр, всего (F x F x D1) x K весов и K смещений.
- В выходном представлении,
d-слой (размера W2 x H2) представляет собой результат выполнения операции свёрткиd-фильтра над входным представлением с шагом S и затем смещённым на значениеd-смещения.
Стандартными значениями для гипер-параметров являются F = 3, S = 1, P = 1. Такие значения обоснованы рядом практических наблюдений и рекомендаций. Подробнее будет рассказано в разделе "Архитектура свёрточных нейронных сетей".
Демо. Чуть ниже мы показали пример работы свёрточного слоя. Так как 3D-представления сложно визуализировать (синий — входное представление, красное — веса, зеленое — выходное представление), мы представили каждый слой в виде стопок — один под другим. Размер входного представления W1 = 5, H1 = 5, D1 = 3, а параметры свёрточного слоя K = 2, F = 3, S = 2, P = 1. Итак, у нас есть два фильтра размером 3х3, которые применяются с шагом 2. Таким образом выходное представление будет иметь размер (5 — 3 + 2)/2 + 1 = 3. Более того, обратите внимание, что смещение P = 1 применяется ко входному представлению и дополняет его нулями. В визуализации ниже с правой стороны перемещается зеленый квадрат, который является результатом скалярного произведения части исходного представления (изображения) и фильтра, плюс значение смещения.
(здесь должна быть анимация, но она реализована на html+css в исходной странице, поэтому идём на исходную страницу и смотрим)
Реализация в виде матричного умножения. Операция свёртки основывается на скалярном произведении между значениями фильтра и локальной частью входного представления (изображения). Стандартным подходом к реализации свёрточного слоя является использование этого факта и реализация матричного умножения при прямом распространении следующим образом:
- Локальная область изображения выпрямляется в колонки операцией im2col. Например, если входные данные представляют собой изображение размером 227x227x3 к которому будет применена операция свёртки фильтром размером 11х11х3 и шагом 4, то и фильтр мы так же выпрямим в вектор размером 11х11х3 = 363 элемента. Повторяя данный процесс, каждый раз смещаясь на 4 пикселя по исходному представлению, мы получим (227 — 11) / 4 + 1 = 55 участков вдоль ширины и высоты, которые будут преобразованы и в результате получится выходная матрица X_col размером 363х3025, в которой каждая строка будет представлять собой выпрямленный фильтр и всего таких строк будет 3025. Обратите внимание, что значения пикселей, через которые проходит фильтр, дублируются (пересекаются), поэтому в результатирующей матрице будет много повторяющихся значений в различных строках.
- Веса свёрточного слоя выпрямляются в одномерный вектор таким же образом. Например, если у нас 96 фильтров размером 11х11х3, то в результате мы получим матрицу W_row размером 96х363.
- Результат операции свёртки теперь эквивалентен выполнению скалярного произведения полученных на предыдущих двух шагах матрицах — np.dot(W_row, X_col), которое вычисляет скалярное произведение каждого фильтра с каждым участком входного представления. В нашем примере размеры выходного представления будут равны 96х3025.
- Результат выполнения скалярного произведения теперь должен быть преобразован обратно в нужное представления размером 55х55х96.
У такого подхода, безусловно, можно заметить серьёзный недостаток — большой объём используемой памяти в связи с многократным дублированием значений при смещениях рецептивного поля, значения под которым пересекаются. Однако, несмотря на этот недостаток, у метода есть и преимущество — существует множество эффективных методов реализации матричного умножения (например, часто используемые в BLAS API). Более того, используемый нами метод im2col может быть использован повторно для выполнения операции подвыборки, которую мы обсудить чуть позже в этой главе.
Обратное распространение. Обратный проход (обратное распространение изменений) операции свёртки (как для входных данных, так и для весов) это тоже операция свёртки (только с пространственно-перевёрнутыми фильтрами). К такому умозаключение просто прийти, если рассмотреть одномерный вымышленный пример.
1х1 свёртка. Отойдём немного от нашей темы и рассмотрим свёртку размером 1х1, примеры использования которой впервые приводятся в Network in Network. Некоторые удивляются, когда впервые видят размер свёртки 1х1, особенно удивляются те, кто пришел с опытом в обработке сигналов. Обычно, сигналы представлены в 2-х мерном пространстве, поэтому свёртка 1х1 не имеет смысла (это всего лишь точечное изменение масштабов). Однако в свёрточных нейронных сетях всё обстоит совершенно иначе, потому что стоит всегда помнить о том, что в свёрточных нейронных сетях мы оперируем с 3-х мерным представлением, где фильтры применяются всегда по всей глубине входного представления. Например, если входное представление размером 32х32х3, а над ним выполняется операция свёртки с размером фильтра 1х1, то, по факту, мы выполняем скалярное произведение единичных значений по 3м измерениям (R, G, B — три канала, глубина).
Операция свёртки с расширением. Недавние исследования вводят ещё один гипер-параметр в свёрточные нейронные сети называемый расширением. До этого момента мы рассматривали свёрточные нейронные сети с непрерывными фильтрами. Однако можно использовать и фильтры у которых есть пробелы между ячейками, так называемые расширения. В качестве примера рассмотрим одномерный фильтр w размера 3 применённый к входному представлению x: w[0] x[0] + w[1] x[1] + w[2] x[2]. Это пример с расширением равным 0. При расширении равном 1 и применении фильтра мы получим следующий результат: w[0] x[0] + w[1] x[2] + w[2] x[4]. Другими словами в фильтре есть "дыра" в 1 значение между каждым элементом. Такой подход может быть крайне полезным в случаях, когда необходимо более агрессивно выделять пространственные признаки входного представления используя меньшее количество слоёв. Например, если расположить последовательно 2 свёрточных слоя размером 3х3, то можно убедиться в том, что второй слой нейронов будет являться функцией получающей на вход представление размером 5х5 (можем называть размер 5х5 эффективным рецептивным полем нейронов). При использовании расширений в операциях свёртки размер эффективных рецептивных полей будет очень быстро увеличиваться.
Слой подвыборки
Обычное дело — чередовать свёрточные слои в архитектуре свёрточной нейронной сети со слоями подвыборки. Задачей слоя подвыборки является снижение пространственных размеров входного представления, что приводит к снижению количества используемых параметров и сложности вычислений в самой сети, кроме этого слой подвыборки позволяет контролировать переобучение модели. Слой подвыборки применяется к каждому глубинному слою входного представления независимо, снижая его пространственные размеры используя операцию MAX. Наиболее распространен размер подвыборки 2х2 с шагом 2, который позволяет уменьшить каждый глубинный слой в 2 раза, исключая тем самым 75% активаций. Применение операции MAX в данном случае будет выбирать максимальное значение пикселя из поля размером 2х2. Количество глубинных слоёв остаётся неизменным. В обобщённом виде, слой подвыборки:
- Принимает представление размером W1 x H1 x D1
- Требует 2 гипер-параметра:
- размер рецептивного поля F,
- шаг S,
- Генерирует представление размером W2 x H2 x D2, где:
- W2 = (W1 — F)/S + 1
- H2 = (H1 — F)/S + 1
- D2 = D1
- Реализуется без параметров, так как выполняет фиксированную функцию над входным представлением
- Обычной практикой считается применение нулевых выравниваний (zero-padding по краям входного представления).
Стоит упомянуть о том, что на практике встречаются два наиболее распространенных варианта конфигурации слоёв подвыборки: слой подвыборки с F=3, S=2 (так же называемый пересекающейся подвыборкой), и более распространенный — F=2, S=2. Слои подвыборки с большими значениями гипер-параметров являются более деструктивными.
Операция подвыборки общего вида. Кроме операции подвыборки по максимальному значению, слой подвыборки может выполнять и другие операции, например, подвыборку по среднему значению или даже L2-подвыборку. Подвыборка по среднему значению использовалась на протяжении длительного времени, однако в последнее время начала вытесняться операцией подвыборки по максимальному значению, которая показала большую эффективность на практике.
| #1 | #2 |
|---|---|
 |
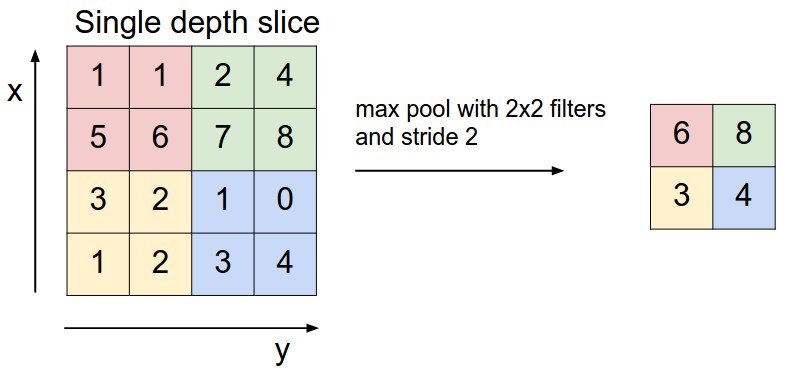 |
Слой подвыборки уменьшает пространственные размеры входного представления независимо друг от друга по каждому глубинному слою. Слева: в этом примере входное представление размером 224х224х64 подвергается применению операции подвыборки с размером фильтра 2х2 и шагом 2, формируя выходное представление размером 112х112х64. Обратите внимание, что количество глубинных слоёв осталось неизменным. Справа: наиболее частая операция подвыборки — по максимальному значению (max-pooling), здесь показана с размером шага 2. Максимальное значение выбирается из каждых 4 значений (небольшой области размером 2х2)
Обратное распространение. Вспомните из главы об обратном распространении, что обратное распространение операции max(a,b) имеет простую интерпретацию — перенос градиента входных данных у которого было максимальное значение при прямом распространении. Таким образом, во время прямого распространения через слой подвыборки имеет смысл хранить индекс максимального значения (иногда называется переключателем), чтобы при последующем обратном распространении вычислять градиент эффективно.
Избавляемся от подвыборки. Многим не нравится операция подвыборки и они считают, что от неё можно избавиться и отказаться в свёрточных нейронных сетях. Например, в статье Борьба за простоту: Свёрточные нейронные сети, предлагается избавиться от слоёв подвыборки и заменить их последовательностью свёрточный слоёв. Для уменьшения размера представления предлагают использовать большие размеры шагов в некоторых свёрточных слоях. Исключение слоёв подвыборки показало себя так же с хорошей стороны при тренировке генеративных моделей, таких как вариационные автокодировщики (VAEs) или генеративно состязательные сети (GANs). Кажется, что будущие архитектуры будут всё-таки без слоёв подвыборки, либо с малых количеством.
Слой нормализации
Много типов слоёв нормализации было предложено для использования в свёрточных нейронных сетях, иногда намеренно применяя такие архитектурные решения, которые наблюдаются в природе и биологическом мозге. Однако, эти слои со временем перестали использоваться, так как на практике выяснилась их минимальная эффективность и влияние на результат. Для углублённого рассмотрения типов нормализаций можно ознакомиться с этой статьёй.
Полносвязный слой
Нейроны в полносвязном слое связаны со всеми активационными нейронами предыдущего слоя, как это происходит в обычной нейронной сети. Их активационные значения могут быть вычислены через матричным произведением и добавлением значения смещения.
Преобразуем полносвяный слой в свёрточный слой
Стоит отметить, что единственной разницей между полносвязным слоем и свёрточным слоем является то, что нейроны в свёрточном слое связаны только с локальной областью входного представления и совместно используют параметры (веса и смещения). Однако нейроны в обоих слоях по-прежнему вычисляют скалярное произведение, а это значит что их функциональная структура идентична. Таким образом становится очевидно, что возможно преобразование между полносвязным слоем и свёрточным слоем:
- Для любого свёрточного слоя существует полносвязный слой, который реализует ту же функцию прямого распространения. Матрица весов, по больше части, будет заполнена нулями, кроме той области, которая является отображением локальных значений входного представления и значения в которой будут одинаковы в связи с тем фактом, что слои совместно используют веса.
- Напротив, любой полносвязный слой может быть преобразован в свёрточный слой. Например, полносвязный слой с K=4096 (количество фильтров), находящийся над областью размером 7х7х12 может быть эквивалентно представлен в виде свёрточного слоя с гипер-параметрами F=7, P=0, S=1, K=4096. Другими словами мы устанавливаем размеры фильтра таким образом, чтобы он соответствовал размерам входного представления и в таком случае выходное представление будет размерами 1х1х4096, давай идентичный результат начального полносвязного слоя.
Полносвяный слой в свёрточный слой. Из перечисленных двух преобразований, возможность преобразования полносвязного слоя в свёрточный слой является наиболее полезной на практике. Давайте рассмотрим на примере архитектуру свёрточной нейронной сети, которая на входе принимает изображение размером 224х224х3 и затем использует серию свёрточных слоёв и слоёв подвыборки для уменьшения размера изображения до размера активационных карт 7х7х512 (в архитектуре свёрточной нейронной сети AlexNet, как мы увидим позднее, это реализовано с использованием 5 слоёв подвыборки, которые снижают размерность изображения каждый раз в два раза до 7 — 224/2/2/2/2/2 = 7). После этого AlexNet использует два полносвязных слоя размером 4096 и, наконец, последний полносвязный слой с 1000 нейронов, которые вычисляют оценку по классу. Мы можем преобразовать каждый из этих трёх полносвязных слоёв в свёрточный слой как описано ниже:
- Заменить первый полносвязный слой, который "смотрит" на область размером 7х7х512, на свёрточный слой с размером фильтра F=7, что на выходе даст представление размером 1х1х4096.
- Заменить второй полносвязный слой на свёрточный слой с размером фильтра F=1, на выходе будет представление размером 1х1х4096.
- Заменить последний полносвязный слой таким же образом с размером фильтра F=1, на выходе будет представление размером 1х1х1000.
Каждое из этих преобразований, на практике, может включать и преобразование (изменение размеров и форм) матрицы весов W в каждом полносвязной слое в фильтр в свёрточном слое. Оказывается, что подобного рода преобразование позволяет нам "двигать" (перемещать) исходную свёрточную сеть очень эффективно по всем областям большого изображения за один проход.
Например, если при размерах изображения 224х224 на входе, получаем 7х7х512 на выходе — снижая размер в 32 раза, то подавая на вход изображение уже размером 384х384 можно получить на выходе представление размером 12х12х512, так как 384/32 = 12. Если проделать такую операцию с теми свёрточными слоями к которым при пришли в ходе преобразования полносвязных слоёв, то итоговый размер представления, после прохождения всех слоёв, будет равен 6х6х1000, так как (12 — 7)/1 + 1 = 6. Обратите внимание, что вместо единственного вектора с оценками размера 1х1х1000 мы получаем весь массив 6х6 оценок по всем 384х384 изображениям.
Подавая на вход исходной свёрточной нейронной сети (с полносвязными слоями) независимо все изображения размером 384х384, обрезанные до 224х244 с шагом 32 пикселя, даст те же результаты, что и единственный проход новой свёрточной нейронной сети.
Логично предположить, что подавая на вход сразу несколько изображений даёт прирост производительности и скорости вычислений, нежели последовательное вычисление во всех 36 точках, так как все 36 вычислений используют общие параметры. Этот трюк используется на практике для повышения производительности, например в тех случаях, где возникает необходимость изменять размеры изображения делая его больше. Использование новой архитектуры свёрточной нейронной сети позволяет вычислить оценки по классам во множестве пространственных позициях и затем усреднить их.
Что, если бы мы захотели более эффективно использовать исходную свёрточную нейронную сеть, но с шагом меньше 32 пикселей? Мы могли бы этого добиться через множественные прямые распространения (несколько итераций прямого распространения). Например, если бы мы захотели использовать шаг равный 16 пикселям, то могли бы это сделать через объединение представлений полученных при прямом распространении 2 раза: первый раз проведя преобразования над исходным изображением и второй раз над изображением смещённым на 16 пикселей вдоль ширины и высоты.
Архитектура свёрточных нейронных сетей
Как мы уже успели понять свёрточные нейронные сети, в основном, состоят из 3 различных типов слоёв: свёрточный слой, слой подвыборки (подразумеваем подвыборка по максимальному значению, если не отмечено другое) и полносвязный слой. Мы так же явно вынесем активационную функцию ReLU в отдельный слой, которая применяется по-элементно добавляя нелинейности. В этой части мы обсудим каким образом эти слои чередуются для формирования всей свёрточной нейронной сети.
Наиболее часто используемая архитектура свёрточной нейронной сети представляет собой последовательность нескольких CONV-RELU-слоёв, после них следует POOL-слой и подобная комбинация повторяется такое количество раз, пока исходное представление изображения не будет небольшого размера. В какой-то момент происходит переход к полносвязному слою. Последний полносвязный слой содержит выходные данные, например, оценки по классам. Другими словами, наиболее частая архитектура свёрточной нейронной сети выглядит так:
INPUT -> [[CONV -> RELU]*N -> POOL?] * M -> [FC -> RELU]*K -> FCгде операция * обозначает повторение, а POOL? обозначает опциональность слоя подвыборки. Более того, N >= 0 (обычно N <= 3), M >= 0, K >= 0 (обычно K < 3). Например, вот наиболее частые архитектуры свёрточных нейронных сетей, которые удовлетворяют приведённому выше паттерну:
INPUT -> FC, реализует линейный классификатор.N = M = K = 0.INPUT -> CONV -> RELU -> FCINPUT -> [CONV -> RELU -> POOL] * 2 -> FC -> RELU -> FC, тут мы видим наличие единственного свёрточного слоя между каждым слоем подвыборки.INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL] * 3 -> [FC -> RELU] * 2 -> FC. Тут мы уже видим 2 свёрточных слоя перед каждым слоем подвыборки. В целом, это хорошее решение для больших и глубоких сетей, потому что несколько подряд идущих свёрточных слоёв способны выделить более сложные признаки во входных данных перед деструктивной операцией подвыборки.
Выбирайте группировку нескольких свёрточных слоёв с небольшим размером фильтра нежели свёрточный слой с большим размером фильтра. Предположим что мы разместили подряд 3 свёрточных слоя размером 3х3 (с RELU слоем между ними, конечно же). В таком расположении каждый нейрон первого свёрточного слоя имеет "обзор" области размером 3х3 входного представления. Нейрон на втором слое имеет "обзор" области размером 3х3 уже выходного представления первого слоя, а с учетом выравнивания — размеры входного представления равны 5х5. Аналогичным образом нейрон на третем слое имеет "обзор" области 3х3 выходного представления уже второго слоя, с учетом выравнивания — размер области 7х7. Теперь представим, что вместо трёх свёрточных слоёв 3х3 мы хотели бы использовать один свёрточный слой с размером фильтра 7х7. У нейронов этого слоя был бы такой же "обзор" области 7х7 (с учетом выравниваний) как и у нашей предыдущей структуры, но с рядом недостатков. Во-первых, нейроны будут вычислять линейную функцию по входным данным, в то время как наши 3 подряд идущих свёрточных слоя содержат нелинейность, которая позволит сделать значимые признаки более заметными. Во-вторых, если мы предположим что все представления содержат C каналов, тогда можно заметить, что наш единственный 7х7 свёрточный слой будет содержать (Cх(7х7хС)) = 49xСxC параметров, в то время как три свёрточных слоя 3х3 будут содержать только 3х(Сх(3х3хС)) = 27хСхС параметра. Интуитивно становится понятно, что последовательное размещение свёрточных слоёв с небольшими фильтрами вместо размещения одного свёрточного слоя с большим размером фильтра, позволяет выделить больше значимых признаков из входных данных с меньшим количеством параметров. С практической точки зрения у такого подхода есть свой недостаток — необходимо больше памяти для хранения промежуточных результатов вычислений свёрточных слоёв, если мы планируем реализовывать обратное распространение.
Отступления. Стоит отметить тот факт, что последовательное расположение свёрточных слоёв подвергает испытаниям, в архитектурах свёрточных сетей от компании Google, а так же в архитектурах сетей от компании Microsoft. Обе из этих архитектур представляют собой более интересные структуры с разной организацией соединений между слоями.
На практике: используйте то, что наилучшим образом работает на наборах данных ImageNet. Если ты уже чувствуешь себя немного потерянным при мыслях о выборе подходящей архитектуры свёрточной нейронной сети, то будешь приятно удивлён, что в 90% случаев тебе не стоит об этом беспокоиться. Мне нравится выражение для данной ситуации — "не будь героем": вместо того, чтобы изобретать собственные архитектуры для решения задачи, стоит взглянуть на существующие решения и выбрать оптимальные, те которые работают наилучшим образом на наборах данных ImageNet — загрузить обученные модели, докрутить их на своих данных и использовать. Редко когда тебе понадобится обучать свёрточную нейронную сеть с нуля или проектировать архитектуру с нуля.
Паттерны при выборе размеров слоёв
До сих пор мы опускали вопрос выбора значений гипер-параметров, используемых в наших слоях в свёрточной нейронной сети. Сперва мы озвучим рекомендации, а затем перейдём к их обсуждению:
Входной слой (содержащий изображение) должен делиться на 2 множество раз. Стандартные значения включают 32 (например, CIFAR-10), 64, 96 (например, STL-10), или 224 (например, ImageNet), 384 и 512.
В свёрточном слое рекомендуется использовать фильтры небольшого размера (например, 3х3 или, максимум 5х5), с использованием шага S=1 и, что не менее важно, размером выравнивания таким образом, чтобы свёрточный слой не изменял пространственные размеры входного представления. Таким образом, F=3 и при P=1 будет возможность сохранить исходные пространственные размеры входного представления. При F=5, P=2. Для обобщённого размера F может быть определено, что при P=(F-1)/2 размеры исходного представления будут сохранены. Если по каким-то причинам необходимо использовать фильтры большего размера (такие как 7х7), то есть смысл использовать их только на первом слое свёрточной нейронной сети при работе с исходным изображением.
Слой подвыборки отвечает за снижение размерности входного представления. Наиболее частой конфигурацией является использование слоя подвыборки по максимальному значению размером 2х2 (F=2) и шагом 2 (S=2). Учтите, что подобная конфигурация исключает 75% активаций входного представления (из-за сэмплирования, в два раза по ширине и высоте). Другой, менее распространенной конфигурацией, является конфигурация с параметрами 3х3 (размер фильтр) и 2 (размер шага). Изредка вы увидите размеры фильтра больше 3х3 для слоя подвыборки, потому что подвыборка представляет собой очень агрессивную функцию при применении которой теряется информация по признакам. Такой подход обычно приводит к плохой производительности.
Уменьшаем головные боли при выборе значений размеров. Представленные выше рекомендации выглядят приятными, потому что все свёрточные слои сохраняют пространственные размеры входных представлений, а за уменьшение размеров представления отвечает слой подвыборки. При альтернативных значениях, где мы используем шаг больше 1 или не выполняем операцию выравнивания входных представлений, мы должны очень внимательно будем следить за размером входных представлений по мере прохождения через слои и убедиться в том, что всё работает как надо и архитектура свёрточной нейронной сети выровнена и симметрична.
Почему используют размер шага равный 1 в свёрточном слое? На практике меньшего размера шаги работают лучше. Как мы уже ранее отмечали, размер шага равный 1 позволяет делегировать сэмплирование входного представления слою подвыборки (изменение размеров входного представления по ширине и высоте), сохраняя за свёрточным слоем только преобразование в глубину.
Зачем использовать выравнивание? В дополнение к приведённым выше аргументу по сохранению размерности выходного представления после прохождения через свёрточный слой, выравнивание позволяет повысить производительность. Если бы свёрточные слои не использовали выравнивание входных представлений, а лишь выполняли операцию свёртки, тогда размер выходных представлений уменьшался бы каждый раз на небольшое количество пикселей, а информация на краях входного представления исчезала бы слишком быстро.
Компромиссы основанные на ограничениях памяти. В некоторых ситуациях (особенно на ранних стадиях развития архитектур свёрточных нейронных сетей), количество требуемой памяти может очень быстро увеличиваться, если следовать всем рекомендациям выше. Например, применяя три свёрточных слоя по 64 фильтра каждый с размером 3х3 и шагом 1 к изображению 224х224х3, создаст на выходе активационное представление размером 224х224х64. Это, примерно, равно 10 млн активаций, или 72 Мб памяти (на изображение, как для активаций так и для градиентов). Так как бутылочным горлышком в процессе вычислений является размер доступной памяти GPU, то приходится идти на компромиссы. На практике, одним из компромиссов может быть использование первого свёрточного слоя с размером фильтра 7х7 и шагом 2. Другой компромисс, как это сделано в AlexNet, использовать фильтр размером 11х11 и шагом 4.
Исследования существующих решений
Существует несколько архитектур свёрточных нейронных сетей у которых есть собственные имена. Вот некоторые из них:
- LeNet. Первая успешная реализация свёрточной нейронной сети была разработана Yann LeCun в 1990. Из них самой известной стала архитектура LeNet, которая использовалась для чтения ZIP-кодов, цифры и др.
- AlexNet. Первая работа, которая популяризовала свёрточные нейронные сети в компьютерном зрении, разработана Alex Krizhevsky, Ilya Sutskever и Geoff Hinton. AlexNet была протестирована на соревновании ImageNet ILSVRC в 2012 году и значительно опередила конкурента на втором месте (процент ошибок: 16% против 26%). Архитектура сети была очень похожа на архитектуру LeNet, но была глубже, больше и использовала последовательности свёрточных слоёв (до этого было стандартной практикой использоватье только комбинацию свёрточного слоя сразу за которым следовал слой подвыборки).
- ZFNet. Победителем ILSVRC 2013 года стала свёрточная нейронная сеть от Matthew Zeiler и Rob Fergus. Стала она известна под названием ZFNet. Это была усовершенствованная версия AlexNet, которая использовала другие значения гипер-параметров, в частности увеличивавшая размер среднего свёрточного слоя и уменьшавшая шаг и размер фильтра на первом свёрточном слое.
- GoogLeNet. Победителем ILSVRC 2014 года стала свёрточная нейронная сеть от Szegedy et al. из Google. Основным изменением в архитектура стал Inception-модуль, который позволял значительно снизить количество параметров в сети (4 Мб против 60 Мб в AlexNet). В добавок к этому сеть использует подвыборку по среднему значению вместо полносвязных слоёв к концу сети, исключая тем самым большое количество параметров, которые не имеют большого значения. У данной версии сети есть несколько модификаций, одна из последних — Inveption-v4.
- VGGNet. Вслед за победителем 2014 ILSVRC была сеть от Karen Simonyan и Andrew Zisserman, которая стала так же известна как VGGNet. Основным вкладом этой нейронной сети в развития представлений о свёрточных нейронных сетях был тот факт, что глубина сети является ключевым компонентом хорошей производительности. Финальная версия их сети содержала 16 пар свёрточныйх + полносвязных слоёв и использовала единые размеры фильтров (3х3 для свёртки и 2х2 для операции подвыборки). Их предобученная модель находится в публичном доступе и с ней можно поэкспериментировать. Обратная сторона медали VGGNet — стоимость вычислений и использование большого количества памяти (140Мб). Большинство из этих параметров находятся на первом полносвязном слое и, как было в дальнейшем изучено и протестировано, эти полносвязные слои могут быть исключены без влияния на производительность, но с колоссальным уменьшением количества требуемых параметров.
- ResNet. Residual-сеть была разработана Kaiming He et al. и стала победителем в ILSVRC 2015. Она активно использует пропуск связей и блоковую нормализацию. В архитектуре так же отсутствуют полносвязные слои в конце сети. На данный момент это лучшее решение с использованием свёрточных нейронных сетей (на май 2016).
VGGNet в деталях. Давайте рассмотрим VGGNet подробнее в качестве эксперимента. Вся сеть VGGNet состоит из свёрточных слоёв, которые выполняют операцию свёртки с применением фильтра размером 3х3, шагом 1 и выравниванием 1, слой подвыборки с конфигурацией размера фильтра 2х2 и шагом 2. Мы можем зафиксировать размер представлений на каждом шаге выполнения (прохождения через слои свёрточной нейронной сети) и общее количество весов:
INPUT: [224x224x3] memory: 224*224*3=150K weights: 0
CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*3)*64 = 1,728
CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*64)*64 = 36,864
POOL2: [112x112x64] memory: 112*112*64=800K weights: 0
CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*64)*128 = 73,728
CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*128)*128 = 147,456
POOL2: [56x56x128] memory: 56*56*128=400K weights: 0
CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*128)*256 = 294,912
CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824
CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824
POOL2: [28x28x256] memory: 28*28*256=200K weights: 0
CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*256)*512 = 1,179,648
CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296
CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296
POOL2: [14x14x512] memory: 14*14*512=100K weights: 0
CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296
POOL2: [7x7x512] memory: 7*7*512=25K weights: 0
FC: [1x1x4096] memory: 4096 weights: 7*7*512*4096 = 102,760,448
FC: [1x1x4096] memory: 4096 weights: 4096*4096 = 16,777,216
FC: [1x1x1000] memory: 1000 weights: 4096*1000 = 4,096,000
TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd)
TOTAL params: 138M parametersКак это обычно наблюдается при работе со свёрточными нейронными сетями, обратите внимание на то, что большая часть памяти (и время вычислений) приходятся на ранние свёрточные слои, а большинство параметров находятся на последних полносвязных слоях. В данном конкретном случае полносвязный слой содержит 100 млн весов из всех 140 млн.
Вычислительные примечания
Самым узким местом при конструировании архитектур свёрточных нейронных сетей является память. Многие современные GPU ограничены 3/4/6 Гб памяти, а лучшие GPU — 12 Гб памяти. Три основных источника затрат по памяти, которые стоит иметь ввиду:
- Промежуточные представления: общее количество активаций на каждом свёрточном слое в свёрточной нейронной сети, а так же их градиенты (такого же размера). Обычно, большинство активаций приходится на ранние слоя. Они остаются в архитектуре потому что используются при обратном распространении, но более продвинутые реализации значительно уменьшают количество активаций благодаря хранению только текущих активаций на любом слое и не храня активации на всех предыдущих слоях ниже.
- Размеры параметров: параметры, которые хранят значения сети, их градиенты во время обратного распространения и размеры шагов. Таким образом количество памяти, требуемое для хранения только вектора параметров, обычно стоит умножать на х3 или более.
- Реализация каждой свёрточной нейронной сети должна ещё поддерживать возможность хранения других данных, вроде данных самого изображения и его анализируемых копий блоков, возможно перевёрнутые версии изображений и т.д.
Как только у вас появляется грубая оценка общего количества значений (активаций, градиентов и прочих), то это значение должно быть приведено к размеру в Гб. Возьмите количество полученных значений, умножайте его на 4 для получения количества байт (каждое значение с плавающей точкой занимает 4 байта, при использовании значений с двойной точностью — на 8), а затем разделите полученное значение на 1024 несколько раз, чтобы получить сперва Кб, затем Мб и в конце Гб. Если сеть "не помещается", то стандартной практикой сжатия является уменьшение размеров блоков, так как большая часть памяти приходится на активации.
… и стандартные call-to-action — подписывайся, ставь плюс и делай share :)
YouTube
Telegram
ВКонтакте
Комментарии (3)

nikolay_karelin
19.06.2019 22:51+1Немного комментариев: статья довольно старая, после 2014 много чего пояаилось. И я бы свертки рассказывал от цифровых фильтров, которые в том же фотошопе уже лет 20 с лишним работают.


AndrewShmig Автор
Минусующие, будьте добры, дайте обратную связь.
kahi4
Мне тоже интересно причины минусов, покуда я только зацепился за
Нейронным сетям, в целом, все равно сколько у них "измерений" при расположении нейронов, это их не делает сверточными. Ровно как и сверточные сети не обязательно сети, ориентированные на изображение и у них не всегда двухмерные (+цвет, трехмерные, простите) данные на входе (им, в целом, тоже все равно, сколько мерные вход).
Сверточные сети — это нейронные сети, у которых у одного или нескольких слоев нейроны, фактически, так же являются нейронными сетями сами по себе, в целом, являющимися ядрами свертки. Одно из самых прогрессивных и важных достижений — эти самые ядра видят только часть входных данных, при этом они все одинаковые и обучаются одновременно. Из-за того, что они все одинаковые — не требуется много ресурсов на их обучение.
Представить можно себе на разборе речи: самый нижний уровень — нейронные сети, которые способны распознавать отдельные звуки (заметим, что не нейроны, а именно нейронные сети, причем все одинаковые), затем их выходы являются входом сетей, способные распознавать слоги (опять же, весь слой может иметь 10 вложенных нейронных сетей, которые одинаковы, но подключены к разным входам), их обрабатывают сети, способные распознавать слова, ну и потом уже предложения.
Могу предположить, что минусы как раз из-за того, что везде описывается обычная нейронная сеть и упускается самое важное — что ядра — это нейронные сети сами по себе, повторенные кучу раз. Эдакий фильтр Канни. Вместо этого говорится, что к одному входному нейрону подключено лишь небольшое количество входных данных, а не весь предыдущий слой, что, в целом, является ключевой характеристикой сверточных нейронных сетей и сверточных же слоев, но не достаточной.