В предыдущей статье о модельно-ориентированном проектировании было показано, зачем нужна модель объекта, и доказано, что без этой модели объекта про model based design можно говорить только как о маркетинговой пурге, бессмысленной и беспощадной. Но при появлении модели объекта у грамотных инженеров всегда возникает резонный вопрос: какие есть доказательства, что математическая модель объекта соответствует реальном объекту.

Один из примеров ответа на этот вопрос приведен в статье про модельно-ориентированное проектирование электропривода. В этой статье мы рассмотрим пример создания модели для авиационных систем кондиционирования воздуха, разбавив практику некоторыми теоретическими соображениями общего характера.
Создание достоверной модели объекта. Теория
Чтобы не тянуть резину, сразу расскажу про алгоритм создания модели для модельно-ориентированного проектирования. В нем всего три простых шага:
Шаг 1. Разработать систему алгебро-дифференциальных уравнений, описывающих динамическое поведение моделируемой систем. Это просто, если знать физику процесса. Множество ученых уже разработали для нас основные физические законы имени Ньютона, Бренули, Навье Стокса и прочих Штангелей Циркулей и Рабиновичей.
Шаг 2. Выделить в полученной системе набор эмпирических коэффициентов и характеристик объекта моделирования, которые можно получить из испытаний.
Шаг 3. Провести испытания объекта и настроить модель по результатам натурных экспериментов, так чтобы она соответствовала реальности, с нужной степенью детализации.
Как видите, просто, как раз два три.
Пример практической реализации
Система кондиционирования воздуха (СКВ) в самолете связана с системой автоматического поддержания давления. Давление в самолете должно быть всегда больше внешнего давления, при этом скорость изменения давления должна быть такой, чтобы у летчиков и пассажиров не шла кровь носом и ушами. Поэтому система управления притоком и оттоком воздуха является важной для безопасности, и для ее разработки на земле ставят дорогостоящие системы испытаний. В них создают температуры и давления высоты полета, воспроизводят режимы взлета и посадки на аэродромах разной высоты. И вопрос разработки и отладки систем управления для СКВ встает в полный рост. Сколько времени мы будем гонять испытательный стенд, чтобы получить удовлетворительную систему управления? Очевидно, если мы настроим модель управления на модели объекта, то цикл работ на испытательном стенде может быть значительно сокращен.
Авиационная система кондиционирования воздуха состоит из таких же теплообменных аппаратов, как и любая другая тепловая система. Батарея – она и в Африке батарея, только кондиционер. Но из-за ограничения взлетной массы и габаритов летательных аппаратов теплообменники делаются как можно более компактными и как можно более эффективными, чтобы с меньшей массы передать как можно больше тепла. В итоге, геометрия становится достаточно причудливой. Как например в рассматриваемом случае. На рисунке 1 представлен пластинчатый теплообменник, у которого в между пластинами для улучшения теплообмена используется мембрана. Горячий и холодный теплоноситель чередуются в каналах, при этом направление течения – поперечное. Один теплоноситель подается на фронтальный срез, другой – на боковой.
Для решения задачи управления СКВ нам нужно знать, сколько передается тепла от одной среды к другой в таком теплообменнике в единицу времени. От этого зависит скорость изменения температуры, которую мы и регулируем.
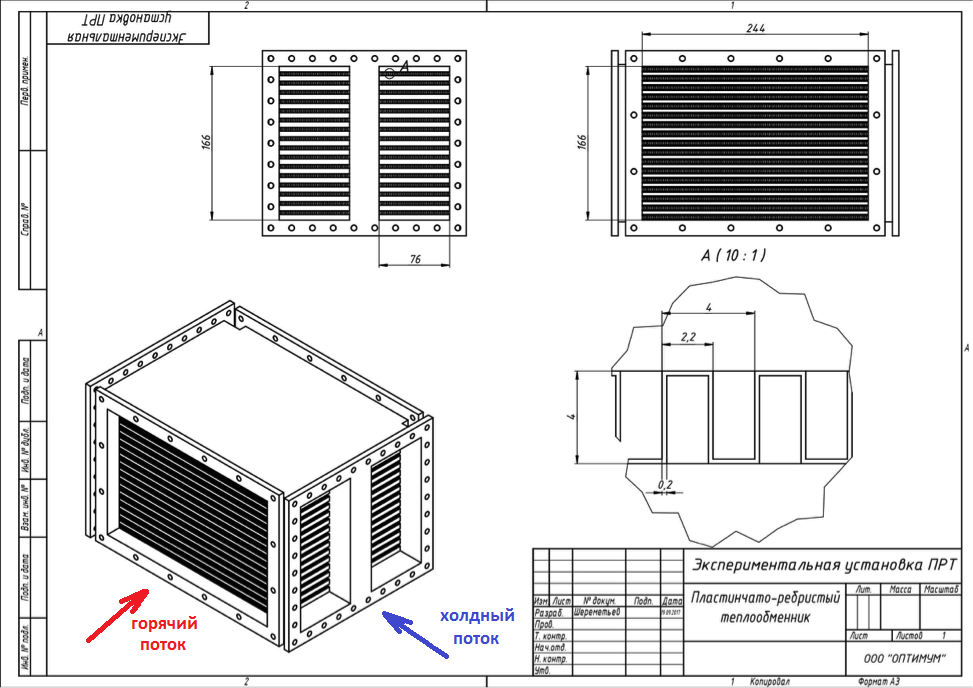
Рисунок 1. Схема авиационного теплообменного аппарата.
Проблемы моделирования. Гидравлическая часть
На первый взгляд задача достаточно простая, необходимо рассчитать массовый поток, по каналам теплообменника и тепловой поток между каналами.
Массовый расход теплоносителя в каналах рассчитывается про формуле Бернули:

где:
?P – перепад давления между двумя точками;
? – коэффициент трения теплоносителя;
L – длинна канала;
d – гидравлический диаметр канала;
? – плотность теплоносителя;
? – скорость теплоносителя в канале.
Для канала произвольной формы гидравлический диаметр рассчитывается по формуле:
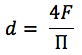
где:
F – площадь проходного сечения;
П – смоченный периметр канала.
Коэффициент трения, рассчитывается по эмпирическим формулам и зависит от скорости течения и свойств теплоносителя. Для разных геометрий получаются разные зависимости, например формула для турбулентного течения в гладких трубах:
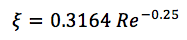
где:
Re – число Рейнольдса.
Для течения в плоских каналах можно использовать следующую формулу:

Из формулы Бернули можно рассчитать перепад давления для заданной скорости, либо наоборот рассчитать скорость теплоносителя в канале, по заданному перепаду давления.
Теплообмен
Тепловой поток между теплоносителем и стенкой рассчитывается по формуле:
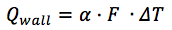
где:
? [Вт/(м2?град)] – коэффициент теплоотдачи;
F – площадь проходного сечения.
Для задач течения теплоносителей в трубах, проведено достаточное количество исследований и существует множество расчетных методик, и как правило все сводится к эмпирическим зависимостями, для коэффициента теплоотдачи ? [Вт/(м2?град)]
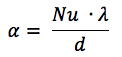
где:
Nu – число Нуссельта,
? – коэффициент теплопроводности жидкости [Вт/(м?град)]
d – гидравлический (эквивалентный) диаметр.
Для расчёта числа (критерия) Нусселта используются эмпирические критериальные зависимости, например формула для расчёта числа Нуссельта круглой трубы выглядит так:
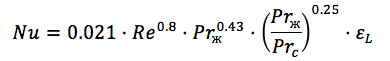
Здесь мы уже видим еще число Рейнолодса, число Прандтля при температуре стенки и температуре жидкости и коэффициент неравномерности. (Источник)
Для пластинчатых гофрированных теплообменников формула похожа ( Источник ):
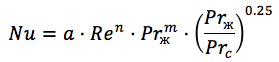
где:
n = 0.73 m =0.43 для турбулентного течения,
коэффициент а – меняется в пределах 0,065 до 0.6 в зависимости от количества пластин и режима течения.
Учтем, что данный коэффициент рассчитывается только для одной точки в потоке. Для следующей точки у нас другая температура жидкости (она нагрелась или охладилась), другая температура стенки и, соответственно, плывут все числа Рейнольдса, числа Прандтля.
На этом месте любой математик скажет, что посчитать точно систему, в которой коэффициент меняется в 10 раз невозможно, и будет прав.
Любой инженер-практик скажет, что каждый теплообменник отличается при изготовлении и посчитать системы невозможно, и тоже будет прав.
А как же модельно-ориентированное проектирование? Неужели все пропало?
Продвинутые продавцы западного софта в этом месте будут впаривать вам СуперЭВМ и системы 3D-расчёта, типа «без него никак». И нужно запускать расчет на сутки, чтобы получить распределение температур в течение 1 минуты.
Понятно, что это не наш вариант, нам нужно отлаживать систему управления, если не в реальном времени, то хотя бы в обозримом.
Решение методом тыка
Изготавливается теплообменник, проводится серия испытаний, и задается таблица эффективности установившейся температуры при заданных расходах теплоносителей. Просто, быстро и достоверно, поскольку данные получены с испытаний.
Недостаток такого подхода – нет динамических характеристик объекта. Да, мы знаем, какой будет установившийся тепловой поток, но не знаем, за какое время он установится при переходе с одного на другой режимы работы.
Поэтому, рассчитав необходимые характеристики, мы систему управления настраиваем непосредственно на испытаниях, чего нам изначально хотелось бы избежать.
Модельно-ориентированный подход
Для создания модели динамического теплообменника необходимо использовать данные испытаний, для устранения неопределенностей в эмпирических формулах расчета – числа Нуссельта и гидравлического сопротивления.
Решение просто, как все гениальное. Мы берем эмпирическую формулу, проводим эксперименты и определяем значение коэффициента a, тем самым, устраняя неопределенность в формуле.
Как только у нас появилось определенное значение коэффициента теплоотдачи, все остальные параметры определяются основными физическими законами сохранения. Разность температур и коэффициент теплопередачи определяют количество энергии, передаваемое в канал в единицу времени.
Зная поток энергии, можно решать уравнения сохранения массы энергии, и импульса для теплоносителя в гидравлическом канале. Например такое:
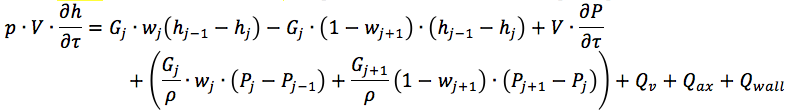
Для нашего случая, неопределённым остается поток тепла между стенкой и теплоносителем — Qwall. Подробнее можно посмотреть здесь...
А так же уравнение производной температуры для стенки канала:
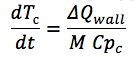
где:
?Qwall – разница входящего и исходящего потока на стенку канала;
M – масса стенки канала;
Cpc – теплоемкость материала стенки.
Точность модели
Как было сказано выше, в теплообменнике у нас есть распределение температуры по поверхности пластины. Для установившегося значения можно брать среднее по пластинам и использовать его, представив весь теплообменник в виде одной сосредоточенной точки, в которой на одном перепаде температур происходит передача тепла через всю поверхность теплообменника. Но для переходных режимов такое приближением может не работать. Другая крайность –сделать несколько сотен тысяч точек и нагрузить Супер ЭВМ, что тоже нам не подходит, поскольку стоит задача настраивать систему управления в реальном режиме времени, а лучше быстрее.
Возникает вопрос, на сколько участков нужно разбить теплообменник, чтобы получить приемлемую точность и скорость расчёта?
Как всегда случайно у меня под рукой оказалась модель аминового теплообменника. Теплообменный аппарат представляет собой трубчатку, в трубах течет греющая среда, между торбами – подогреваемая. Для упрощения задачи всю трубчатку теплообменника можно представить в виде одной эквивалентной трубы, а саму трубу представить в виде набора дискретных расчетных ячеек, в каждой из которых происходит расчет точечной модели теплообмена. Схема модели одной ячейки приведена на рисунке 2. Канал горячего воздуха и канал холодного воздуха соединены через стенку, которая обеспечивает передачу теплового потока между каналами.
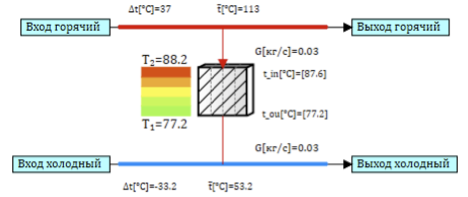
Рисунок 2. Модель ячейки теплообменника.
Модель трубчатого теплообменника легко настраивается. Можно менять всего один параметр – количество участков по длине трубы и посмотреть на результаты расчётов при разных разбиениях. Проведем расчет нескольких вариантов, начиная с разбиения на 5 точек по длине (рис. 3) и до 100 точек по длине (рис. 4).
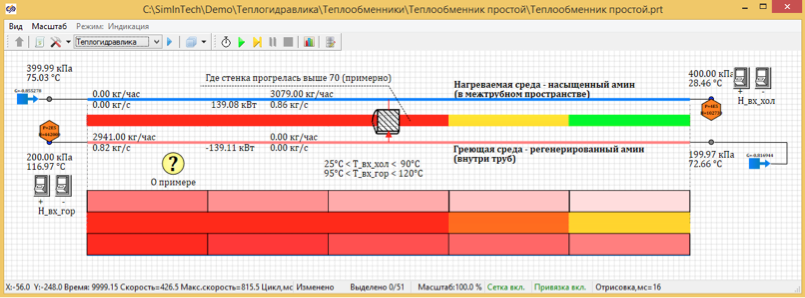
Рисунок 3. Стационарное распределение температуры 5 расчетных точек.
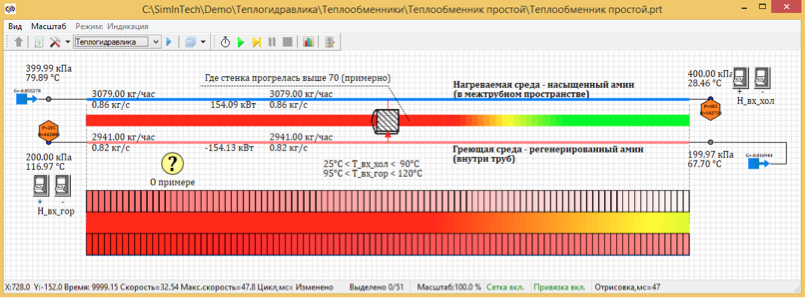
Рисунок 4. Стационарное распределение температуры 100 расчетных точек.
В результате расчетов получилось, что установившаяся температура при разбиении на 100 точек составляет 67,7 град. А при разбиении на 5 расчетных точек температура составляет 72, 66 град С.
Также в нижней части окна выводится скорость расчёта относительно реального времени.
Посмотрим, как меняется установившаяся температура и скорость расчёта в зависимости от количества расчетных точек. Разницу установившихся температур при расчетах с разным количество расчетных ячеек можно использовать для оценки точности полученного результата.
Таблица 1. Зависимость температуры и скорости расчета от количества расчетных точек по длине теплообменника.
| Кол-во расчетных точек | Установившаяся температура | Скорость расчёта |
| 5 | 72,66 | 426 |
| 10 | 70.19 | 194 |
| 25 | 68.56 | 124 |
| 50 | 67.99 | 66 |
| 100 | 67.8 | 32 |
Анализируя данную таблицу, можно сделать следующие выводы:
- Скорость расчёта падает пропорционально количеству расчётных точек в модели теплообменного аппарата.
- Изменение точности расчета происходит экспоненциально. При увеличении количества точек уточнение на каждом следующем увеличении снижается.
В случае пластинчатого теплообменника с перекрёстным током теплоносителя, как на рисунке 1, создание эквивалентной модели из элементарных расчетных ячеек слегка усложняется. Нам нужно соединить ячейки таким образом, чтобы организовать перекрёстное течения. Для 4 ячеек схема будет выглядеть так, как представлено на рисунке 5.
Течение теплоносителя разделяется по горячей и холодной ветке на два канала, каналы соединятся через тепловые структуры, таки образом чтобы при прохождении по каналу теплоноситель обменивался теплом с разными каналами. Моделируя перекрёстное течение, горячий теплоноситель идет слева на право (см. рис. 5) в каждом канале, последовательно обмениваясь с теплом с каналами холодного теплоносителя, который идет снизу вверх (см. рис. 5). Самая горячая точка находится в левом верхнем углу, поскольку горячий теплоноситель обменивается теплом с уже нагретым теплоносителем холодного канала. А самая холодная в правом нижнем, где холодный теплоноситель обменивается теплом с горячим теплоносителем, уже остывшим на первом участке.
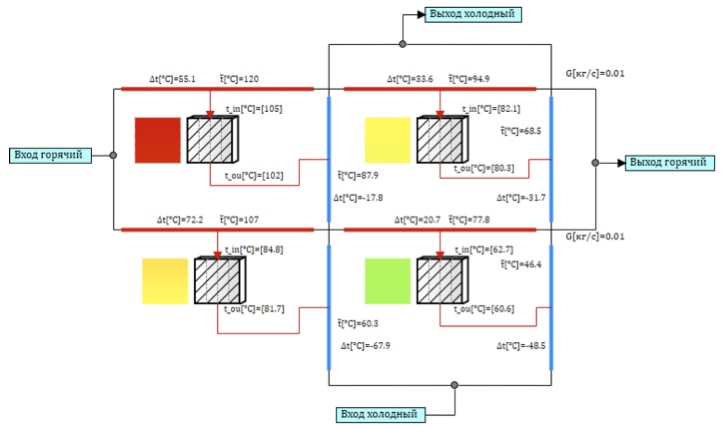
Рисунок 5. Модель поперечного потока из 4 расчетных ячеек.
Такая модель для пластинчатого теплообменника не учитывает перенос тепла между ячейками за счет теплопроводности и не учитывает перемешивание теплоносителя, так как каждый канал изолированный.
Но в нашем случае последнее ограничение не уменьшает точность, поскольку в конструкции теплообменника гофрированная мембрана разделяет поток на множество изолированных каналов по теплоносителю (см. рис. 1). Посмотрим, что происходит с точностью расчета при моделировании пластинчатого теплообменника при увеличении количества расчетных ячеек.
Для анализа точности мы используем два варианта разбиения теплообменника на расчетный ячейки:
- Каждая квадратная ячейка содержит два гидравлических (холодный и горячий потоки) и один тепловой элемент. (см. рисунок 5)
- Каждая квадратная ячейка содержит шесть гидравлических элементов (по три участка в горячем и холодном потоках) и три тепловых элемента.
В последнем случаем мы используем два вида соединения:
- встречное течение холодного и горячего потоков;
- попутное течение холодного и горячего потока.
Встречное течение увеличивает эффективность по сравнению с перекрёстным, а попутное течение уменьшает. При большом количестве ячеек происходит усреднение по потоку и все становится близко к реальному поперечному обтеканию (см. рисунок 6).
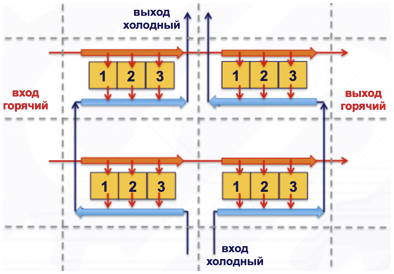
Рисунок 6. Модель поперечного потока из четырех ячеек с 3-я элементами.
На рисунке 7 приведены результаты установившегося стационарного распределения температуры в теплообменнике при подаче по горячей линии воздуха с температурой 150 °С, а по холодной линии – 21 °С, для различных вариантов разбиения модели. Цветом и цифрами на ячейке отражается средняя температура стенки в расчетной ячейке.
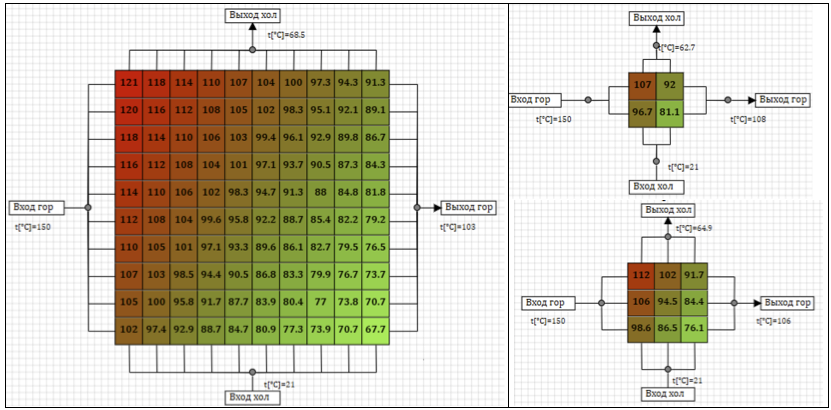
Рисунок 7. Установившиеся температуры для разных расчетных схем.
В таблице 2 приведена установившаяся температура подогретого воздуха после теплообменника в зависимости от разбиения модели теплообменника на ячейки.
Таблица 2. Зависимость температуры от количества расчетных ячеек в теплообменнике.
| Размерность модели | Установившаяся температура 1 элемент в ячейке |
Установившаяся температура 3 элемента в ячейке |
| 2х2 | 62,7 | 67.7 |
| 3x3 | 64.9 | 68.5 |
| 4х4 | 66.2 | 68.9 |
| 8х8 | 68.1 | 69.5 |
| 10x10 | 68.5 | 69.7 |
| 20x20 | 69.4 | 69.9 |
| 40x40 | 69.8 | 70.1 |
При увеличении количества расчетных ячеек в модели происходит рост конечной установившейся температуры. Разницу между установившейся температурой при разных разбиениях можно рассматривать как показатель точности расчёта. Видно, что при увеличении количества расчетных ячеек температура стремится к пределу, и рост точности не пропорционален количеству расчетных точек.
Возникает вопрос, а какая точность модели нам нужна?
Ответ на это вопрос зависит от назначения нашей модели. Поскольку в данной статье речь идет про модельно-ориентированное проектирование, то модель мы создаем для настройки системы управления. Это значит, что точность модели должна быть сопоставима с точностью датчиков, используемых в системе.
В нашем случае температура измеряется термопарой, у которой точность составляет ±2.5°С. Любая точность выше для целей настройки системы управления бесполезна, наша реальная система управления просто ее «не увидит». Таким образом, если принять, что предельная температура при бесконечном числе разбиений – 70 °С, то достаточной точности будет модель, которая дает нам больше 67.5 °С. Все модели с 3 точками в расчетной ячейке и модели больше 5х5 с одной точкой в ячейке. (Выделенные зеленым в таблице 2)
Динамические режимы работы
Для оценки динамического режима оценим процесс изменения температуры в самой горячей и холодной точках стенки теплообменника для разных вариантов расчетных схем. (см. рис. 8)
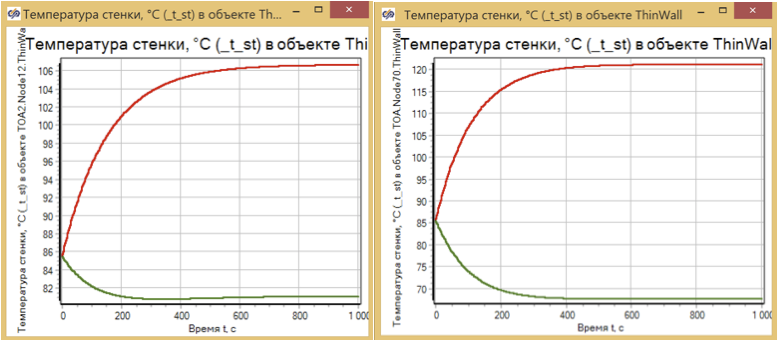
Рисунок 8. Прогрев теплообменника. Модели размерности 2х2 и 10х10.
Видно, что время переходного процесса и сам его характер, практически не зависят от количества расчетных ячеек, и определяются исключительно массой прогреваемого металла.
Таким образом, делаем вывод, что для честного моделирования теплообменника в режимах от 20 до 150 °С, с точностью, необходимой системе управления СКВ, достаточно порядка 10 – 20 расчетных точек.
Настройка динамической модели по эксперименту
Имея математическую модель, а так же данные эксперимента по продувке теплообменника, нам остается сделать простую коррекцию, а именно, ввести коэффициент интенсификации в модель, такой чтобы расчет совпадал с результатами эксперимента.
Более того, используя графическую среду создания модели, мы сделаем это автоматически. На рисунке 9 представлен алгоритм подбора коэффициентов интенсификации теплообмена. На вход подаются данные, полученные из эксперимента, подключается модель теплообменника, и на выходе получаются необходимые коэффициенты для каждого из режимов.
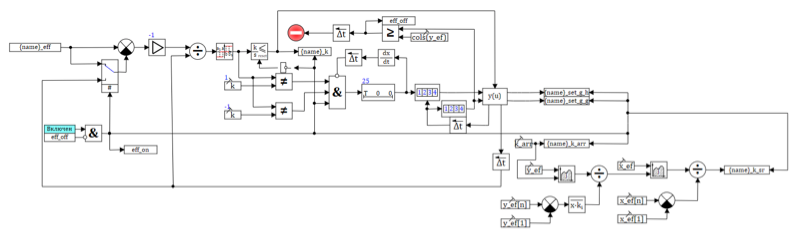
Рисунок 9. Алгоритм подбора коэффициента интенсификации по результатам эксперимента.
Таким образом мы определяем тот самый коэффициент для a числа Нуссельта и устраняем неопределенность в формулах расчета. Для различных режимов работы и температур значения поправочных коэффициентов могут меняться, однако для схожих режимов работы (нормальной эксплуатации) они оказываются весьма близкими. Например, для данного теплообменника для различных режимов коэффициент составляет от 0.492 до 0.655
Если применить коэффициент 0.6, то в исследуемых режимах работы погрешность расчета будет меньше погрешности термопары, таким образом, для системы управления математическая модель теплообменника будет полностью адекватной настоящей модели.
Результаты настройки модели теплообменника
Для оценки качества теплообмена используется специальная характеристика – эффективность:
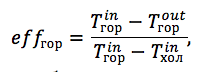
где:
effгор – эффективность теплообменника по горячему теплоносителю;
Tгорin – температура на входе в теплообменник по тракту движения горячего теплоносителя;
Tгорout – температура на выходе их теплообменника по тракту движения горячего теплоносителя;
Tхолin – температура на входе в теплообменник по тракту движения холодного теплоносителя.
В таблице 3 приведены значения отклонения эффективности модели теплообменника от экспериментальной при различных расходах по горячей и холодной линиям.
Таблица 3. Погрешности расчёта эффективности теплообмена в %
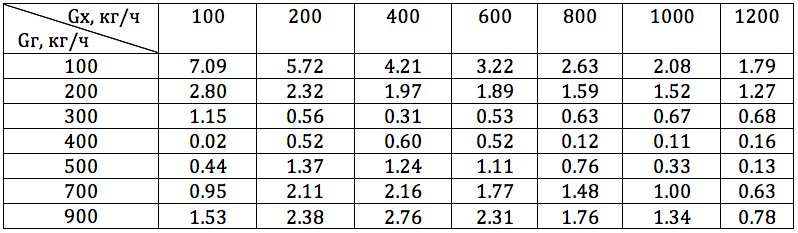
В нашем случае подобранный коэффициент может быть использован во всех интересуемых нас режимах работы. В случае если при низких расходах, где погрешность больше, необходимая точность не достигается, мы можем использовать переменный коэффициент интенсификации, который будет зависеть от текущего расхода.
Например, на рисунке 10 коэффициент интенсификации рассчитывается по заданной формуле в зависимости от текущего расхода в ячейках канала.
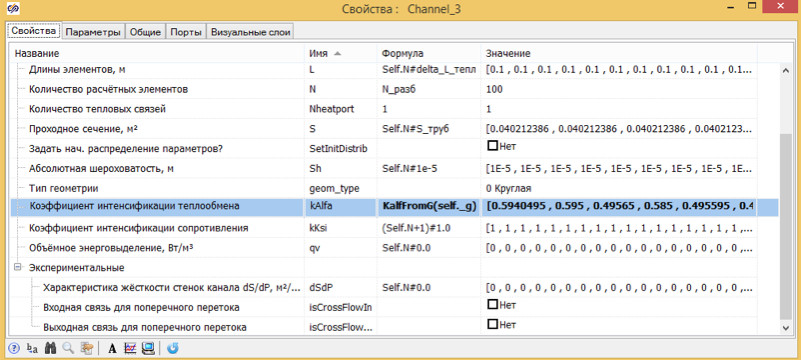
Рисунок 10. Переменный коэффициент интенсификации теплообмена.
Выводы
- Знание физических законов позволяет создавать динамические модели объекта для модельно-ориентированного проектирования.
- Модель должна быть верифицирована и настроена по данным испытаний.
- Средства разработки моделей должны позволять разработчику настраивать модель по результатам испытаний объекта.
- Используйте правильный модельно-ориентированный подход и будет вам счастье!
Бонус для тех кто дочитал. Видео работы виртуальной модели системы СКВ.
Комментарии (20)

KonstantinSpb
10.09.2019 22:57Я так понимаю, что следующая статья будет про Hardware in the loop, судя по результатам голосования.
A real control system - how to start designing





KonstantinSpb
А если физика процесса неизвестна или просто лень с системой диффуров заморачиваться на первых этапах, то можно сделать System identification в Матлабе
petuhoff Автор
Если физика объекта не известна, то это не проектирование от слова совсем.
И если вы систему идентифицировали, в диапазонах на которых были данные, то при выходе за диапазон никто не гарантирует результата.
KonstantinSpb
Да, верно. Поэтому диапозон входных данных должен быть максимально возможным.
System Identification больше напоминает reverse engineering физических процессов.
petuhoff Автор
А здесь возникает вопрос испытаний. В данном случае, я должен в теплообменник загнать воздух с температурой высоты 10 км это -50, плюс для работы System Identification, вы должны мерить не просто точку с установившееся режимом, а скорость перехода из состояние в состояние, с учетом инерционность термопар, сложности настройки оборудования, получить идеальное воздействие для переходного процесса вообще отдельная наука.
KonstantinSpb
Да, инерционность(тау) is a bitch.
Разумеется замеры должны быть максимально непрерывными с достаточной частотой сэмплирования
petuhoff Автор
в SimInTech это тоже есть, но для реальных проектов, все таки лучше смотреть на процессы, понимая физику или хотя бы приближаясь к ней