02.02.2021 21:10
petuhoff 43 5400 Источник

В продолжение темы модельно ориетированного проектирования, публикую очередную статью Калачева Юрия Николаевича, автора книги Моделирование в электроприводе. Инструкция по пониманию. Данный текст еще готовится к публикации в специализированных изданиях, но читатели хабра увидят его первые.

В зарубежной литературе можно встретить два термина, связанных с этими двигателями:

  1. PMSM (Permanent Magnet Synchronous Motor), что на языке Пушкина означает: синхронный двигатель c постоянными магнитами (СДПМ), и это понятно.

  2. BLDC (Brush Less Direct Current), что переводится с языка Шекспира, как Бесколлекторный (бесщеточный) Двигатель Постоянного Тока (БДПТ), и это непонятно. Причем здесь постоянный ток?

С этими названиями и у нас, и за рубежом существует немалая путаница.

Например, термин PMSM (СДПМ) может применяться для обозначения двигателя с постоянными магнитами на роторе, независимо от формы его ЭДС, но так же часто его применяют, подразумевая исключительно синусоидальную форму ЭДС двигателя.

Термин BLDC (БДПТ) может применяться для обозначения двигателя с постоянными магнитами на роторе и трапецеидальной ЭДС, а может вообще обозначать не двигатель, а некий мехатронный узел, включающий в себя:

  • двигатель с постоянными магнитами и трапецеидальной ЭДС

  • датчик положения ротора

  • управляемый по сигналам этого датчика полупроводниковый коммутатор.

Собственно этот мехатронный узел, который может, как и двигатель постоянного тока, управляться постоянным напряжением и породил сам термин BLDC (БДПТ).

Ещё по отношению к синхронным двигателям с постоянными магнитами на роторе в отечественной литературе, можно встретить название «вентильный двигатель».

Попытки автора разобраться с этим термином быстро зашли в тупик, так как в различных источниках обнаружились явные противоречия.

Например, в книге Г.Б. Онищенко «Электрические двигатели» на стр. 47 «вентильным» называется двигатель соответствующий термину BLDC (БДПТ), что предполагает трапецеидальную ЭДС, и это понимаемо.

Но двигатели типа 5ДВМ сам производитель (ЧЭАЗ) называет «вентильными», хотя при этом утверждает, что они имеют синусоидальную ЭДС.

А вот википедия: «Вентильный двигатель следует отличать от бесколлекторного двигателя постоянного тока (БДПТ), который имеет трапецеидальное распределение магнитного поля в зазоре...».

Ну, ... приехали ...

Какой термин, какой форме ЭДС соответствует – непонятно.

А между тем, именно эта форма определяет выбор структуры системы управления двигателем.

Как человек занимающийся управлением этими двигателями хочу предложить:

  • во избежание путаницы забыть термин «вентильный двигатель»

  • термином БДПТ обозначать не двигатель, а исключительно описанный выше мехатронный узел (аналог двигателя постоянного тока)

  • делить синхронные двигатели с постоянными магнитами на роторе (СДПМ) по типу ЭДС на две группы:

    1) с синусоидальной ЭДС (далее, для краткости, - СДПМс)

    2) с трапецеидальной ЭДС (далее, для краткости, - СДПМт)

Управление

При управлении двигателями с синусоидальной ЭДС используется векторное регулирование (подробно описано в книжке по ссылке). С точки зрения возможностей и качества управления это наилучший вариант.

Однако и двигатели с трапецеидальной ЭДС в силу более простой конструкции статорных обмоток и возможности более простого управления применяются довольно часто.

Конструкция двигателей

Ротор синхронных двигателей обоих типов устроен одинаково. Он представляют собой магнит с различным количеством пар полюсов.

А вот конструкция статорных обмоток, которая собственно и определяет форму ЭДС, у разных типов различна (см. Рис 1.).

Рисунок 1. Конструкции статорных обмоток
Рисунок 1. Конструкции статорных обмоток

Статорная обмотка двигателя с трапецеидальной ЭДС проще и технологичнее, за счёт этого цена такого двигателя несколько ниже.

Далее остановимся более подробно на двигателе с трапецеидальной ЭДС (СДПМт)

Двигатель с одной парой полюсов будет выглядеть в разрезе так, как показано на Рис.2.

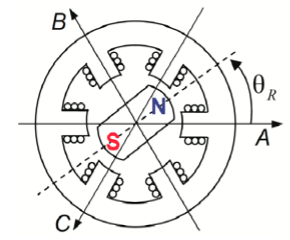
Рисунок 2. Схема двигател с одной парой полюсов я в разрезе
Рисунок 2. Схема двигател с одной парой полюсов я в разрезе

На статоре СДПМт намотаны три обмотки (А, В, С), сдвинутые в пространстве на 120°. Каждая обмотка состоит из двух секций, включённых встречно. Таким образом, при протекании тока в обмотке она создаёт внутри двигателя два полюса (положительный и отрицательный), к которым и притягивается магнитный ротор. Поочередное изменение токов в обмотках переключает полюса обмоток и заставляет ротор двигаться вслед за полем. На этом и основан принцип работы двигателя.

В дальнейшем будем считать нулевым то угловое положение ротора \theta_Rпри котором вектор потока ротора совпадает по направлению с осью фазы А (осью обмотки А).

Уравнения равновесия статорных обмоток СДПМт в системе АВС

Уравнения равновесия статорных обмоток двигателя при его включении в «звезду» в неподвижных фазных координатах АВС имеют вид (1).

\left \{ \begin{gathered} U_{A\Phi} =\frac{d \Psi_А}{dt} + I_AR_{\Phi} \\U_{B\Phi} =\frac{d \Psi_B}{dt} + I_BR_{\Phi} \\U_{C\Phi} =\frac{d \Psi_C}{dt} + I_CR_{\Phi}\ \end{gathered} \right. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(1)}

Здесь:

  • U_{A \Phi},U_{B\Phi},U_{C\Phi} - фазные напряжения

  • \Psi_A,\Psi_B,\Psi_c- потокосцепления фазных обмоток

  • I_A,I_B,I_C- токи фаз

  • R_\Phi- активное сопротивление фазной обмотки.

Поток в обмотке каждой фазы формируется из следующих составляющих:

  • поток, наводимый собственным током фазы

  • поток, наводимый магнитными полями других фазных обмоток 

  • поток, наводимый в обмотке магнитами ротора.

Проиллюстрируем это системой (2):

\left \{ \begin{gathered} \Psi_{A} = L_AI_A+L_{AB}I_B+L_{AC}I_C +\Psi_{fA}\\ \Psi_{B} = L_BI_B+L_{AB}I_A+L_{BC}I_C+\Psi_{fB} \\ \Psi_{C} = L_CI_C+L_{AC}I_A+L_{BC}I_B+\Psi_{fC} \end{gathered} \right. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(2)}

  • Где:

    L_{A},L_{B},L_{C} - индуктивность фазных обмоток

    L_{AB},L_{BC},L_{AC} - взаимные индуктивности обмоток

    \Psi_{fA},\Psi_{fB},\Psi_{fC}- потокосцепления, наводимые в обмотках магнитом ротора.

В общем случае все индуктивности системы (2) могут являться переменными функциями угла поворота поля ?_e.

В частном случае для неявнополюсного двигателя (при цилиндрическом роторе) индуктивности и взаимные индуктивности обмоток не зависят от угла.

Обозначив
L_\Phi- индуктивность фазной обмотки,

L_{\Phi\Phi} - взаимная индуктивность двух фазных обмоток,
и подставив выражения (2) в систему (1), получим выражение (3):

\left \{ \begin{gathered} U_{A\Phi} =L_\Phi\frac{d I_А}{dt}+L_{\Phi\Phi}\frac{d I_B}{dt}+L_{\Phi\Phi}\frac{d I_C}{dt}+\frac{d \Psi_{fA}}{dt} + I_AR_{\Phi} \\ U_{B\Phi} =L_\Phi\frac{d I_B}{dt}+L_{\Phi\Phi}\frac{d I_A}{dt}+L_{\Phi\Phi}\frac{d I_C}{dt}+\frac{d \Psi_{fB}}{dt}+ I_BR_{\Phi}\\ U_{C\Phi} =L_\Phi\frac{d I_C}{dt}+L_{\Phi\Phi}\frac{d I_A}{dt}+L_{\Phi\Phi}\frac{d I_B}{dt}+\frac{d \Psi_{fC}}{dt}+ I_СR_{\Phi}\ \end{gathered} \right. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3)}

Заметив, что производные по времени от потокосцеплений магнитов ротора

\left(\frac{d \Psi_{fA}}{dt},\frac{d \Psi_{fB}}{dt},\frac{d \Psi_{fС}}{dt}\right) - есть не что иное, как наводимая магнитами

ротора в этих обмотках ЭДС, систему (3) можно переписать в виде (4).

\left \{ \begin{gathered} U_{A\Phi} =L_\Phi\frac{d I_А}{dt}+L_{\Phi\Phi}\frac{d I_B}{dt}+L_{\Phi\Phi}\frac{d I_C}{dt}+E_A + I_AR_{\Phi} \\ U_{B\Phi} =L_\Phi\frac{d I_B}{dt}+L_{\Phi\Phi}\frac{d I_A}{dt}+L_{\Phi\Phi}\frac{d I_C}{dt}+E_B+ I_BR_{\Phi}\\ U_{C\Phi} =L_\Phi\frac{d I_C}{dt}+L_{\Phi\Phi}\frac{d I_A}{dt}+L_{\Phi\Phi}\frac{d I_B}{dt}+E_C+ I_СR_{\Phi}\ \end{gathered} \right. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4)}

Теперь введем понятие единичной функции формы ЭДС.

Единичная функция формы ЭДС - это функция от угла поля (?_e), имеющая единичную амплитуду и повторяющая по форме ЭДС. Для фаз А,В,С обозначим эти функции: E_{1A},E_{1B},E_{1C}.

Используя единичные функции формы, мгновенные ЭДС в фазах можно представить выражением (5):

\left \{ \begin{gathered} E_{A} = \psi_f\omega_eE_{1A}=\psi_fZ_p\omega_RE_{1A} \\ E_{B} = \psi_f\omega_eE_{1B}=\psi_fZ_p\omega_RE_{1B} \\ E_{C} = \psi_f\omega_eE_{1C}=\psi_fZ_p\omega_RE_{1C} \end{gathered} \right. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5)}

  • Где:

    \psi_f- амплитуда потокосцепления ротора и фазной обмотки

    \omega_e- скорость вращения поля 

    \omega_R- скорость вращения ротора

    Z_P- число пар полюсов двигателя.

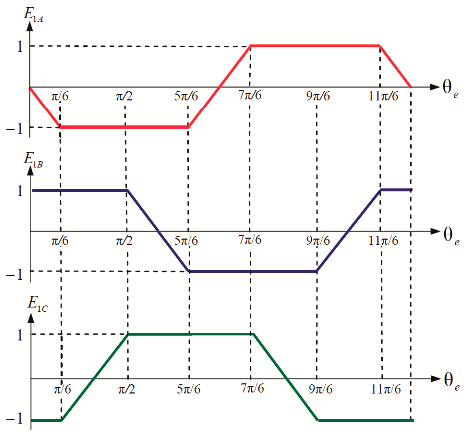
Зависимости единичных функций формы ЭДС обмоток СДПМт от угла поворота поля представлены На Рис.3.

Рис. 3. Единичные функции форм ЭДС
Рис. 3. Единичные функции форм ЭДС

Вывод формулы для расчета электромагнитного момента СДПМт

Момент, создаваемый двигателем, является суммой моментов, создаваемых его обмотками.

Посмотрим на уравнение равновесия обмотки А из системы (4).

U_{A\Phi} =L_\Phi\frac{d I_A}{dt}+L_{\Phi\Phi}\frac{d I_B}{dt}+L_{\Phi\Phi}\frac{d I_C}{dt}+E_A + I_AR_{\Phi}

Умножив обе его части на ток обмотки, получим уравнение для мгновенной электрической мощности обмотки:

P_{A\Phi} =I_A \left( L_\Phi\frac{d I_A}{dt}+L_{\Phi\Phi}\frac{d I_B}{dt}+L_{\Phi\Phi}\frac{d I_C}{dt}\right ) + I_A^2R_{\Phi}+I_AE_A

Рассмотрим составляющие этой мощности:

  • I_A \left( L_\Phi\frac{d I_A}{dt}+L_{\Phi\Phi}\frac{d I_B}{dt}+L_{\Phi\Phi}\frac{d I_C}{dt}\right)- реактивная мощность обмотки

  • I_A^2R_{\Phi} - активная мощность, рассеивающаясяв обмотке

  • I_AE_A- мощность, создающая электромагнитный момент.

Если пренебречь потерями при переходе электрической мощности в механическую, то можно записать:

I_AE_A + I_BE_B+I_CE_C = M_{em}\omega_R \Rightarrow M_{em} =\frac{I_AE_A + I_BE_B+I_CE_C}{\omega_R} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6)}

  • Где:

    M_{em}- электромагнитный момент двигателя

    \omega_R - угловая скорость вращения ротора.

Подставив в формулу (6) значения ЭДС из соотношений (5), получим формулу вычисления электромагнитного момента ротора (7).

M_{em} =\psi_fZ_p \left(I_AE_{1A} + I_BE_{1B}+I_CE_{1C}\right) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7)}

Коммутация обмоток СДПМт

В соответствии с формулой (7) момент СДПМт пропорционален сумме произведений фазных токов на функции формы соответствующих ЭДС.

Максимальное значение ЭДС обмотки соответствует плоским участкам трапеции ЭДС. Если бы нам удалось на этих участках угловой траектории сформировать в обмотках токи некоторой постоянной амплитуды, например, совпадающие по знаку со знаком ЭДС, то это позволило бы сформировать при этих токах максимальный постоянный положительный момент.

Для примера рассмотрим на Рис.3 участок угловой траектории от ?/6 до ?/2. На этом участке ЭДС в фазе А имеет максимально отрицательное значение, а в фазе В максимально положительное. Следовательно, для получения положительного момента на этом участке угловой траектории надо обеспечить в фазе А отрицательное, а в фазе В положительное значение тока. Для этого фазу А можно подключить на отрицательный, а фазу В на положительный полюса внешнего источника постоянного напряжения (Udc). При этом фаза С не используется (отключена от источника Udc).

Величина тока, протекающего через обмотки, будет в свою очередь определяться прикладываемым к обмоткам напряжением, величиной ЭДС и параметрами обмоток.

Если рассуждать таким образом, то можно составить таблицу коммутаций обмоток, обеспечивающих в зависимости от положения ротора момент нужного знака (Табл. 1).

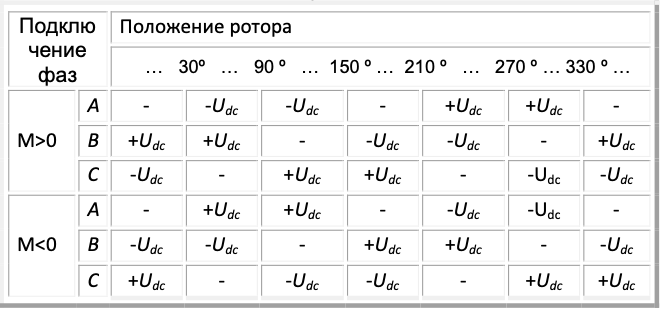
Таблица1. Закон коммутации
Таблица1. Закон коммутации

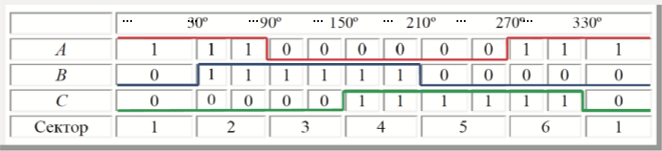
Обмотки трёхфазного двигателя можно коммутировать на внешний источник напряжения с помощью трехфазного мостового инвертора. Для этого состояние инвертора надо поставить в зависимость от положения ротора. Обычно это делается с помощью датчика положения ротора (ДПР). Этот датчик имеет три канала. Каждый канал выдает за один оборот двигателя импульс, соответствующий половине периода вращения, при этом импульсы в каналах сдвинуты на 120°.

Логическая обработка сигналов ДПР позволяет определить - в каком из шести секторов в данный момент находится ротор.

Работа ДПР поясняется Табл. 2.

Таблица 2. Работа ДПР (определение сектора)
Таблица 2. Работа ДПР (определение сектора)

Возможная структура системы управления моментом СДПМт

Алгоритм, описанный в Табл.1, предполагает протекание одного и того же тока в двух фазах двигателя при единичном значении функции формы ЭДС в обмотках фаз. Поэтому выражение (7) можно переписать в виде (8).

M_{em} =2 \cdot Z_p\psi_fI_\Phi \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8)}

Где: I_\Phi- значение тока в фазах.

То есть значение момента пропорционально величине тока в обмотках двигателя.

Вытекающая из формулы (8) структура системы управления моментом в приводе с СДПМт изображена на Рис.4.

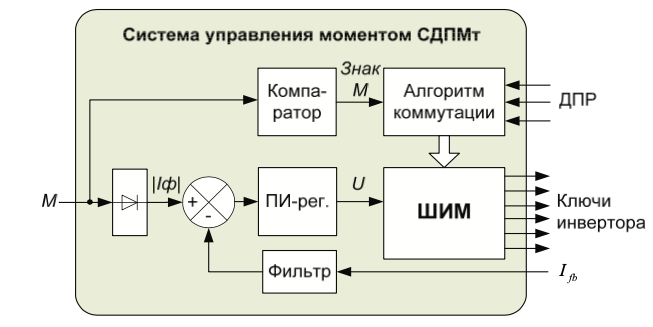
Рисунок 4. Система управления моментом БДПТ
Рисунок 4. Система управления моментом БДПТ

Данная структура позволяет получить нужный момент, формируя в обмотках двигателя ток необходимой амплитуды, при сохранении алгоритма коммутации (Табл.1).

Эта задача решается с помощью создания на базе трёхфазного мостового инвертора контура тока с ШИМ.

Регулятор тока (ПИ-рег.) формирует сигнал задания напряжения обмоток (U), которое затем реализуется инвертором с ШИМ в соответствии с алгоритмом коммутации (Табл.1).

В качестве сигнала обратной связи в контуре можно использовать трёхфазно-выпрямленные сигналы датчиков тока фаз или сигнал датчика тока в звене постоянного тока инвертора (I_{fb}).

На основе рассмотренного канала управления моментом можно строить внешние контуры управления скоростью и положением.

Однако

Если бы токи в обмотках спадали до нуля и нарастали до нужного уровня мгновенно, то момент двигателя, определяемый их величиной, в установившемся режиме был бы постоянным. В действительности же реальные переходные процессы при коммутации обмоток приводят к пульсациям момента. В зависимости от параметров обмоток, а также соотношения величин текущей ЭДС и напряжения звена постоянного тока эти пульсации могут быть различны по длительности, амплитуде и знаку.

Кроме этих коммутационных пульсаций в рассматриваемой системе также будут иметь место пульсации момента на частоте ШИМ.

Ниже приведен пример работы модели системы регулирования скорости. Данная модель построена в среде SimInTech на элементах специализированного тулбокса «Электропривод». Среда позволяет получить максимальное приближение моделируемых процессов к реальности с учетом эффектов временной и уровневой дискретизации.

Часть модели, а именно - модель цифровой системы управления скоростью приведена ниже, на Рис.5. Регулятор скорости системы (Рег.W) выдает сигнал момента, который отрабатывается структурой, построенной в соответствии с Рис.4.

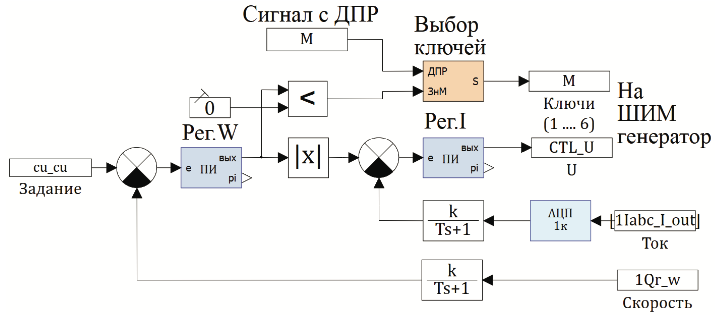
Рисунок 5. Модель цифровой системы управления
Рисунок 5. Модель цифровой системы управления

Для управления был выбран двигатель со следующими параметрами:

  • Rs = 2.875 Ом - сопротивление обмотки фазы;

    Ls = 8.5e-3 Гн – индуктивность фазы;

    F = 0.175 Вб – потокосцепление ротора;

    Zp = 4 - число пар полюсов;

    Jr = 0.06 н·м - момент инерции ротора.

Напряжение в звене постоянного тока привода было принято равным 100В.

В контуре тока электропривода использовалась ШИМ с частотой 5кГц.

В процессе регулирования происходило ступенчатое увеличение частоты при постоянном моменте сопротивления на валу двигателя (10 Нм).

Графики, полученные в процессе работы модели, приведены на Рис.6.

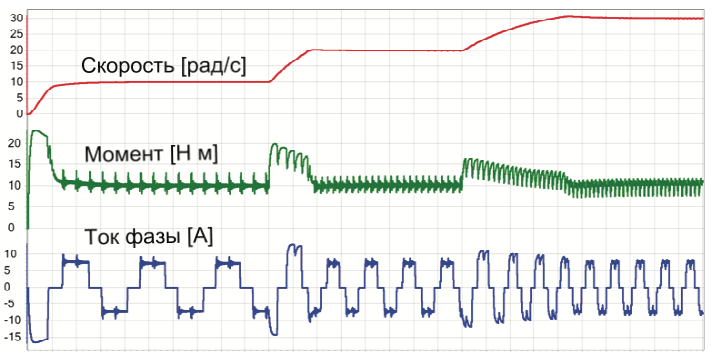
Рисунок 6. Моделирование работы двигателя
Рисунок 6. Моделирование работы двигателя

На графике момента видны существенные пульсации.

Отметим, что в основном они связаны именно с переходными процессами при коммутации обмоток и имеют соответственно частоту, ушестеренную по отношению к заданной.

Пульсации, связанные с ШИМ, в данном случае, невелики.

Заметим, что коммутационные пульсации существенно возрастают при увеличении момента, что связано с увеличением тока.

Несколько спасает то, что их влияние на скорость снижает инерция.

А можно ли векторно управлять СДПМт?

Если очень хочется - то можно.
Однако и здесь не без особенностей.
Математика и структура стандартной векторной системы управления исходит из синусоидальности поля в зазоре. При трапецеидальной ЭДС это условие нарушается, правда не очень сильно (трапеция это же почти синус).

А результатом этого «почти» будут, опять же, пульсации момента.

Вид модели цифровой системы векторного управления скоростью в среде SimInTech показан на Рис.7.

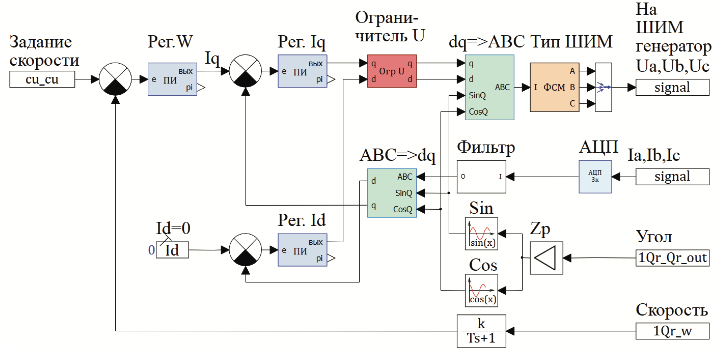
Рисунок 7. Часть модели векторного управления.
Рисунок 7. Часть модели векторного управления.

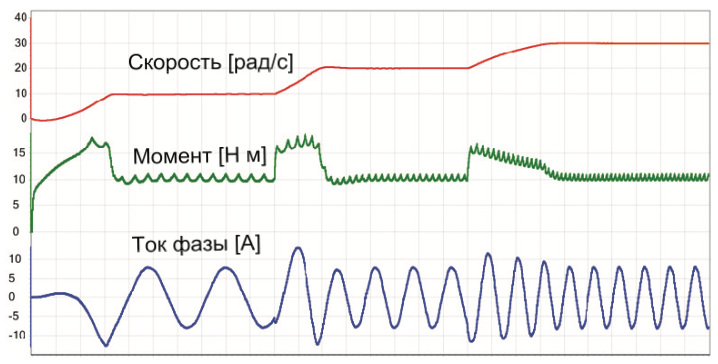
Ниже на Рис.8 показан график работы модели уже рассмотренного ранее СДПМт работающего в рассмотренном ранее режиме, но под управлением векторной системы.

В графике момента мы опять наблюдаем пульсации (хотя по сравнению с предыдущим вариантом они несколько уменьшились).

Причины пульсации при векторном управлении и управлении по ДПР различны, но частота все та же – ушестеренная по отношению к заданной.

Заметим, что вследствие несинусоидальности ЭДС токи в обмотках двигателя так же будут принципиально несинусоидальными (это так, хотя в масштабе рисунка и не слишком заметно).

Рисунок 8. Работа двигателя при векторном управлении
Рисунок 8. Работа двигателя при векторном управлении

А можно ли с помощью коммутации обмоток по ДПР управлять двигателем с синусоидальной ЭДС?

С точки зрения автора можно – но не нужно.

Наряду с коммутационными пульсациями момента синусоидальность ЭДС (отсутствие плоской вершины трапеции) в данном случае неминуемо вызовет еще и дополнительные пульсации, снижающие качество регулирования даже по сравнению с управляемым по ДПР двигателем СДПМт.

А при векторном управлении двигателем с синусоидальной ЭДС пульсаций момента не будет.

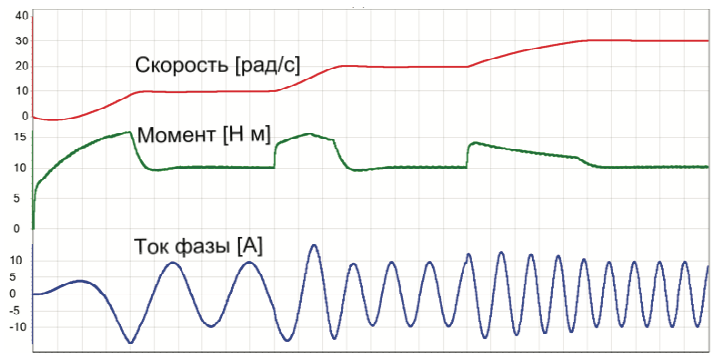
Для подтверждения этого тезиса ниже (Рис.9) приведены графики работы модели двигателя с уже рассмотренными ранее параметрами, но с синусоидальной ЭДС и векторной системой управления скоростью.

Видно, что пульсации момента в этом случае практически отсутствуют. При правильной настройке регуляторов системы они связаны только с ШИМ-преобразованием и для данного случая почти не видны.

Рисунок 8. Работа двигателя с синусоидальной ЭДС
Рисунок 8. Работа двигателя с синусоидальной ЭДС

Итоги

Для синхронников с трапецеидальной ЭДС - коммутация по ДПР.

Так же возможно использование и более сложного векторного алгоритма регулирования, что может дать снижение уровня пульсации момента.

Для синхронников с синусоидальной ЭДС лучший вариант это векторное регулирование.

Это сочетание идеально для построения точного электропривода (что собственно и так было понятно).

Калачёв Ю.Н.

Модели для самостоятельного изучения можно взять здесь.

Предыдущие статьи по теме:

Модельно ориентированное проектирование. Электропривод с бесколлекторным двигателем постоянного тока

Модельно ориентированное проектирование. Построение активного выпрямителя (на основе математической модели)

Список литературы

[1] А. С. Пушкин «Полтава».