07.04.2021 04:32
petuhoff 19 1700 Источник

Колебательное звено является наиболее интересным случаем из всех типовых звеньев, во-первых, за счет “сильной похожести” по своим динамическим свойствам на более сложные реальные САУ (САР), во-вторых, близкой идентичности переходных процессов в звене к аналогичным в реальных САР, и, в-третьих, существенной зависимости динамических свойств от величины параметра звена.

Выведем формулу колебательного звена на примере электрического колебательного контура, который изучают в курсе школьной физики. Пример такого контура приведен на рисунке 3.5.1

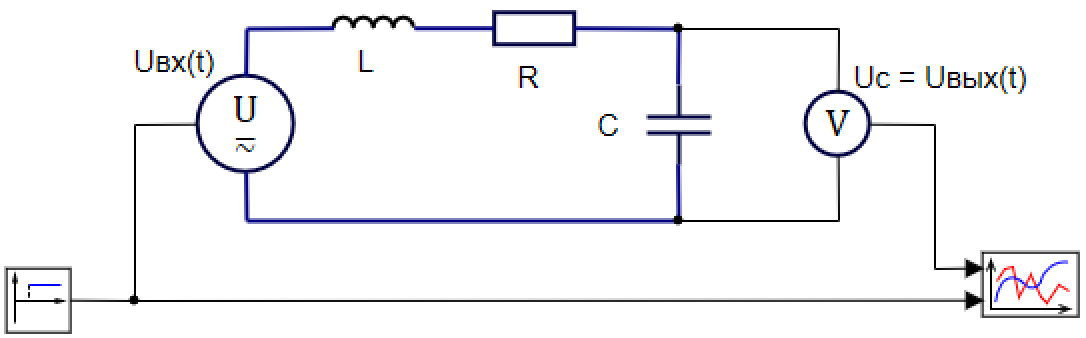
Рисунок 3.5.1 Модель электического колебательного контура
Рисунок 3.5.1 Модель электического колебательного контура

Электрическая цепь содержит источник напряжения и последовательно соединённые индуктивность, сопротивление, конденсатор.

Входное ступенчатое воздействие x(t), формирующее внешнюю Э.Д.С в цепи, подключено к блоку «источнику напряжения» х(t) = Uвх(t). 

Результирующий отклик звена - напряжение на конденсаторе y(t) = Uс(t) = Uвых(t).

Согласно второму закону Кирхгофа для замкнутого контура, сумма Э.Д.С равна сумме напряжения на резистивных элементах контура.

U_R+U_C =U_{вх} +\xi_L \Rightarrow \\ \Rightarrow -\xi_L+U_R+U_C= U_{вх}

где:

\xi_L = -L \cdot \frac{dI}{dt}- ЭДС индукции на катушке, (направлено против изменения тока);

U_R=R \cdot I- падение напряжении на сопротивлении.

Поскольку в замкнутом контуре сила тока одинакова на всех элементах, перепишем уравнения, выразив силу тока через напряжение на конденсаторе. Сила тока в цепи равна изменению заряда конденсатора:

I =\frac{dq}{dt} где:

q=C\cdot U_C- заряд кондесатора.

Тогда сила тока в цепи связана с напряжение на конденсаторе соотношением:

I = C \cdot \frac{ dU_c}{dt}

После замены силы тока, ее выражением через U_Cполучим следующие выражение:

L \cdot C \cdot \frac{d^2U_c}{dt^2} +R\cdot C \cdot \frac{d U_c}{dt}+U_c = U_{вх}

Заменив U_C=y(t)и U_{ВХ} = x(t)получим уравнение колебательного звена:

\underbrace{L \cdot C}_{T_2^2} \cdot y''(t)+\underbrace{R \cdot C}_{T_1} \cdot y'(t) +y(t) =\underbrace{1 \cdot }_Kx(t)

Уравнение динамики звена описывается уравнением, аналогичным рассмотренном в предыдущем разделе (апериодическое звено второго порядка):   

T^2_2 \cdot y''(t)+T_1 \cdot y'(t)+ y(t) =K\cdot x(t) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.1)}

причем T_1<T_2, т.е. D= T_1^2-4 \cdot T_2^2 \leq 0

Учитывая, что D \leq0, удобнее представить уравнение динамики в другой форме, а именно:

Введем новые параметры: T\equiv T_2и \beta = \frac{T_1}{2 \cdot T_2}, где \beta - параметр (коэффициент) затухания (демпфирования).

Подставляя новые параметры в (3.5.1):

T^2 \cdot y''(t)+2 \cdot \beta \cdot T\cdot y'(t)+y(t) = K \cdot x(t) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.2)}

Уравнение 3.5.2 - наиболее удобная форма представления уравнения динамики. 

Перейдем к изображениям: x(t) \rightarrow X(s) и y(t) \rightarrow Y(s)уравнение динамики в изображениях Лапласа:

(T^2_2 \cdot s^2+2 \cdot \beta \cdot T \cdot s+1) \cdot Y(s)=K \cdot X(s)

Передаточная функции колебательного звена:

W(s) =\frac{Y(s)}{X(s)}= \frac{ K}{ T^2 \cdot s^2+2 \cdot \beta \cdot T \cdot s + 1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.3)}

Еще раз подчеркнем, что параметр (коэффициент) затухания (демпфирования) 0 \le \beta \le 1, причем при \beta > 1свойства колебательного звена совпадают с аналогичными свойствами соответствующего апериодического звена 2-го порядка, а при \beta = 0звено выражается в консервативное, в котором могут существовать незатухающие гармонические колебания.

Выражение для АФЧХ получается после подстановки в (3.5.3) значения s=i\cdot \omega:

W(i \cdot \omega)=\frac{K}{T^2 \cdot (i \cdot \omega)^2+2 \cdot \beta \cdot T \cdot i \cdot \omega+1}=\\= \frac{K}{(1-T^2\cdot \omega^2)+2 \cdot \beta \cdot T \cdot i \cdot \omega} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.4)}

Домножим числитель и знаменатель формулы 3.5.4 на компексно сопряженное выражения для знаменателя (1-T^2\cdot \omega^2) - 2 \cdot \beta \cdot T \cdot i \cdot \omega:

W(i \cdot \omega) = \frac{K(1-T^2\cdot \omega^2) - K \cdot 2 \cdot \beta \cdot T \cdot \omega \cdot i}{(1-T^2\cdot\omega^2)^2+4 \cdot \beta^2 \cdot T^2 \cdot \omega^2}

Выражения для вещественной и мнимой частей принимают вид:

u( \omega) = \frac{K(1-T^2\cdot \omega^2) }{(1-T^2\cdot\omega^2)^2+4 \cdot \beta^2 \cdot T^2 \cdot \omega^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.5)}v(\omega) = \frac{ - 2 \cdot K \cdot \beta \cdot T \cdot \omega }{(1-T^2\cdot\omega^2)^2+4 \cdot \beta^2 \cdot T^2 \ \cdot \omega^2} \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.6)}

Амплитуда АФЧХ

A(\omega) = \sqrt{u(\omega)^2+v(\omega)^2} =\sqrt{\frac{K^2 \left( (1-T^2\cdot \omega^2)+4\cdot K^2 \cdot \beta^2 \cdot T^2 \cdot \omega^2 \right)}{((1-T^2\cdot \omega^2)^2+4 \cdot \beta^2 \cdot T^2 \cdot \omega^2)^2}}A(\omega) = \frac{K }{\sqrt{(1-T^2\cdot \omega^2)^2+4 \cdot \beta^2 \cdot T^2 \cdot \omega^2}} \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.7)}

Сдвиг фазы

\varphi (\omega) = \left \{ \begin{gathered} -arctg \frac{2 \cdot \beta \cdot T \cdot \omega}{1- T^2 \cdot \omega^2}, \ если \ \omega \le \frac{1}{T}; \\ -\pi- arctg \frac{2 \cdot \beta \cdot T \cdot \omega}{1- T^2 \cdot \omega^2}, \ \ если \ \ \omega > \frac{1}{T}. \ \end{gathered} \right. \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.8)}

Анализ формул (3.5.5 ? 3.5.8) показывает, что:

\omega \rightarrow 0 \Rightarrow \left \{ \begin{gathered} u(\omega) \rightarrow K; \\ v(\omega) \rightarrow 0; \\ A(\omega) \rightarrow K; \\ \varphi(\omega) \rightarrow 0; \end{gathered} \right. \ \ \ \ \ \ \ \omega \rightarrow \infty \Rightarrow \left \{ \begin{gathered} u(\omega) \rightarrow 0; \\ v(\omega) \rightarrow 0; \\ A(\omega) \rightarrow 0; \\ \varphi(\omega) \rightarrow - \pi; \end{gathered} \right. \ \ \ \ \ \ \ \mathbf{(3.5.9)}

Одной из главных особенностей АФЧХ является возможность существования экстремума в зависимости A(?). Выполним исследование на экстремум:

\frac{dA(\omega)}{d\omega}=\frac{d}{d\omega} \left( \frac{K}{\sqrt{(1-T^2\cdot\omega^2)^2+4\cdot\beta^2\cdot T^2\cdot \omega^2}}\right)=0\frac{\frac{d}{d\omega}K\cdot\sqrt{(1-T^2\cdot\omega^2)^2+4\cdot\beta^2\cdot\omega^2}-K \cdot \frac{d}{d\omega}\sqrt{(1-T^2\cdot\omega^2)^2+4\cdot\beta^2\cdot\omega^2}}{(1-T^2\cdot\omega^2)^2+4\cdot\beta^2\cdot\omega^2} = \\ =\frac{-0.5\cdot K\cdot((1-T^2\cdot\omega^2)^2+4\cdot\beta^2\cdot\omega^2)^{-1.5}\cdot[2\cdot(1-T^2\cdot\omega^2)\cdot(-2)\cdot T^2\cdot \omega+8 \cdot \beta^2\cdot\omega]}{(1-T^2\cdot\omega^2)^2+4\cdot\beta^2\cdot\omega^2}

Очевидно что, для того, что бы выражение равнялось нулю необходиом равенство нлую следующего выражения:

-4\cdot(1-T^2\cdot \omega^2)\cdot T^2 \cdot \omega+8 \cdot \beta^2\cdot T^2 \cdot \omega = 0

Отсюда вырражение для экстермума:

\omega_m=\frac{1}{T}\sqrt{1-2\cdot \beta^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.10)}

Очевидно, что \omega_mсуществует если (1- 2 \cdot \beta^2)\ge 0 \Rightarrow \beta \le\frac{\sqrt2}{2}

Если \beta < \frac{\sqrt{2}}{2}, то заивисмость A(\omega)имеет экстремум.

Если \beta >\frac{\sqrt{2}}{2}, экстремума в заивсимости A(\omega)нет.

Вычислим максимальное значение A(\omega), под ставим выражение для \omega_m 3.5.10 в формулу 3.5.7, получим:

A(\omega_m) =\frac{K}{\sqrt{\left [1 -T^2 \frac{1}{T^2}(1-2\beta^2) \right ]^2+4\beta^2T^2\frac{1}{T^2}(1- 2\beta^2)}} \RightarrowA(\omega_m) = \frac{K}{2 \cdot\beta \sqrt(1- \beta^2)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.11)}

Анализ вышеприведенных соотношений показывает, что при \beta < \frac{\sqrt{2}}{2}график A(\omega)имеет горб, который при уменьшении \beta растет и при \beta \rightarrow 0 \ \ \ \ \ \ A(\omega) \rightarrow \infty, что означает разрыв в зависимости A(\omega).

 Частоту ?м будем отождествлять с тем значением частоты входного гармонического воздействия, при которой имеет место максимальное значение амплитуды выходного сигнала.

Поскольку \beta = \frac{T_1}{T_2}, то очевидна роль постоянных времени : 

T_2– ‘раскачивает’ колебания, а T_1? ‘демпфирует’ их. Рассмотрим соответствующие графики:

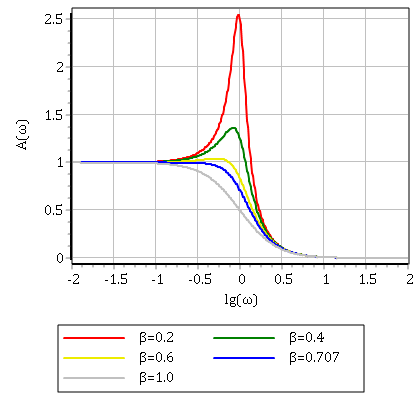
Рисунок 3.5.2 АЧХ колебательного звена
Рисунок 3.5.2 АЧХ колебательного звена
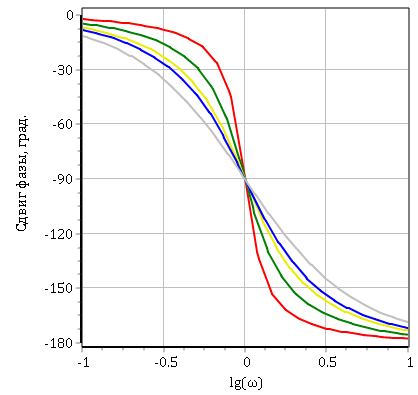
Рисунок 3.5.3 ФЧХ колебательного звена
Рисунок 3.5.3 ФЧХ колебательного звена

Данные графики аналогичны для случаев резонансов в теоретической механике, физике, электротехнике и т.д.

Величину \omega = \frac{1}{T} принято называть частотой свободных колебаний и обозначать ?0.

Рассмотрим колебательное звено в котором ? = 0. Очевидно, что в данном звене при ступечатом воздействии устанавливаются незатухающие колебания, а само звено вырождается в консервативное. При этом согласно формуле 3.5.10 выражение экстремума для такого звена:

\omega_m=\frac{1}{T}\sqrt{1-2\cdot 0^2} = \frac{1}{T}

Величину \omega = \frac{1}{T} принято называть частотой свободных колебаний и обозначать ?0.

Подставляя различные значения ? в формулу (3.5.5) или (3.5.6) построим годограф АФЧХ на комплексной плоскости:

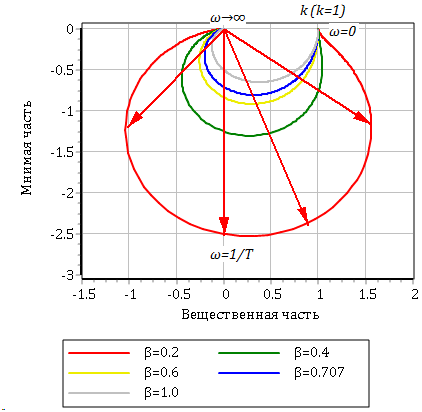
Рисунок 3.5.4 АФЧХ колебательного звена
Рисунок 3.5.4 АФЧХ колебательного звена
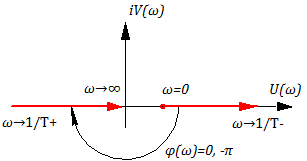
Рисунок 3.5.5 Годограф АФЧХ консервативного звена
Рисунок 3.5.5 Годограф АФЧХ консервативного звена

Построение ЛАХ ?Lm(?) не может быть сделано так же просто, как для предыдущих позиционных звеньев, т.е. она не сводится к комбинации отрезков прямых.

Будем использовать для построения графика ЛАХ нормированную (безразмерную) частоту \tilde{\omega} = \frac{\omega}{\omega_0}, где \omega_0 - частота свободных колебаний, имеющим место в консервативном звене со следующим уравнением динамики: 

T^2 \cdot y''(t)+y(t) = K \cdot x(t)

Решим данное уравнение динамики, используя корни характеристического уравнения L(\lambda )=0:

T^2\cdot \lambda^2+1=0 \Rightarrow \lambda_{1,2} = \pm i\cdot\frac{1}{T} = \pm i \cdot \omega_0y_{собств} = С_1\cdot e^{i \cdot \omega_0\cdot t}+C_2\cdot e^{-i\cdot \omega_0 \cdot t} \approx sin(\omega_0\cdot t)

На этом месте у меня всегда выносится мозг, как могут прыгающие на пружинке шарике, и электроны в электрическом контуре, описаны с помощью одиникового выражения, формулы синуса - соотношения стороно в прямоугольном треуголнике. Как это работает?!

Введя новую переменную \tilde{\omega}в выражение для Lm(?) = 20 lg (А(?)):

Lm(\omega) =20\cdot lg(K) - 20 \cdot lg(\sqrt{(1-T^2\cdot \omega^2)^2+4 \cdot \beta^2\cdot T^2\cdot \omega^2}) = =20\cdot lg(K) - 20 \cdot lg(\sqrt{\left (1-\frac{\omega^2}{\omega_0^2} \right)^2+4 \cdot \beta^2\cdot \frac{\omega_2}{\omega_0^2}} \RightarrowLm(\omega) =20\cdot lg(K) - 20 \cdot lg(\sqrt{\left (1-\tilde{\omega}^2 \right)^2+4 \cdot \beta^2\cdot \tilde {\omega}^2} \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.12)}

Таким образом мы получаем выражение, которое не зависит от Т. Такая форма представления позволяет ‘свести’ различные ЛАХ при различных Т   к автомодельному (‘универсальному’) виду графиков.

На рисунке ниже представлен график Lm(?) в форме (3.5.12), построенный фактически в логарифмических координатах, причем коэффициент усиления K=1. 

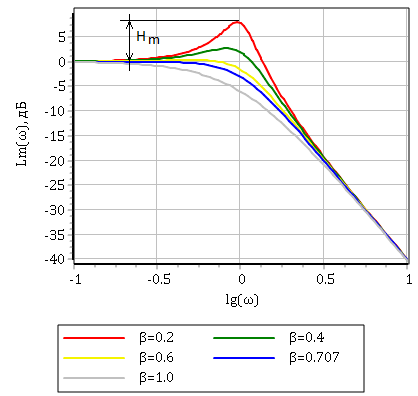
Рисунок 3.5.6 ЛАХ колебательного звена
Рисунок 3.5.6 ЛАХ колебательного звена

Подчеркнем, что при такой форме представления все ЛАХ при различных T1и T2 можно “собирать вместе”.

 Величина Hm (см. рис. 3.5.6) называется превышением:

H_m=20\cdot lg \frac{1}{2\cdot\beta\cdot \sqrt{1-\beta^2}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.13)}

Если , \beta <<1, \ \ \beta \approx 0 то в упрощенных расчетах величину превышения Hm можно оценить, как:

H_m = 20 \cdot lg \frac{1}{2\cdot \beta}=-20lg(2\cdot \beta) \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.14)}

при ?=?m (эта формула работает для ярко выраженных горбов).

Вычислим переходную функцию звена h(t):

h(t)= L^{-1}[H(s)] =L^{-1}\left[\frac{W(s)}{s}\right] = L^{-1}\left[ \frac{K}{s(T^2\cdot s^2+2 \cdot \beta \cdot s+1)} \right] \Rightarrowh(t) =\frac{K}{T^2}L^{-1} \left[ \frac{1}{s(s^2+\frac{2\cdot \beta}{T}\cdot s)+\frac{1}{T^2}} \right]

Для вычисления переходной функции воспользуемся формулой Хэвисайда сначала найдем полюса s_1,s_2,s_3:

s \cdot \left(s^2+\frac{2 \cdot \beta}{T}+ \frac{1}{T^2} \right) =0 \Rightarrow \\ s_1 =0;\\s_2 = -\frac{\beta}{T}+i \cdot \frac{1}{T}\sqrt{1- \beta^2} \\s_3 = -\frac{\beta}{T}-i \cdot \frac{1}{T}\sqrt{1- \beta^2}

По формуле Хэвисайда

h(t)= \frac{K}{T^2} \sum_1^3 \lim_{s \to s_j } \left[ \frac{(s-s_j)}{s \cdot(s^2+\frac{2 \cdot \beta}{T}\cdot s+\frac{1}{T^2})} \cdot e^{st} \right]\ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.15)}

Разберем отдельно каждый предел:

\lim_{s \to 0} \left [ \frac{(s-0)}{s \cdot(s^2+\frac{2 \cdot \beta}{T}\cdot s+ \frac{1}{T^2})} \cdot e^{st}\right]=\frac{1}{0+0+\frac{1}{T^2}}\cdot1=T^2

Для вычисления 2-го и 3-го предела в формуле Хэвисайда более удобно использовать новые переменные m и n:

m=-\frac{\beta}{T}; \ \ \ \ \ \ \ n = \frac{1}{T}\sqrt{1-\beta^2}

Тогда корни s_1, s_2выраженные через переменные m и n будут записаны как:

s_2 =m+i\cdot n; \ \ \ \ \ \ \ \ s_3=m-i\cdot n

Разложим квадратный трех член в скобках в занаментели на множетели и использованием корней s_2, s_3:

s^2+\frac{2\cdot\beta}{T} \cdot s+\frac{1}{T^2} =(s-s_2)\cdot(s-s_3)

тогда 2-й предел в фомуле Хевисайда можно записать как:

\lim_{s \to (m+i \cdot n)} \left [ \frac{s -m-i\cdot n}{s (s - m-i\cdot n)(s-m+i \cdot n)} \cdot e^{s\cdot t}\right] =\\ = \frac{1}{(m+i\cdot n)(m+i\cdot n-m+i \cdot n)} \cdot e^{(m+i \cdot n)\cdot t} = \\ = \frac{1}{(m +i\cdot n)\cdot 2 \cdot i\cdot n} \cdot e^{m\cdot t}\cdot e^{i\cdot n\cdot t}

домножая на комплексно сопряженное число (m-i \cdot n)\cdot i числитель и знаменатель получим значение второго предела:

-\frac{n+m \cdot i}{(m^2+n^2)\cdot 2 \cdot n}\cdot e^{m\cdot t}\cdot e^{i\cdot n \cdot t }

Анологично 3-й предел в формуле Хевисайда можно записать как:

\lim_{s \to (m-i \cdot n)} \left [ \frac{s -m+i\cdot n}{s (s - m-i\cdot n)(s-m+i \cdot n)} \cdot e^{s\cdot t}\right] =\\ = \frac{1}{(m-i\cdot n)(m-i\cdot n-m-i \cdot n)} \cdot e^{(m-i \cdot n)\cdot t} = \\ = -\frac{1}{(m -i\cdot n)\cdot (-2) \cdot i\cdot n} \cdot e^{m\cdot t}\cdot e^{i\cdot n\cdot t}

домножая на комплексно сопряженное число (m+i \cdot n)\cdot i, числитель и знаменатель получим значение третьего предела:

\frac{-n+m\cdot i}{(m^2+n^2)\cdot 2\cdot n}e^{m\cdot t}\cdot e^{-i\cdot n\cdot t}

Отдельно сложим второе и третье слогаемое в формуле Хевисайда:

\sum_2^3 =-\frac{e^{m\cdot t}}{2 \cdot n \cdot (m^2+n^2)} \left [ (n+i \cdot m)\cdot e^{i \cdot n \cdot t}+(n-i \cdot m)\cdot e^{-i \cdot n \cdot t} \right ]==-\frac{e^{m\cdot t}}{2 \cdot n \cdot(m^2+n^2)}\left[ n \cdot e^{i \cdot n \cdot t} +i \cdot m \cdot e^{i \cdot n \cdot t}+n \cdot e^{-i \cdot n \cdot t}-i \cdot m \cdot e^{-i \cdot n \cdot t} \right] == -\frac{e^{m \cdot t}}{2 \cdot n \cdot (m^2+n^2)} \left [ n\cdot(\underbrace{e^{i \cdot n \cdot t}+ e^{-i\cdot n \cdot t}}_{2 \cdot cos(n \cdot t)})+ i \cdot m \cdot(\underbrace{e^{i \cdot n \cdot t}-e^{-i \cdot n \cdot t}}_{2\cdot i \cdot sin(n \cdot t)})\right ]== -\frac{e^{m \cdot t}}{2 \cdot n \cdot(m^2+n^2)}\left [n \cdot cos (n \cdot t)- m \cdot sin(n \cdot t)\right ] == -\frac{e^{m \cdot t}}{2 \cdot n \cdot(m^2+n^2)}\left [cos (n \cdot t)- \frac{m}{n} \cdot sin(n \cdot t)\right ]

подставляя значения n и m:

(m^2+n^2)=\frac{\beta^2}{T^2}+\frac{1-\beta^2}{T^2}=\frac{1}{T^2}\\ \frac{m}{n}=-\frac{\beta}{T}\cdot \frac{T}{\sqrt{1-\beta^2}}

и собирая все слагаемые формулы 3.5.15 получаем:

h(t)=\frac{K}{T^2}\left [T^2 - T^2 \cdot e^{m \cdot t} (cos(n \cdot t)+\frac{\beta}{\sqrt{1-\beta^2}}\cdot sin(n \cdot t)) \right] \Rightarrow h(t) = K \left [ 1 -e^{-\frac{\beta}{T}\cdot t} \left(cos \frac{\sqrt{1-\beta^2}}{T}\cdot t+\frac{\beta}{\sqrt{1-\beta^2}}sin\frac{\sqrt{1-\beta^2}}{T} \cdot t \right) \right ] \ \ \ \ \ \mathbf{(3.5.16)}

Введем новую переменную \omega_c = \frac{1}{T}\sqrt{1-\beta^2}и перепишем формулу для переходной функции:

h(t) = K \left [1 -e^{-\frac{\beta}{T} \cdot t} \left( cos(\omega_c \cdot t)+\frac{\beta}{\sqrt{1 -\beta^2}}sin(\omega_c \cdot t)\right) \right ] \ \ \ \ \ \ \ \mathbf{(3.5.16.a)}

Величина \omega_c = \frac{1}{T}\sqrt{1-\beta^2}называется частотой собственной колебаний при 0<\beta< 1.

Таким образом в описании колебательного звена появилось три “новых” частоты \omega_m < \omega_m <\omega_c

  • \omega_0 - частота свободных колебаний;

  • \omega_m- частота, соответствующая максимальной амплитуде;

  • \omega_c- частота собственных колебаний.

Причем \omega_m < \omega_m <\omega_c

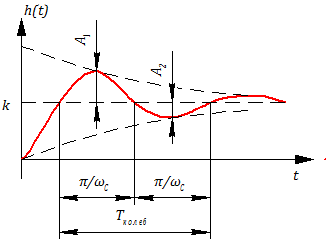
Рассмотрим предельные случаи для ? (т.е. ? = 1 и ? = 0):

Если \beta \to 0, то \omega_c \to \omega_0=\frac{1}{T}:

h(t) = K \left [1 -e^{0\cdot t} \left ( cos \frac{t}{T} +0 \cdot sin \frac{t}{T} \right ) \right]h(t) = K \left [ 1 - cos \frac{t}{T}\right ] \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.17)}

3.5.17 - переходная функция консервативного звена.

Рисунок 3.5.6 Переходная функция консервативного звена
Рисунок 3.5.6 Переходная функция консервативного звена

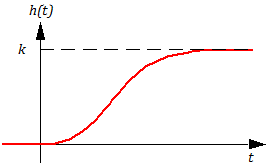
Если \beta \to 1, то \omega_c \to 0, т.е. собственных колебаний в звене нет, процесс без колебательный. В этом случае возникают трудности со вторым слагаемым в круглых скобках формулы (3.5.16).

Раскрываем неопределенность типа \frac{0}{0}:

\lim_{\beta \to 1 } \left[ \frac{\beta}{\sqrt{1-\beta^2}} \cdot sin \left (\frac{\sqrt{1-\beta^2}}{T} \cdot t \right ) \right ] = \lim_{\beta \to 1} \left [ \frac{\beta \cdot t}{T} \cdot \frac{sin(\frac{\sqrt{1-\beta^2}}{T}\cdot t)}{\underbrace{\frac{\sqrt{1-\beta^2}}{T}}_{\approx \frac{sin x}{x}}} \right ]=\frac{t}{T}h(t)_{\beta=1} = K \left [ 1 - e^{-\frac{t}{T}}\cdot \left (1 +\frac{t}{T} \right)\right] \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.18)}

эта формула соответствует также аналогичной формуле для апериодического звена 2-го порядка при D = 0 (совпадающие полюса).        

Рисунок 3.5.8 Переходная функция колебательного звена (при ? = 1)
Рисунок 3.5.8 Переходная функция колебательного звена (при ? = 1)
Рисунок 3.5.9 Переходная функция колебательного звена (при 0 < ? < 1)
Рисунок 3.5.9 Переходная функция колебательного звена (при 0 < ? < 1)

Если 0<\beta<1, то \beta =T\cdot \frac{\omega_c}{\pi} \cdot \ln \frac{A_1}{A_2}

Дифференцируя во времени формулы (3.5.16 ? 3.5.18), найдем соответствующие весовые функции для крайних значений \beta(w(t)): 

Если \beta =0 \Rightarrow

w(h)_{\beta =0} = h'(t)= \frac{K}{T} sin \left ( \frac{t}{T} \right ) \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.19)}
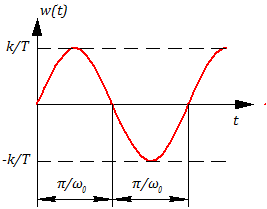
Рисунок 3.5.10 Весовая функция колебательного звена при ? = 0.
Рисунок 3.5.10 Весовая функция колебательного звена при ? = 0.

Если \beta =1 \Rightarrow

w(h)_{\beta =1} = h'(t)= K \left [ \frac{1}{T} \cdot e^{-\frac{t}{T}}\cdot \left( 1+ \frac{t}{T} \right) - e^{-\frac{t}{T}} \cdot \frac{t}{T} \right ]w(h)_{\beta =1} = \frac{K}{T^2} \cdot t \cdot e ^{-\frac{t}{T}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.20)}
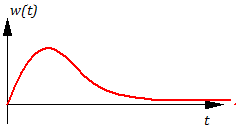
Рисунок 3.5.11 Весовая функция колебательного звена при ? = 1.
Рисунок 3.5.11 Весовая функция колебательного звена при ? = 1.

Если 0<\beta <1 \Rightarrow

w(t) = h'(t) = \frac{K}{T\cdot \sqrt{1 -\beta^2}}\cdot e^{-\frac{\beta \cdot t}{T}} \sin \left ( \frac{\sqrt{1-\beta^2}}{T} \cdot t \right) \ \ \ \ \ \ \ \ \ \ \mathbf{(3.5.21)}\beta = T\cdot \frac{\omega_c}{\pi}\cdot \ln\frac{B_1}{B_2}
Рисунок 3.5.12 Весовая функция колебательного звена при 0 < ? < 1.
Рисунок 3.5.12 Весовая функция колебательного звена при 0 < ? < 1.

Примерами колебательного звена можно считать:

  1. R ? C ? L – цепь см. начало статьи; 

  2. Упругие механические передачи;

  3. Гироскопический “маятник”;

  4. Управляемый двигатель постоянного тока (при некоторых условиях).

Пример

В качестве примера для исследования колебательного звена возьмем электрический колебательный контур, который был рассмотрен в начале статьи и сравним его с моделью колебательного звена. Модель контура представлена на рисунке 3.5.13:

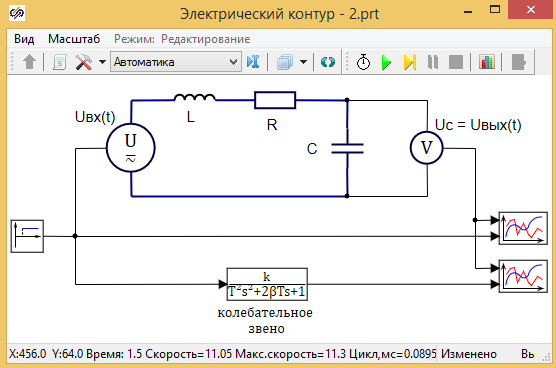
Рисунок 3.5.13 Модель колебательного контура
Рисунок 3.5.13 Модель колебательного контура

Схема модели содержит в себе:

  1.   модель электрического контура в виде электрической схемы;

  2.    модель контура в виде колебательного звена. 

Параметры электрической схемы задаются в виде общих сигналов проекта. См. рис. 3.5.14:

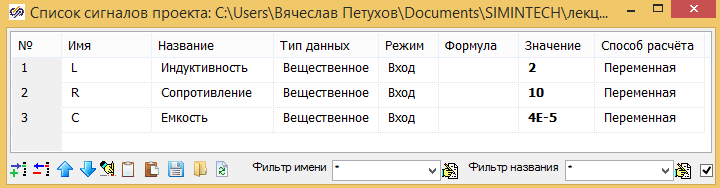
Рисунок 3.5.14 Общие сигналы проекта.
Рисунок 3.5.14 Общие сигналы проекта.
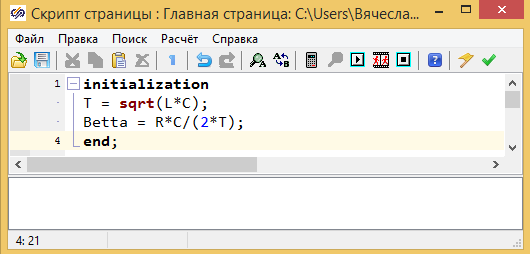
Рисунок 3.5.15. Вычисление параметров для колебательного звена.
Рисунок 3.5.15. Вычисление параметров для колебательного звена.

В общем скрипте проекта выполняется вычисление постоянной времени T и коэффициента демпфирования \beta

Для сравнения модели в виде электрической схемы и модели в виде колебательного звена, выполним моделирование ступенчатого возрастания напряжения, с 0 до 1 В.

Рисунок 3.5.16. Графики напряжений источника и на конденсаторе.
Рисунок 3.5.16. Графики напряжений источника и на конденсаторе.

Выполним гармонический анализ данной модели, аналогично тому, как мы это делали для модели демпфера и камеры смешения реактора демпфера.

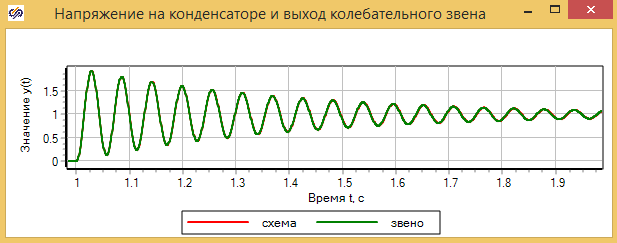
Рисунок 3.5.17 Сравнение модели контура и колебательного звена
Рисунок 3.5.17 Сравнение модели контура и колебательного звена

На графике рис. 3.5.16 видно возникновение колебательного процесса и его затухание с течением времени. График на рис. 3.5.17 показывает практически полное совпадение модели в виде электрической схемы и модели в виде колебательного звена:

Выполним гармонический анализ данной модели, аналогично тому, как мы это делали для модели демпфера и камеры смешения реактора демпфера (см. разделы 3.3 Апериодическое звено 1-го порядка. и 3.1 Амплитудно-фазовая частотная характеристика). Расчетная схема для такого анализа приведена на рисунке 3.5.18.

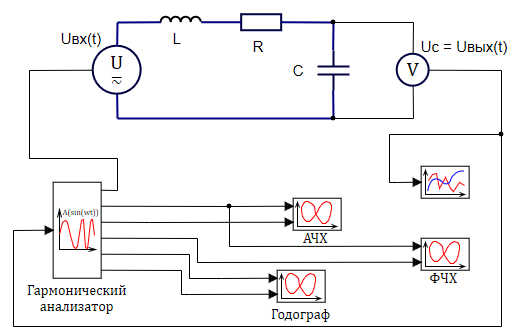
Рисунок 3.5.18. Частотный анализ электрического контура
Рисунок 3.5.18. Частотный анализ электрического контура

Амплитуда входного тестового сигнала - 1 В, аналогична амплитуде ступенчатого воздействия из предыдущего численного эксперимента.

Результаты анализа представлены на рисунке 3.5.19

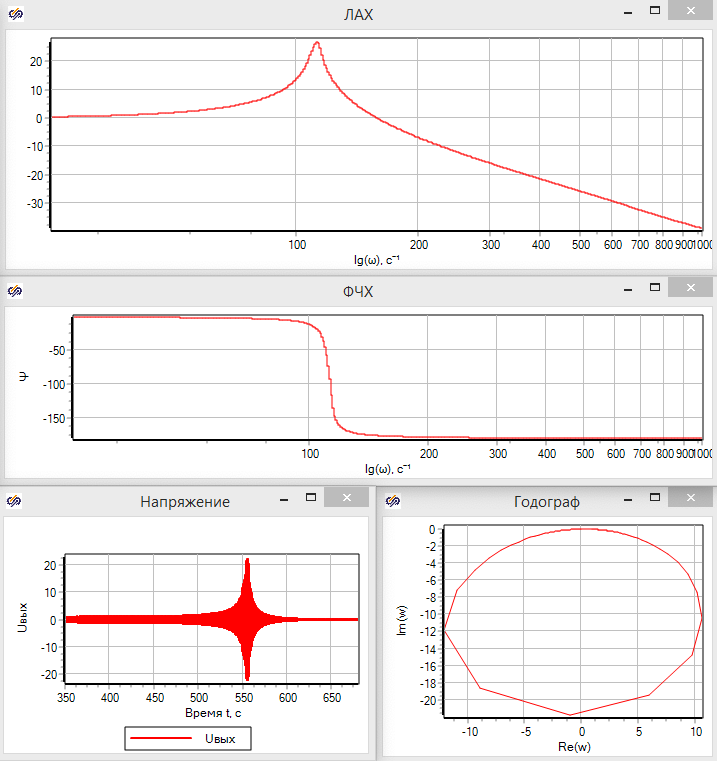
Рисунок 3.5.19 Результаты гармонического анализа.
Рисунок 3.5.19 Результаты гармонического анализа.

Результаты моделирования показывают практическое совпадение теоретических значений частоты, при которой достигается максимальная амплитуда сигнала, и значений, полученных в результате моделирования электрической схемы: Теоретическое значение = 111,75 Гц Полученное моделированием = 112,2 Гц

Для исследования влияния параметров модели добавим на схему управляющие элементы, которые буду менять сопротивление резистора и емкость конденсатора во время расчёта.

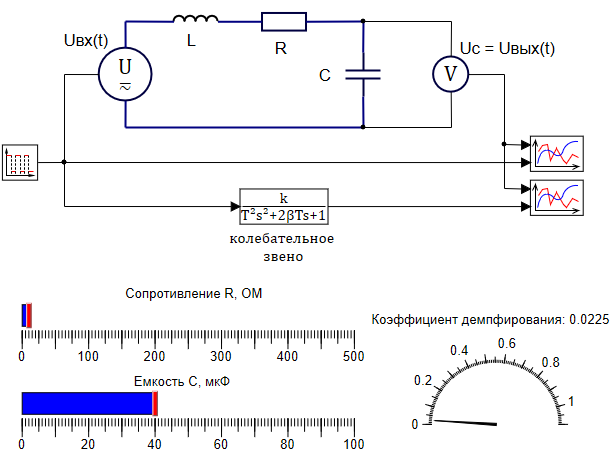
Рисунок 3.5.20 Модель с изменяемыми параметрами контура.
Рисунок 3.5.20 Модель с изменяемыми параметрами контура.

Также выведем на схему значения коэффициента демпфирования с помощью текста и стрелочного прибора. Чтобы можно было отслеживать влияние параметров цепи на процесс, заменим ступенчатое воздействие на меандр. Схема модели примет вид, как это представлено на рисунке 3.5.20

Чтобы данная конфигурация заработала, необходимо добавить в скрипт программы код, который заберёт значения с ползунков и передаст их в параметры модели (см. рис 3.5.21)

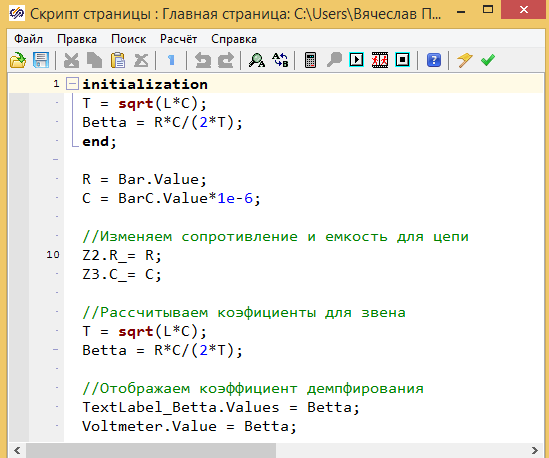
Рисунок 3.5.21. Скрипт изменения параметров модели
Рисунок 3.5.21. Скрипт изменения параметров модели

Данная модель позволяет изменить сопротивление резистора и емкость конденсатора, и оценить влияние этого изменения на переходной процесс. Подобное изменение мы делали в предыдущем примере, где изменение силы терпения в механическом демпфере выполнялось автоматически, и апериодическое звено второго порядка превращалось в колебательное. В текущем примере мы можем «вручную», с помощью ползунков, изменить параметры цепи и получить из колебательного звена апериодическое звено второго порядка.

Например, при положении ползунков, изображенном на рисунке 3.5.22, колебательный контур превращается в апериодическое звено второго порядка (см. рис. 3.5.23.)

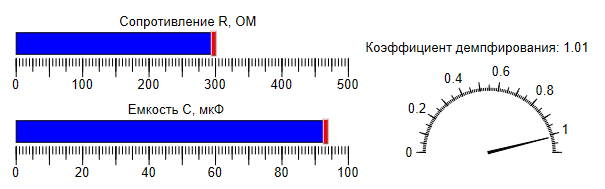
Рисунок 3.5.22. Настройки контура для устранения колебаний
Рисунок 3.5.22. Настройки контура для устранения колебаний
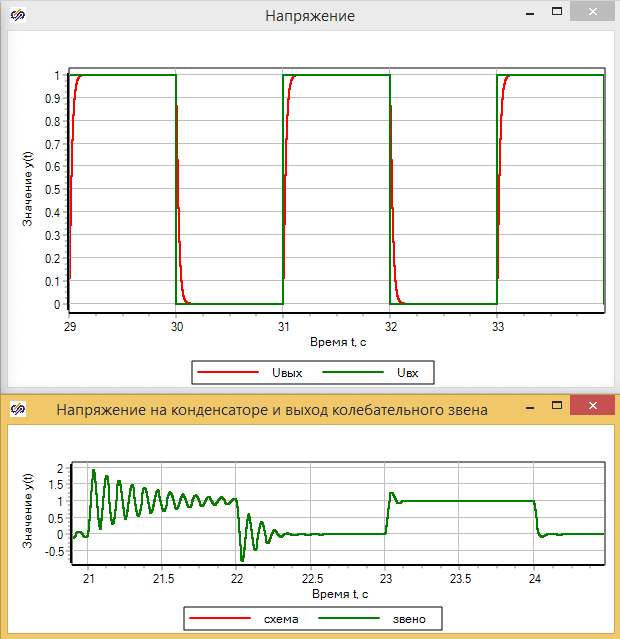
Рисунок 3.5.23. Графики изменения переходных процессов в контуре при изменении R и С.
Рисунок 3.5.23. Графики изменения переходных процессов в контуре при изменении R и С.

При увеличении сопротивления резистора и емкости кондесатора происходит увеличение коэффициента демпфирования, и когда Если \beta >1 \Rightarrow колебательное звено превращается в апериодическое 2-го порядка. (см. график на рис 3.5.23.

Поскольку мы рассматриваем общую тему частотных характеристик, доработаем наш виртуальный стенд с контуром так, чтобы можно было «вручную» исследовать частотные воздействия на контур.

Заменим в качестве источника блок «меандр», на блок «синусоида» и добавим ползунок, изменяющий частоту этого источника, а также добавим на схему текстовые надписи, отображающие частоты максимальной амплитуды, частоты собственных колебаний и частоты свободных колебаний. Расчетная схема будет выглядеть как на рисунке 3.5.25

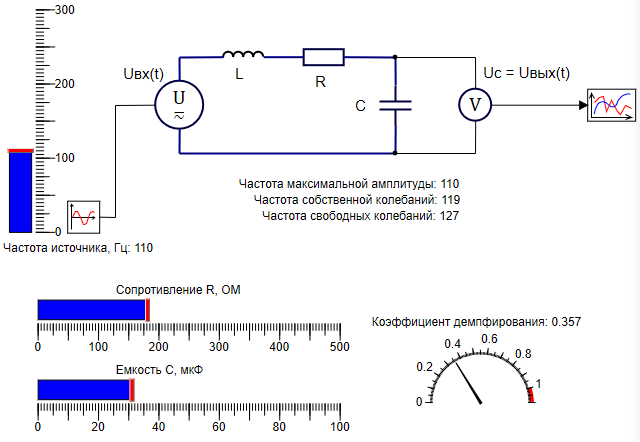
Рисунок 3.5.24 Схема колебательного контура с настройками частоты источника.
Рисунок 3.5.24 Схема колебательного контура с настройками частоты источника.

Добавляем в скрипт необходимый код, обеспечивающий расчет частот максимальной амплитуды, собственных колебаний и свободных колебаний, а также код для изменения частоты источника напряжения. Данный код скрипта приведен на рисунке 3.5.25

Рисунок 3.5.24 Скрипт для управления и отображения частоты.
Рисунок 3.5.24 Скрипт для управления и отображения частоты.

Данная модель позволяет независимо настраивать параметры цепи и частоту источника напряжения.

В частности, можно убедится, что при различных настройках колебательного контура максимальная амплитуда колебаний напряжения достигается тогда, когда частота источника совпадает с частотой максимальной амплитуды, рассчитанной по формуле 3.5.10 см.скрипт на рис. 3.5.24.

Видео с управлением данным контуром можно посмотреть по ссылке.

А, например, на следующем графике изображено изменение напряжения на конденсаторе при повышении частоты источника от 0 до 300 Гц с шагом 1 Гц – 1 сек.

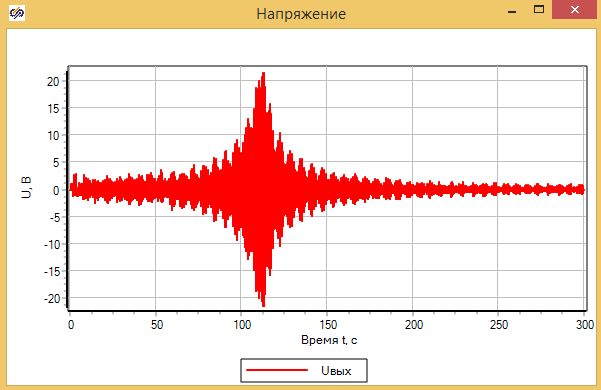
График построен путем давления в скрипте строки, передвигающей ползунок каждую секунду на 1 единицу (Гц) BarW.Value=Round(time) .

Как видим результат ручного управления совпал с результатом гармонического анализа максиму амплитуды теоретической частоте максимума - 112 Гц.

Примеры проектов для самостоятельного изучения можно взять по ссылке здесь.

Предыдущая лекция. 3.4 Апериодическое звено 2?го порядка.