Многим известна проблема трёхмерной графики — отсутствие легковесных кроссплатформенных решений в вопросе вывода текста.
Большинство реализаций позволяет использовать выбранный шрифт в виде текстуры. Публикуемая библиотека ttf2mesh реализует другой способ — она преобразует векторные символы TrueType шрифта в сеточные объекты. Это позволяет выводить текст в виде набора треугольников.
Такой подход имеет как важные преимущества, так и недостатки. Сложность описываемой далее задачи и созерцание великолепных форм шрифтового дизайна доставили массу удовольствия при разработке. Надеюсь, и Вам понравится.
Погружение в проблему
На сайте stackoverflow можно встретить вопрос "How to draw text using only OpenGL methods?". Развёрнутый ответ к нему, начинается с фразы "Why it is hard". Дам краткий перевод этого ответа, поскольку лучше — едва ли получится описать проблему.
Распространённые шрифты (такие как TrueType или OpenType) имеют векторный формат представления символов: их очертание задаётся набором кривых Безье.
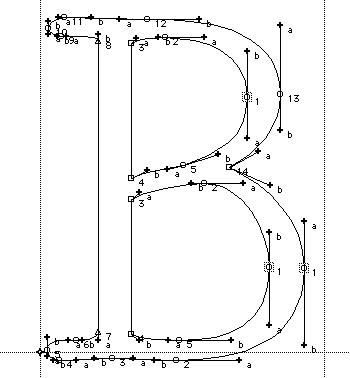
Растеризация данных в таком формате — достаточно специфическая задача и выходит за рамки OpenGL, который привык оперировать с примитивами меньшей сложности (точки, прямые, треугольники).
Поэтому, простым способом признаётся растеризация шрифта на CPU, а затем — передача символов OpenGL-у в виде текстуры. Вместо множества текстур малого размера принято использовать одну текстуру, содержащую всё множество нужных символов. Такой подход иногда называют текстурным атласом:

Подготовить такой атлас непросто, учитывая попытку наиболее плотным образом разместить символьные глифы в родительском прямоугольнике. Также указывается, что подобная техника используется в web-дизайне (CSS-sprites).
На конференции FOSDEM 2014, отмечает автор ответа, рассматривались и другие существующие техники:
- Тесселяция: преобразуем символы шрифта в набор треугольников. Последние GPU хорошо умеет выводить. Недостатки: формируется много треугольников; процесс имеет сложность O(N log N).
- Вычислять кривые на шейдерах. Недостатки: сложно, см. Resolution independent cubic bezier drawing on GPU (Blinn/Loop)
- Прямая аппаратная реализация вроде OpenVG. Недостатки: API не получил единой, широко распространённой реализации (см. OpenGL, OpenVG. Draw text и OpenVG implementation)
Автор ответа рассказывает, что отображение 3d-текста в перспективной проекции тоже является объектом исследований на момент Марта 2016 года. Самой популярной техникой в этой области является т.н. "Distance fields" (техника работы с растром, см. на Хабре). Далее рассказывается об известных реализациях.
Решения на базе FreeType
Библиотека FreeType для растеризации шрифтов имеет открытый исходный код и большую популярность. По этой причине также получила популярность библиотека FTGL, которая предоставляет удобный API, позволяет формировать текстурные атласы и использует "Distance fields" из коробки.
Другая известная библиотека — libgdx.
Решения на базе других растеризаторов
github.com/nothings/stb/blob/master/stb_truetype.h
www.angelcode.com/products/bmfont
Далее автор ответа приводит разные библиотеки, позволяющие вывести текст с использованием растеризированного шрифта. Отличия реализаций заключаются в форматах текстур (DDS, PNG) и привлекаемых растеризаторах. Детально останавливаться на этом не станем — советую изучить оригинальный топик.
Рассмотрим указанные на FOSDEM 2014 недостатки тесселяции.
Формируется много треугольников
Сразу напрашивается вопрос: а много — это сколько? Следующее изображение имеет в полном тексте с хорошим качеством 6000 треугольников (проверено на шрифте Ubuntu без засечек):

Шрифт с засечками даст в 2.5 раза больше треугольников (Times New Roman с засечками, 15000 треугольников).
Много ли это, учитывая, что современные игры в сцене содержат на порядок больше треугольников (а иногда и на два)? Учитывая потенциал оптимизации (выключение источников, текстур, теста глубины, работа с памятью GPU и прочее), такое количество треугольников на мой взгляд не выглядит критическим.
Сложность O(N log N)
Данная сложность, без сомнений, взята из анализа алгоритмов триангуляции. Вкратце, триангуляция (далее мы будем использовать этот термин) — это то же что тесселяция при замощении фигуры треугольниками. Множитель log(N) затруднительно считать определяющим. Кроме того, он часто нивелируется алгоритмически. Так, например, в книге А.В. Скворцова "Триангуляция Делоне и её применение" указывается, что не смотря на то что некоторые алгоритмы имеют предельную сложность , их средняя производительность всё же стремится к . Далее будет описан алгоритм линейного заметания, применяемая модификация которого незначительно отличается по сложности от .
С учётом сказанного, сеточные шрифты на практике выглядят привлекательно. Они способны решить сразу несколько проблем, присущих текстурным шрифтам:
- Сеточные шрифты масштабируемы
- Не нужно хранить объёмные растры для разных шрифтов и их размеров
- Решается проблема перспективной визуализации
- Множество приложений могут обходиться в принципе без текстур
- Сеточные шрифты применимы в других областях (например, в 3d-печати)
К недостаткам сеточных шрифтов можно отнести: при выводе на экран обязателен антиалиасинг; число треугольников на некоторых курсивных шрифтах и шрифтах с засечками может показаться большим для мобильных приложений.
Что же. Взвесив все "за" и "против", приступим к описанию того что получилось.
Описание библиотеки ttf2mesh
Дизайн сделан под влиянием концепции "не виляй собакой". Поэтому ttf2mesh — это всего два файла (ttf2mesh.h и ttf2mesh.c) написанных в стандарте C99. Основные и обычно попарно вызываемые функции, это:
| Выделение памяти | Освобождение памяти |
|---|---|
| ttf_list_fonts и ttf_list_system_fonts | ttf_free_list |
| ttf_load_from_file и ttf_load_from_mem | ttf_free |
| ttf_glyph2mesh | ttf_free_mesh |
Не буду останавливаться на описании API. Оно небольшое, а в ttf2mesh.h присутствуют doxygen-комментарии. Добавлю только что есть ещё функция ttf_export_to_obj, позволяющая экспортировать весь шрифт в файл формата Wavefront .obj. Это будет интересно тем, кто решит попробовать использовать сеточный шрифт. Для этих целей в папке examples репозитория лежит приложение-конвертер под названием ttf2obj.
Процесс преобразования можно разбить на следующие этапы:
- Чтение TTF-файла шрифта и всего набора векторных глифов, содержащегося в нём
- Линеаризация контуров (подготовка ломаных из набора гладких кривых)
- Исправление контурных ошибок
- Определение контурной иерархии
- Триангуляция с ограничениями в несколько этапов
5.1. Выпуклая триангуляция
5.2. Добавление ограничений (вставка структурных отрезков)
5.3. Удаление лишних треугольников
5.4. Оптимизация Делоне - Подготовка сетки
Чтение TTF-файла
Полное описание формата файла есть на сайте Microsoft (OpenType specification). OpenType-шрифт (.otf) — это развитый TrueType-шрифт (.ttf), с той же базовой структурой файла, но имеющий некоторые дополнения. Забегая вперёд, скажу, что библиотека пока что поддерживает только TTF, но в скором времени поддержка будет расширена на такие форматы, как OTF и TTC.
В двух словах о формате. При продуманной файловой структуре (деление на таблицы похоже на ELF файлы) TrueType формат отличается одной неприятной особенностью… В попытке уменьшить размер файла разработчики заложили великое многообразие вариантов кодирования одной и той же сущности. Эти варианты переключаются в зависимости от разных бит в разных словах… Возможно, на тот момент авторы посчитали, что полноценная компрессия известными методами будет затратной.
Парсер TTF-файлов был успешно протестирован на наборе Windows 7 font list и на наборе шрифтов Ubuntu 18.04.4 LTS (в общей сумме более 500 TTF файлов).
Если тема структуры TrueType шрифтов будет интересна читателю — подготовлю отдельную статью. Пока что продолжим.
Линеаризация контуров
Гладкая кривая — это прекрасно, но сетку можно построить только если её разбить на отрезки. На следующем рисунке показано как влияет введённый параметр outline quality на визуальное качество изображения.
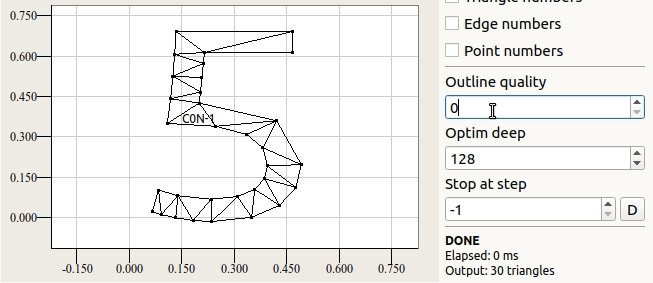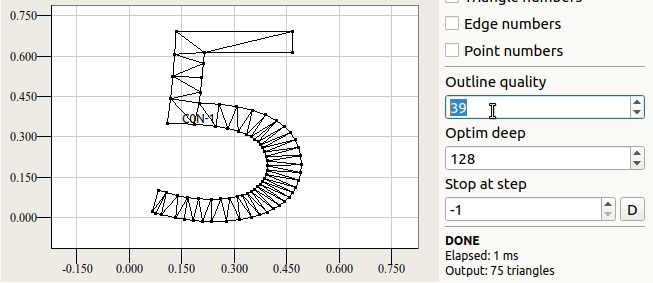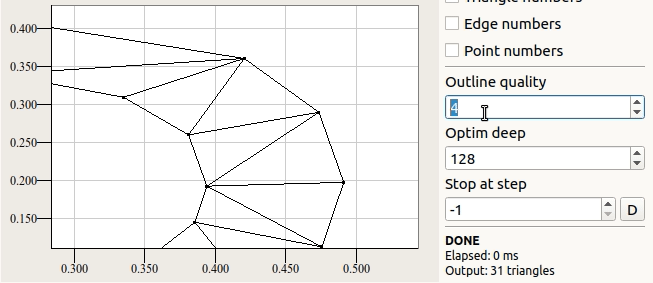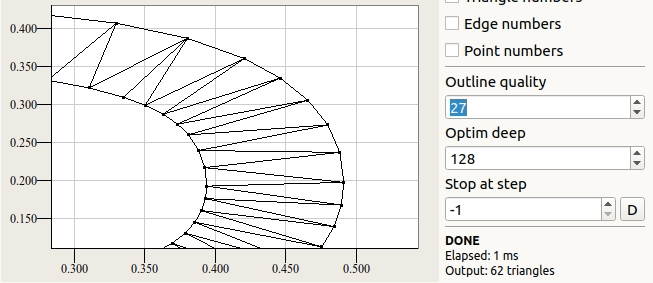
Данный параметр численно определяет на какое количество секторов требуется разбить окружность чтобы та не выглядела ребристой.
Каждый раз при подготовке сетки в ttf2mesh требуется указывать этот параметр. При этом предлагается пользоваться определениями TTF_QUALITY_LOW, TTF_QUALITY_NORMAL и TTF_QUALITY_HIGH. Низкий уровень детализации хорош при выводе в маленьком масштабе. При нормальном уровне дефекты фактически не прослеживаются на разных масштабах.

При выводе "Q" на обозначенных уровнях детализации формируется 76, 97 и 175 треугольников.
Исправление контурных ошибок
Поскольку дизайнеров уже похвалил, пришла пора их поругать. Тем более есть за что — они допускают определённые ошибки при дизайне шрифтов. Эти ошибки заключаются в допущении разного рода контурных дефектов. При растеризации контурные дефекты либо не проявляются, либо видны при значительном увеличении. Ввиду специфики процесса триангуляции эти дефекты могут приводить к неудаче при построении сетки. Обнаруживаются следующие ошибки:
- Дублирующиеся контуры
- Самопересечение контура
- Пересечения разных контуров
Рассмотрим эти случаи.
Дублирующиеся контуры наблюдаются в нескольких шрифтах, в частности, на символе U+2592 (-). Это такая шашечка такси на много квадратиков. Очевидно, что можно нарисовать в редакторе несколько квадратиков, а потом их размножить по Ctrl+V. Ну и ничего если несколько квадратиков спряталось точно друг под другом… Триангуляция такие шутки не прощает: если в граф попадает две вершины с одинаковыми координатами, то задача вырождается.
Кроме дублирующихся контуров встречаются и просто дублирующиеся узловые точки, но они библиотекой исключаются из рассмотрения путём либо удаления (если соседние), либо раздвижения контуров на EPSILON.
Самопересечение контура — самый неприятный контурный дефект.
Чаще всего случаются перекруты. Это когда на очень небольшой площади глифа натыкано великое множество опорных точек, в результате чего кривая Безье бьётся в конвульсиях и пересекает саму себя несколько раз. Растеризатор это отрабатывает несколько раз проинвертировав цвет соответствующего пикселя, а поскольку этот пиксель лежит где-то в районе антиалиасинга, наблюдатель дефект не замечает. Чаще всего такое наблюдается рядом с первой точкой контура. Догадываетесь почему?
Пересечения разных контуров — ещё один вид дефекта.
Существование этого вида дефекта получается объяснить только существованием лени дизайнера и пособничеством в этом компании Microsoft и Apple. Пример ленивого дизайна приводится ниже. Что же касается последних, Microsoft и Apple допускают пересекающиеся и самопересекающиеся контуры (см. Overlapping contours) с оговоркой что нужно делать исправление таких шрифтов прежде чем их выводить на принтеры без соответствующей поддержки.
К счастью, подобные дефектные глифы встречаются редко и только в мало известных шрифтах (и почему, спрашивается?). Считать такой дизайн некорректным позволяет простое соображение — дизайнер не задумываясь ограничивает набор алгоритмов, пригодных для растеризации его глифа. Имеется в виду, что использовать аглоритм even-odd для растеризации становится невозможно, только более затратный nonzero.
Не смотря на принятые в библиотеке меры по борьбе с контурными дефектами, вероятность неудачной триангуляции сохраняется и равна 0.1% на наборе шрифтов Windows 7. Из 497931 глифов не получается преобразовать в сетку 680 глифов из следующего набора базовой плоскости UNICODE:
Basic Latin — 14 errors
Latin-1 Supplement — 9 errors
Latin Extended-A — 2 errors
Greek and Coptic — 2 errors
Thai — 11 errors
Letterlike Symbols — 1 errors
Mathematical Operators — 1 errors
Block Elements — 1 errors
Geometric Shapes — 1 errors
Hiragana — 1 errors
Enclosed CJK Letters and Months — 1 errors
CJK Unified Ideographs Extension A — 74 errors
CJK Unified Ideographs — 555 errors
Private Use Area — 3 errors
CJK Compatibility Ideographs — 4 errors
Если не брать в расчёт иероглифическое и тайское письмо, то всего 36 неудач из 497931 глифов (меньше 0.01%). В группе "Basic Latin", наблюдаются контурные дефекты следующих шрифтов: IrisUPC, KodchiangUPC, LilyUPC, Footlight MT Light, Kunstler Script, Papyrus, Parchment и Viner Hand ITC. По не странному совпадению большинство ошибок кроется в шрифтах UPC (Unity Progress Company).
Не смотря на обозначенные неудачи, прогноз в целом утешительный. Делается расчёт на более устойчивые варианты триангуляции, полная победа выглядит достижимой.
Определение контурной иерархии
Под иерархией подразумевается взаимоотношения контуров между собой. Символ "B", например, имеет 3 контура: один внешний и два контура-отверстия внутри него. Символ "Ы" имеет два независимых внешних контура и 1 внутренний контур-отверстие. Независимый контур с включенными в него контурами-отверстиями составляет один объект триангуляции. На следующей анимации изображён пример последовательной триангуляции нескольких контурных объектов в составе одного глифа.
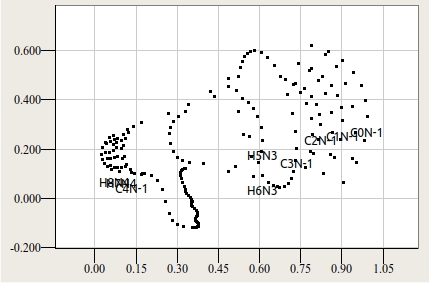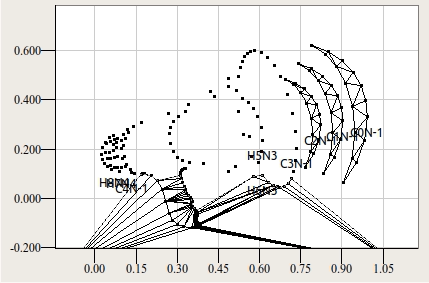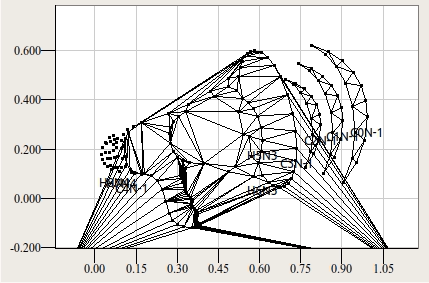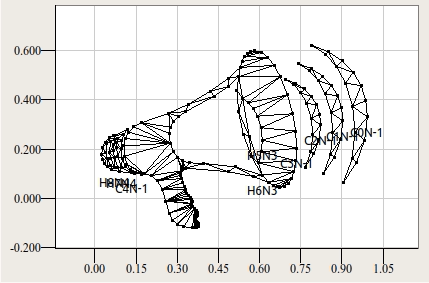
Такая мера вводится, в частности, для для борьбы с неудачной триангуляцией пересекающихся контуров. На рисунке ниже приводится два варианта дизайна символа U+00A2 — корректный (а), по моему мнению, и не корректный (б).
а)  б)
б) 
Первый вариант способен успешно триангулироваться. Второй — обречён на провал, поскольку одной сеткой два пересекающихся объекта представить невозможно без решения задачи контурного объединения. Контурное объединение предполагает поиск точек пересечения двух контуров… Весьма затратная операция. Вместо этого, оба приведённых контура триангулируются по отдельности. Результат — одна сетка включающая подсетки для "/" и для "C". Такой сеточный символ будет отображаться хорошо только при выключенном тесте глубины. Это своего рода компромисс — библиотека готова к произволу, но жертвовать производительностью из-за "ленивого" дизайна не будет.
Выпуклая триангуляция
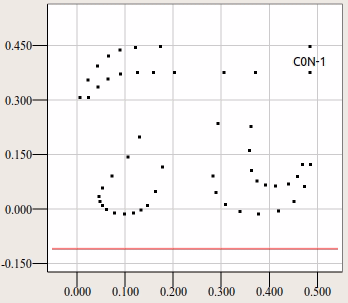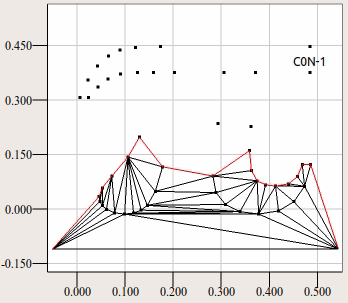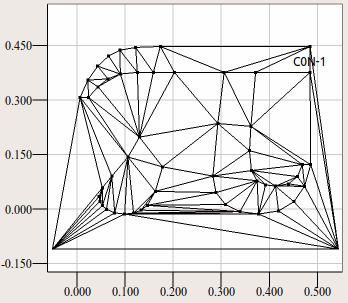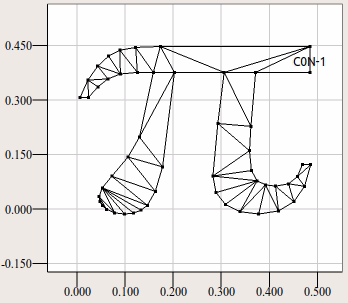
По предыдущим анимациям, думаю, становится ясен процесс подготовки сетки. На первом этапе делается выпуклая триангуляция без ограничений. То есть в триангуляции участвуют только точки. Кратко опишу алгоритм по следующей анимации.
1) Перебираются точки триангуляции ранее отсортированные по координате (y). Первая точка p19, потом p15 и так далее.
2) Из каждой точки опускается вертикаль на заметающую ломаную. Эта вертикаль пересекает в составе ломаной определённый отрезок. Заметающая ломаная, она же advancing front, изображена красным. На текущем шаге вертикаль вниз опускается из выделенной жирным точки. Находится отрезок под этой точкой.
3) Найденный таким образом отрезок и текущая точка составляют новый треугольник, после чего найденный отрезок исключается из заметающей ломаной, а заместо него вставляется 2 образовавшихся ребра треугольника. Если вертикаль опустилась точно по границе двух отрезков, то строится два треугольника.
4) Если после п.3 в составе ломаной образовалась остроугольная впадина из двух соседствующих отрезков, то на них строится новый треугольник. Отдельно показано после обработки вершины p2.
5) После перебора всех точек триангуляция достраивается до выпуклой. При этом строятся треугольники на всех соседствующих отрезках, образующих впадину. Отдельно показано после обработки вершины p5.
Данный алгоритм имеет близкое соответствие (в части Point event) тому, что был предложен в 2008 году авторами V. Domiter & B. Zalik в их публикации "Sweep?line algorithm for constrained Delaunay triangulation" (DOI: 10.1080/13658810701492241).
Замечательная особенность этого алгоритма заключается (помимо выраженной линейности в нашем применении) в том, что производится сетка уже достаточно приближенная к оптимальной. Хотя, конечно, такой она не является. После триангуляции требуется провести оптимизацию для соответствия критерию Делоне.
По поводу вычислительной сложности. На следующем рисунке приводится экспериментально полученный график, демонстрирующий линейную сложность вычислительного процесса.
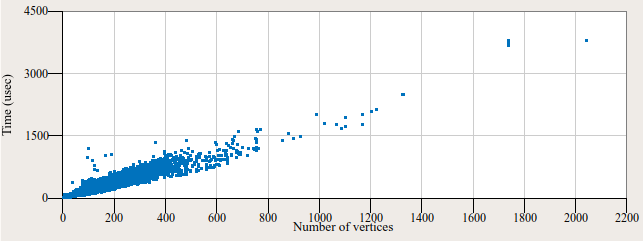
Каждая точка на плоскости определяет зависимость процессорного времени от числа вершин при конвертировании одиночного глифа (по оси X — число входных вершин, по Y — время их обработки в микросекундах).
Видно, что точки хорошо приближаются прямой, что говорит о сложности всего вычислительного процесса (и процесса триангуляции в частности) близкой к O(N). Конечно, в алгоритме присутствует сортировка вершин со сложностью O(N log N) и ещё несколько нелинейных вычислений, но они требуют значительно меньше времени процессора, нежели чем алгоритм триангуляции. Поэтому на приведённом графике их вклад фактически не прослеживается.
На верхнем графике замечено, что среди всех глифов есть рекордсмен, контуры которого содержат в сумме более 2000 вершин. Представитель шрифта "Tibetan Machine Uni" с именем U+0FC7 (Tibetan Symbol Rdo Rje Rgya Gram) выигрывает всеобщее внимание:
После триангуляции:
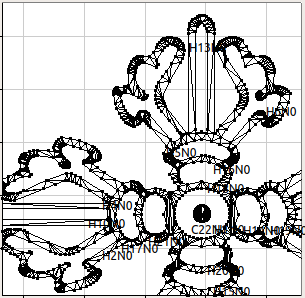
Вывод OpenGL с MSAA:

Так и вижу рыдающего ребёнка на уроке каллиграфии...
Продолжение следует
Уже сейчас статья получилась достаточно объёмной. Поэтому по другим пунктам (добавление ограничений, удаление лишних треугольников, оптимизация Делоне и формирование сетки) продолжу в следующей статье. Кроме того, эксперименты продолжаются и сохраняется несколько вопросов о наиболее выгодных способах обработки. По ним предстоит прийти к окончательному выводу.
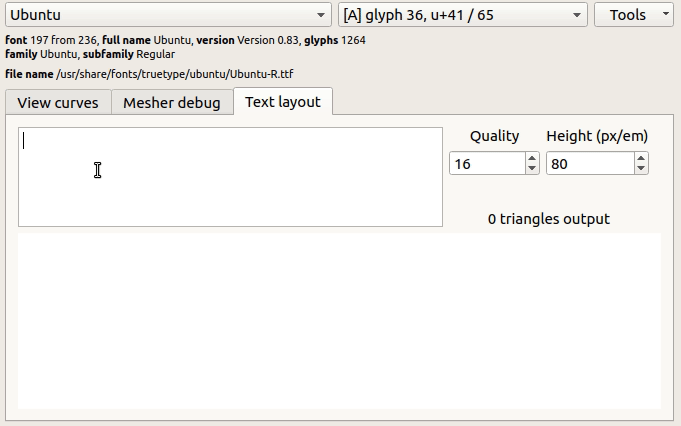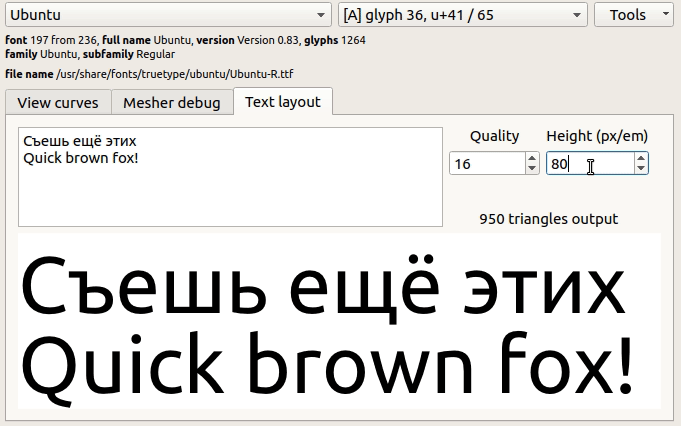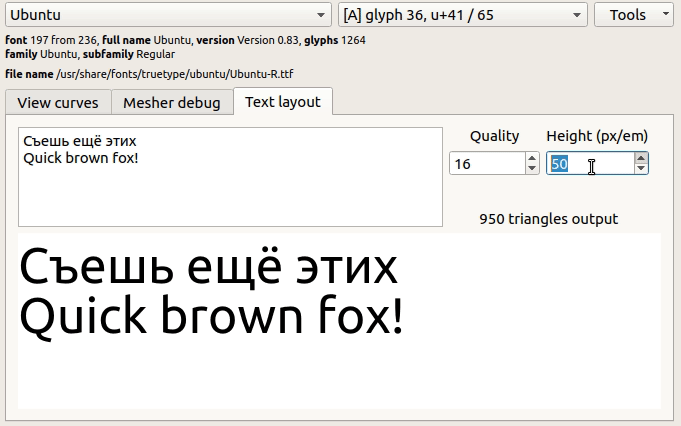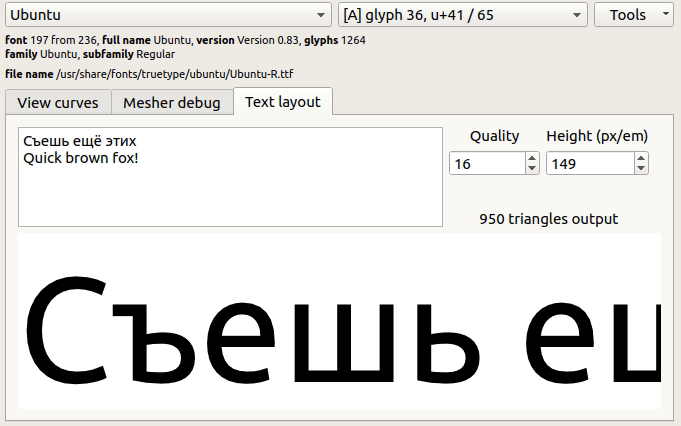
Дальнейшее развитие ttf2mesh заключается в оптимизации, расширении поддержки на другие форматы шрифтов. Будет создана коллекция OBJ файлов разных шрифтов. Отдельно предстоит организовать текстовые слои с экспортом текста в сеточный формат, SVG и, возможно, в PostScript.
Разработка будет вестись по мере свободного времени в остатке. Если появятся варианты капитализировать работу или пойдут донаты — то быстрее, конечно.
Библиотека ttf2mesh имеет MIT-лицензию и доступна по ссылке. Надеюсь, что она окажется общественно полезной.


psycha0s
При рендеринге векторных шрифтов крайне важно, насколько хорошо выглядит текст маленького размера. TTF файлы содержат специальные инструкции для выравнивания контура глифов маленького размера по пиксельной сетке (хинтинг). Учитывает ли ваша библиотека этот момент и может ли она подойти для рендеринга надписей в GUI или текта в браузере?
fse Автор
Здравствуйте. Вы абсолютно правы касательно хинтинга, это полезная технология для повышения в первую очередь отчётливости шрифта малого размера. К сожалению, вывод сеточного шрифта будет страдать тем же, чем и вывод обычной векторной графики — мелкоразмерные символы будут размываться.
В последней анимации видно, что текст читабелен при высоте символа меньше 6 пикселей, однако размывание контуров, несомненно, выше чем у хинтового вывода.
Сама scalable-технология едва ли допускает хинтинг. Но возможно ли применение хинтов в частном случае (ортогональная проекция с определённым масштабом) — над этим попробую подумать.
Для GUI и браузера сеточные шрифты потенциально подходят, хотя первичное применение представлялось другим. Опять же, с оговоркой, что отчётливось мелких символов теряется быстрее, чем у шрифтов с хинтом. На сколько это критично сегодня с учётом высоких дисплейных разрешений — надо исследовать.